6 класс 11.11.20 Теория. Алгебраическая сумма. Расстояние между точками. . Ссылка на видеоурок https://youtu.be/8pZGlur1i3U

16.11.2020г.

Математика

6 а/б класс. Ссылка на видеоурок https://youtu.be/8pZGlur1i3U

Тема урока: Алгебраическая сумма и ее свойства. Расстояние между точками координатной прямой. Правило вычисления значения алгебраической суммы двух чисел. Нахождение алгебраической суммы целых чисел. Нахождение расстояния между точками координатной прямой.

Открой тетрадь и запиши число на полях и «Классная работа».

Ниже запиши тему урока.

Сегодня мы поговорим о понятии алгебраическая сумма, сформулируем правила вычисления значений алгебраической суммы. Рассмотрим, как находить расстояние между точками координатной прямой. Потренируемся находить значение алгебраической суммы, а также будем находить расстояние между точками, если известны ее координаты.

Самые важные моменты теории необходимо законспектировать себе в тетрадь!

Понятие алгебраической суммы

Рассмотрим выражения +4 - 6 и -6 + 4, как перемещение точки по координатной прямой от начала отсчета. В первом выражении точка от начала координат переместилась сначала на 4 единичных отрезка вправо, потом на 6 единичных отрезков влево, во втором от начала координат на 6 единичных отрезков влево, а потом на 4 вправо. Понятно, что порядок перемещения точки на конечное положение ее не влияет.

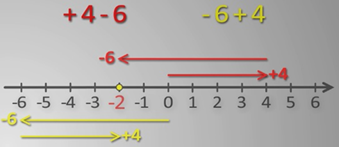
Рассмотрим данные выражения как описание финансовой деятельности. В обоих выражениях отражены доходы и расходы. В первом выражении предприятие получило прибыль +4, при этом расходы составили -6. Во втором выражении расходы составили -6, а прибыль +4. В конечном итоге результат одинаковый убытки -2.

Выражения, содержащие числа, знаки + и -, можно представить в виде суммы положительных и отрицательных чисел. Например, +4 - 6 можно представить в виде суммы (+4) + (-6). Такие выражения называют алгебраическими суммами.

Каждое слагаемое алгебраической суммы представляет собой число вместе с тем знаком, который стоит (или подразумевается, что стоит) перед ним, а законы арифметических действий применяются именно к этим слагаемым. Другими словами, алгебраическая сумма – это выражение, которое можно представить в виде суммы положительных и отрицательных чисел.

Свойства алгебраической суммы

Перейдем к свойствам алгебраических сумм. Рассмотрим выражения (+9) + (-5) и (-5) + (+9). Данные выражения отличаются друг от друга тем, что слагаемые в них стоят в обратном порядке. Найдем значения выражений любым способом, например,с помощью координатной прямой. Результаты данных выражений равны минус 1. Следовательно, при сложении чисел с любыми знаками переместительный закон справедлив: от перстановки слагаемых значение суммы не изменяется.

Представим выражение 34 -25 – 5 в виде суммы положительных и отрицательных чисел:

(+34)+(-25)+(-5). Удобнее найти значение данного выражения, если вначале сложить отрицательные числа, а потом положительное прибавить, можно выполнять действия и по порядку. Значение выражения при этом не изменится? В обоих случаях будет равно 4. Следовательно, для алгебраической суммы чисел справедлив и сочетательный закон: сумма не изменится, если какую-либо группу рядом стоящих слагаемых заменить их суммой.

Выполним практическое задание. Найдем значения выражения –(-56) + (-18) – 21.

Вспомним –(-а) = а. Преобразуем выражение: –(-56) = 56, поличится 56 + (-18) -21, представим выражение алгебраической суммой (+56) + (-18) + (-21). Найдем значение любым способом. Получится +17.

Теперь немного отдохни и сделай физ.минутку.

Раз – подняться, подтянуться,

Два – согнуться, разогнуться,

Три – в ладоши три хлопка,

Головою три кивка.

На четыре – руки шире.

Пять – руками помахать,

Шесть – успокоиться и сесть.

Повтори еще 2 раза. Можешь продолжить обучение.

Теперь поговорим о том как найти расстояние между точками, если известны ее координаты.

Правило нахождения расстояния между точками координатной прямой

В этом уроке выведем правило нахождения расстояния между точками координатной прямой, а также научимся находить длину отрезка, используя это правило.

Выполним задание:

Сравните выражения

при

1. а = 9, b = 5;

2. а = 9, b = -5;

3. а = -9, b = 5;

4. а = -9, b = -5.

Подставим значения в выражения и найдем результат:

Модуль разности 9 и 5 равен модулю 4, модуль 4 равен 4. Модуль разности 5 и 9 равен модулю минус 4, модуль -4 равен 4.

Модуль разности 9 и -5 равен модулю 14, модуль 14 равен 14. Модуль разности минус 5 и 9 равен модулю -14, модуль -14=14.

Модуль разности минус 9 и 5 равен модулю минус 14, модуль минус 14 равен 14. Модуль разности 5 и минус 9 равен модулю 14, модуль 14 равен 14

Модуль разности минус 9 и минус 5 равен модулю минус 4,модуль -4 равен 4. Модуль разности минус 5 и минус 9 равен модулю 4, модуль 4 равен (l-9 – (-5)l = l-4l = 4; l-5 – (-9)l = l4l = 4)

В каждом случае получились равные результаты, следовательно, можно сделать вывод:

Значения выражений модуль разности а и b и модуль разности b и а равны при любых значениях a и b.

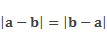
Еще одно задание:

Найдите расстояние между точками координатной прямой

1.А(9) и В(5)

2.А(9) и В(-5)

На координатной прямой отметим точки А(9) и В(5).

Сосчитаем количество единичных отрезков между данными точками. Их 4, значит расстояние между точками А и В равно 4. Аналогично найдем расстояние между двумя другими точками. Отметим на координатной прямой точки А(9) и В(-5), определим по координатной прямой расстояние между этими точками, расстояние равно 14.

Сравним результаты с предыдущими заданиями.

Модуль разности 9 и 5 равен 4, и расстояние между точками с координатами 9 и 5 тоже равно 4. Модуль разности 9 и минус 5 равен 14, расстояние между точками с координатами 9 и минус 5 равно 14.

Напрашивается вывод:

Расстояние между точками А(а) и В(b) координатной прямой равно модулю разности координат данных точек | a – b |.

Причем расстояние можно найти и как модуль разности b и а, так как количество единичных отрезков не изменится от того, от какой точки мы их считаем.

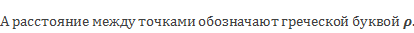
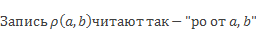
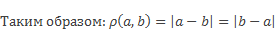
Правило нахождения длины отрезка по координатам двух точек

Найдем длину отрезка CD, если на координатной прямой С(16), D(8).

Мы знаем, что длина отрезка равна расстоянию от одного конца отрезка до другого, т.е. от точки С до точки D на координатной прямой.

Воспользуемся правилом:

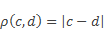
и найдем модуль разности координат с и d

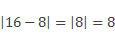
Итак, длина отрезка CD равна 8.

Рассмотрим еще один случай:

Найдем длину отрезка MN, координаты которого имеют разные знаки М (20), N (-23).

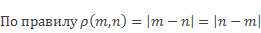
Подставим значения

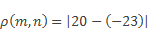
мы знаем, что –(-23) = +23

значит, модуль разности 20 и минус 23 равен модулю суммы 20 и 23

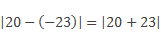
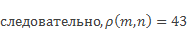
Найдем сумму модулей координат данного отрезка:

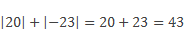
Значение модуля разности координат и сумма модулей координат в данном случае получились одинаковыми.

Можно сделать вывод:

Если координаты двух точек имеют разные знаки, то расстояние между точками равно сумме модулей координат.

На уроке мы познакомились с понятием алгебраическая сумма, с правилами ее вычисления. Также рассмотрели правило нахождения расстояния между двумя точками координатной прямой и научились находить длину отрезка, используя данное правило.