Теория массового обслуживания (ТМО) представляет собой прикладную математическую дисциплину, занимающуюся исследованием показателей производительности технических устройств, или, как мы будем говорить, систем массового обслуживания (СМО), предназначенных для обработки поступающих в них заявок на обслуживание, или требований. При этом существенную роль играют случайные отклонения в процессе поступления и обслуживания заявок.
Стимулом к развитию теории массового обслуживания послужили попытки предсказывать случайно изменяющиеся потребности по результатам наблюдений и на основе этого организовывать обслуживание, характеризующееся приемлемым временем ожидания.
Теория массового обслуживания позволяет раскрывать природу очередей, что обеспечивает возможность лучшего управления процессом. Например, потери покупателей магазине из-за медленного обслуживания у касс можно избежать, увеличив число кассиров, что снизит потери. Пожалуй, в этом деле можно обойтись без теории массового обслуживания. Но без нее не обойтись, например, при организации управления движением самолетов в аэропорту с максимальной слаженностью, вследствие большого числа действующих факторов и сложности системы. Эта теория позволяет прогнозировать длительность ожидания, число клиентов, ожидающих в какой-либо момент времени, длительность интервала занятости и т.д. Такого рода прогнозы помогают владельцу предприятия предвидеть ситуацию и принимать соответствующие меры для устранения перегрузки. Кроме того, теория побуждает как владельца предприятия, так и клиента осознавать постоянную необходимость в новых идеях для упрощения сложных проблем современной жизни. Теория массового обслуживания непосредственно не связана с оптимизацией. Она скорее пытается разработать, изучить и сравнить различные ситуации, характеризующиеся образованием очереди, и, таким образом, косвенно достигнуть приближенной оптимизации.
Просмотр содержимого документа
«АЛГОРИТМ РЕШЕНИЯ ЗАДАЧ СИСТЕМЫ МАССОВОГО ОБСЛУЖИВАНИЯ. Одноканальная СМО с отказами.»
АЛГОРИТМ РЕШЕНИЯ ЗАДАЧ СИСТЕМЫ МАССОВОГО ОБСЛУЖИВАНИЯ Одноканальная СМО с отказами
Пусть СМО состоит только из одного канала (n=1) и на нее поступает пуассоновский поток заявок с интенсивностью λ, зависящей в общем случае от времени
λ = λ (t) (2.1).
Заявка, заставшая канал занятым, получает отказ и покидает систему. Обслуживание заявки продолжается в течение случайного времени Тоб , распределенного по показательному закону с параметром m
f(t)= me-mt (t0) (2.2)
Из этого следует, что «поток обслуживаний» - простейший, с интенсивностью μ. Требуется найти: абсолютную (А) и относительную (Q) пропускные способности.
Рассмотрим единственный канал обслуживания как физическую систему S, которая может находиться в одном из двух состояний: S0– свободен, S1 – занят. Обозначим вероятности состояний p0(t) и p1(t). Очевидно:
tp0(t)+p1(t)=1 (2.3)
 Граф состояний системы:
Граф состояний системы:
По графу состояний системы составим дифференциальные уравнения Колмогорова:
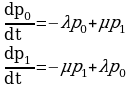 (2.4)
(2.4)
В соответствии с (2.3) одно уравнение (2.4.) лишнее. Отбросим второе уравнение, а первое перепишем с учетом (2.3):
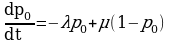 или
или 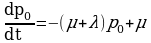 (2.5).
(2.5).
Это уравнение естественно решать при начальных условиях
p0(0)=1; p1(0)=0. Уравнение (2.5) легко может быть решено не только для простейшего потока заявок (λ =const), но и для случая λ = λ (t). Приведем решение (2.5) только для случаяλ =const:
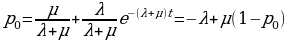

Для нашего случая вероятность p0 есть не что иное, как Q.
Действительно, p0 есть вероятность того, что в момент t канал свободен, иначе вероятность того, что заявка, пришедшая в момент t, будет обслужена. А значит, для данного момента времени t среднее число обслуженных заявок к числу поступивших также равно p0: Q= p0.
Когда процесс обслуживания уже установится, предельное значение Q будет равно:
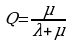 .
.
Легко найти и А, зная Q. Они связаны очевидным соотношением:
A=λQ.
А тоже установится и будет равна:
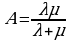 .
.
Зная Q (вероятность того, что пришедшая в момент t заявка будет обслужена) легко найти вероятность отказа: Pотк =1-Q. Pотк есть не что иное, как средняя доля необслуженных заявок среди поданных.
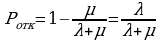 .
.







 Граф состояний системы:
Граф состояний системы: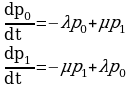 (2.4)
(2.4)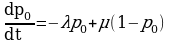 или
или 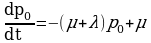 (2.5).
(2.5).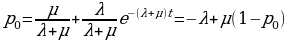

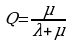 .
.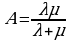 .
.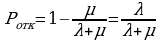 .
. 









