Индивидуальный итоговый проект "Звезды на ладони"

Муниципальное бюджетное общеобразовательное учреждение города

Новосибирск «Средняя общеобразовательная школа №158»

К ЗАЩИТЕ

Директор МБОУ СОШ №158

Т. В. Сундрунова

«___»_______20__г.

ИНДИВИДУАЛЬНЫЙ ИТОГОВЫЙ ПРОЕКТ

Предметная область: математика

Тема: Звезды на ладони

Исполнитель

Учащийся 9 «В» ___________________ (Э.А. Мохов)

(подпись, дата)

Руководитель ___________________ (Н.Я. Пономарева)

(подпись, дата)

Нормоконтроль пройден ___________________ (Н.В. Спирина)

(подпись, дата)

Новосибирск 2021

Содержание
				Стр.
Введение				2
Глава I.	Координаты. Системы координат			4
	1.1.	История возникновения системы координат		5
	1.2.	Виды систем координат		6
		1.2.1. Прямоугольная система координат на плоскости		6
		1.2.2. Другие системы координат		8
		1.2.3. Координаты в астрономии		9
Глава II.	Зодиакальные созвездия			12
	2.1.	История возникновения зодиакальных созвездий		14
	2.2.	Зодиакальные созвездия в астрологии		14
Глава III.	Практическая часть			17
	3.1.	Переход от полярной системы координат к декартовой		17
	3.2.	Построение графических изображений		17
	3.3.	Определение знаков зодиака одноклассников		26
Заключение				29
Список использованных источников				30

Введение

Никого не оставляет равнодушным наблюдение за звёздным небом. Интересно находить знакомые созвездия, но еще больше незнакомые группы звезд и рассматривать их, пытаясь разгадать тайну названия образованного созвездия. Помимо красивого расположения на небе, о созвездиях можно узнать уникальные, интереснейшие мифы и легенды, теории происхождения, названия и местоположения главных звёзд в знаках зодиака и многое другое. Поэтому мною принято решение познакомиться с созвездиями и непременно связать их расположение с координатной плоскостью, как бы "положить звезды на свою ладонь" и внимательно их рассмотреть, чтобы понять расположение звезд из любой другой, отдаленной на соответствующее расстояние от Земли, точки космического пространства.

Цель: Научиться пользоваться математическими знаниями при определении положения зодиакальных созвездий на карте звездного неба и при построении их графических изображений в прямоугольной системе координат

Объект исследования: математика

Предмет исследования: координатная плоскость

Данная тема актуальна, потому что показывает применение различных математических знаний в других науках, в частности, в астрономии, даст мне и моим одноклассникам стимул к более глубокому изучению математики, и она обязательно встретится нам в будущих профессиях.

Задачи:

1.Познакомиться с историей возникновения системы координат и зодиакальных созвездий .

2.Научиться видеть известные мне математические знания при изучении географической карты и карты звездного неба и попробовать осознанно их применить.

3. Научиться свободно ориентироваться на географической карте и карте звездного неба.

4. Изучить зодиакальные созвездия.

5.Построить изображение созвездий на координатной плоскости в программе GeoGebra.

6.Определить по дате рождения одноклассников принадлежность к знаку Зодиака; проанализировать результаты и определить их количественное соотношение.

7.Подготовить материал для выступления.

8.Создать презентацию по результатам исследования.

Гипотеза: Математические знания, получаемые в школе, применимы в других областях знаний.

Практическая значимость:  Без знания математики изучение других предметных дисциплин было бы невозможно.

Методы исследования:

• изучение информации по данной теме по разным источникам, её анализ:

-интернет

-литература

• обобщение и анализ результатов, полученных в результате определения названий зодиакальных созвездий по датам рождения одноклассников.

• Графическое моделирование.

Глава I. Координаты. Системы координат

Рассмотрим определение слова координата в различных источниках.

Из Иллюстрированного энциклопедического словаря Ф.А.Брокгауза и И.А.Эфрона [1] узнаем, что:

Координаты. - 1) Геом., величины , определяющие положение точки на плоскости и в пространстве; на плоскости положение точки чаще всего определяется расстояниями (перпендикулярами) от двух прямых, пересекающихся в одной точке по прямым углом (началом координат); одна из координат называется ординатой, а другая - абсциссой. - В пространстве по системе Декарта положение точки определяется относительно трех плоскостей координат, пересекающихся в одной точке, или сферическими координатами, начало координат находится в центре сферы. - 2)Астрон., величины при помощи которых определяется положение звезды, например, прямое восхождение и склонение.-3) Географ., широта, долгота и высота над известным общим уровнем (например, океана).

А Военно-морской словарь. Гл.ред. В.Н.Чернавин [2] даёт следующее определение:

Координаты ( от лат. со - совместно и ordinatus - упорядоченный, определенный), совокупность угловых или линейных величин, определяющих положение точки на любой поверхности или в пространстве.

Астрономические координаты: угловые величины, названные астрономической широтой (фи) и долготой (лямбли), определяющие положение точки на земной поверхности относительно экватора и начального астрономического (Гринвич) меридиана, полученные из наблюдений небес, светил. Расхождения между астрономическими и географическими координатами малы и при решении некоторых задач (например в морской навигации) отождествляются.

1.1. История возникновения системы координат

С древнейших времен начинается история возникновения координат и системы координат. Идея использования координат первоначально возникла ещё в древнем мире в связи с потребностями астрономии, географии, живописи.

Составителем первой географической карты считают древнегреческого ученого Анаксимандра Милетского (ок. 610-546 до н.э.). Используя прямоугольные проекции, он четко описывал широту и долготу места.

К оме него, более чем за 100 лет до н.э. греческий ученый Гиппарх (Рис.1(слева, держит звездный глобус) предложил опоясать на карте земной шар параллелями и меридианами и ввести теперь хорошо известные географические координаты: широту и долготу и обозначить их числами.

Рис.1

Французскому математику Рене Декарту (Рис.2 ) принадлежит о сновная заслуга в создании современного метода координат. История, подтолкнувшая его к этому открытию, дошла до наших времён. Занимая в театре места, согласно купленным билетам, мы даже не подозреваем, кто и когда предложил ставший обычным в нашей жизни метод нумерации кресел по рядам и местам. Оказывается, эта идея осенила знаменитого философа, математика и естествоиспытателя Рене Декарта– того самого, чьим именем названы прямоугольные

Рис.2 координаты. Посещая парижские театры, он не уставал удивляться путанице, вызываемой отсутствием элементарного порядка распределения публики в зрительном зале. Предложенная им система нумерации, в которой каждое место получало номер ряда и порядковый номер от края, сразу сняла все поводы для раздоров и произвела настоящий фурор в парижском высшем обществе.

В своей работе «Рассуждение о методе» в 1637 году Рене Декарт впервые сделал научное описание прямоугольной системы координат. Поэтому прямоугольную систему координат называют также — Декартова система координат.

" В XIV веке французский математик Н.Орсем ввел по аналогии с географическими, координаты на плоскости. Он предложил покрыть плоскость прямоугольной сеткой и назвать широтой и долготой то, что мы теперь называем абсциссой и ординатой.

Это нововведение оказалось чрезвычайно продуктивным. На его основе возник метод координат, связавший геометрию с алгеброй. Точка плоскости - геометрический объект - заменяется парой чисел (х;у), т.е. алгебраическим объектом".[6]

В 70-80 годах XVII в. немецким математиком Г. В. Лейбницем (Рис.3) были введены в употребление

Рис.3. термины «абсцисса» (от латинского слова, обозначающего "отсекаемый отрезок от оси иксов") и "ордината" (обозначающего "упорядоченный"). Им же введен термин "координаты". Координата точки указывает положение точки на плоскости. Первыми вошедшими в систематическое употребление координаты являются астрономическими и г еографическими. Более систематически координаты стали применяться к вопросам геометрии на плоскости в 17 веке. В XVIII веке координатный метод для трёхмерного пространства впервые применил Леонард Эйлер (Рис.4).

Рис.4

1.2. Виды систем координат

Положение любой точки в пространстве (в частности, на плоскости) может быть определено при помощи той или иной системы координат. Числа, определяющие положение точки, называются координатами этой точки.

1.2.1. Прямоугольная система координат на плоскости

Для того, чтобы указать координату точки на плоскости берутся две перпендикулярные прямые (обычно одну из них располагают горизонтально, а другую – вертикально) и вводят на каждой из них обычные координаты. Эти координаты согласованы между собой, Точка пересечения прямых О - это начало отсчета на каждой координатной прямой; единичный отрезок, как правило, один и тот же. На горизонтальной прямой положительное направление выбирается "слева направо", на вертикальной – "снизу вверх". Эти направления показывают стрелками. Точка пересечения прямых- точка О- называется началом координат. Эта буква выбрана не случайно, а по сходству написания с цифрой 0 или как первая буква латинского слова origo- начало. Сами координатные прямые называются осями координат.

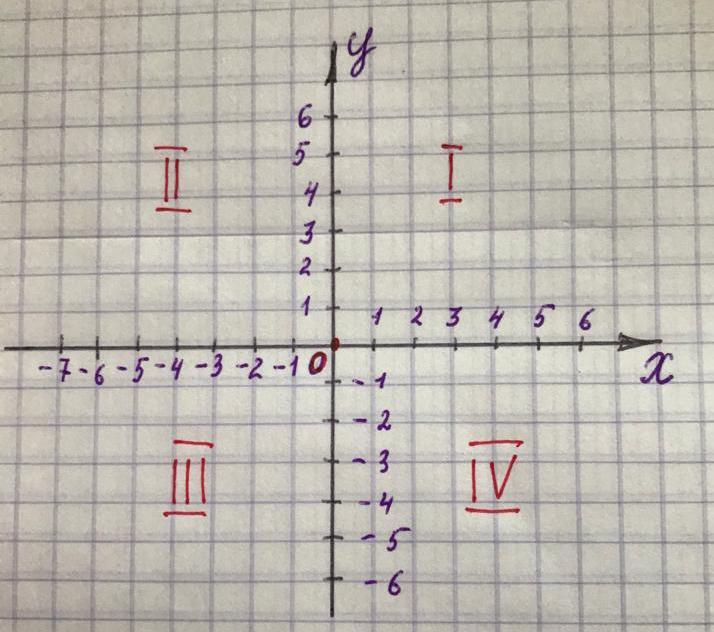
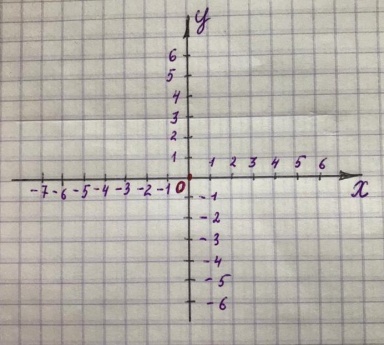
Рис.5. Координатная плоскость Рис.6. Координатные четверти

Горизонтальную ось называют осью абсцисс (осью Х), вертикальную ось называют осью ординат (или осью Y). Плоскость, на которой задана система координат, называется координатной плоскостью. (Рис.5)

Оси разбивают координатную плоскость на четыре области, которые называются координатными четвертями. Их нумеруют против часовой стрелки.(Рис.6).

Абсциссой точки М называется координата х=-2 точки на оси ОX, ординатой – координата у=4 точки М на оси ОY.

Координаты точки обычно указывают в скобках рядом с обозначением точки: М (-2;4). Между точками на плоскости и их координатами имеется взаимно однозначное соответствие.

1.2.2. Другие системы координат

Кроме изучаемых в школе прямоугольных систем координат, существует большое многообразие различных систем.

Название системы координат	Изображение
Географическая система координат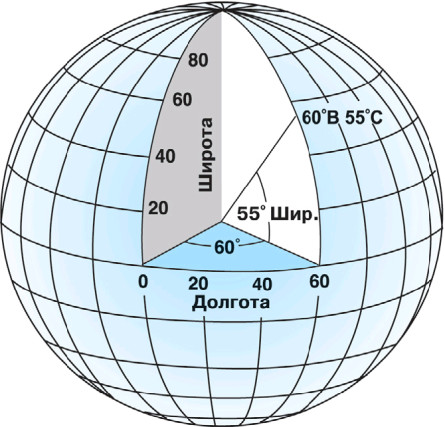
Полярная система координат
Цилиндрическая система координат
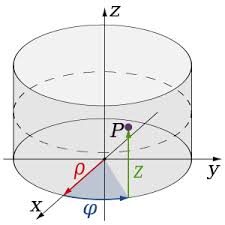
Сферическая система координат.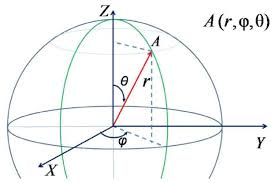
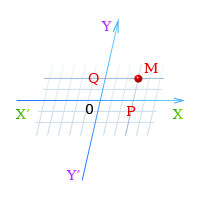
Косоугольная система координат.

1.2.3. Координаты в астрономии

Сложность в определении координат звезд состоит в том, что они движутся вместе с небесной сферой, но взаиморасположение звезд при этом не меняется. Созвездия неизменны вот уже многие столетия.

Чтобы сделать звездную карту, изображающую созвездия на плоскости, надо знать координаты звезд. Координаты звезд относительно горизонта, например, высота, хотя и наглядны, но непригодны для составления карт, так как всё время меняются. Система координат, которая вращается вместе со звездным небом называется экваториальной системой (Рис.7).

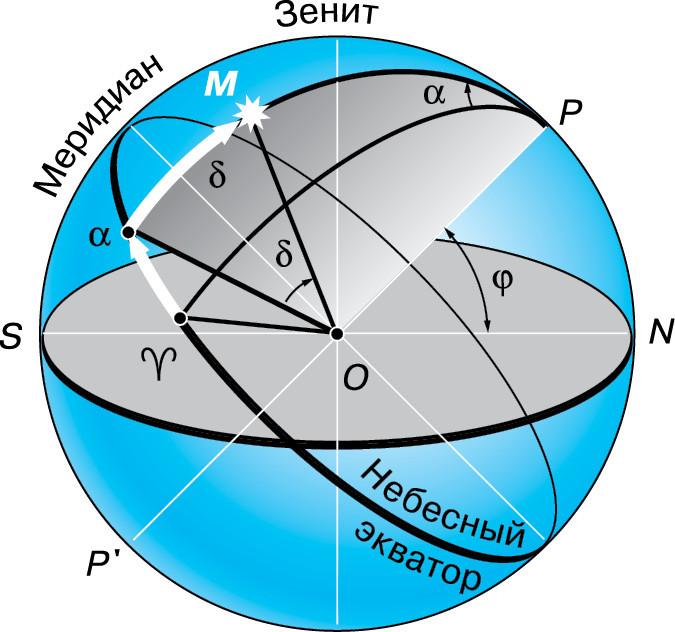
Рис. 7. Экваториальная система координат

В ней одной координатой является угловое расстояние светила от небесного экватора, называемое склонением 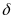. Оно меняется в пределах ±90° и считается положительным к северу от экватора и отрицательным — к югу. Склонение аналогично географической широте. Вторая координата аналогична географической долготе и называется прямым восхождением 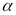. Прямое восхождение светила М измеряется углом между плоскостями большого круга, проведенного через полюсы мира и данное светило М, и большого круга, проходящего через полюсы мира и точку весеннего равноденствия. На одной карте можно изобразить без искажений только часть звездного неба, поэтому карта звездного неба представлена в виде двух полушарий: северное небо, южное небо и экваториального пояса (Рис.8). Экваториальные координаты звезд имеют большое практическое применение: по ним создают звездные карты и каталоги, определяют географические координаты пунктов земной поверхности, осуществляют ориентировку в космическом пространстве, проверяют время, изучают вращение Земли и т.д.

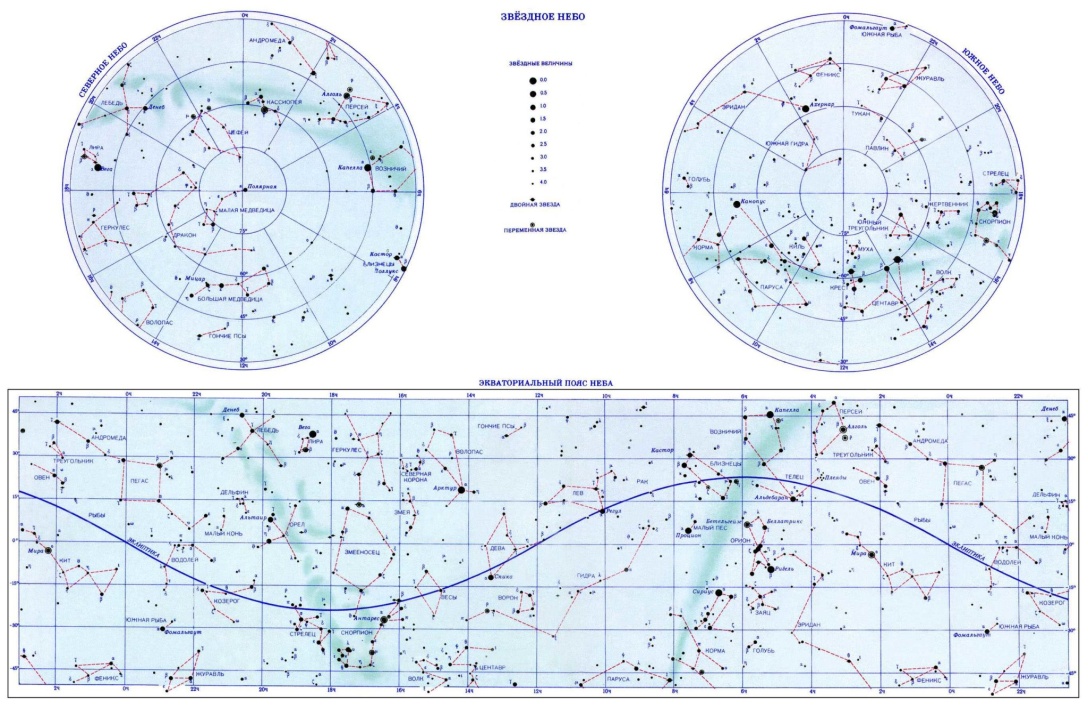
Рис.8

Глава II. Зодиакальные созвездия

Созвездия — в современной астрономии это участки, на которые разделена небесная сфера для удобства ориентирования на звёздном небе. В древности созвездиями назывались характерные фигуры, образуемые яркими звёздами. С древнейших времён люди видели некоторую систему во взаимном расположении звёзд и группировали их в соответствии с ней в созвездия.

В 1922 году на Международном астрономическом съезде (MAC) было принято, что число созвездий на всей небесной сфере составляет 88 (между которыми проведены строгие границы), из них 47 были присвоены имена примерно 4500 лет назад. Это Большая Медведица, Малая Медведица, Дракон, Волопас, Телец, Водолей и другие.

Значение слова СОЗВЕЗДИЯ узнаем из следующих источников:

- в словаре Ожегова

СОЗВЕЗДИЕ, -я, ср. 1. Один из 88 участков, на которые разделено звездное небо для удобства ориентировки и обозначения звезд (спец.); отдельная группа звезд.[3]

- в словаре Д.Н.Ушакова

СОЗВЕ́ЗДИЕ, созвездия, ср. (астр.). Группа звезд, условно объединенных общим названием. Двенадцать созвездий зодиака. [4]

- в словаре Энциклопедии

СОЗВЕЗДИЯ - участки звездного неба, выделенные для удобства ориентировки на небесной сфере и обозначения звезд. Все небо разделено на 88 созвездий, они носят имена мифических героев (напр., Геркулес, Персей), животных (Лев, Жираф), предметов (Весы, Лира) и др. Иногда в созвездия выделяют группу звезд с названием, отличным от названия созвездия, - астеризм (напр., Ковш в созвездии М. Медведицы). Наиболее яркие звезды в созвездии обозначены греческими буквами (обычно в порядке убывания яркости) с добавлением названия созвездия (напр., Возничего), менее яркие - латинскими буквами и цифрами. Границы созвездий проходят, как правило, вдоль небесных параллелей и кругов склонений. [5]

К зодиакальным относятся 13 созвездий: Овен, Телец, Близнецы, Рак, Лев, Дева, Весы, Скорпион, Змееносец, Стрелец, Козерог, Водолей, Рыбы. В астрологии же зодиакальными считаются только 12 – Змееносец в список не входит.

Причина, почему эти 13 созвездий такие особенные, очень проста – через них проходит эклиптика (Рис.9 Экваториальный пояс неба), то есть линия орбиты Земли вокруг Солнца. Когда Земля движется по орбите, совершая круг ровно за год, Солнце на небе движется как раз по линии эклиптики оказываясь на фоне разных созвездий.

Основа слова "зодиак" состоит из греческих слов "круг" и "животное". Перевод этого слова означает "круг животных", потому что 11 зодиакальных созвездий из 12 (исключение составляют Весы) носят названия живых существ: Телец, Овен, Рак, Лев, Дева, Скорпион, Близнецы, Козерог, Рыбы, Водолей, Стрелец. Видимое перемещение Солнца, Луны и планет происходит на фоне этих созвездий. Поэтому разные народы связывали Зодиак с образом "небесной дороги".

Созвездия Зодиака одни из самых древних. Их изображения археологи находят на многих памятниках, нередко вместе с изображениями Солнца, Луны и планет. Они встречаются на глиняных табличках, стенах гробниц, саркофагов, стелах, колоннах храмов. Фигурные изображения созвездий Зодиака служили и служат по сей день элементом ювелирных украшений и фасадов различных архитектурных сооружений.

2.1. История возникновения зодиакальных созвездий

Как показали исследования историков и археологов, именно астрономы античной Греции открыли годичное движение Солнца по небосводу, т. е. обнаружили ряд созвездий, через которые проходит эклиптика. Но ведь вид Солнца на небе не позволяет наблюдать звёзды, и наоборот, ночью на небе нет Солнца. Как же удалось узнать, какие созвездия оно проходит в течение года? Очень просто: всё началось с Луны. Не вызывает сомнения, что ещё в глубокой древности были выделены конфигурации звёзд, по которым совершает свой ежемесячный путь Луна. За год Земля делает один оборот вокруг Солнца. За это время Луна почти 12 раз проходит всю последовательность смены своих фаз, т. е. 12 раз в году бывает полнолуние, новолуние. Поэтому двенадцатимесячный год утвердился именно благодаря Луне, и пояс Зодиака разбит на 12 созвездий. Периодичность смены лунных фаз легла в основу календарей. Отсюда и слово «месяц» у нас означат и вид луны на небе, и интервал времени (28 – 31 день). Число 12 стало священным у разных народов. Двенадцать богов-олимпийцев у греков, римский император Диоклетиан объединил 12 провинций, Александр Македонский во время похода установил 12 жертвенников, в Индии колёса изготавливали с 12 спицами, герои и полубоги совершали 12 подвигов.

Впоследствии, подметив видимое движение Солнца, люди догадались, что оно перемещается на фоне тех же созвездий. Воображаемая линия годового движения Солнца называется эклиптикой. И планеты тоже, совершая свои перемещения по небу, пересекают созвездия Зодиака.

2.2.Зодиакальные созвездия в астрологии.

Не надо путать зодиакальные созвездия в астрологии и их же в астрономии. Если в астрономии они расположены строго в пределах своих границ, довольно извилистых и неравномерных, то в астрологии всё совсем по-другому.

Астрологические зодиакальные созвездия чисто условные – вся окружность эклиптики просто поделена на дуги по 30⁰, что даёт как раз 360⁰ за 12 месяцев. Каждой части присвоено одно из двенадцати зодиакальных созвездий – Змееносец выброшен из этого списка. Таким образом, в астрологии каждому месяцу присвоен один из астрологических знаков.

Всё это, конечно, чисто условно и ничего общего с реальным положением вещей не имеет. В астрономии, например, видно, что в созвездии Скорпиона на самом деле Солнце проводит всего 7 дней, а в астрологии ему также отводится месяц.

Поэтому знаки Зодиака из астрологии не имеют почти ничего общего с реальными зодиакальными созвездиями, кроме, разве что, названий. Астрологические символы этих созвездий в науке также не используются.

Глава III. Практическая часть

Построение изображения зодиакальных созвездий на координатной плоскости

3.1. Переход от полярной системы координат к декартовой

Знакомство с координатной плоскостью и вид звездного неба натолкнули меня на мысль, о переносе зодиакальных созвездий на координатную плоскость. Для этого необходимо перевести полярные координаты созвездий в декартовые. Если полюс полярной системы координат совместить с началом прямоугольной системы координат, а полярную ось с положительной полуосью OХ, то по известным полярным координатам точки А( ρ; φ) (Рис.9) её прямоугольные координаты вычисляются по формулам:

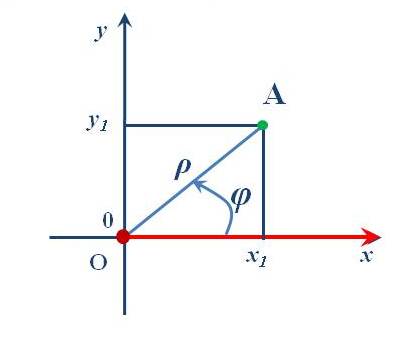x₁ = ρ cosφ, 

y₁ = ρ sinφ

Рис.9.

2.2.Построение графических изображений созвездий.

Для графического изображения созвездий я выбрал 12 зодиакальных созвездий.

На примере одной звезды (№1 условно названа) из созвездия Рак, я проиллюстрирую порядок нахождения координат звезд созвездия, используя карту звездного неба в полярной системе координат и формулы, приведенные на рисунке 9. На рисунке 10 показаны угол и расстояние  от начала координат до звезды № 1.

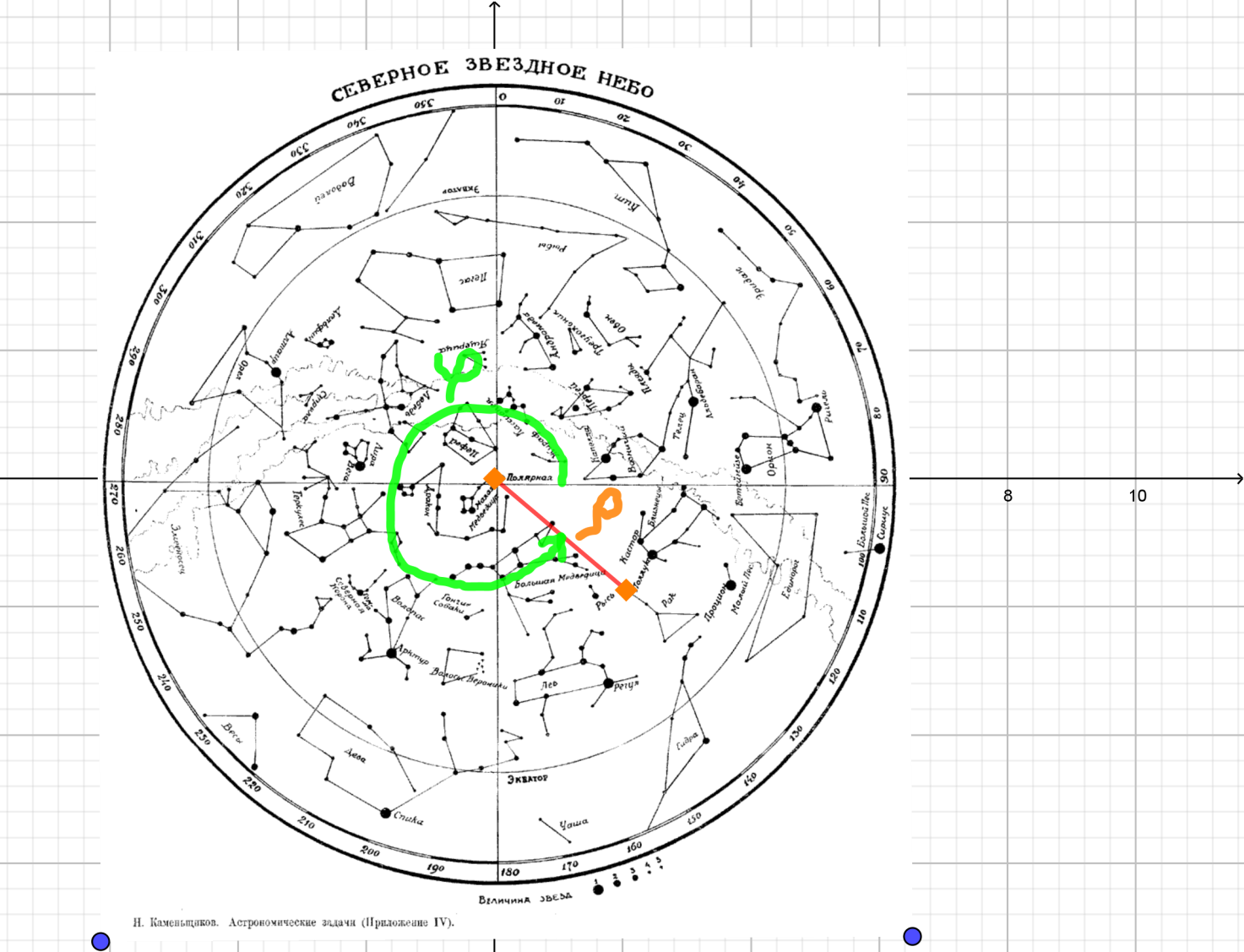
Рис.10

х = cosy = sin

Для звезды № 1:  см, 360°- 42°= 318°.

х = 9*cos 318° 9*0,74  6,68;

y = 9*sin 318° 9* (-0,68)  (-6, 02).

На координатной плоскости в программе GeoGebra отмечаем точку №1 с координатами (6,68; -6, 02) рис.11 .



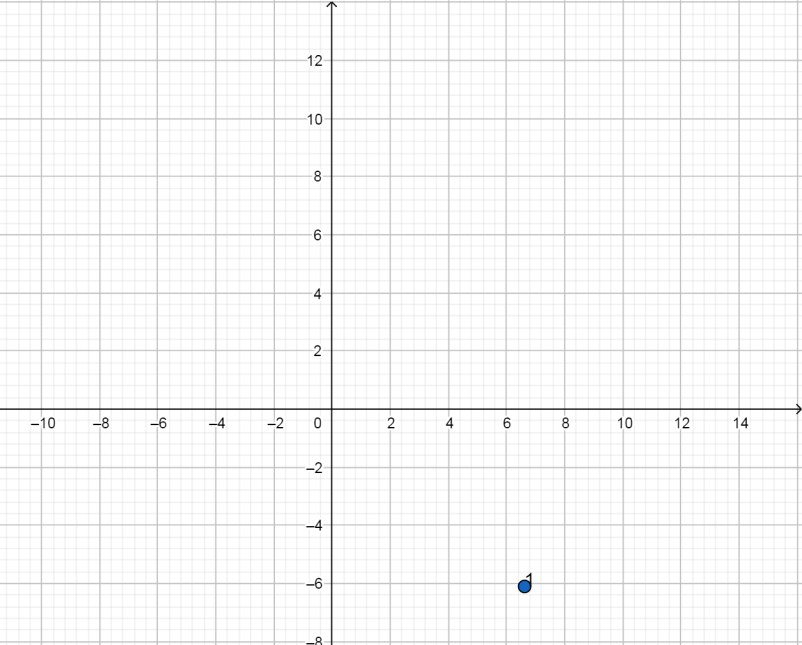
Рис.11

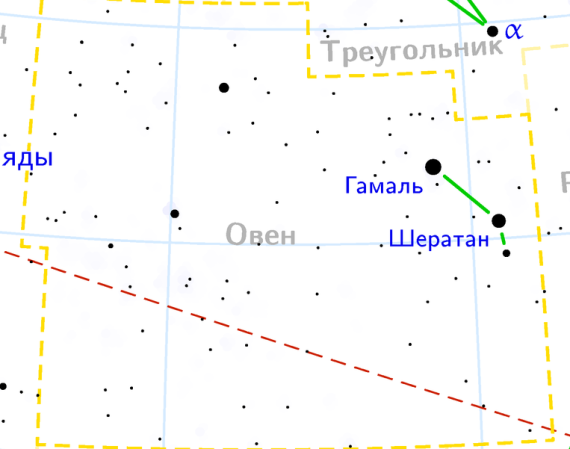
ОВЕН: 21 марта-20 апреля
Координаты
(4;4) (6;2) (6,5;1).
Графическое изображение созвездия	Изображение созвездия на карте звездного неба

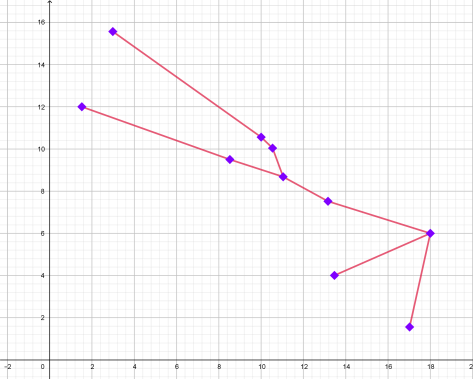
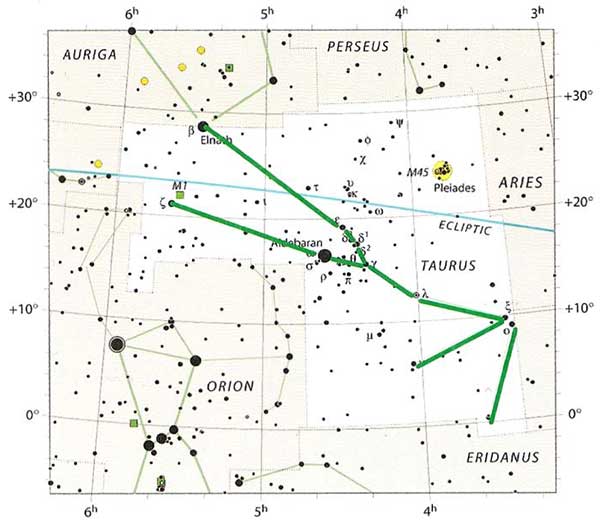
ТЕЛЕЦ: 21 апреля-21 мая
Координаты
1. (1,5; 12) (8,5; 9,5) (11; 8,75) 13,25; 7,5) (18; 6) (17; 1,5) 2. (11;8,75) (10,5; 10) (10; 10,5) ( 3; 15,5) 3. (18; 6) (13,54).
Графическое изображение созвездия	Изображение созвездия на карте звездного неба

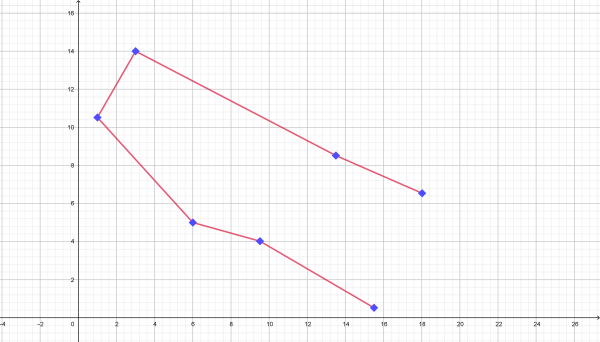
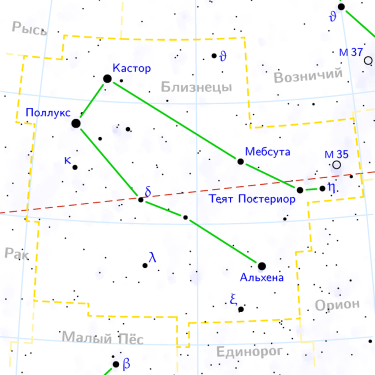
БЛИЗНЕЦЫ: 22 мая-21 июня
Координаты
(15,5; 0,5) (9,5; 4) (6; 5) (1; 10,5) (3;14) (13,5; 8,5) (18; 6,5).
Графическое изображение созвездия	Изображение созвездия на карте звездного неба

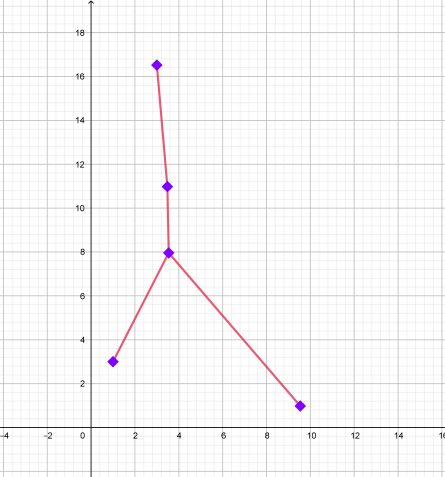
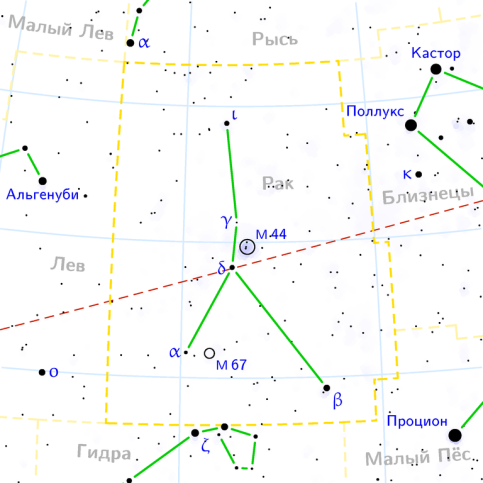
РАК: 22 июня-22 июля
Координаты
1. (1;3) (3,5; 8) (3,5; 11) (3; 16,5). 2. (3,5; 8) (9,5; 1).
Графическое изображение созвездия	Изображение созвездия на карте звездного неба

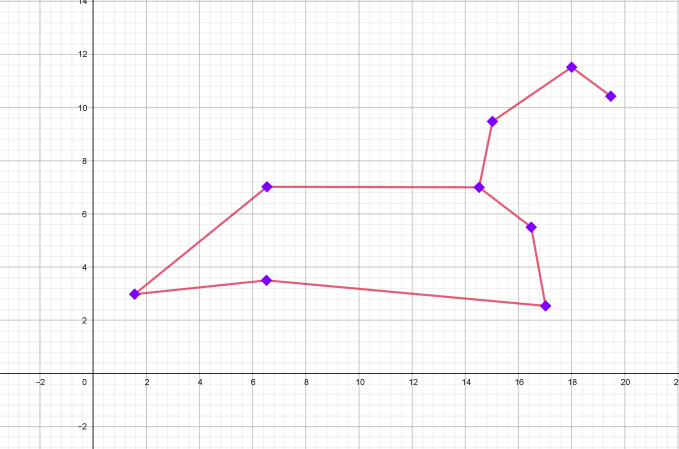
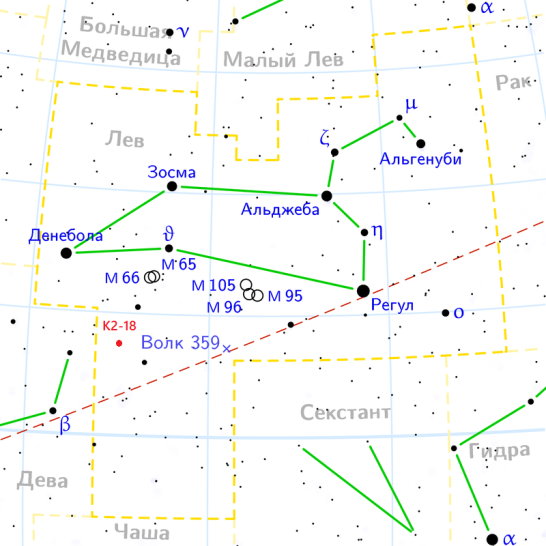
ЛЕВ: 23 июля-22 августа
Координаты
(19,5;10,5) (18; 11,5) (15; 9,5) (14,5; 7) (6,5; 7) (1,5; 3) (6,5; 3,5) (17; 2,5) (16,5; 5,5) (14,5; 7).
Графическое изображение созвездия	Изображение созвездия на карте звездного неба

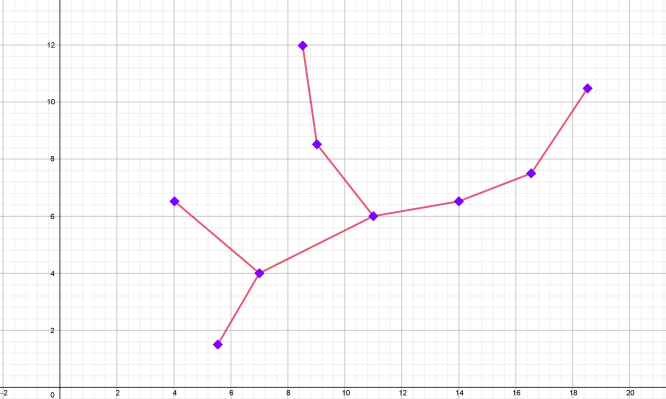
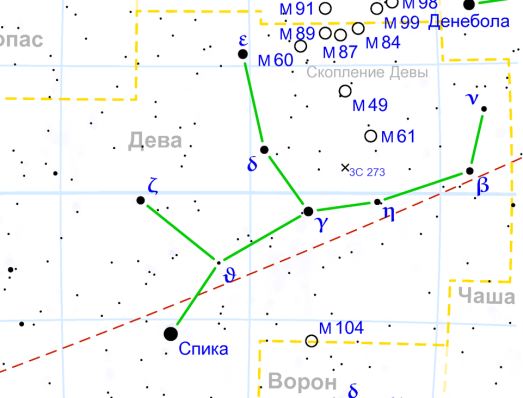
ДЕВА: 23 августа-22 сентября
Координаты
1. (5,5; 1,5) (7;4) (11;6) (14; 6,5) (17,5; 7,5) (18,54 10,5) 2. (7.4) (4; 6.5) 3. (11; 6) (9; 8,5) (8,5; 12).
Графическое изображение созвездия	Изображение созвездия на карте звездного неба

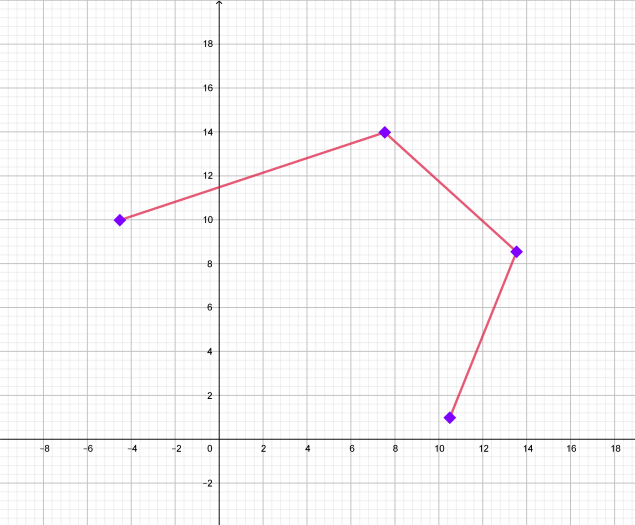
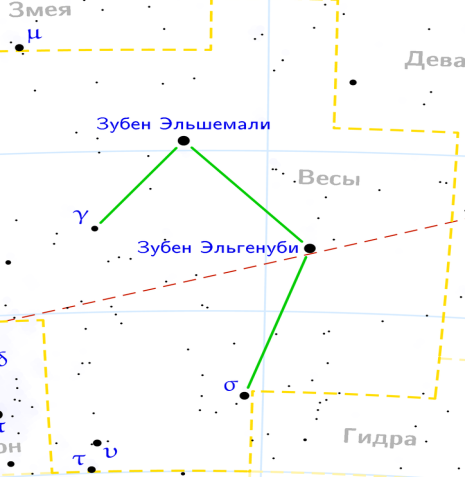
ВЕСЫ: 23 сентября-22 октября
Координаты
(-4,5; 10) (8,5; 14,5) (13,5; 8,5) (10,5; 1).
Графическое изображение созвездия	Изображение созвездия на карте звездного неба

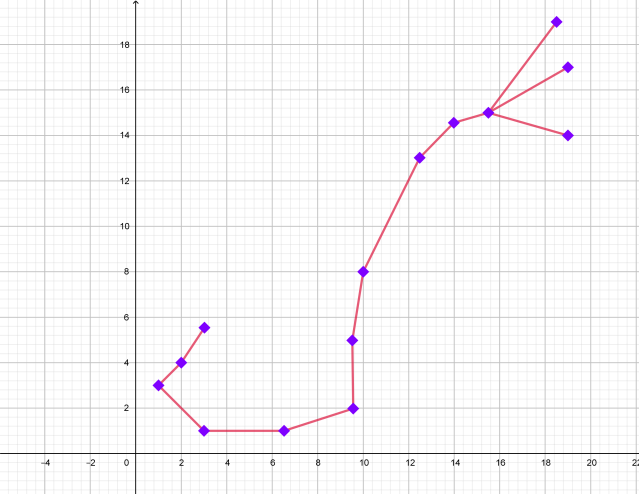
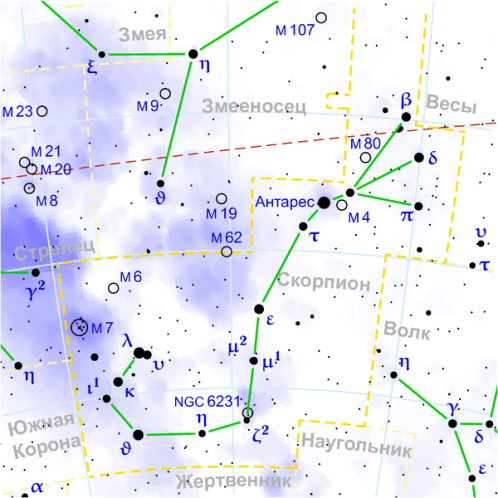
СКОРПИОН: 23 октября-22 ноября
Координаты
1. (3; 5,5) (2;4) (1;3) (3;1) (6.5; 1) (9,5; 2) (9,5; 5) (10; 8) (12,5; 13) (14; 14,5) (15,5; 15) (19;14). 2. (15,5; 15) (19; 17). 3. (15,5; 15) (18,5; 19).
Графическое изображение созвездия	Изображение созвездия на карте звездного неба

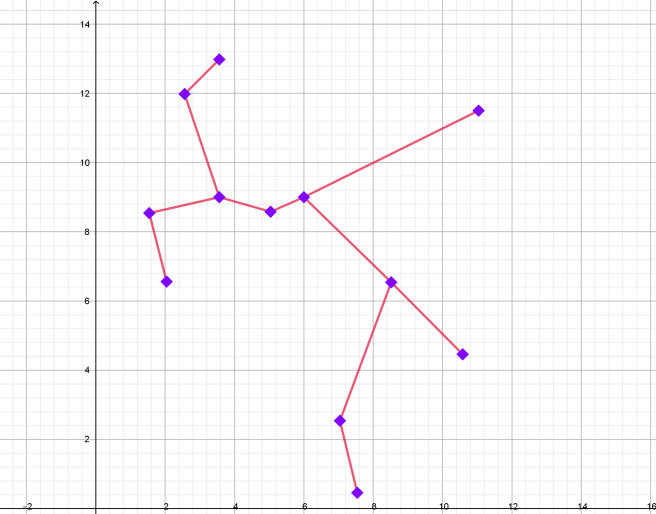
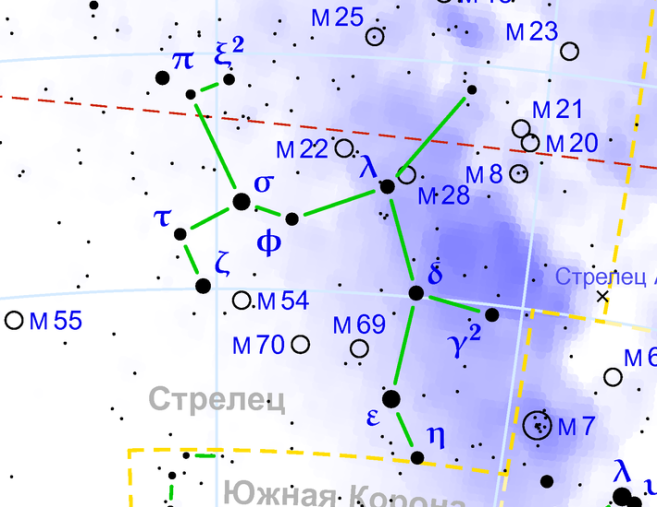
СТРЕЛЕЦ: 23 ноября-21 декабря
Координаты
1. (2; 6,5) (1,5; 8,5) (3,5; 9) (5; 8,5) (8;9) (8,5; 6,5) (7; 2,5) (7,5; 0,5) 2. (3,5; 9) (2,5; 12,5) (3,5; 13) 3. (8; 9) (11; 11,5) 4. (8,5; 6,5) (10,5; 4,5)
Графическое изображение созвездия	Изображение созвездия на карте звездного неба

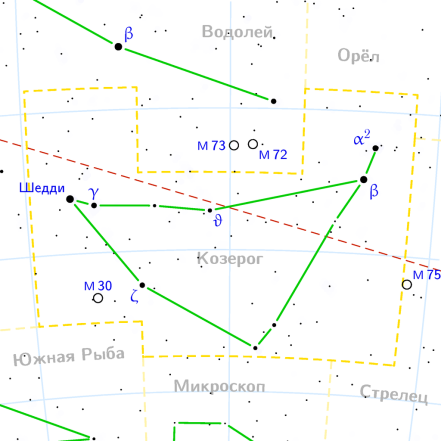
КОЗЕРОГ: 22 декабря-20 января
Координаты
(19,5; 8) (17,5; 6,5 ) (8; 9,5) (1,5 13,5) (0,5; 15) (1,5; 7,5) (6; 0,5) (7,5; 1) (17,5; 6,5).
Графическое изображение созвездия	Изображение созвездия на карте звездного неба

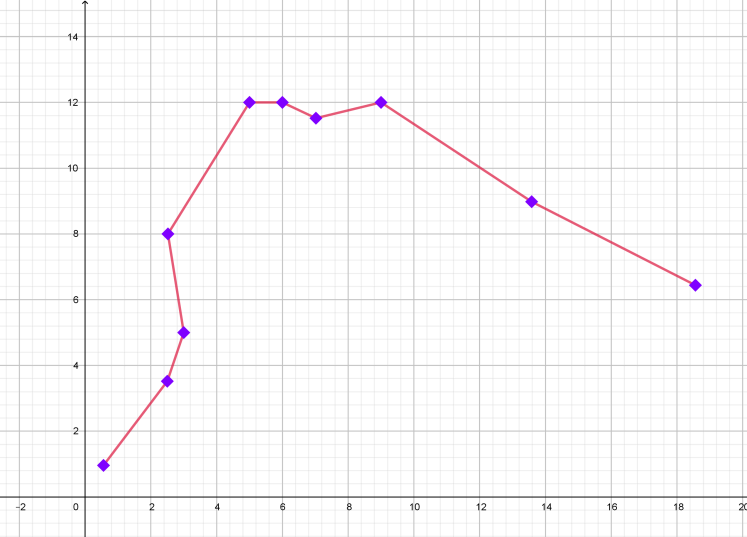
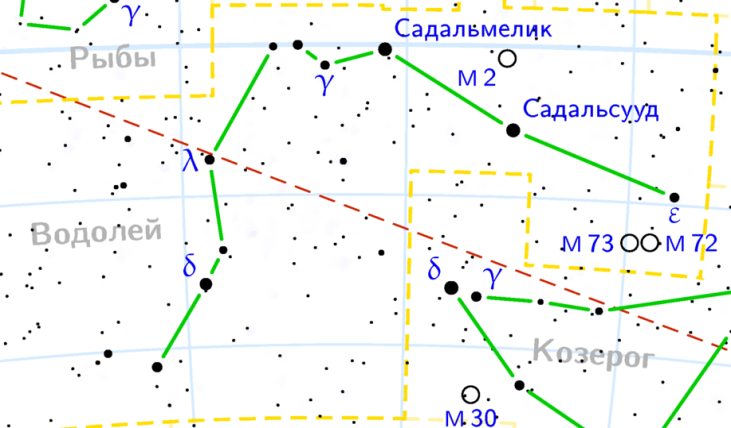
ВОДОЛЕЙ: 21 января-19 февраля
Координаты
(0,5; 1) (2,5; 3,5) (3; 5) (2,5; 8) (5; 12) (6; 12) (7; 11,5) (9; 12) (13,5; 9) (18,5; 6,5)
Графическое изображение созвездия	Изображение созвездия на карте звездного неба

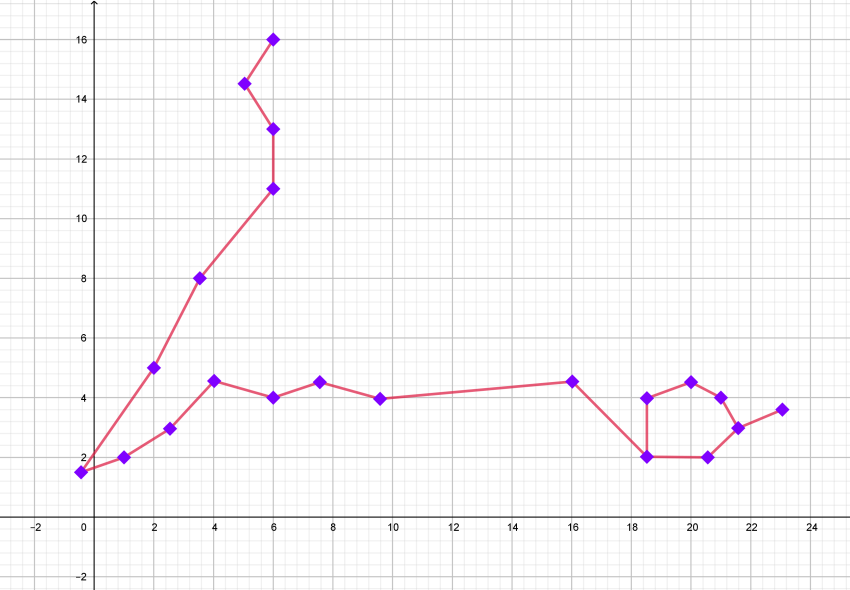
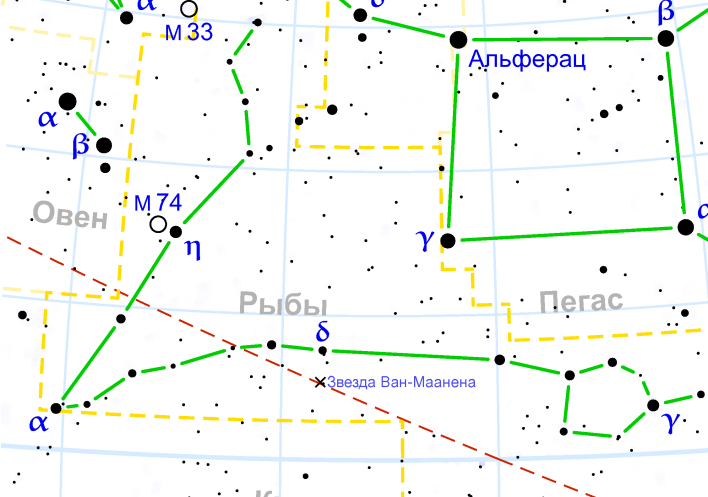
РЫБЫ: 20 февраля-20 марта
Координаты
(-0,5; 1,5) (2; 5) (3,5; 8) (6; 11) (6; 13) (5; 14,5) (6; 16). (-0,5; 1,5) (1; 2) (2,5; 3) (4; 4,5) (6;4) (7,5 4,5) (9,5; 4) (16; 4,5) (18,5; 2 ) (20,5) (21,5; 3) (23; 3,5). (18,5; 2) (18,5; 4) (20; 4,5) (21;4) (21,5;3).
Графическое изображение созвездия	Изображение созвездия на карте звездного неба

2.3. Определение знаков Зодиака по дате рождения одноклассников

По дате рождения одноклассников (Таблица № 1) я установил их знак Зодиака

Таблица № 1

№ пп	Имя, фамилия	День и месяц рождения	Знак зодиака
1	Артем М.	17.04	Овен
2	УльянаГ.	07.05	Телец
3	Ирина К	28.04	Телец
4	Иван Н.	06.08	Близнецы
5	Наталья б.	23.06	Рак
6	Никита В.	08.07	Рак
7	Эдуард М.	22.07,	Рак
8	Кристина П.	10.08	Лев
9	Светлана Т.	14.08	Лев
10	Елена О.	30.08	Дева
11	Эмилия Б.	31.08	Дева
12	Владислав П.	29.08	Дева
13	Диана П.	26.08	Дева
14	Александр С	29.08	Дева
15	Хасан Д.	24.09	Весы
16	Ана Р.	10.10	Весы
17	Петр С.	26.09	Весы
18	Олег И.	09.11	Скорпион
19	Анастасия Д.	16.12	Стрелец
20	Екатерина Н.	05.12	Стрелец
21	Елена К.	29.12	Козерог
22	Никита К.	15.01.	Козерог
23	Анар М.	27.12	Козерог
24	Алексей П.	15.01	Козерог
25	Кирилл Н.	03.03	Рыбы
26	Наталья Витальевна	09.03	Рыбы

И узнал, что в нашем классе представлены все знаки Зодиака, кроме знака Водолей. В количественном отношении знаки распределились следующим образом как указано в Таблице №2

Знак	Название	Количество
♈	Овен	1
♉	Телец	2
♊	Близнецы	1
♋	Рак	3
♌	Лев	2
♍	Дева	5
♎	Весы	3
♏	Скорпион	1
♐	Стрелец	2
♑	Козерог	4
♒	Водолей	0
♓	Рыбы	2

Таблица №2

Более наглядно данные Таблицы № 2 представлены на диаграмме "Знаки Зодиака" (Рис.12)

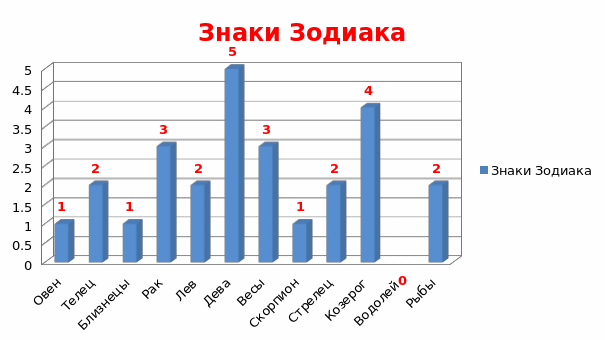
Рис.12

Заключение

В ходе работы над проектом "Звезды на ладони" я познакомился с историей возникновения координат, узнал о различных видах систем координат, их особенностях, происхождении и назначении. Таким образом, можем сделать вывод о том, что без математических знаний о координатах и систем координат вся современная жизнь невозможна. Мы не могли бы определить свое местоположение, местоположение какого - либо объекта на Земле и на небе. Системы координат пронизывают всю практическую жизнь человека: почтовые адреса и номера телефонов, в поезде номер вагона и номер места, в многоэтажном доме номер подъезда и номер этажа; система координат в зрительном зале (номер ряда и номер места); географические координаты (долгота и широта) представлена на картах, туристических маршрутах; система координат используется в шахматах, где вертикали обозначаются цифрами, а горизонтали латинскими буквами; системой координат мы пользуемся, когда играем в «Морской бой».

В своей бытовой и профессиональной деятельности человек регулярно сталкивается с прямоугольной декартовой системой координат, имеющей огромное практическое применение.

Проведя большую работу по изучению зодиакальных созвездий,я пришел к выводу, что мир знаков зодиаков – это та прекрасная грань, которая соединяет человека с загадочным космосом и далёкими звёздами. Изучая знаки Зодиака, построил в программе GeoGebra 12 зодиакальных созвездий на координатной плоскости. Систематизировав полученные знания, я смог провести астрологические исследования учащихся 9 «В» класса.

Список литературы

1. Ф.А.Брокгауз и И.А.Эфрон. - М.; Эксмо; Форум, 2007.- 960с

2.Военно-морской словарь. Гл.ред. В.Н.Чернавин. - Москва.: Военное издательство, 1990. - 511стр., стр.195.

3.словарь Ожегова

4. словарь Д.Н.Ушакова

5.словарь Энциклопедии

6. Энциклопедический словарь юного математика / Сост. А.П.Савин. – М.: Педагогика, 1985- 325с, стр.151.

7.Н. Каменьщиков. Астрономические задачи. Сборник для юношества. Государственное Издательство, Москва.1923.

8. https://astro-world.ru/zodiakalnye-sozvezdiya/

9. Рисунки созвездий на карте звездного неба. [Электронный ресурс]: https://dsastro.ru/ (Дата обращения: 10.12.2020)

10. История математики [Электронный ресурс]: http://festival.1september.ru/2004_2005/index.php?numb_artic=213063- (Дата обращения: 08.12.2020).

11. Школьная математики. [Электронный ресурс]: http://math-prosto.ru (Дата обращения: 11.11.2020)

12.Астрономические задачи [Электронный ресурс]: http://www.astronet.ru/db/msg/1175505/pic/app1.gif.html (Дата обращения: 25.11.2020)