Исследовательская работа "Математические модели в решении задач"

Районный конкурс исследовательских, проектных, творческих работ учащихся   Образовательная область: Математика Секция: Математика  Тема: МАТЕМАТИЧЕСКИЕ МОДЕЛИ В РЕШЕНИИ ЗАДАЧ

Выполнила: Шихова Дарья,

ученица 7 «В» класса

МБОУ «Гимназия №2» г.Зарайска Московской области

Руководитель:

Мережкина Ольга Викторовна,

учитель математики

Очень часто при решении практической задачи удается, изучив условие задачи, построить её математическую модель, на этой модели осуществить решение задачи, а затем перевести результат решения на язык исходной ситуации, т.е. сделать практический вывод.

В этом и состоит могущество математического метода познания природы, широкая прикладная направленность математики.

Цель : оценить практического значения владения методом математического моделирования, широты его использования.

Задачи :

• показать применение метода математического моделирования для исследования и решения задач математики, физики и других научных областей;
• расклассифицировать задачи с применением метода математического моделирования по способам составления математичкой модели и по областям применения;
• показать необходимость формирования умения решать задачи методом математического моделирования для успешного выполнения экзаменационной работы по математике.

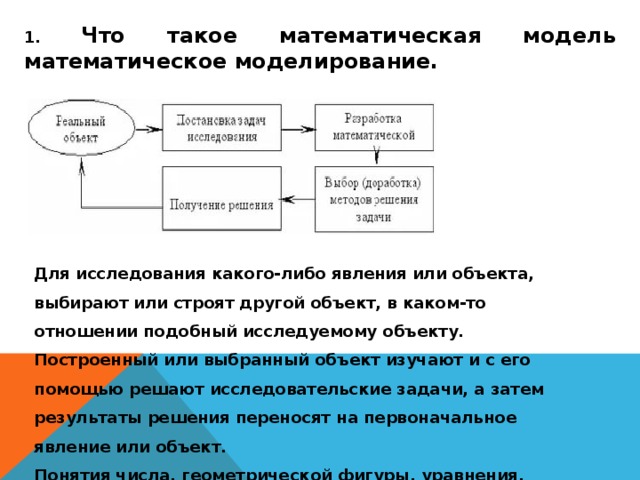
1. Что такое математическая модель математическое моделирование.

Для исследования какого-либо явления или объекта, выбирают или строят другой объект, в каком-то отношении подобный исследуемому объекту. Построенный или выбранный объект изучают и с его помощью решают исследовательские задачи, а затем результаты решения переносят на первоначальное явление или объект.

Понятия числа, геометрической фигуры, уравнения, неравенства, функции являются примерами математических моделей.

Модели окружают нас

Что такое математическая модель

• Графические с рисунком, схемой;
• Графические с графиком;
• Графические с диаграммой;
• Графические табличные;
• Описательные по действиям;
• Описательные «с конца»;
• Задачи прикладной математики

Моя «подклассификация» математических моделей

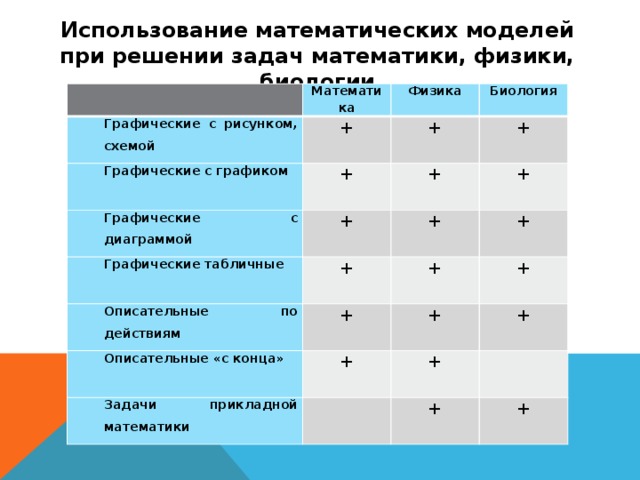
Использование математических моделей при решении задач математики, физики, биологии

Математика

Графические с рисунком, схемой

Физика

+

Графические с графиком

Графические с диаграммой

Биология

+

+

+

Графические табличные

+

+

+

+

+

Описательные по действиям

+

+

+

Описательные «с конца»

+

+

Задачи прикладной математики

+

+

+

+

+

Графические модели с рисунком и схемой

Задача 3.   Паша поехал на дачу на велосипеде, а Саша на мотоцикле. Выехали они одновременно, но так как скорость мотоцикла на 10 км/ч больше скорости велосипеда, то Саша приехал на 2 ч. раньше Паши. Найдите скорость движения каждого мальчика, если расстояние от дома до дачи 40 км.

Решение

Скорость удаления мотоциклиста относительно велосипедиста 10 км/ч, за 2 ч он удалится на 20 км, то есть велосипедист проедет 20 км, а мотоциклист 40 км. Из этого следует, что скорость мотоциклиста в 2 раза больше скорости велосипедиста, и велосипедист 20 км проехал за 2 часа. Найдем скорость велосипедиста 20:2=10 км/ч, а мотоциклиста 20 км/ч.

Ответ: скорость велосипедиста 20:2=10 км/ч, скорость мотоциклиста 20 км/ч.

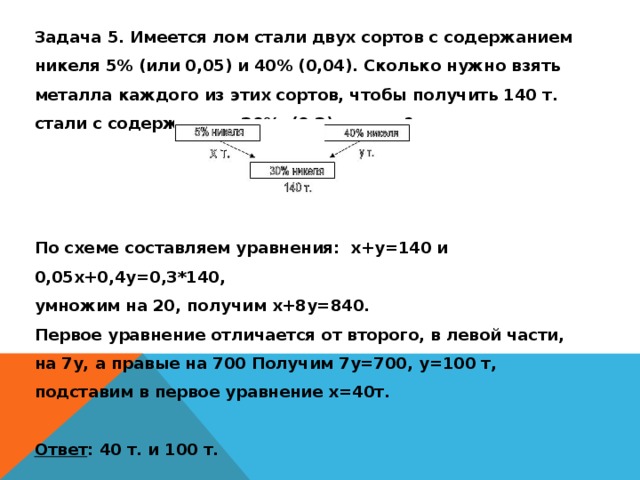
Задача 5.   Имеется лом стали двух сортов с содержанием никеля 5% (или 0,05) и 40% (0,04). Сколько нужно взять металла каждого из этих сортов, чтобы получить 140 т. стали с содержанием 30%  (0,3) никеля?

По схеме составляем уравнения: х+у=140 и 0,05х+0,4у=0,3*140,

умножим на 20, получим х+8у=840.

Первое уравнение отличается от второго, в левой части, на 7у, а правые на 700 Получим 7у=700, у=100 т, подставим в первое уравнение х=40т.

Ответ : 40 т. и 100 т.

Графические модели с таблицей

Задача 12. Четверо ребят – Игорь, Сережа, Миша и Юра – играли во дворе в футбол и разбили окно. Кто разбил окно? – спросила тетя Даша.

Окно разбил или ваш Юра, или Миша, - сказал Сережа.

Я окно не разбивал, - возразил Юра.

Это сделал Миша, - сказал Игорь.

  Нет, Игорь, ты ошибся, - заметил Миша.

  Ну что, задали они тебе задачу? – сказал дядя Вася, слушавший эту беседу. – Могу еще добавить, что трое из этих «футболистов» всегда говорят только правду. А вот четвертого я плохо знаю.

Кто разбил окно? С кем из ребят дядя Вася был мало знаком?

  Говорит

Сережа

Игорь

Юра

Сережа

Игорь

Миша

Разбил (и)

Юра

Миша

Разбил (л)

Не разбивал (и)

Разбил (и)

Не разбивал (л)

Из таблицы видно, что разбил окно Миша. В этой ситуации получается три ответа истинных и один ложный. Следовательно, дядя Вася мало знаком с Мишей. Такое решение используется в информатике.

Задачи на движение

  Задача 13. Из  A  в  B  и из  B  в  A  на рассвете (одновременно) вышли навстречу друг другу (по одной дороге) две старушки. Они встретились в полдень, но не остановились, а каждая продолжала идти с той же скоростью, и первая пришла (в  B)  в 4 часа дня, а вторая (в A) в 9 часов вечера. В котором часу был в этот день рассвет?

Решение . Пусть  х  это время от рассвета до встречи,  S 1 -  это путь, пройденный первой старушкой до встречи,  S 2  - это путь пройденный второй старушкой до встречи, тогда заполним таблицу, зная, что V=S/t.

Из таблицы (или из схемы) получим равенство  S 1 /x=S 2 /4  и  S 2 /x=S 1 /9.  Найдем отношение S 1 /S 2  пройденных путей для обеих старушек, так как скорость остается неизменной, S 1 /S 2 =x/4 (1)   и   S 1 /S 2 =9/x (2).

Так как в выражениях (1) и (2) правые части равны, то будут равны и левые части, x/4=9/x, х 2 =36, х=6 (ч) прошло до встречи в полдень. Значит, рассвет в этот день был в  6 часов утра.

Описательные модели «с конца»

Задача 15.  В Южной Америке есть круглое озеро, где 1 июня каж­дого года в центре озера появляется цветок Виктории Регии. Каждые сутки площадь цветка увеличивается вдвое, и 1 июля он, наконец, покрывает все озеро, лепестки осыпаются на дно. Какого числа площадь цветка составляет половину площади озера?

Решение.  

Данную задачу легче решать с конца . Так как 1 июня покроется все озеро, то накануне площадь будет в 2 раза меньше, то есть  половина озера, а это будет 30 июня.

Ответ: 30 июня площадь цветка составляет половину площади озера.

Задача 16.    Улитка за день залезает вверх по столбу на 3 см, а за ночь, уснув, нечаянно спускается на 2 см. Высота столба 1 м, а наверху лежит вкусная для улитки конфета. Через сколько дней улитка ее достанет?

Решение:

Решим  задачу с конца. За последний день она проползет 3 см, а за сутки она проползает 1 см, то общее количество дней  (3 см за 1 день и 97 см за 97 суток) будет 98 дней.

Ответ: улитка достанет конфету через 98 дней.

В данном случае модель позволяет не осуществлять эксперимент, а заменить расчетами, чтобы не мучить улитку.

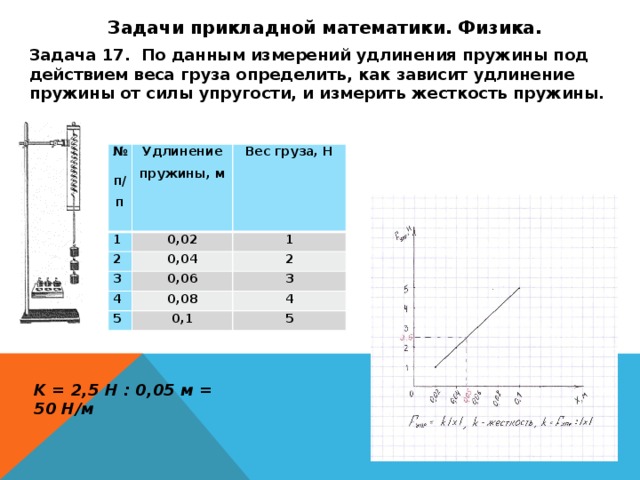
Задачи прикладной математики. Физика.

Задача 17. По данным измерений удлинения пружины под действием веса груза определить, как зависит удлинение пружины от силы упругости, и измерить жесткость пружины.

№

п/п

Удлинение пружины, м

1

2

Вес груза, Н

0,02

0,04

1

3

2

0,06

4

0,08

3

5

4

0,1

5

K = 2,5 H : 0,05 м = 50 Н/м

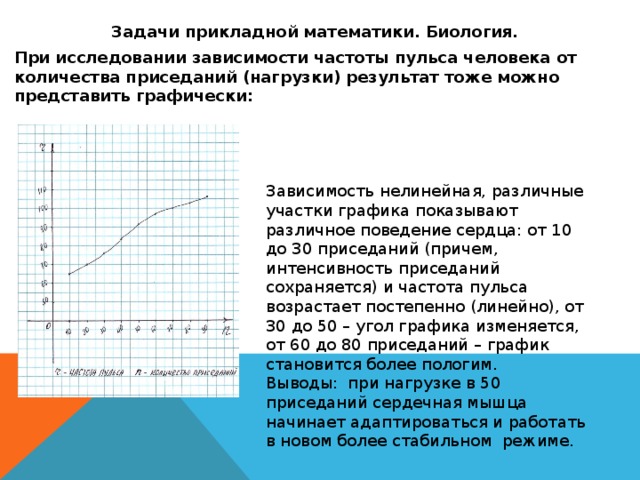
Задачи прикладной математики. Биология.

При исследовании зависимости частоты пульса человека от количества приседаний (нагрузки) результат тоже можно представить графически:

Зависимость нелинейная, различные участки графика показывают различное поведение сердца: от 10 до 30 приседаний (причем, интенсивность приседаний сохраняется) и частота пульса возрастает постепенно (линейно), от 30 до 50 – угол графика изменяется, от 60 до 80 приседаний – график становится более пологим.

Выводы: при нагрузке в 50 приседаний сердечная мышца начинает адаптироваться и работать в новом более стабильном режиме.

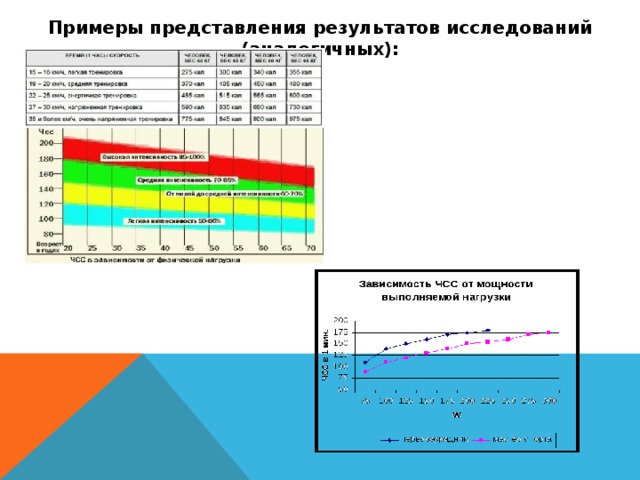
Примеры представления результатов исследований (аналогичных):

Задачи моделирования в текстах ЕГЭ по математике

Использование моделирования обеспечивает:

• качественный анализ задачи,
• осознанный поиск решения,
• обоснованный выбор арифметического действия,
• рациональный способ решения.

Моделирование помогает установить:

• условия, при которых задача имеет решение или не имеет решения;
• как изменятся значение искомой величины в зависимости от изменения данных величин;
• развивает самостоятельность и мышление.

    Моделирование при решение практических задач помогает:

• понять задачу,
• исследовать ее,
• найти рациональный путь решения.

Чертежи, схемы, таблицы помогают:

• обосновать каждый шаг при анализе задачи и в ее решении,
• проверить правильность решения.

  В учебниках алгебры, физики старших классов очень широко можно использовать математическое моделирование при решении более сложных математических и физических задач.

Литература:

1.      А. А. Самарский, П. Н. Вабищев «Математическое моделирование и вычислительный эксперимент, 2000г» (Публикации, интернет)

2.       И. Целищева, С. Зайцева «Моделирование в текстовых задачах» 5-6 классы  газета «Математика» (1 сентября) №33 2002г (стр.6-8), № 34 2002 (стр. 11-13,16)

3.      О. Охтеменко Тема: «Решение задач с помощью рациональных уравнений»  газета «Математика» (1 сентября) №32 2002г (стр.29)

4.      О. Городнова «Учимся решать задачи на «смеси и сплавы»»   газета «Математика» (1 сентября) №36 2004 (стр. 14-18)

5.      М. Кац «Проценты» газета «Математика» (1 сентября) №23 2004г (стр.28-32)

6.      О. Тараканова «Практикум по решению задач» газета «Математика» (1 сентября) №1 2004г (стр.5-8)

7.     А. В. Шевкин «Текстовые задачи» (Москва «Просвещение» 1997г) (стр. 4-5, 8,19-22, 31-33)

8.      В. И. АРНОЛЬД «Задачи для детей от 5 до 15 лет» Москва Издательство МЦНМО 2004

9.      Электронные ресурсы (mathege.ru, infoegehelp.ru)