Конспект урока по теме "Решение задач по теории вероятностей"

МБОУ Ерахтурская средняя общеобразовательная школа

муниципального образования – Шиловский муниципальный район

Рязанской области

Конспект урока

по математике по теме

«Решение задач по теории вероятностей»

11 класс

Выполнила учитель математики

Флорина Т.А.

2015 год

Цель урока: развивать  у учащихся навыки  применения теоретических  знаний  по теме «Решение задач по теории вероятностей».

Образовательные: обобщить и систематизировать знания учащихся по теме

«Теория вероятностей», рассмотреть прототипы задач ЕГЭ по данной теме, предоставить обучающимся возможность проверить свои знания при самостоятельном решении задач.

Развивающие: способствовать развитию памяти, внимания, навыков самооценки и самоконтроля; формированию основных ключевых компетенций (сравнение, сопоставление, контролировать и оценивать свою деятельность, находить и устранять причины возникших трудностей).

Воспитательные: способствовать формированию у учащихся ответственного отношения к учению.

Методы обучения: словесный, наглядный, практический.

Формы работы: индивидуальная, фронтальная, в парах.

Оборудование и материалы для урока:  проектор, экран, ПК для каждого ученика, презентация, индивидуально – дифференцированные карточки для самостоятельной работы в парах, список  сайтов сети Интернет, индивидуально-дифференцированное  домашнее задание.

Пояснение к уроку. 

Данный урок проводится в 11 классе  с целью подготовки к ЕГЭ.

 В настоящее время  важным фактором в обучении  старшеклассников является подготовка  их к ЕГЭ.  Моя методика подготовки основана  на подаче базового и теоретического материала и закреплении его на задачах  в письменной и интерактивной форме, которая позволяет  обеспечить прочное  усвоение знаний, умений и навыков,  развитие способностей учащихся. Также необходимо показать учащимся алгоритмы решения основных тематических заданий.   А вот далее предоставляется свобода ученику в самостоятельной деятельности – повторении и воспроизведении теоретического материала, решении задач. Именно самостоятельная деятельность позволяет  ученику раскрыться, лучше использовать свой творческий потенциал, научит применять теоретическую базу при решении различных задач.

В своей методике подготовки к ЕГЭ я применяю следующие принципы:

1 Многократное повторение учебного материала.

2. Выделение главного при изучении темы.

3. Самостоятельная деятельность учащихся.

4. Систематический опрос и проверка усвоения материала.

5. Дифференцированное обучение.

6. Использую информационные технологии.

Целесообразность использования ИКТ:

• улучшение  наглядности изучаемого материала,

• увеличение количества предлагаемой информации,

• уменьшение времени подачи материала;

• повышение эффективности усвоения учебного материала за счет групповой и самостоятельной деятельности учащихся.

Ход урока

Эпиграфом к нашему уроку я взяла фразу «Считай несчастным тот день или час, в который ты не усвоил ничего нового и ничего не прибавил к своему образованию»

 (Я.А. Коменский)

Скажите, какие задания ЕГЭ по теории вероятностей представляют для вас особую трудность?

Данная задача егэ на вероятность редко встречается, но все же - лучше разберем решение. Здесь представлено 2 способа решения. В первом способе, мы отмечаем на координатном луче 3 промежутка, и отмечаем каждый промежуток как отдельное событие - A,B или C. Из рисунка видно, что x1 когда 12, т.е.  x1= 12, или A=B+C. Подставляя числа из условия задачи, решим уравнение и найдем ответ 0,09.

Следующая задача В10 более стандартна, она взята из реального варианта 2013 года. Здесь мы пользуемся формулой вероятности события, где количество определенных случаев делим на общее число случаев.

Решите ее самостоятельно.

Еще одна задача по теории вероятности, в начале решения которой мы находим число неисправных светильников, затем количество исправных. В конце используем формулу вероятности и получаем ответ 0,994.

Решаем устно.

Стандартная задача ЕГЭ на вероятность, чаще всего встречается. Здесь мы находим число билетов без конуса 25-3=22 и делим их на общее количество билетов: 22/25=0,88.

Интересная задача по теории вероятности на игральные кости. Т.к. каждая игральная кость содержит 6 разных очков (6 сторон или граней): 1,2,3,4,5,6, а всего у нас две кости, то получается что всего 6*6=36 возможных случаев с очками. Посчитаем количество случаев, когда сумма очков у двух костей равна 8: 2 и 6; 3 и 5; 4 и 4; 5 и 3; 6 и 2 - т.е. 5 раз может выпасть 8 очков. Таким образом, по формуле вероятность равна 5/36=0,14.

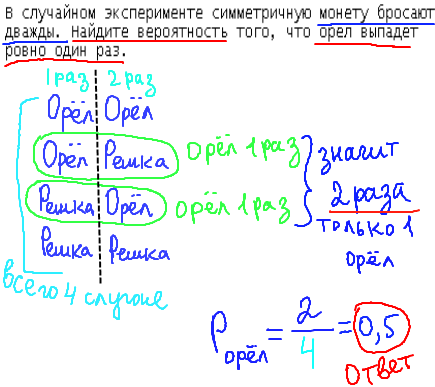
В следующем задании ЕГЭ по математике В10 дана монета, и нужно найти вероятность выпадения одно орла при подбрасывании монеты 2 раза. Посчитаем всего возможных случаев: Орел Орел, Орел Решка, Решка Орел, Решка Решка - т.е. всего 4 случая, в 2-ух из которых орел встречается по 1 разу. Используя формулу вероятности, получим 2/4=0,5.

Решим следующее задание ЕГЭ по математике 2014 года. Всего 16 карточек (групп), где 4 карточки со 2 группой. Значит вероятность вытянуть карточку со 2 группой равна 4/16=1/4=0,25.

В этой задаче ЕГЭ на теорию вероятности, мы из 10 чисел (от 0 до 9) считаем количество четных чисел: 0,2,4,6,8 - т.е. 5 четных чисел, которые делим на общее количество 5/10=0,5.

В этой задаче ЕГЭ по математике предположим, что для выигрыша жребия у команды "Физик" монета должна выпасть орлом. Тогда в 3 матчах будет 3 броска монеты, всего возможных случаев будет 2³=8: Ор Ор Ор, Ор Ор Р, Р Ор Ор, Ор Р Ор, Р Р Р, Р Ор Р, Р Р Ор, Р Ор Ор, где в 3 случаях Орел будет встречаться 2 раза (т.е. команда "Физик" имеет 3 случая выигрыша жребия в 2-ух матчах). Найдем вероятность выигрыша жребия 3/8=0,375.

Решение задач в группах.

Домашнее задание: выполнить задания из открытого банка заданий, ссылка на сайт http://alexlarin.net/ege/2014/b102014.html