Квадратичная функция и ее график.

Раздел долгосрочного планирования:

8.3А Квадратичная функция

Дата:

класс: 8

Тема урока

Квадратичная функция и ее график.

Цели обучения, достигаемые на этом уроке (Ссылка на учебный план)

8.5.1.2

знать свойства и строить графики квадратичной функции вида y=a(x-m)² ; y=ax²+n ; y=a(x-m)² + n, a;

8.5.1.3.

знать свойства и строить график квадратичной функции вида y=ax²+вх + с

8.5.1.4

находить значения функции по заданным значениям аргумента и находить значение аргумента по заданным значениям функции

Цель урока

Все: знают определение квадратичной функции и знают её свойства.

Большинство: умеют строить график квадратичной функции. находить значения функции по заданным значениям аргумента и выполнять обратную задачу.

Некоторые: могут использовать свойства квадратичной функции.

Критерии оценивания

Определяют квадратичную функцию, строят её график, знают и применяют свойства квадратичной функции.

Языковые задачи

Обучающийся перечисляет основные этапы и шаги построения графиков квадратичных функций, использует свойства квадратичной функции

Термины: Аргумент, функция, максимум и минимум, нули функции, возрастание и убывание функции

Сочетания:

- для того, чтобы найти координаты вершины параболы…

- чтобы определить точки пересечения с осями координат…

Воспитание ценностей

1. Умение работать в группе

2. Развитие коммуникативных способностей

3. Уважение и принятие точек зрения своих одноклассников

4. Оказание взаимопомощи.

Межпредметная связь

Физика ( формулы кинетической и потенциальной энергии )

Предыдущие знания

Решают квадратные уравнения

Ход урока

Запланированные этапы урока

Виды упражнений, запланированных на урок:

Ресурсы

Начало урока

Приветствие. «Я тебе желаю на уроке»

Психологический настрой учащихся

Сообщение темы урока. Формулировка целей урока совместно с учащимися.

Середина урока

5 мин

1. Актуализация знаний учащихся. Математический диктант «да-нет»

Цель: концентрация внимания учащихся

Верно «+», неверно «-».

1.Функция у=-6+4х² -5х является квадратичной

2.Графиком этой функции является прямая

3.Областью определения функции является множество всех действительных чисел

4.Эта функция имеет наибольшее значение

5.График функции симметричен относительно начала координат

6.Если телу сообщить начальную скорость, направленную под углом к горизонту, то траектория движения этого тела будет иметь такой же вид, как график квадратичной функции

7.Правда ли, что графиком зависимости кинетической энергии тела от его скорости является парабола?

8.Правда ли, что графиком зависимости потенциальной энергии тела от его высоты является парабола?

Самопроверка ( + - + - + + + - )

Самооценка: Кто все задания выполнил верно, погладьте себя по голове

II. Работа в парах. Метод «таблица Фила»

Повторение изученного материала и систематизация знаний

Учащимся необходимо завершить определения и формулировки.

Взаимопроверка.

Ответы на ИД

Обратная связь

Учитель:

По каждому пункту задает вопросы по уровню выполнения задания:

1. Кто неверно закончил 1-ое, 2-ое, 3-тье и т.д. определения и формулировки?

2. В чем заключалась ошибка?

3. Почему я ее допустил?

4. Дайте верный ответ.

Закрепление знаний учащихся и выработка навыков.

1. 3.ИР. Самостоятельная работа.

Уровень А

Задание 1. Определите направление ветвей и координаты вершины параболы:

Дескриптор:

Обучающийся

- определяет направление ветвей параболы;

- находит координаты вершины параболы.

Задание 2. Установите соответствие между функциями и их графиками:

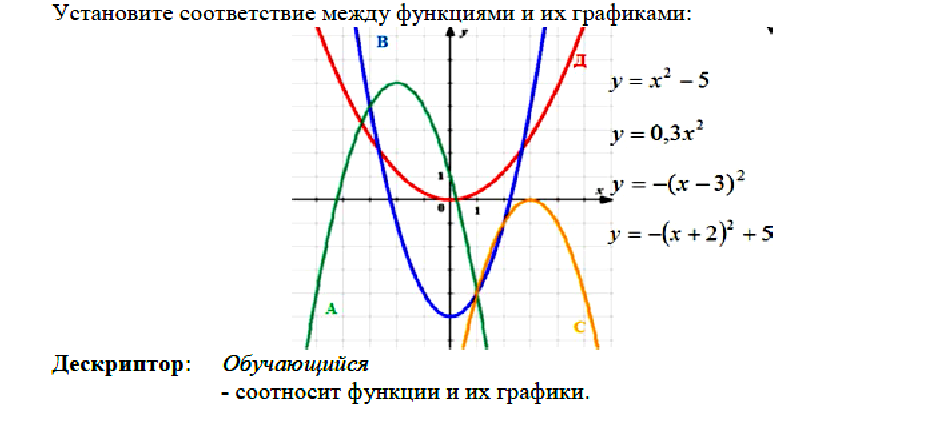
Дескриптор:

Обучающийся - соотносит функции и их графики.

Уровень В:

Задание 1.

Дана функция у = - х ² + 2х + 8. Заполните таблицу

Дескриптор:

Обучающийся

- находит абсциссу вершины параболы

- находит ординату вершины параболы

- находит точки пересечения с осью Ох

- находит точку пересечения с осью Оу

- находит точку, симметричную ей

Задание 2. Используя шаблон параболы у = х² , построить графики функций:

y= ( x-3 )² ; y= x²+4 ; y= ( x+ 5 )² – 4; ( x -1 )²+6

Дескриптор:

Обучающийся

-определяет координаты вершин парабол

- определяет направление ветвей парабол

Форма оценивания: самооценивание по образцу.

Обратная связь:

В каких заданиях у вас возникали затруднения? Почему?

Деление на группы: По карточкам.

Учитель раздает карточки, на которых записаны различные функции. Каждый учащийся берет одну карточку, затем в одну группу объединяются те учащиеся, у которых записаны функции, не являющиеся квадратичными, в другую – те, у кого записаны параболы, ветви которых направлены вниз, в третью-параболы, ветви которых направлены вверх.

4. ГР. Составление постера по группам и защита спикера.

Задание 1 группе:

Исследование, проведенные в одной крупной производственной компании, показали, что производительность труда в течение рабочего времени меняется в зависимости от времени работы по закону N(t) = - 0,2t ² +1,6t +3. Постройте график функции, считая, что рабочий день равен 8 ч и ответьте на вопросы:

1) В какой промежуток времени растет производительность труда?

2) В какое время производительность труда достигает максимума?

3) Промежуток рабочего дня, во время которого производительность труда падает?

4) Сравните производительность труда через 2 часа и через 6 часов после начала работы. В какое время производительность выше?

Дескриптор:

Обучающийся

- строит график функции;

- находит промежутки возрастания функции;

- определяет по графику максимальное значение функции;

- находит значение аргумента, при котором функция достигает максимального значения;

- находит производительность труда по заданным значениям времени;

- сравнивает найденные значения и делает вывод.

Задание 2 группе:

График изменения кинетической энергии тела от его скорости задан формулой Е_к = -v² + 2v +3. Постройте график функции и ответьте на вопросы:

1) При каком значении скорости значении энергии будет максимальным?

2) Найдите промежутки возрастания и убывания кинетической энергии

3) Сравните значения энергии при v=1 и v=3

4) Объясните результат, полученный в задании № 3.

Дескриптор:

Обучающийся

- строит график функции;

- находит значение аргумента, при котором функция достигает максимального значения;

- находит промежутки возрастания и убывания функции;

- сравнивает значения функции по заданным значениям аргумент

- делает вывод.

Задание 3 группе:

На полигоне, с высоты в два метра, под углом к горизонту была выпущена сигнальная ракета. Изменение высоты её полёта h (метры) в зависимости от времени движения t (секунды) описывается формулой h = 2 + 21t − 5t² .

Постройте график зависимости высоты поднятия ракеты от времени и ответьте на вопросы:

1) В какое время ракета поднимется на высоту 16 м? В какое время она окажется на той же высоте при спуске?

2) На какой высоте будет находиться ракета через 3,5 с полёта?

3) Укажите наибольшую высоту подъёма ракеты.

4) Сколько времени потребовалось ракете, чтобы подняться на максимальную высоту?

Дескриптор:

Обучающийся

- строит график функции

- находит значение функции;

- находит значение аргумента;

- определяет по графику наибольшее значение функции;

- находит при каком значении аргумента функция достигает своего наибольшего значения.

Защита постера.

Оценивание. Прием «Две звезды, одно пожелание».

Фигурки «плюс» и

«минус»

Слайд с верными ответами

Таблица

Фила

Слайд с верными ответами, ИД

Раздаточный материал

Готовые листы ответов

Раздаточный материал

Конец урока

Рефлексия. Метод «Воздушный шар»

На стикерах написано:

Зеленый цвет: Мне помогло на уроке понять тему то, что…

Желтый цвет: Мне было трудно на уроке из-за того, что…

Красный цвет: Мне на уроке мешало то, что…

Учащиеся приклеивают зеленые стикеры на уровне шара, желтые стикеры на уровне корзины, красные стикеры в нижней части корзины шара.

Стикеры 3-х цветов.

Изображение воздушного шара

Дифференциация – каким способом вы хотите больше оказывать поддержку? Какие задания вы даете ученикам более способным по сравнению с другими?

Оценивание – как Вы планируете проверять уровень усвоения материала учащимися?

Охрана здоровья и соблюдение техники безопасности

Самостоятельная работа и домашнее задание с учетом индивидуальных особенностей учащихся

Ученик к крнцу урока будет строить графики квадратичной функции вида y=a(x-m)² ; y=ax²+n ; y=a(x-m)² + n, a; y=ax²+вх + с;

находить значения функции по заданным значениям аргумента и находить значение аргумента по заданным значениям функции

Методы и приемы, испольуемые на уроке: актуализация знаний в форме математического диктанта; самостоятельная дифференцированная работа,

групповая работа;

взаимоцениевание между группами;

взаимооценивание между учениками;

формативное оценивание.

Эмоциональный настрой

Движение учащихся во время формирования групп