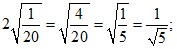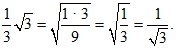Лекция 2
Числа и вычисления. Выражения и преобразования.
План
Числа и вычисления.
Выражения и преобразования.
1. Числа и вычисления.
Натуральные числа, получаемые при естественном счёте; множество натуральных чисел обозначается N; N = {0, 1, 2, 3, …}.
Целые числа, получаемые объединением натуральных чисел с множеством отрицательных чисел и нулём, обозначаются
Z = {–2, –1, 0, 1, 2, …}.
Рациональные числа — числа, представленные в виде дроби m/n (n ≠ 0), где m — целое число, а n — натуральное число.
Для рациональных чисел определены четыре «классические» арифметические действия: сложение, вычитание, умножение и деление (кроме деления на ноль).
Для обозначения рациональных чисел используется знак Q. 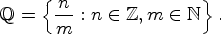
Действительные (вещественные) числа представляют собой расширение множества рациональных чисел. Множество вещественных чисел обозначается R.
Кроме рациональных чисел, R включает множество иррациональных чисел, не представимых в виде отношения целых. Кроме подразделения на рациональные и иррациональные, действительные числа также подразделяются на алгебраические и трансцендентные. При этом каждое трансцендентное число является иррациональным, каждое рациональное число — алгебраическим.
Иррациональные числа.
1) любое рациональное число изображается бесконечной десятичной дробью;
2) всякое иррациональное число изображается бесконечной десятичной дробью;
3) любое действительное число может быть представлено в виде бесконечной десятичной дроби;
4) всякая бесконечная десятичная дробь представляет действительное число (обратное утверждение).
| Обозначение (имя) | Что означает имя |
| N | Множество натуральных чисел |
| Z | Множество целых чисел |
| Q | Множество рациональных чисел |
| R | Множество действительных чисел |
Свойства сложения и умножения:
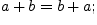
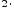
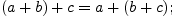
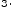
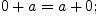
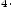
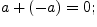
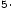
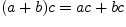 ;
;
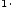
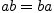 ;
;
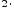
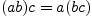 ;
;
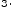
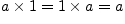 ;
;
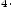
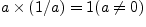
определение арифметического квадратного корня
Арифметическим квадратным корнем из числа а называется неотрицательное число, квадрат которого равен а.
основные свойства квадратного корня
1) (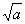 )2= а,
)2= а, 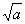 ≥ 0.
≥ 0.
2) 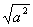 =
=  .
.
3) 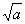
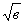 , если ав0.
, если ав0.
4) 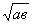 =
=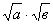 , если а≥ 0,в ≥ 0
, если а≥ 0,в ≥ 0
5) 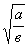 =
=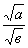 , если а≥ 0, в0.
, если а≥ 0, в0.
2. Выражения и преобразования.
1) Упростите:
а)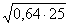 Решение:
Решение: 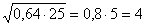 .
.
б) 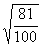 Решение:
Решение: 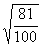 =
=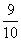 .
.
в) 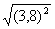 Решение:
Решение: 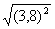 =
=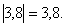

г) 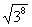 Решение:
Решение: 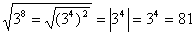
2) Внеси множитель под знак корня:
а) 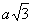 Решение:
Решение: 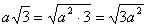
б) 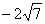 Решение:
Решение: 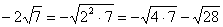
(1 – 2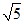 )2 = 1 – 4
)2 = 1 – 4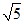 + 20 = 21 – 4
+ 20 = 21 – 4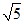 (иррац.).
(иррац.).
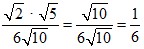 (рац.).
(рац.).
2). Принадлежит ли отрезку [1,57; 1,58] число:
1,57001 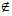 [1,57; 1,58]; 1,581
[1,57; 1,58]; 1,581 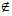 [1,57; 1,58]; 1
[1,57; 1,58]; 1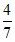
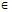 [1,57; 1,58], 1
[1,57; 1,58], 1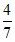 ≈ 1,571…
≈ 1,571… 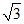
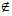 [1,57; 1,58],
[1,57; 1,58], 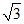 ≈ 1,7.
≈ 1,7. 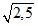
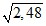
3). Вычислите:
а) 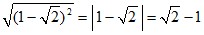 ; б)
; б) 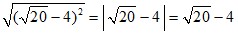 ; в)
; в) 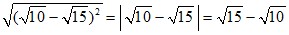 ; г)
; г) 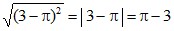 .
.
4). Выберите из чисел:
0,57; –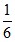 ;
; 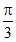 ;
; 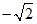 ; 5; 1 –
; 5; 1 –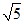 ;
; 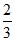 ;
; 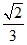 ; –18
; –18
а) положительные рациональные числа;
б) иррациональные числа;
в) отрицательные числа.
5). Запишите на символическом языке следующие утверждения:
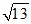 – действительное число;
– действительное число;
0,03 – рациональное число;
–400 – не является натуральным числом;
24 – целое число;
р – не является рациональным числом.
6). Запишите и сравните пары чисел:
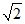
 1,411;
1,411; 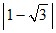
 0,777;
0,777;
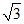
 1,731;
1,731; 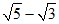
 0,555;
0,555;
–р  –3,214;
–3,214; 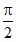
 1,566.
1,566.
7). Запишите числа и расположите их в порядке возрастания:
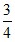 ; 0,751; 0,7501; 0,750101.
; 0,751; 0,7501; 0,750101.
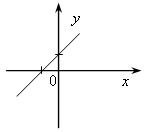
8). На рисунке изображены графики функций вида у = kx + b.
Установите соответствие между графиками и знаками коэффициентов k и b.
а) k 0, b 0; б) k 0, b 0.
1) 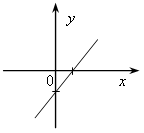 2)
2) 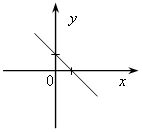 3)
3) 
9). Найдите значение выражения.
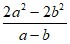 при a = 3,4; b = –5,4.
при a = 3,4; b = –5,4.
Решение. 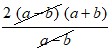 = 2 (3,4 – 5,4) = 2 · (–2) = –4.
= 2 (3,4 – 5,4) = 2 · (–2) = –4.
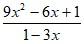 при х =
при х = 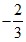 .
.
Решение.
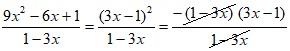 = 1 – 3х = 1 + 2 = 3.
= 1 – 3х = 1 + 2 = 3.
3) 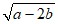 при a = 7, b = –2,5.
при a = 7, b = –2,5.
Решение. 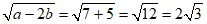 .
.
10). Преобразуйте дроби:
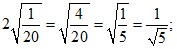
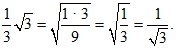
1. Вычислите значение каждого из данных выражений и укажите, какие из них относятся к отрицательным рациональным числам; к положительным иррациональным числам:
а) –2 · 30 – 17 · 0,2;
б) 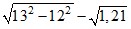 ;
;
в) 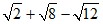 .
.
2. Найдите значения выражений при указанных значениях букв. Укажите, есть ли среди ответов натуральные числа; отрицательные иррациональные числа:
а) –2а2 + b2 при а =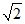 , b =
, b =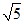 ;
;
б) ab – ac при а = 0,7, b = 1,4, с = –0,6;
в) –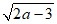 при а = 4,5.
при а = 4,5.
Вопросы для закрепления пройденного материала.
1.Какие числа называются натуральными?
2.Какие числа называются целыми?
3. Какие числа называются рациональными?
Литература
1.Алимов Ш .А, Колягин Ю.М, Ткачева М. В. Алгебра и начала математического анализа, 10-11 классы. Учебник для учащихся общеобразовательных учреждений( базовый и углубленный уровни)- М: Просвещение, 2022.
2.Мордкович А.Г., Семенов П.В. Алгебра и начала математического анализа, 10 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений. – М.: Мнемозина, 2009.
3.Виленкин Н.Я., Ивашев-Мусатов О.С., Шварцбурд С.И. Алгебра и математический анализ для 10 класса (учебное пособие для учащихся школ и классов с углубленным изучением математики). – М.: Просвещение, 1996.
4.Колягин Ю.М., Сидоров Ю.В., Ткачева М.В., Федорова М.В., Шабунин М.И. Алгебра и начала математического анализа, 10 класс. Учебник для учащихся общеобразовательных учреждений (профильный уровень). – М.: Мнемозина, 2009.






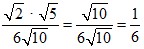 (рац.).
(рац.). 2)
2)  3)
3) 
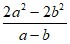 при a = 3,4; b = –5,4.
при a = 3,4; b = –5,4.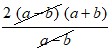 = 2 (3,4 – 5,4) = 2 · (–2) = –4.
= 2 (3,4 – 5,4) = 2 · (–2) = –4.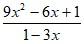 при х =
при х = 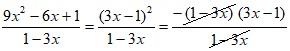 = 1 – 3х = 1 + 2 = 3.
= 1 – 3х = 1 + 2 = 3.