Предмет и задачи математической статистики. Генеральная и выборочная статистические совокупности. Полигон и гистограмма. Выборочный метод
Математической статистикой называется наука, занимающаяся методами обработки экспериментальных данных, полученных в результате наблюдений над случайными явлениями.
Первая задача математической статистики: указать способы сбора и группировки статистических данных, полученных в результате экспериментов.
Вторая задача математической статистики: разработать методы анализа статистических данных.
Ко второй задаче относятся:
Оценка неизвестных параметров (вероятности события, функции распределения и её параметров и т.д.) с построением доверительных интервалов (методы оценивания).
Проверка статистических гипотез о виде неизвестного распределения и параметров распределения (методы проверки гипотез).
При этом решаются следующие в порядке сложности и важности задачи:
Описание явлений, то есть, упорядочение поступившего статистического материала, представление его в наиболее удобном для обозрения и анализа виде (таблицы, графики).
Анализ и прогноз, то есть приближённая оценка характеристик на основании статистических данных. Например, приближённая оценка математического ожидания и дисперсии наблюдаемой случайной величины и определение погрешностей этих оценок.
Выработка оптимальных решений. Например, определение числа опытов n, достаточного для того, чтобы ошибка от замены теоретических числовых характеристик их экспериментальными оценками не превышала заданного значения. В связи с этим возникает задача проверки правдоподобия гипотез о параметрах распределения и о законах распределения случайной величины, решением которой является возможность сделать один из выводов:
– отбросить гипотезу, как противоречащую опытным данным;
– принять гипотезу, считать ее приемлемой.
Математическая статистика помогает экспериментатору лучше разобраться в опытных данных, полученных в результате наблюдений над случайными явлениями; оценить, значимы или не значимы наблюдаемые факты; принять или отбросить те или иные гипотезы о природе случайных явлений.
Генеральной совокупностью называют полный набор всех возможных N значений дискретной случайной величины Х. Практически сложно получить полную информацию о случайной величине. Поэтому случайным образом отбирают объекты, которые называется выборкой, при этом число – n называется объемом выборки. Выборку делают либо из ранее полученных результатов, либо планируют эксперимент. По результатам выборки строят простой статистический ряд в виде таблицы, состоящей из двух строк, в первой – порядковый номер измерения, во второй – его результат xi. Затем производят группировку данных. Вначале xi располагают в порядке возрастания, интервал наблюдаемых значений случайной величины разбивают на последовательные непересекающиеся частичные интервалы, далее подсчитывают количество значений xi, попавших в каждый интервал, т.е. ni. Таким образом, получается группированный статистический ряд или статистическое распределение выборки. Статистическим распределением выборки или статистическим рядом называют перечень вариант и соответствующих им частот или относительных частот.
Пример 1. После группировки данных в выборке статистический ряд задан таблицей 6.1 (где объем выборки n = 15).
Таблица 6.1
| i | 1 | 2 | 3 | 4 |
| xi | 2 | 3 | 5 | 10 |
| ni | 5 | 5 | 3 | 2 |
В таблице 6.1 значения xi называют вариантами. Последовательность вариант, записанных в возрастающем порядке (вся строка xi) называется вариационным рядом. Число наблюдений ni называют частотами, i – номер варианты.
Учитывая, что 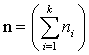 – это объем выборки, можно найти относительную частоту pi=ni/n, наблюдаемого значения xi – варианты, k – количество вариант.
– это объем выборки, можно найти относительную частоту pi=ni/n, наблюдаемого значения xi – варианты, k – количество вариант.
Тогда таблица 6.1 будет иметь вид:
Таблица 6.2
| i | 1 | 2 | 3 | 4 |
| xi | 2 | 3 | 5 | 10 |
| ni/n | 0,33 | 0,33 | 0,2 | 0,14 |
Табличные данные могут быть представлены графически в виде полигона или гистограммы. Если выборка задана в виде отдельных точек, а не интервалов, тогда строят полигон частот. Полигоном частот называется ломанная, отрезки которой соединяют точки (x;; ni/n). На рис.6.1 изображен полигон относительных частот, приведённых в таблице 6.2.
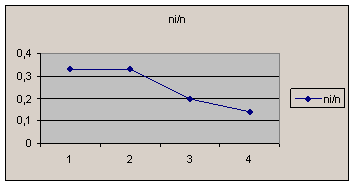
Рис. 6.1. Полигон
Пример 2. В этом примере наблюдаемые значения случайной величины после группировки данных в выборке разбиты на последовательные непересекающиеся частичные интервалы. В результате получается статистический ряд, который задан таблицей 6.3.
Таблица 6.3
| i | 1 | 2 | 3 | 4 |
| xi | 0-2 | 2-4 | 4-6 | 6-8 |
| ni | 5 | 10 | 12 | 3 |
Данную таблицу можно представить через относительную частоту pi =ni/n (где объем выборки n = 30).
Таблица 6.4
| i | 1 | 2 | 3 | 4 |
| xi | 0-2 | 2-4 | 4-6 | 6-8 |
| рi=ni/n | 0,17 | 0,33 | 0,4 | 0,1 |
При этом частоты рi удовлетворяют условию 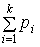 =1. Если выборка задана в виде интервалов, тогда строят гистограмму.
=1. Если выборка задана в виде интервалов, тогда строят гистограмму.
Гистограммой частот называется ступенчатая фигура, состоящая из прямоугольников, основаниями которых служат интервалы xi, их высоты равны рi =ni/n (плотности относительной частоты). На рис. 6.2 изображена гистограмма относительных частот, приведённых в таблице 6.4.
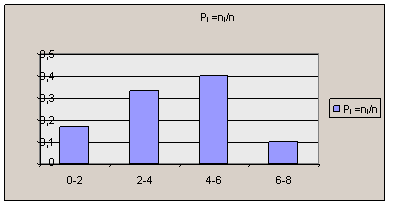
Рис. 6.2. Гистограмма
Контрольные вопросы:
Чем занимается математическая статистика?
Что называется генеральной совокупностью?
Что такое выборка? Объем выборки?
Что такое вариационный ряд? Частоты?
Что называют полигоном частот? Гистограммой частот?


















