По определению
арксинуса числа для каждого x∈[−1;1] определено одно число y=arcsinx
Тем самым на отрезке [−1;1] задана функция y=arcsinx,−1≤x≤1
Функция y=arcsinx является обратной к функцииy=sinx, где −π2≤x≤π2
Поэтому свойства функции y=arcsinx можно получить из свойств функции y=sinx
График функции y=arcsinx симметричен графику функцииy=sinx, где −π2≤x≤π2 относительно прямой y=x

График функции y=arcsinx
Основные свойства функции y=arcsinx
1. Область определения - отрезок [−1;1]
2. Множество значений - отрезок [−π2;π2]
3. Функция y=arcsinx - возрастает.
4. Функция y=arcsinx является нечётной, так как arcsin(−x)=−arcsinx
Свойства функции арксинус
1. y = arcsin x является нечетной функцией;
2. Функция арксинус - возрастающая функция;
3. Область определения функции арксинус от -1 до 1;
4. Множество значений функции арксинус от -П/2 до П/2.
График функции арксинус
График функции y = arcsin x
Свойства функции arcsin .
- arcsin (-x) = - arcsin x функция нечетна,
- arcsin x > 0 при 0 < x ≤ 1,
- arcsin x = 0 при х=0,
- arcsin x > 0 при -1 ≤ х < 0,
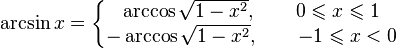 ,
, ,
,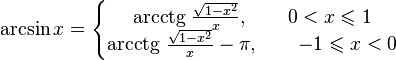 .
.
График арксинуса.

Получение функции arcsin .
Есть функция y = sin x. На всей своей области определения она кусочно-монотонная, таким образом, обратное соответствие y = arcsin x не является функцией. Поэтому рассматриваем отрезок, на котором она только возрастает и принимает каждое значение области значений — 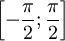 . Т.к. для функции y = sin x на интервале
. Т.к. для функции y = sin x на интервале 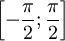 все значения функции получается при только одном значении аргумента, значит, на этом отрезке есть обратная функция y = arcsin x, у которой график является симметричным графику функции y = sin x на отрезке
все значения функции получается при только одном значении аргумента, значит, на этом отрезке есть обратная функция y = arcsin x, у которой график является симметричным графику функции y = sin x на отрезке 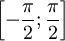 относительно прямой y = x.
относительно прямой y = x.
Так как функция y=sin x определена на промежутке [-π/2;π/2] и принимает на этом промежутке все значения [-1; 1], то область определения арксинуса — промежуток [-1; 1], область значений —[-π/2;π/2].
Таблица значений синуса из промежутка [-π/2; π/2] —


Соответственно, таблица значений арксинуса —









 График функции y=arcsinx
Основные свойства функции y=arcsinx
1. Область определения - отрезок [−1;1]
2. Множество значений - отрезок [−π2;π2]
3. Функция y=arcsinx - возрастает.
4. Функция y=arcsinx является нечётной, так как arcsin(−x)=−arcsinx
График функции y=arcsinx
Основные свойства функции y=arcsinx
1. Область определения - отрезок [−1;1]
2. Множество значений - отрезок [−π2;π2]
3. Функция y=arcsinx - возрастает.
4. Функция y=arcsinx является нечётной, так как arcsin(−x)=−arcsinx

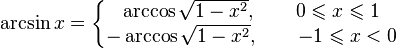 ,
, ,
,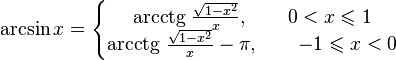 .
.
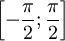 . Т.к. для функции y = sin x на интервале
. Т.к. для функции y = sin x на интервале 













