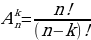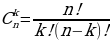9 класс Тема 2 Квадратичная функция, функции и их свойства, квадратный трёхчлен. Алгебра
1.Какая переменная называется независимой переменной? ( переменная ,значение которой выбирается произвольно, называется независимой переменной) 2.Какая переменная называется зависимой переменной? (переменная, значение которой определяется выбранным значением независимой переменной, называют зависимой переменной)
3.Что называется функцией ? ( функцией называется такая зависимость переменной у от переменной х, при которой каждому значению переменной х соответствует единственное значение переменной у) 4.Что называется аргументом? ( независимую переменную иначе называют аргументом)
5.Что называют значением функции? ( значение зависимой переменной называют значением функции)
6.Что называется областью определения функции ? (все значения, которые принимает независимая переменная, образует область определения функции)
7.Что называют областью значений функции? (все значения, которые принимает зависимая переменная, образует область значения функции)
8.Что называется графиком функции ? (графиком функции называется множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты - соответствующим значениям функции)
9.Какая функция называется прямой пропорциональностью ? (прямой пропорциональностью называется функция, которую можно задать формулой вида 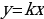 , где х - независимая переменная ,
, где х - независимая переменная , 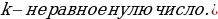
10.Что называется коэффициентом прямой пропорциональности ? (число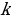 в формуле
в формуле 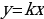 называется коэффициентом прямой пропорциональности )
называется коэффициентом прямой пропорциональности )
11.Что представляет график прямой пропорциональности? (график прямой пропорциональности представляет собой прямую , проходящую через начало координат)
12. От чего зависит расположение графика функции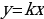 в координатной плоскости? (расположение графика функции
в координатной плоскости? (расположение графика функции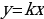 в координатной плоскости зависит от коэффициента
в координатной плоскости зависит от коэффициента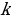 )
)
13.Как расположен график функции 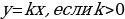 ? ( график прямой пропорциональности расположен в первой и третьей координатных четвертях)
? ( график прямой пропорциональности расположен в первой и третьей координатных четвертях)
14. Как расположен график функции 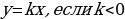 ? ( график прямой пропорциональности расположен во второй и четвертой координатных четвертях)
? ( график прямой пропорциональности расположен во второй и четвертой координатных четвертях)
15. Какая функция называется линейной функцией ? (линейной функцией называется функция, которую можно задать формулой вида 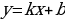 , где x – независимая переменная , k и b – некоторые числа)
, где x – независимая переменная , k и b – некоторые числа)
16.Что является графиком линейной функции? (графиком линейной функции является прямая )
17. Что называется угловым коэффициентом прямой - графика функции 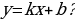 (число
(число 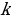 называется угловым коэффициентом прямой - графика функции
называется угловым коэффициентом прямой - графика функции 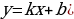
18.Когда графики линейных функций пересекаются ? ( если угловые коэффициенты прямых, являющихся графиками двух линейных функций, различны, то эти прямые пересекаются)
19. Когда графики линейных функций параллельны ? ( если угловые коэффициенты прямых, являющихся графиками двух линейных функций, одинаковы, то эти прямые параллельны.)
20. Дайте определение функции , возрастающей в промежутке (функция называется возрастающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует большее значение функции)
21. Дайте определение функции , убывающей в промежутке (функция называется убывающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует меньшее значение функции)
22. Дайте определение квадратного трёхчлена (квадратным трёхчленом называется многочлен вида 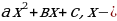 переменная, а, в и с некоторые числа, причём а
переменная, а, в и с некоторые числа, причём а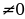 )
)
23. Сколько корней может иметь квадратный трёхчлен?
( если D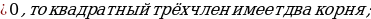
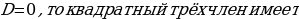 один корень;
один корень; 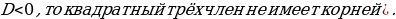
24. Сформулируйте и запишите теорему о разложении на множители квадратного трёхчлена, имеющего корни ( если х1 и х2 – корни квадратного трёхчлена 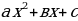 , то
, то 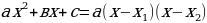 .)
.)
25 . Всегда ли можно разложить квадратный трёхчлен на множители ( нет, если квадратный трёхчлен не имеет корней , то его нельзя разложить на множители , являющиеся многочленами первой степени)

9 класс Тема 2 Квадратичная функция, степенная функция, корень п- ой степени. Алгебра 1.Сформулируйте определение квадратичной функции ( квадратичной функцией называется функция, которую можно задать формулой у = ax2+ bx + c, x –независимая переменная, a ,b и c- некоторые числа, причём a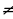 0 )
0 )
2. Что является областью определения квадратичной функции ? (областью определения квадратичной функции является множество всех чисел)
3.Сформулируйте свойства квадратичной функции у = aх2 , если а 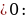
1. Если х = 0, то у = 0. График функции проходит через начало координат.
2.Если х ≠ 0, то у 0 . График функции расположен в верхней полуплоскости.
3.Противоположным значениям аргумента соответствуют равные значения функции. График функции симметричен относительно оси оу.
4.Функция убывает в промежутке (- ∞;0] и возрастает в промежутке [0;+∞).
5.Наименьшее значение , равное нулю, функция принимает при х = 0, наибольшего значения функция не имеет. Областью значений функции является промежуток[0;+∞].
4.Сформулируйте свойства квадратичной функции у = aх2 , если а 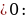
1. Если х = 0, то у = 0. График функции проходит через начало координат.
2.Если х ≠ 0, то у График функции расположен в нижней полуплоскости.
3.Противоположным значениям аргумента соответствуют равные значения функции. График функции симметричен относительно оси оу.
4.Функция возрастает в промежутке (- ∞;0] и убывает в промежутке [0;+∞).
5.Наибольшее значение , равное нулю, функция принимает при х = 0, наименьшего значения функция не имеет. Областью значений функции является промежуток (- ∞; 0].
5.Как из графика функции у = aх2 можно получить график функции у = aх2 + п? (график функции у = aх2 + п является параболой, которую можно получить из графика функции у = aх2 с помощью параллельного переноса вдоль оси Оy на п единиц вверх, если п 0, или на - п единиц вниз , если п
6. Как из графика функции у = aх2 можно получить график функции у = а( х – т)2 ? (график функции у = a ( х – m) 2 является параболой, которую можно получить из графика функции у = aх2 с помощью параллельного переноса вдоль оси Ох на m единиц вправо, если m 0, или на - m единиц влево , если m
7.Как из графика функции у = aх2 можно получить график функции у = а( х – т)2+ п (график функции у = а( х – т)2+ п является параболой, которую можно получить из графика функции у = aх2 с помощью двух параллельных переносов: сдвига вдоль оси Ох на m единиц вправо, если m 0, или на - m единиц влево , если m вдоль оси Оy на п единиц вверх, если п 0, или на - п единиц вниз , если п)
8. Что представляет собой график функции у = aх2+ bx+ c? ( график функции у = aх2+ bx+ c? является параболой)
9.Как построить график квадратичной функции? Чтобы построить график квадратичной функции, нужно:
1)найти координаты вершины параболы и отметить её в координатной плоскости;
2)построить ещё несколько точек , принадлежащей параболе;
3)соединить отмеченные точки плавной линией.
10.Какую функцию называют степенной функцией с натуральным показателем?(функцию, заданной формулой у = хп. , где х – независимая переменная, а п – натуральное число)
11.Сформулироватьсвойства степенной функции с чётным показателем.
1. Если х = 0, то у = 0. График функции проходит через начало координат.
2.Если х ≠ 0, то у 0 . Это следует из того, что чётная степень как с положительного, так и отрицательного числа положительна. График функции расположен в первой и второй координатных четвертях
3.Противоположным значениям аргумента соответствуют равные значения функции. Это следует из того , что при чётном п равенство ( - х )п = хп верно при любых значениях х.
4.Функция возрастает в промежутке [0;+∞) и убывает в промежутке (- ∞;0] .
5.Область значений функции есть множество неотрицательных чисел.
12. Сформулировать свойства степенной функции с нечётным показателем.
1. Если х = 0, то у = 0 . График функции проходит через начало координат.
2.Если х 0, то у 0 ; если х . График функции расположен в первой и третьей координатных четвертях.
3.Противоположным значениям аргумента соответствуют противоположные значения функции. Это следует из того , что при нечётном п равенство ( - х )п = - хп верно при любых значениях х.
4.Функция возрастает на всей области определения.
5.Область значений функции есть множество действительных чисел
13. Дайте определение корня п – й степени ( корнем п – й степени из числа а называется такое число, п – я степень которого равна а)
14.Дайте определение арифметического корня п – й степени из неотрицательного числа(арифметическим корнем п – й степени из неотрицательного числа, называется неотрицательное число, п – я степень которого равна а.
9 класс Тема 3 Уравнения и неравенства с одной переменной. Алгебра
1.Какое уравнение с одной переменной называется целым ( целым уравнением с одной переменной называется уравнение, левая и правая части которого - целые выражения)
2. Как найти степень целого уравнения :
а) если уравнение с одной переменной записано в виде многочлена стандартного вида , то степень этого многочлена называют степенью уравнения.
б) степенью произвольного целого уравнения называют степень равносильного ему уравнения , представляющегося собой многочлен стандартного вида)
3.Дайте определение биквадратного уравнения ( уравнение вида 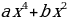 + c = 0, где
+ c = 0, где 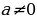 являющемся квадратным относительно
являющемся квадратным относительно 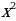 , называется биквадратным уравнением).
, называется биквадратным уравнением).
4. Какое уравнение называется дробным рациональным ( дробным рациональным уравнением называется уравнение, обе части которого являются рациональными выражениями, причём хотя бы одно из них – дробным выражением).
5.Дать определение неравенства второй степени с одной переменной ( неравенства вида 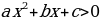
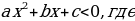 xпеременная,
xпеременная, 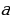 ,b и cнекоторые числа и
,b и cнекоторые числа и 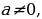
Называют неравенствами второй степени с одной переменной )
6. Алгоритм решения неравенств вида 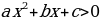
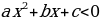 :
:
а) находят дискриминант квадратного трёхчлена 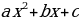 и выясняют, имеет ли трёхчлен корни;
и выясняют, имеет ли трёхчлен корни;
б) если трёхчлен имеет корни , то отмечают их на оси х и через отмеченные точки проводят схематически параболу, ветви которой направлены вверх при 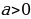 или вниз при
или вниз при 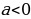 ;
;
если трёхчлен не имеет корней, то схематически изображают параболу, расположенную в верхней полуплоскости при 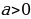 или в нижней при
или в нижней при 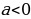 ;
;
в) находят на оси х промежутки, для которых точки параболы расположены выше оси х ( если ре-шают неравенство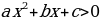 ) или ниже оси х (если решают неравенство
) или ниже оси х (если решают неравенство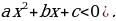
7.На примере неравенства ( х -5) (х + 7) ( х + 9)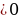 расскажите, как решают неравенства методом интервалов
расскажите, как решают неравенства методом интервалов
9 класс Тема 4 Уравнения и неравенства с двумя переменными. Алгебра
1.Что называется решением уравнения с двумя переменными (решением уравнения с двумя переменными называется пара значений переменных , обращающая это уравнение в верное равенство).
2. Что называется графиком уравнения с двумя переменными (графиком уравнения с двумя переменными множество точек координатной плоскости, координаты которых обращают уравнение в верное равенство).
3. Объясните на примере , как решают систему двух уравнений с двумя переменными, составленную из одного уравнения второй степени и одного уравнения первой степени ( для этого поступают следующим образом:
1)выражают из уравнения первой степени одну переменную через другую;
2)подставляют полученное выражение в уравнение второй степени, в результате чего приводят к уравнению с одной переменной;
3) решают получившееся уравнение с одной переменной;
4)находят соответствующие значения второй переменной .)
4. Что называется решением неравенства с двумя переменными (решением неравенства с двумя переменными называется пара значений этих переменных, обращающая данное неравенство в верное числовое неравенство)
5.Какую пару чисел называют решением системы неравенств с двумя переменными (решением системы неравенств с двумя переменными (пару чисел , которые являются решением как первого, так и второго неравенства системы , т.е. является общим решением этой системы, называют решением системы неравенств с двумя переменными )
6. Изобразите на координатной плоскости множество решений неравенств: а)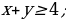 б)
б) 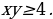
7. Изобразите на координатной плоскости множество решений системы неравенств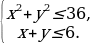
9 класс Тема 5 Арифметическая и геометрическая прогрессии Алгебра
1.Приведите пример последовательности , заданной: а) формулой n- го члена; б) рекуррентной. Найдите пять первых членов этой последовательности. ( а) 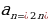 , б)
, б) 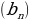 –последовательность.
–последовательность. 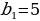 ,
, 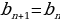 + 5 )
+ 5 )
2.Сформулируйте определение арифметической прогрессии. Какое число называют разностью арифметической прогрессии.? ( арифметической прогрессией называется последовательность, каждый член которой , начиная со второго, равен предыдущему члену, сложенному с одним и тем же числом. Разность между любым её членом, начиная со второго, и предыдущим равна 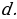 (
(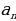 ) – арифметическая прогрессия,
) – арифметическая прогрессия, 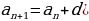 . Число
. Число 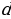 называют разностью арифметической прогрессии).
называют разностью арифметической прогрессии).
3.Как выражается любой член арифметической прогрессии, начиная со второго, через предыдущий и последующий члены ? ( каждый член арифметической прогрессии, начиная со второго, равен среднему арифметическому предыдущего и последующего членов)
4.Обратное утверждение ( если в последовательности (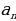 ) каждый член , начиная со второго, равен среднему арифметическому предыдущего и последующего членов , то эта последовательность является арифметической прогрессией)
) каждый член , начиная со второго, равен среднему арифметическому предыдущего и последующего членов , то эта последовательность является арифметической прогрессией)
5. Запишите формулу n- го члена арифметической прогрессии ( 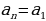 + d (n-1)) 6. Запишите формулы суммы первых n членов арифметической прогрессии (
+ d (n-1)) 6. Запишите формулы суммы первых n членов арифметической прогрессии ( 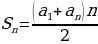 ,
, 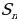 =
=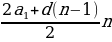 .)
.)
7.Сформулируйте определение геометрической прогрессии. Что называют знаменателем геометрической прогрессии? ( геометрической прогрессией называется последовательность отличных от нуля чисел, каждый член которой, начиная со второго, равен предыдущему члену, умноженному на одно и тоже число. Отношение любого члена последовательности , начиная со второго, к предыдущему члену равно q. Число q называют знаменателем геометрической прогрессии)
8.Как выражается квадрат любого члена геометрической прогрессии, начиная со второго, через предыдущий и последующий члены? (квадрат любого члена геометрической прогрессии, начиная со второго, равен произведению предыдущего и последующего её членов)
9.Обратное утверждение ( если в последовательности чисел, отличных от нуля, квадрат каждого члена, начиная со второго, равен произведению предыдущего и последующего членов, то эта последовательность является геометрической прогрессией).
10. Запишите формулу n- го члена геометрической прогрессии (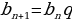 ,
, 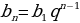 )
)
11. Запишите формулы суммы первых n членов геометрической прогрессии ( 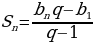 ,
, 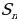 =
=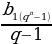 .)
.)
9 класс Тема 6 Элементы комбинаторики и теории вероятностей Алгебра
1.Объясните, как ведётся подсчёт числа возможных вариантов с помощью комбинаторного правила умножения ( пусть имеется n элементов и требуется выбрать из них один за другим k элементов. Если первый элемент можно выбрать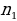 способами, после чего второй элемент можно выбрать
способами, после чего второй элемент можно выбрать 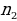 способами из оставшихся, затем третий элемент можно выбрать
способами из оставшихся, затем третий элемент можно выбрать 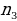 способами из оставшихся и т.д., то число способов , которыми могут быть выбраны все k элементов, равно произведению
способами из оставшихся и т.д., то число способов , которыми могут быть выбраны все k элементов, равно произведению 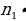
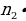
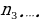
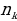 )
)
2. Что означает запись n 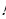 ? Найдите значение выражения
? Найдите значение выражения 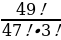 .( 3
.( 3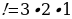 ,
, 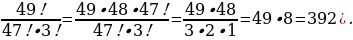
3.Что называется перестановкой из n элементов? Запишите формулу для вычисления числа перестановок из n элементов.( перестановкой из n элементов называется каждое расположение этих элементов в определённом порядке 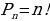 )
)
4. Что называется размещением из n элементов по k ? Запишите формулу для вычисления числа размещений из n элементов по k.( размещением из n элементов по k (k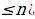 называется любое множество , состоящее из k элементов, взятых в определенном порядке из данных n элементов.)
называется любое множество , состоящее из k элементов, взятых в определенном порядке из данных n элементов.)
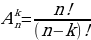
5. Что называется сочетаний из n элементов по k? Запишите формулу для вычисления числа сочетаний из n элементов по k. (сочетаний из n элементов по k называется любое множество , составленное из k элементов, выбранных из данных n элементов.)
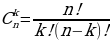
6.Что называется относительной частотой случайного события?( относительной частотой случайного события в серии испытаний называется отношение числа испытаний, в которых это событие наступило, к числу всех испытаний )
7.Как вычисляют вероятность случайного события при классическом подходе?( если все исходы какого-либо испытания равновозможны , то вероятность события в этом испытании равна отношению числа благоприятных для него исходов к числу всех равновозможных исходов)
8.Приведите примеры достоверного события и пример невозможного события Чему равна вероятность достоверного события; невозможного события? (1.Событие , которые при проведении некоторого опыта или наблюдения происходят всегда, называют достоверным событием; вероятность достоверного события равна 1. 2. Событие. которое не может произойти ни при каком исходе опыта или наблюдения, называют невозможным событием; вероятность невозможного события равна 0.)







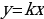 , где х - независимая переменная ,
, где х - независимая переменная , 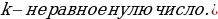
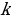 в формуле
в формуле 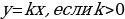 ? ( график прямой пропорциональности расположен в первой и третьей координатных четвертях)
? ( график прямой пропорциональности расположен в первой и третьей координатных четвертях)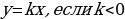 ? ( график прямой пропорциональности расположен во второй и четвертой координатных четвертях)
? ( график прямой пропорциональности расположен во второй и четвертой координатных четвертях)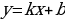 , где x – независимая переменная , k и b – некоторые числа)
, где x – независимая переменная , k и b – некоторые числа)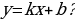 (число
(число 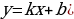
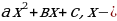 переменная, а, в и с некоторые числа, причём а
переменная, а, в и с некоторые числа, причём а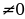 )
)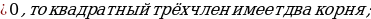
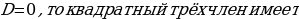 один корень;
один корень; 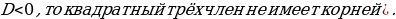
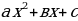 , то
, то 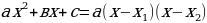 .)
.)
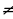 0 )
0 )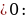
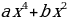 + c = 0, где
+ c = 0, где 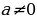 являющемся квадратным относительно
являющемся квадратным относительно 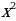 , называется биквадратным уравнением).
, называется биквадратным уравнением). 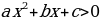
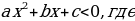 xпеременная,
xпеременная, 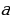 ,b и cнекоторые числа и
,b и cнекоторые числа и 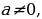
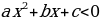 :
: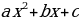 и выясняют, имеет ли трёхчлен корни;
и выясняют, имеет ли трёхчлен корни;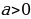 или вниз при
или вниз при 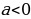 ;
;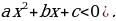
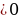 расскажите, как решают неравенства методом интервалов
расскажите, как решают неравенства методом интервалов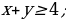 б)
б) 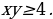
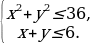
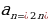 , б)
, б) 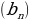 –последовательность.
–последовательность. 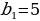 ,
, 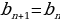 + 5 )
+ 5 )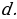 (
(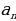 ) – арифметическая прогрессия,
) – арифметическая прогрессия, 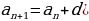 . Число
. Число 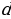 называют разностью арифметической прогрессии).
называют разностью арифметической прогрессии).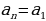 + d (n-1)) 6. Запишите формулы суммы первых n членов арифметической прогрессии (
+ d (n-1)) 6. Запишите формулы суммы первых n членов арифметической прогрессии ( 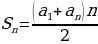 ,
, 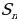 =
=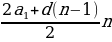 .)
.)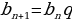 ,
, 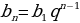 )
)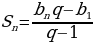 ,
, 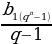 .)
.)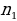 способами, после чего второй элемент можно выбрать
способами, после чего второй элемент можно выбрать 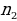 способами из оставшихся, затем третий элемент можно выбрать
способами из оставшихся, затем третий элемент можно выбрать 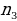 способами из оставшихся и т.д., то число способов , которыми могут быть выбраны все k элементов, равно произведению
способами из оставшихся и т.д., то число способов , которыми могут быть выбраны все k элементов, равно произведению 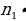
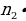
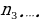
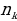 )
)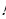 ? Найдите значение выражения
? Найдите значение выражения 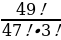 .( 3
.( 3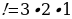 ,
, 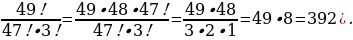
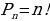 )
)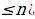 называется любое множество , состоящее из k элементов, взятых в определенном порядке из данных n элементов.)
называется любое множество , состоящее из k элементов, взятых в определенном порядке из данных n элементов.)