Раздел 3. Функции, их свойства и графики. Применение свойств и графиков функций при решении уравнений и неравенств.
Тема 3.13. Логарифмические неравенства
ПАСПОРТ ЗАНЯТИЯ
1. Цели занятия
Методическая цель изучить:
1. Логарифмические неравенства. Основные приемы их решений.
2. Использование свойств и графиков логарифмической функции при решении логарифмических неравенств.
3. Решение логарифмических неравенств по известным алгоритмам.
4. Применение решений логарифмических неравенств в медицине.
Дидактическая цель:
- создание содержательных и организационных условий по изучению понятий «Логарифмических неравенств»;
- создание содержательных и организационных условий по изучению основных приемов решений логарифмических неравенств;
- организация деятельности обучающихся для использования свойств и графиков логарифмической функции при решении логарифмических неравенств;
- организация деятельности обучающихся для решения логарифмических неравенств по известным алгоритмам.
Развивающая цель:
- развитие навыка по применению алгоритма решения логарифмических неравенств;
- развитие умения по нахождению ошибок в преобразованиях и вычислениях.
Воспитательная цель:
- воспитывать умение работать в коллективе;
- воспитывать серьезное отношение к учебному труду, интереса к математике.
2. Тип учебного занятия: изучения и первичного закрепления новых знаний и способов деятельности.
3. Форма учебного занятия: комбинированный урок.
4. Вид занятия – теоретическое.
5. Используемые педагогические технологии: беседа, фронтальная работа, самостоятельная работа.
Формируемые результаты
Предметные:
Знать: понятия «Логарифмических неравенств»; знать основные приемы решения логарифмических неравенств.
Уметь: решать логарифмические неравенства по известным алгоритмам.
Личностные: формировать целостное мировоззрение, соответствующее современному уровню развития науки и общественной практики.
Метапредметные: формировать умение видеть математическую задачу в контексте проблемной ситуации в других дисциплинах, в окружающей жизни.
Методы обучения: учебно – дидактический.
Время проведения занятия 90 минут.
КАРТА ОСНАЩЕНИЯ ЗАНЯТИЯ
Техническое оснащение: оборудование и приборы для демонстраций: мультимедиа проектор, экран, презентация.
Материальное оснащение: доска.
Методическое оснащение: РП ОД.03, КТП ОД.03, технологическая карта, методическая разработка лекционного материала.
ТЕХНОЛОГИЧЕСКАЯ КАРТА ЗАНЯТИЯ
| Этап занятия | Время | Содержание занятия | Деятельность преподавателя | Деятельность обучающихся |
| I. Организационный момент. | 2 мин | Эмоциональ-ный настрой и готовность преподавателя и обучающихся на урок. | Проверка состояния кабинета к занятию проверка внешнего вида обучающихся фиксация отсутствующих | Организацион-ная подготовка к занятию |
| II. Актуализация опорных знаний Фронтальная работа (проверка домашнего задания). | 10 мин
| Фронтальный опрос | Проводит фронтальный опрос – беседу, корректирует и уточняет знания студентов. | Интерактивная деятельность обучающихся |
| III. Изучение нового материала. (Формирование новых знаний и умений)
| 65 мин | Работа по теме занятия в соответствии с формой занятия и технологией проведения | Проверяет и контролирует сформированные знания | Интерактивная деятельность обучающихся |
| IV. Итог занятия. Ответы на вопросы. Рефлексия
| 10 мин | Обобщение пройденного материала, выставление оценок с учетом активности в выполнении заданий | Формирование положительного настроя обучающихся, выставление оценок, подведение итогов | Участвуют в подведении итогов |
| V. Домашнее задание. (Задание к следующему занятию) | 3 мин |
| Пояснения по выполнению домашнего задания | Фиксация домашнего задания |
ПЛАН-КОНСПЕКТ УЧЕБНОГО ЗАНЯТИЯ
I. Организационный момент.
II. Актуализация опорных знаний. Фронтальная работа (проверка домашнего задания).
III. Изучение нового материала (Формирование новых знаний и умений).
1. Логарифмические неравенства. Основные приемы их решений.
2. Использование свойств и графиков логарифмической функции при решении логарифмических неравенств.
3. Решение логарифмических неравенств по известным алгоритмам.
4. Применение решений логарифмических неравенств в медицине.
IV. Итог занятия. Ответы на вопросы. Рефлексия.
V. Домашнее задание.
СПИСОК ИНФОРМАЦИОННЫХ ИСТОЧНИКОВ
Для обучающихся:
1. Лекционный материал.
2. Дидактический материал.
3. Алгебра и начала математического анализа. 10-11 классы: учеб. Для общеобразоват. организаций: базовый уровень /Ш.А. Алимов и др. – 19-е изд. – М.: Просвещение.
Для преподавателя:
1. Алгебра и начала математического анализа. 10-11 классы: учеб. Для общеобразоват. организаций: базовый уровень /Ш.А. Алимов и др. – 19-е изд. – М.: Просвещение.
2. Интернет-ресурсы:
https://urok.1sept.ru/articles/638109
https://resh.edu.ru/subject/lesson/3852/conspect/199118/
ХОД ЗАНЯТИЯ
I. Организационный момент.
Эмоциональный настрой и готовность преподавателя и обучающихся на урок. Сообщение темы занятия. Целеполагание на занятие совместно с обучающимися, обсуждение и постановка задач.
II. Актуализация опорных знаний.
Фронтальная работа (проверка домашнего задания):
III. Изучение нового материала (Формирование новых знаний и умений).
1. Логарифмические неравенства. Основные приемы их решений.
Определение: неравенство, содержащее переменную только под знаком логарифма, называется логарифмическим.
Решение логарифмического неравенства основано на том, что функция у = logаx при а 0 является монотонно возрастающей, а при 0 a
1) Решение простейших логарифмических неравенств.
Простейшее логарифмическое неравенство имеет вид: logаx (
Чтобы решить простейшее логарифмическое неравенство, нужно:
1. Записать ОДЗ: 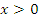
2. В правой части неравенства с умножить на logаа
3. Сравнить основание логарифма с единицей.
4. Сравнить выражения, стоящие под знаком логарифма.
5. Решить систему неравенств.
6. Записать ответ.
Пример №1. Решите неравенство 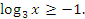
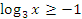
ОДЗ: 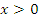
Совет: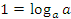
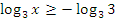
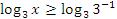
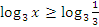
Так как основание больше 1, знак неравенства не меняется 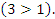
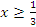
С учетом ОДЗ: 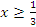
Ответ: 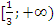
Пример №2. Решите неравенство 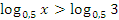 .
.
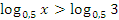
ОДЗ: 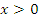
Так как основание меньше 1, знак неравенства меняется 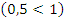 .
.
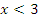
Учтем ОДЗ: 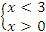
Ответ: 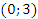
2) Решение логарифмических неравенств, сводящихся к простейшим
Если логарифмическое неравенство имеет вид: logаf(x) (то для его решения нужно:
1. Найти область определения функции f(x) 0
2. В правой части неравенства с умножить на logаа
3. Сравнить основание логарифма с единицей.
4. Сравнить выражения, стоящие под знаком логарифма.
5. Решить систему неравенств.
6. Записать ответ.
Пример №3. Решите неравенство 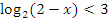 .
.
ОДЗ: 
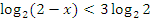
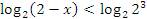
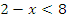
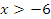
Ответ: 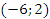
Фронтальная работа с группой. Закрепление изученного. Решение упражнений по учебнику.
3) Решение логарифмических неравенств вида logаf(x) logаg(x).
Алгоритм решения:
1. Найти область определения каждой функции.
2. Привести неравенство к виду logаf(x) logаg(x).
3. Сравнить основание логарифма с единицей.
4. Сравнить выражения, стоящие под знаком логарифма.
5. Решить систему неравенств.
6. Записать ответ.
Пример №4. Решите неравенство 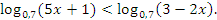
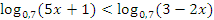
ОДЗ:
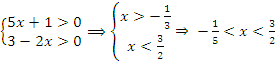
Так как основание меньше 1, знак неравенства меняется 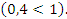
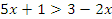
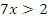
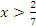
Ответ: 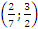
Фронтальная работа с группой. Закрепление изученного. Решение упражнений по учебнику.
4) Решение логарифмических неравенств с использованием свойств логарифмов
Пример №5. Решите неравенство: 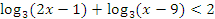 .
.
ОДЗ: 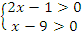
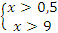
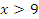
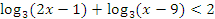
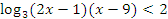
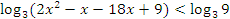

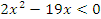

Ответ: 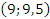
3. Решение логарифмических неравенств по известным алгоритмам.
Фронтальная работа с группой. Закрепление изученного. Решение упражнений по учебнику.
IV. Итог занятия. Ответы на вопросы. Рефлексия.
V. Домашнее задание.
1) Изучите лекционный материал.
2) Прочитайте учебник Алгебра и начала математического анализа. 10-11 классы: учеб. Для общеобразоват. организаций: базовый уровень /Ш.А. Алимов и др. – 19-е изд. – М.: Просвещение. Изучите стр.109-111.
3) Повторите темы «Иррациональные уравнения», «Иррациональные неравенства», «Показательные уравнения», «Показательные неравенства», «Логарифмические уравнения».
10