ГОСУДАРСТВЕННОЕ АВТОНОМНОЕ ОБРАЗОВАТЕЛЬНОЕ
УЧРЕЖДЕНИЕ СРЕДНЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
НОВОСИБИРСКОЙ ОБЛАСТИ
«БАРАБИНСКИЙ МЕДИЦИНСКИЙ КОЛЛЕДЖ»
МЕТОДИЧЕСКАЯ РАЗРАБОТКА
КОМБИНИРОВАННОГО ЗАНЯТИЯ ДЛЯ ПРЕПОДАВАТЕЛЯ
ДИСЦИПЛИНА «МАТЕМАТИКА»
Раздел 1. Математический анализ
Тема 1.1. Значение математики в профессиональной деятельности.
Решение уравнений.
Специальность
31.02.01 Лечебное дело
Курс – первый
2015
| Одобрена на заседании цикловой
методической комиссии _________________ Протокол №___от_______________________ Председатель___________________________
Разработчик: О.А. Потемкина
|
Оглавление
Выписка из рабочей программы дисциплины «Математика» для специальности 31.02.01 Лечебное дело 4
Методический лист 5
Примерная хронокарта занятия 6
Мотивация 7
Приложение 1 8
Актуализация опорных знаний 8
Приложение 2 18
Задания для закрепления 18
Приложение 3 21
Контролирующий материал по теме «Значение математики в профессиональной деятельности. Решение уравнений» 21
Эталоны ответов к контролирующему материалу по теме «Значение математики в профессиональной деятельности. Решение уравнений» 21
Критерии оценки 21
Выписка из рабочей программы
дисциплины «Математика»
для специальности 31.02.01 Лечебное дело
| Наименование разделов и тем | Содержание учебного материала, лабораторные и практические работы, самостоятельная работа обучающихся, курсовая работа (проект) | Объем часов | Уровень освоения |
| 1 | 2 | 3 | 4 |
| Раздел 1. | Математический анализ | 45 |
|
| Тема 1.1. Значение математики в профессиональной деятельности. Решение уравнений. | Содержание учебного материала | 2 |
|
|
| Роль и место математики в современном мире. Решение уравнений. |
| 1,2 |
| Лабораторные работы | ‑ |
|
| Практические занятия | ‑ |
| Контрольные работы | ‑ |
| Самостоятельная работа обучающихся Работа с учебным материалом, составление конспекта, выполнение упражнений, решение прикладных задач. Ответы на вопросы [1, стр. 16] | 1 |
Методический лист
Вид занятия – комбинированное занятие
Продолжительность – 90 мин.
Требования к результатам освоения темы в соответствии с ФГОС по специальности среднего профессионального образования 060101 Лечебное дело:
В результате изучения темы обучающийся должен уметь:
– решать прикладные задачи в области профессиональной деятельности;
В результате изучения темы обучающийся должен знать:
– значение математики в профессиональной деятельности и при освоении профессиональной образовательной программы;
Цели занятия:
1. Учебные цели:
2. Развивающие цели:
способствовать
формированию умений применять приемы сравнения, обобщения, выделения главного;
развитию математического кругозора, мышления и речи, внимания и памяти.
3. Воспитательные цели: способствовать формированию культуры общения, внимания, интереса к предмету, способствовать пониманию студентом сущности и социальной значимости своей будущей профессии, проявления к ней устойчивого интереса.
Методы обучения: объяснительно-иллюстративный, репродуктивный.
Место проведения занятия: аудитория колледжа.
Интегративные связи: физика, геометрия и все предметы, где используется математический аппарат
Список используемых источников:
Гилярова, М. Г. Математика для медицинских колледжей [Текст]. – Ростов н/Д: Феникс, 2011. – 410 с. – (Медицина)
Михеев, В.С. Математика: учеб. пособие [Текст] / В.С. Михеев [и др.]; под ред. Н.М. Демина. –Ростов н/Д : Феникс, 2009. – 896 с. – (Среднее профессиональное образование).
Оснащение занятия:
Доска
Раздаточный материал
Проектор
Мультимедиа
Домашнее задание:
Повторение материала по конспектам теоретического занятия
Ответы на вопросы [1, стр. 16]
Примерная хронокарта занятия
| № | Наименование этапа | Время | Цель этапа | Деятельность | Оснащение |
| преподавателя | студентов |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Организационный этап | 1 | Организация начала занятия. Проверка посещаемости и внешнего вида студентов. Сообщение темы и плана занятия. | Отмечает отсутствующих студентов в журнале. Сообщает тему и план занятия. | Староста называет отсутствующих студентов. | Журнал |
| Мотивационный этап | 2 | Развитие интереса к дисциплине | Объясняет студентам важность изучения данной темы | Слушают, задают вопросы | МР Приложение 2 |
| Цели занятия | 1 | Установка приоритетов при изучении темы | Озвучивает цели занятия | Слушают, записывают в дневник новую тему | Методический лист МР |
| Актуализация опорных знаний | 45 | Ориентация на глубину усвоения знаний, систематизация материала. Развитие математического кругозора, мышления и речи, внимания и памяти. | Актуализирует знания студентов за курс математики средней школы | ,Организуют диалог с преподавателем, решают задачи | Приложение 1 |
| Выполнение заданий для закрепления знаний | 25 | Закрепление и осмысление знаний формированию умений применять приемы сравнения, обобщения, выделения главного. | Инструктирует и контролирует выполнение заданий, обсуждает правильность ответов | Выполняют задания, слушают правильные ответы после выполнения, вносят коррективы | Приложение 2 |
| Предварительный контроль знаний | 14 | Оценка эффективности занятия и выявление недостатков в знаниях | Инструктирует и проводит контроль | Выполняют задания | Приложение 3 |
| Задание для самостоятельной внеаудиторной работы студентов | 1 | Формирование и закрепление знаний | Дает задание для самостоятельной внеаудиторной работы студентов, инструктирует о правильности выполнения | Записывают задание | Методический лист МР |
| Подведение итогов занятия | 1 | Подведение итога занятия | Выставляет оценки, дав комментирий. | Слушают, обсуждают, анализируют. | Журнал |
Слайд 1
Мотивация
Подготовка высококвалифицированных специалистов, конкурентоспособных на рынке труда, компетентных, ответственных, свободно владеющих своей профессией и ориентированных в смежных областях деятельности, способных к профессиональному росту и профессиональной мобильности в условиях информатизации общества и развития новых наукоемких технологий, является одной из основных задач образования. Учитывая, что среднее профессиональное образование является одной из важнейших составляющих современного образовательного пространства РФ, в значительной мере влияющего на развитие инновационной экономики страны, решение указанной задачи применительно к подготовке специалистов в учреждениях среднего профессионального образования приобретает особую значимость.
Математика принадлежит к числу тех дисциплин общеобразовательного блока, которые имеют большие возможности для развития личности. В силу специфики своего содержания данный учебный предмет формирует способность к усвоению новой информации, умение планировать и адекватно оценивать свои действия, развивает силу и гибкость ума, способность к аргументации и другие качества, необходимые современному специалисту.
Приложение 1 Актуализация опорных знаний
Слайд 2-3
1. Алгебраические уравнения
Дробно-рациональные уравнения
Рациональным уравнением называется уравнение вида
(*)
где x – неизвестная величина, Р(х), Q(x), F(x), R(x) – многочлены, содержащие неизвестную х, причем Q(x)≠ 0;R(x)≠ 0.
Решение.
Уравнение (*) – это пропорция, известная из математики 6 класса, которая записывается как или а : b = с :d.
По главному свойству пропорции произведение крайних (средних) членов пропорции равно произведению средних (крайних) ее членов, т.е.
a·d=b·с или b·с = a·d.
Запишем далее это свойство для уравнения (*):
P(x)·R(x) = Q(x)·F(x). (**)
Слайд 4
Уравнение (**) после соответствующих преобразований может стать одним из следующих:
I. ах + b = 0 – линейное уравнение 1-й степени.
Его решение
ах = -b – при
Слайд 5
II. ах2 + bx + c = 0 – уравнение 2-й степени, или квадратное уравнение.
Для решения таких уравнений будем пользоваться формулой, которую вывел французский математик Франсуа Виет:
где D = b2 – 4ас – дискриминант квадратного уравнения.
Возможные варианты при решении квадратных уравнений
1. D 0 – уравнение II имеет два различных корня, выраженных действительными числами.
2. D =0 – уравнение II имеет один корень.
3. D 0 – уравнение II имеет два корня, выраженных комплексными числами:
;
где
Примечания.
1. Если в уравнении II а = 1, то такое уравнение называется приведенным квадратным уравнением, его принято записывать в виде
x2 + px + q = 0. II'
Если D ≥ 0 и корни выражаются целыми числами, то его принято решать по 2-й формуле Виета, согласно которой:
x1 · х2 =q;
х1 + х2=–р.
2. Уравнение ах2 + bx + c = 0 приводится к приведенному путем деления на а его правой и левой части, т.е.:
ах2 +bx + c = 0 (:a) =
х2 + px + q = 0. II”
Сравнивая уравнения II' и II”, видим, что
Слайд 6
3. Выражение у = ах2 +bх + с называется квадратным трехчленом.
D = b2 – 4ас – дискриминант квадратного трехчлена.
Пусть х1 и х2 – значения переменных в квадратном трехчлене, при которых он обращается в нуль. Это корни трехчлена.
В этом случае, как показал немецкий математик Карл Вейерштрасс (XIX веке), квадратный трехчлен можно разложить на множители:
у = ах2 +bx + c = a·(x – xl)(x – x2), если D≠0,
у = ах2 +bх + с = а·(х – х1) , если D = 0.
Эти формулы называются формулами разложения квадратного трехчлена на множители.
III. ах3 +bx2 +cx + d = 0 – уравнение третьей степени, или кубическое уравнение.
IV. ах4 + bх3 + сх2 + dx + е = 0 – уравнение четвертой степени.
Кубические уравнения и уравнения четвертой степени решаются по сложным формулам, которые вывел итальянский математик Кордано (XVII век), они даны в справочниках по математике.
V. ахn +bхп-1 +схn-2 +...+ т = 0, где п = 5,6,7, ...,к.
Это уравнение n-й степени.
Общей формулы для нахождения корней уравнения выше четвертой степени не существует, и, как доказали французский математик Эварист Галуа (1811-1832) и выдающийся норвежский математик Нильс Абель (1802-1829), уравнения этого класса разрешить невозможно.
Как правило, такие уравнения решаются на компьютерах; можно некоторые из них решить и без ПК, применяя специальные приемы.
Слайд 7
VI. ax4 + bx2 +с = 0.
Это частный случай уравнения IV, и называется оно биквадратным.
Решение:
Пусть х2 = у , и тогда получаем ау2 +bу + с = 0 =
, где D = b2 – 4ас
VII. ахn +b = 0 – двучленное уравнение n-й степени.
Разделив его на а и обозначив , получим , с0.
Для решения этого уравнения достаточно найти корни уравнения уn= ±1 и умножить каждое из них на.
Примеры решения алгебраических уравнений
Слайд 8
Пример 1.
Найдем область допустимых значений данного уравнения (ОДЗУ). Очевидно, что х≠2 и х ≠0. Это ограничения на решения (корни) данного уравнения.
Далее воспользуемся свойством пропорции, уравнение (1) примет вид
(2х – 3)· х = (х + 2)·(2х + 5);
2х2 –3х = 2х2 + 5х + 4х + 10;
2х2 – 3x – 2х2 – 9x + 10=0;
–12x – 10=0 [:(–2);
6x + 5=0;
6х = -5;
Ответ:
Слайд 9
Пример 2.
Преобразуем его так:
| ; ОДЗУ: x ≠ 5 и x ≠ –1 | (2') |
Далее воспользуемся свойством пропорции, уравнение (2') примет вид
(3х + 2)·(х + 1) = (х-5)(3х-4);
3x2 + 3х + 2х + 2 = 3х2 – 4х –15х + 20;
3х2 + 5х + 2 – 3х2 + 9х – 20= 0;
24х – 18=0 [: (6);
4х – 3 = 0;
4х = 3;
;
х = 0,75.
Ответ: .
Слайд 10
Пример 3.
; ОДЗУ: х ≠0 и х≠4.
Используя основное свойство пропорции, имеем
х·х = 2х + 8;
х2 – 2х – 8 = 0;
D = 36; ;
Ответ: {- 2; 4}.
Слайд 11
Пример 4.
; ОДЗУ: х≠0
Далее по свойству пропорции имеем:
(2x–3)·x = 2;
2х2 – 3x = 2;
2x2 –3x –2 = 0;
а = 2; b = –3; D = b2 – 4ac;
D = 32 – 4·2·(-2) = 9 + 16 = 25; ;
Слайд 12
Пример 5.
2x2 + x – 8 = 0;
а = 2; b=1; с = –8;
D = b2 – 4ас = 1 + 4·2·8 = 65;
Ответ:
2. Уравнения с неизвестной под знаком модуля
Слайд 13-14
Рассмотрим уравнения, содержащие неизвестную величину под знаком модуля в правой или левой его частях, или в правой и левой частях одновременно.
Например:
При решении таких уравнений применяют следующие методы:
раскрытие модуля по определению –
возведение обеих частей уравнения в квадрат;
метод разделения на промежутки (интервалы).
Слайд 15
Пример 1.
Решить уравнение .
1-й способ решения (раскрытие модуля по определению).
Так как по определению
то данное уравнение равносильно следующей совокупности двух смешанных систем:
Из первой системы этой совокупности находим x1 = 4,
из второй х2 = – 1.
Ответ: {4; –1}
Слайд 16
Пример 2.
Решить уравнение: |x+4|=2x-10.
2-й способ решения (возведение обеих частей уравнения в квадрат).
Для того, чтобы решить уравнение содержащее модуль, необходимо освободиться от знака модуля. Для этого следует: возвести в квадрат обе части уравнения, решить его. Но не забывать, что при возведении в квадрат появляются лишние корни, поэтому, надо найти ОДЗ и выявить принадлежат ли корни данному условию.
| Решение: | ОДЗ: |
| (|x+4|)2=(2x–10)2 x2 +8x+16=4x2 –40x+100 3x2 –48x+84=0 /3 x2 –16x+28=0 x1=14, x2=2 | 2x-10 0; 0; 2x 10 ; 10 ; x 5. 5.
|
x1=14  [5;+
[5;+  ), х2=2
), х2=2  [5;+
[5;+  )
)
Ответ:14
Слайд 17-18
Пример 3.
Решите уравнение: |5-2x|+|x+3|=2-3x
3-й способ решения (метод интервалов).
Для того, чтобы решить уравнение, содержащее неизвестную под знаком модуля, необходимо освободиться от знака модуля, используя его определение. Для этого следует:
1) Найти критические точки, т.е. значение неизвестной, при которых выражение, стоящее под знаком модуля, обращается в нуль;
2) Разбить область допустимых значений уравнения на промежутки, на каждом из которых, выражения, стоящие под знаком модуля сохраняют знак;
3) На каждом из этих промежутков уравнение записать без знака модуля, а затем решить его.
Объединение решений, найденных на всех промежутках, и составляет решение исходного уравнения.
5–2x=0; x+3=0
х=2,5; х=–3
| | (- ;-3) | [-3;+2,5) | [-2,5;+ ) |
| 5-2х | + | + | – |
| х+3 | – | + | + |
| (- ;-3) | [-3;+2,5) | [-2,5;+ ) |
| 5 – 2х – х–3 –2+3х=0 0х=0 х–любое число (– ;–3) | 5 – 2x+x+3 – 2+3x=0 2х= – 6 х= –3 [–3;2,5) | 2х – 5+х+3 – 2+3х=0 6х=4 x=2/3 [2,5;+ ) |
(- ;-3) {-3}=(- ;-3]
Ответ: (- ;-3].
3. Иррациональные уравнения
Слайд 19-20
Уравнения, содержащие переменную под знаком одного (или нескольких) корней, называются иррациональными.
Например:
Решение иррациональных уравнений сводится к освобождению их от корней. Предварительно отметим ряд обстоятельств, которые упрощают решение иррациональных уравнений.
Если в иррациональные уравнения входят корни четной степени, то предполагается, что они имеют только арифметические значения, т.е.; в связи с этим замечанием уравнение
решений не имеет, т.к. числовое значение левой части ≥ 3, а по условию примера это ноль.
В процессе освобождения от корней (при возведении в степень) не всегда получаются равносильные уравнения, поэтому не исключено появление посторонних решений (лишних корней).
Следовательно, корни иррациональных уравнений необходимо всегда проверять!
Значения неизвестной, выраженной комплексными числами, из решения исключаются.
Покажем на примерах, как это делается.
Слайд 21
Пример 1.
Ответ: , т.к. левая часть данного уравнения больше или равна 2.
Пример 2.
Решение.
Возводя в квадрат левую и правую часть данного уравнения, получим:
х + 3 = 16 х = 16 – 3 = 13.
Проверка: – верно.
Ответ: {13}
Слайд 22
Пример 3.
Решение.
Переносим в правую часть величину х и, возведя в квадрат обе части полученного уравнения, будем иметь:
Проверка:
– верно;
следовательно,
х = 13 – лишний корень.
Ответ: {6}.
Слайд 23
Пример 4.
Решение.
Можно сразу возводить в квадрат обе части данного уравнения, но поступим так: оставим в левой части один из радикалов (корней), например 2-й, а затем будем возводить в квадрат:
Проверка: – верно.
Ответ: {-1}.
Слайд 24-25
4. Показательные уравнения
Уравнения, содержащие неизвестную в показателе одной или нескольких степеней, называются показательными.
Например:
Рассмотрим наиболее распространенные показательные уравнения.
aF(x)= 1.
Здесь F(x) — многочлен, содержащий неизвестную х, а – основание степени, где а0, а≠1.
Решение. Так как 1 = а°, то имеем: aF(x)= a0 =F(x)= 0.
Получили одно из известных алгебраических уравнений: линейное, квадратное и т.д.
Пример 1.
.
Решение. Так как 1 = 50, то получаем
х1 = –2, х2 = 4.
Слайд 26
aF{x)=b, где b0
Здесь возможны 2 варианта.
| а) b = аk и тогда aF(x) = аk F(x) = k.
| б) b = А, т.е. имеем aF(x) = А. По определению логарифм — это показатель степени, т.е. k = loga А. Подставляя вместо k выражение F(x), получаем F(x)=loga А и из полученного уравнения находим х. |
| Пример 2.
Решение. Так как 9 = 32 , получим
=0 = x1 = 2, х2 = – 4. | Пример 3. . Решение. x = log530. Перейдём к десятичным логарифмам и найдём значение х. Формула перехода: , в качестве с мы взяли число 10. Итак,
|
Слайд 27
3. m · aF(x) + n ·a F(x) = С, где m, n, С – действительные числа.
Решение.
aF(x) (m + n) = С .
Обозначая , получим (см. 2-й тип).
Пример 5.
Решение.
Так как , то
= = =
= = х = 3.
Слайд 28
4. , где т, п, с – действительные числа.
Решение.
Примем , тогда получим квадратное уравнение относительно z:, из которого находятся z1 и z2, а затем значения х1 и х2-
Пример 6.
.
Решение.
Так как , получим .
Пусть , тогда = .
не подходит, т.к. положительное число в любой степени не может стать числом отрицательным. Имеем 3х =9=х = 2.
Слайд 29
Имеем две равные показательные функции, у которых одинаковые основания. Следовательно, показатели F(x) и Q(x) должны быть равными,
т.е. F(x)= Q(x).
Решая это уравнение, получим соответствующие значения х.
Пример 7.
.
Решение. В этом уравнении значение х входит в показатели четырех степеней. Приведем выражение слева и справа к одному основанию а = 10.
Получим:
0,1 = 10-1; 100 =102;,
следовательно, будем иметь: .
При умножении степеней показатели складываются, т.е. получим
Слайд 30
6. , где Q(x) – многочлен относительно х.
Такие уравнения решаются графически.
Пример 8.
.
Справа и слева в этом примере две функции:
– показательная;
– линейная.
Построив их графики в одной системе координат, получим такую картину:

Графики пересекаются в точке: х1 = -1,8; x2 = 2.
Приложение 2 Задания для закрепления
(примерные)
Алгебраические уравнения | Слайд 31-35 |
| 
| 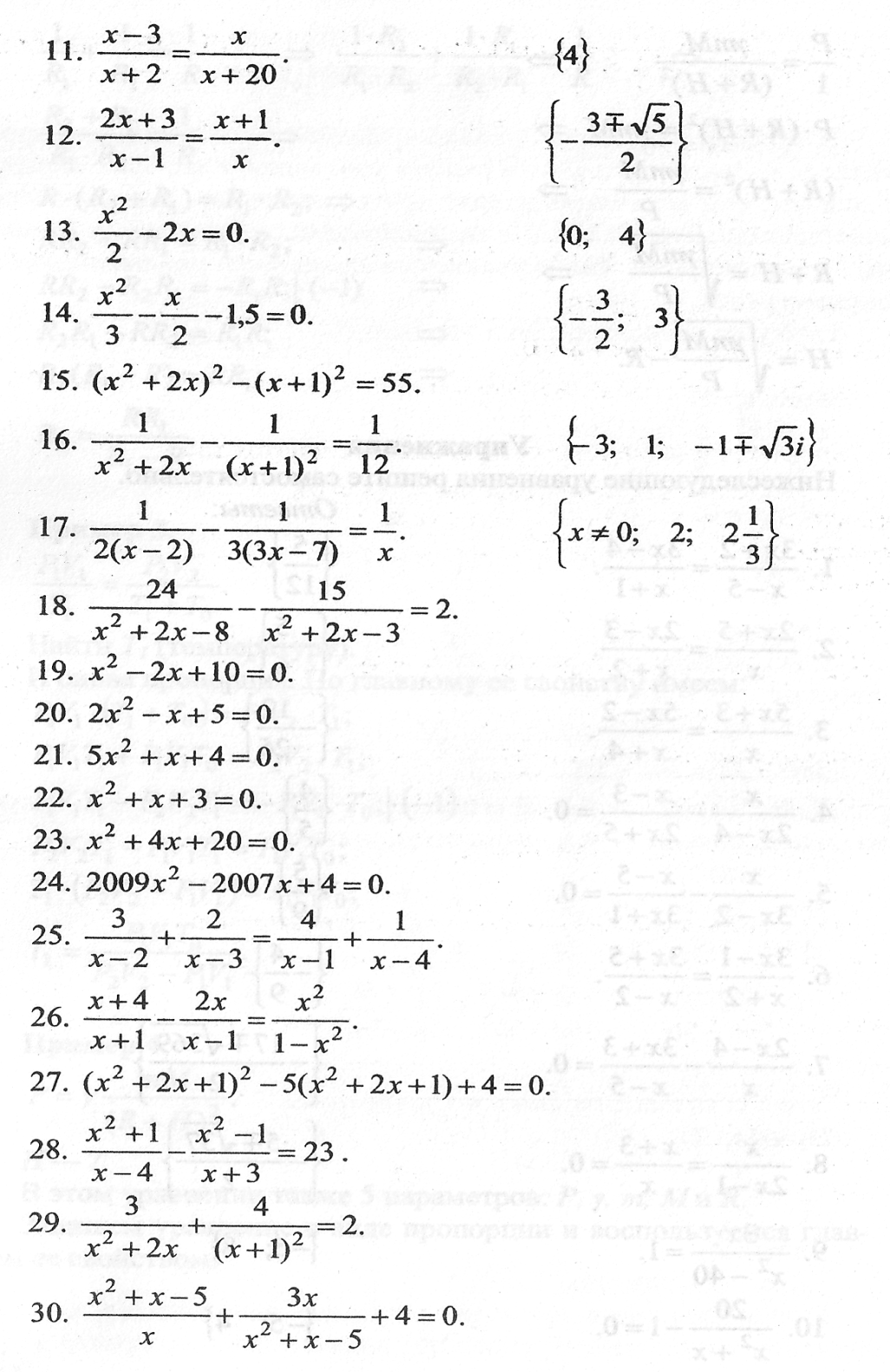
|
Уравнения с неизвестной под знаком модуля Слайд 36 | Иррациональные уравнения Слайд 37 |
| 
| 
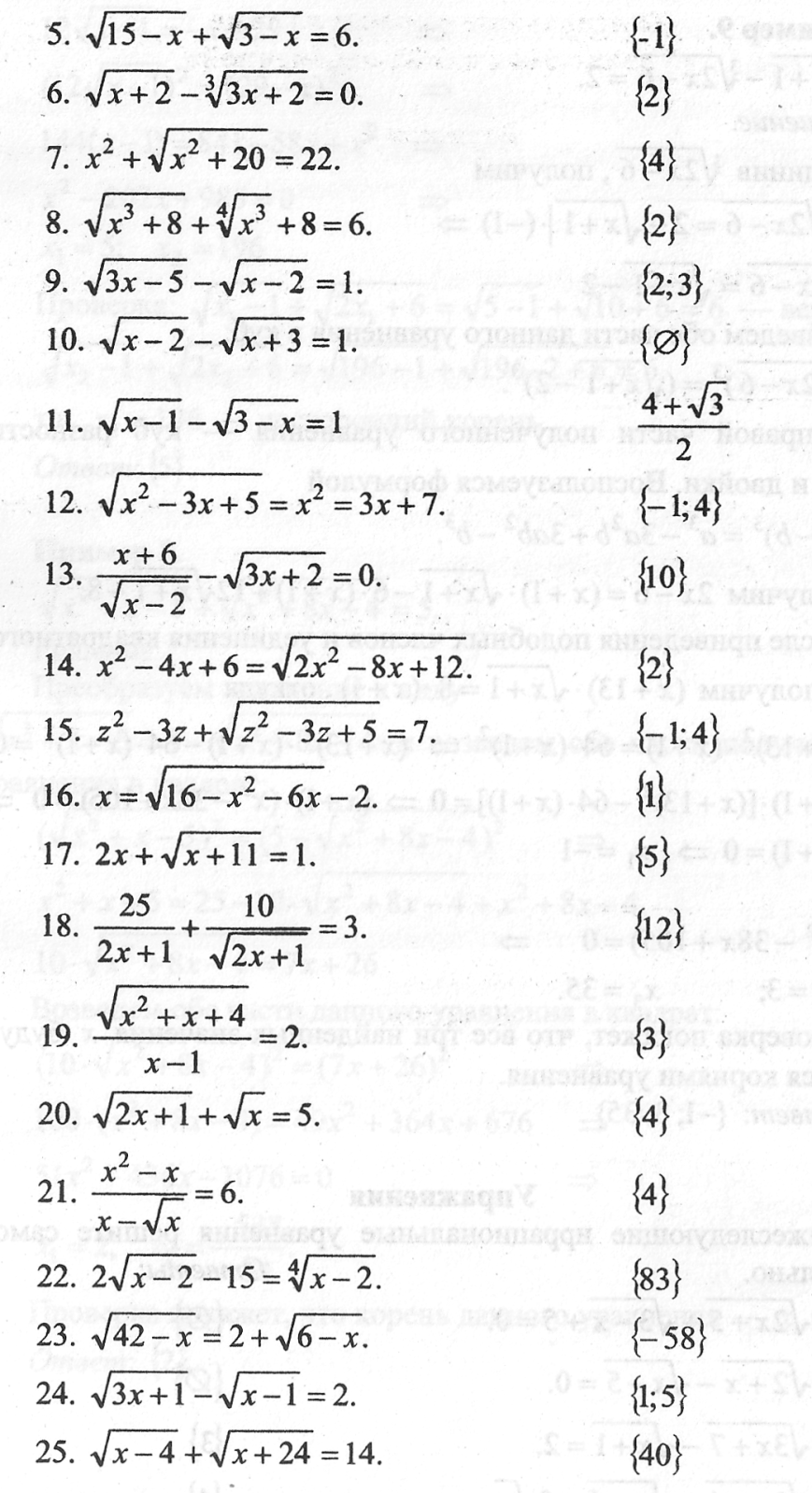
|
Показательные уравнения | Слайд 38-40 |
| 1) 1) 2)  3)  4) 5) 6)  7) 8) 9) 10) 11) 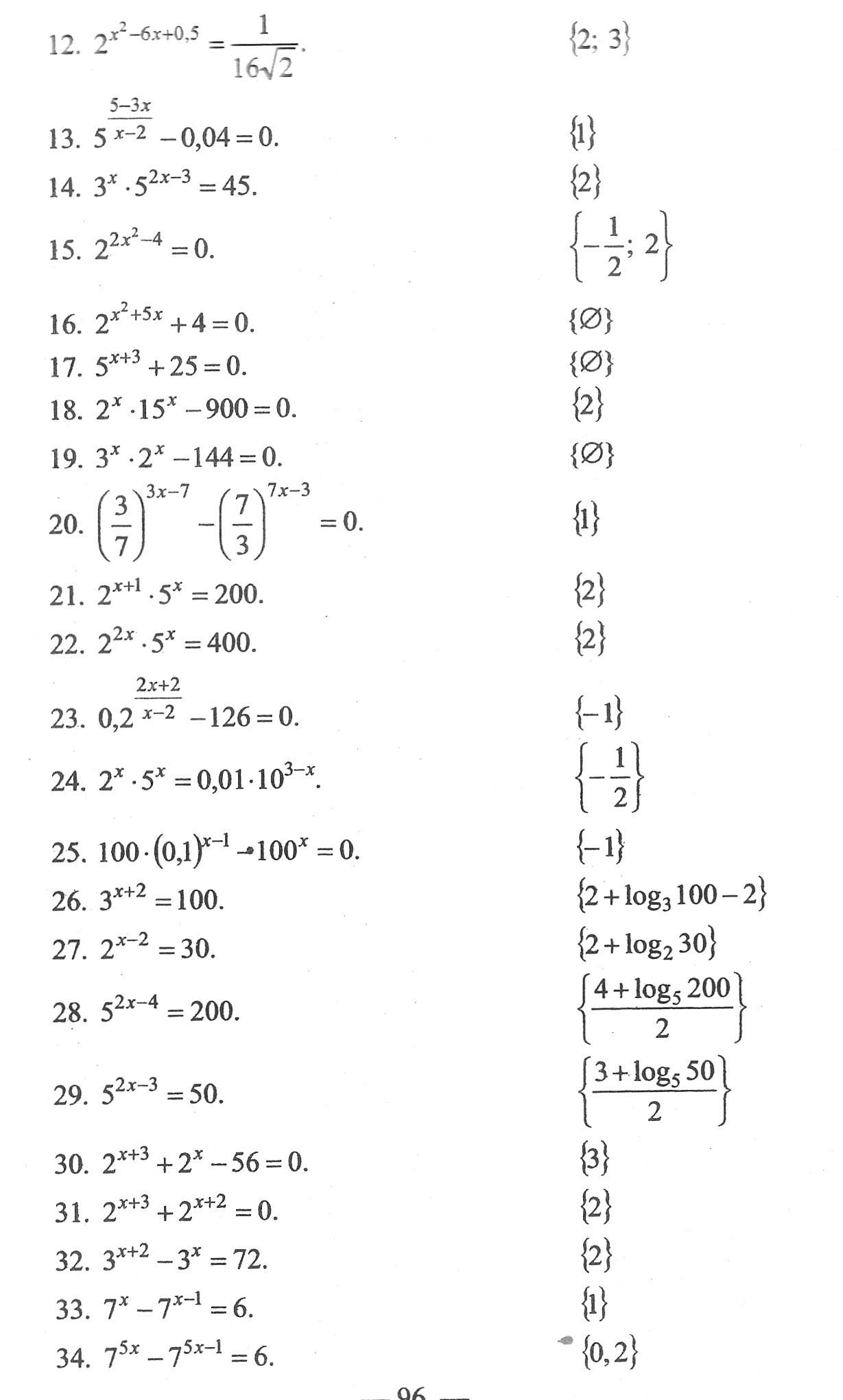 12) 13) 
| 14) 15) 16) 17)  |
|
|
|
Приложение 3 Контролирующий материал по теме
«Значение математики в профессиональной деятельности.
Решение уравнений»
| 1 вариант | 2 вариант |
|
Решите уравнения: =0,04
|
Решите уравнения: =25
|
Эталоны ответов к контролирующему материалу по теме
«Значение математики в профессиональной деятельности.
Решение уравнений»
| 1 вариант | 2 вариант |
|
Решите уравнения: {2} {4} |
Решите уравнения: {1,8 } |
Критерии оценки
«5» – 90-100% (все ответы совпадают или допущена 1 неточность в записи ответа);
«4» – 80% (в двух примерах ответы совпадают или допущены 2 неточности в записи ответа);
«3» – 70% (правильный ответ только в одном примере);
«2» – задание полностью не выполнено.