Научно-исследовательская работа по теме:
Фигурные числа
Оглавление
Введение 3
I.История возникновения фигурных чисел 4
II. Виды фигурных чисел 5
2.1 Классические многоугольные числа 6
2.2 Центрированные полигональные числа 7
2.3 Пространственные фигурные числа 9
III. Значение фигурных чисел в нашей жизни 12
Заключение 14
Список использованной литературы 15
Приложения 15
Введение
Числа окружают нас повсюду. Пифагор сказал: «Числа правят миром». С помощью них не только записывают результаты измерений, сравнивают величины, вычисляют, но даже рисуют картины, проектируют здания, сочиняют музыку, делают выводы. Фигурные числа — числа, которые можно представить с помощью геометрических фигур. Эта историческая концепция восходит к пифагорейцам, которые разработали алгебру на геометрической основе; отголоском этого подхода осталось выражение «возвести число в квадрат или в куб». В теории чисел и комбинаторике фигурные числа связаны со многими другими классами целых чисел - биномиальными коэффициентами, совершенными числами, Мерсенна, Фибоначчи, Люка и других. В своей исследовательской работе я решила рассмотреть историю фигурных чисел, их использование не только в математике, но и в окружающей жизни. В современной науке и практике известно множество видов и типов фигурных чисел. Они используются в молекулярном строении, в пищевых предприятиях, во всех математических областях и т.д.
Цель работы: подробно изучить и исследовать одно из понятий математики – «фигурное число» и выявить его роль в нашей современной жизни.
Задачи работы:
Собрать и проанализировать материал по данной теме;
Рассмотреть историю возникновения фигурных чисел;
Изучить виды фигурных чисел и их свойства;
Представить примеры видов фигурных чисел;
Рассмотреть возможности применения фигурных чисел в повседневной жизни (в живописи, архитектуре, дизайне и других сферах).
Методы исследования:
Изучение и анализ литературы;
Сбор и анализ информации;
Подбор примеров фигурных чисел, в нашей современной жизни.
I.История возникновения фигурных чисел
Фигурные числа использовались еще в V – IV веках до н. э. Пифагор считал, что главная наука о числе - арифметика, неразрывно связана с геометрией и потому числа, соответствующие правильным геометрическим фигурам, назывались фигурными. Древними греками и пифагорейцами числа мыслились зримо, в виде камней, разложенных на песке или на счетной доске – абаке.(Приложение 1,рис.1) По этой причине греки не знали нуля, потому что было невозможно его «увидеть». Но и единица еще не была полноправным числом, а представлялась неким "числовым атомом", из которого образовывались все числа. Пифагорейцы называли единицу "границей между числом и частями", то есть между целыми числами и дробями, но в то же время они видели в ней "семя и вечный корень". Число же представлялось как множество, составленное из единиц. Особое положение единицы как "числового атома", приравнивало ее к точке, считавшейся "геометрическим атомом". Вот почему Аристотель писал: "Точка есть единица, имеющая положение, единица есть точка без положения", то есть Пифагорейские числа в современной терминологии являются натуральными числами. Числа-камешки раскладывались в виде правильных геометрических фигур, эти фигуры были классифицированы. Таким образом, появились цифры, которые сегодня называются фигурными числами.
Древние греки, когда им приходилось умножать числа, рисовали прямоугольники; результатом умножения четырех на семь был прямоугольник со сторонами четыре и семь. Это - развитие счета на камушках. Многие закономерности, связанные с действиями с числами, были обнаружены древнегреческими учеными при изучении рисунков, чертежей. И на протяжении многих веков лучшим способом подтверждения достоверности таких отношений был геометрический метод, с прямоугольниками, квадратами, пирамидами и кубами. В V - IV веках до нашей эры ученые, комбинируя натуральные числа, составляли из них затейливые ряды, придавая элементам этих рядов геометрическое истолкование. С их помощью можно выложить правильные геометрические фигуры: треугольники, квадраты, пирамиды и т.д.
Следовательно, фигурные числа - это общее название чисел, связанных с определенной геометрической фигурой. Предположительно, с понятием фигурного числа связано выражение «возвести число в квадрат или в куб».
II. Виды фигурных чисел
Фигурные цифры сильно отличаются друг от друга. Они могут быть представлены, как просто числами, так и в виде взаимосвязанных различных структур любых объектов. Со времён пифагорейцев традиционно выделяются следующие виды фигурных чисел:
• Линейные числа — числа, которые делятся на единицу и на самих себя, выраженные в виде последовательности точек, выстроенных в линию: 1, 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, …
• Плоские числа — числа, выраженные в виде произведения двух сомножителей (плоское число 6=2∙3): 4, 6, 8, 9, 10, 12, 14, 15, 16, 18, 20, 21, 22, 24, 25, 26, 27, 28, 30, 32, 33, 34, 35, 36, 38, 39, 40, 42, 44, 45, 46, 48, 49, 50, 51, 52, 54, 55, 56, 57, 58, 60, 62, …
Частным случаем являются прямоугольные числа, являющееся произведением двух последовательных целых чисел, то есть имеющие вид: n(n+1)
• Телесные числа — числа, выраженные произведением трёх сомножителей (телесное число 8=2∙2∙2): 8, 12, 16, 18, 20, 24, 27, 28, 30, 32, 36, 40, 42, 44, 45, 48, 50, 52, 54, 56, 60, 63, 64, 66, 68, 70, 72, 75, 76, 78, 80, 81, …
• Многоугольные числа (полигональные) — числа, ассоциированные с определённым многоугольником. Они в свою очередь делятся на: классические многоугольные числа, центрированные полигональные числа.
• Пространственные фигурные числа - числа, ассоциированные с определённым многогранником. Античные математики исследовали тетраэдральные и квадратные пирамидальные числа. Несложно определить числа, связанные с пирамидами, в основании которых лежит любой другой многоугольник.
2.1 Классические многоугольные числа
Есть основания полагать, что многоугольные числа возникли среди вавилонян при расчете мощения кирпичного пола. Из Вавилона они перешли к грекам. Диофант написал целую книгу о многоугольных числах (IV—III вв. до н. э.). Историки-математики утверждают, что треугольные числа были известны в Индии (во II в. до н. э.), в Китае (в 1309 г.). Многоугольными числами занимались многие математики: Ферма, Эйлер, Лагранж, Лежандр, Гаусс и др. Классические многоугольные числа являются разновидностью фигурных чисел. Они включают треугольные числа, квадратные числа, а также фигуры с любым количеством углов. Многоугольное число представляет собой количество равноудалённых точек в правильном геометрическом распределении определенного типа. Эти типы делятся на:
• Треугольные числа. Они имеют общую формулу: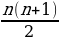 . Это такие числа, как: 1, 3, 6, 10, 15, 21, 28 … Их можно найти в виде точек в определенном правильном треугольнике.
. Это такие числа, как: 1, 3, 6, 10, 15, 21, 28 … Их можно найти в виде точек в определенном правильном треугольнике.
• Квадратные числа. Они имеют общую формулу: 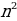 . Это такие числа, как: 1, 4, 9, 16, 25, 36, 49 … Они также представлены в виде точек в определенном квадрате.
. Это такие числа, как: 1, 4, 9, 16, 25, 36, 49 … Они также представлены в виде точек в определенном квадрате.
• Пятиугольные числа. Они имеют общую формулу: 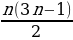 . Это числа, порядка: 1, 5, 12, 22, 35, 51, 70 …Они имеются в определенном пятиугольнике. И т.д.
. Это числа, порядка: 1, 5, 12, 22, 35, 51, 70 …Они имеются в определенном пятиугольнике. И т.д.
Таким образом, получают многоугольные числа различных порядков. Обозначается порядковое q-угольное число символом 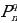 . Оно определяется по формуле:
. Оно определяется по формуле:
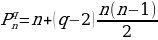
где 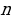 — порядковый номер n-угольного числа,
— порядковый номер n-угольного числа,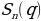 — сумма первых
— сумма первых 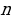 членов арифметической прогрессии, первый член которой равен нулю
членов арифметической прогрессии, первый член которой равен нулю 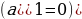 , а разность равна q - 2 .
, а разность равна q - 2 .
2.2 Центрированные полигональные числа
Центрированные полигональные числа — это класс фигурных чисел, каждое сформировано вокруг центральной точки, окружённой слоями многоугольников с постоянным числом сторон. Каждый слой содержит на k больше точек, чем предыдущий (где центр слоем не считается). Центрированные полигональные числа имеют виды (Приложение 1, рис.2):
• Центрированные треугольные числа 1, 4, 10, 19, 31, … (треугольник с точкой в центре и все остальные окружающие точки находятся на треугольных слоях). n - е по порядку центрированное треугольное число задаётся формулой:
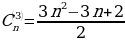
• Центрированные квадратные числа 1, 5, 13, 25, 41, … (квадрат с точкой в центре и все остальные окружающие точки, находящиеся на квадратных слоях). n - е по порядку центрированное 4-угольное (квадратное) число задаётся формулой:
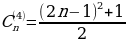
• Центрированные пятиугольные числа 1, 6, 16, 31, 51, … (пятиугольник, который содержит точку в центре и все точки, окружающие центр, лежат в пятиугольных слоях).
• Центрированные шестиугольные числа 1, 7, 19, 37, 61, … (шестиугольник с точкой в центре и все остальные окружающие точки находятся в шестиугольной решётке).
• Центрированные семиугольные числа 1, 8, 22, 43, 71, … (семиугольник с точкой в середине и все окружающие точки лежат на семиугольных слоях)
• Центрированные восьмиугольные числа 1, 9, 25, 49, 81, … (восьмиугольник с точкой в середине и все окружающие точки лежат на восьмиугольных слоях).
• Центрированные девятиугольные числа 1, 10, 28, 55, 91, … (девятиугольник с точкой в середине и все окружающие точки лежат на девятиугольных слоях).
• Центрированные десятиугольные числа 1, 11, 31, 61, 101, … (количество точек в десятиугольнике с точкой в середине и окружающими точками, лежащими на десятиугольных слоях), и так далее.
Как видно из приведенных диаграмм, n-ое центрированное k-угольного число может быть получена размещением k копий (n−1)-х треугольных чисел вокруг центральной точки; поэтому, n-ое центрированное k-угольного числа может быть выражено как: 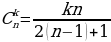
Так же, как и в случае обычных фигурных чисел, первое центрированное k-угольного число есть 1. Поэтому, для любого k, 1 является как k-угольным числом, так и центрированным k-угольным. Следующее число, являющееся как k-угольным, так и центрированным k-угольным, может быть найдено по формуле: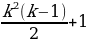 , которая показывает, что 10 является как треугольным, так и центрированным треугольным, а 25 является как четырехугольным, так и центрированным четырехугольным. Несмотря на то, что простое число p не может быть фигурным числом (кроме p-угольного), многие центрированные многоугольные числа являются простыми.
, которая показывает, что 10 является как треугольным, так и центрированным треугольным, а 25 является как четырехугольным, так и центрированным четырехугольным. Несмотря на то, что простое число p не может быть фигурным числом (кроме p-угольного), многие центрированные многоугольные числа являются простыми.
2.3 Пространственные фигурные числа
Наряду с рассмотренными выше фигурными числами для плоских фигур, можно определить пространственные или даже многомерные их аналоги.
Пирамидальные числа возникают при складывании круглых камушков горкой так, чтобы они не раскатывались. Получается пирамида. Каждый слой в такой пирамиде - треугольное число. Наверху один камушек, под ним - 3, под теми - 6 и т.д.: 1, 1+3=4, 1+3+6=10, 1+3+6+10=20, …
Пирамидальные числа определяются следующим образом -
n - е по порядку k-угольное пирамидальное число 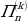 есть сумма первых n плоских фигурных чисел с тем же числом углов k:
есть сумма первых n плоских фигурных чисел с тем же числом углов k:
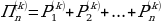
Треугольные пирамидальные (тетраэдральные) числа. Треугольные пирамидальные числа, называемые также тетраэдральными — это фигурные числа, которые представляют тетраэдр, то есть пирамиду, в основании которой лежит треугольник. Несколько первых тетраэдральных чисел:
1, 4, 10, 20, 35, 56, 84, 120, 165, 220, 286, 364, 455, 560, 680, 816, 969 … Интересно, что пятое число равно сумме всех предыдущих.
Общая формула для тетраэдрального числа: 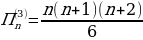 .
.
Фигурное представление чисел помогало пифагорейцам открывать законы арифметических операций, а также легко переходить к числовой характеристике геометрических объектов - измерению площадей и объемов. На сегодняшний день существует четкое понятие Многомерных фигурных чисел – это числа, которые могут быть выражены в виде равноудаленных точек в объемной многомерной фигуре. Их особенность в том, что они способны заполнять не только внешнюю фигурную оболочку, но и внутреннее пространство фигуры. Многомерные фигурные числа, как и многоугольные с полигональными, имеют тоже свои типы:
• Изоэдральные многомерные фигурные числа: Точнее сказать, все грани должны быть не просто равные, а должны быть транзитивны, то есть должны прилежать в одной и той же орбите симметрии. Изоэдральные многогранники называются изоэдрами. Они могут быть описаны их конфигурацией граней. Конфигурация граней - это сокращённое обозначение для представления вершинной фигуры многогранника или мозаики в виде последовательности граней вокруг вершины. Изоэдр может иметь как одинаковые грани, так и неодинаковые. (Приложение 1; рис.3)
• Элементарные многомерные фигурные числа:
1) Гиперкубические: Куб, который находится в неопределенном x-мерном пространстве, т.е. это пространство может иметь много граней, относящихся к этому кубу. (Приложение 2; рис. 4)
2) Симплексные: Симплекс или n-угольный тетрайдер — геометрическая фигура, являющаяся n-мерным обобщением треугольника. Простейший n-мерный многогранник с количеством вершин n + 1 как раз и называется симплексом (принято также название «n-мерный тетраэдр»). В пространствах низшей размерности этому определению соответствуют такие фигуры:
• 0-симплекс (точка) — 1 вершина;
• 1-симплекс (отрезок) — 2 вершины;
• 2-симплекс (треугольник) — 3 вершины;
• 3-симплекс (тетраэдр) — 4 вершины.
3) Гипероктаэдрные: Гиперокта́эдр — геометрическая фигура в n-мерном пространстве, которое имеет размерность, равную 3: правильный политоп, двойственный n-мерному гиперкубу. Другие названия: кокуб, ортоплекс, кросс-политоп. Гипероктаэдр может быть как в упрощенной, так и в усложненной форме, где в одной фигуре может находиться несколько таких же. (Приложение 2; рис.5)
• Трехмерные правильные фигурные числа: Трехмерный многогранник (Сокращение 3D обозначает трёхмерное пространство) – совокупность конечного числа плоских многоугольников в трехмерном пространстве, такая, что: каждая сторона любого из многоугольников есть одновременно сторона другого, смежного с ним и такая система является круговой, или по другому замкнутой.
• Четырехмерные правильные фигурные числа: Четырёхмерное пространство (обозначения: 4D) — математический объект, обобщающий свойства трёхмерного пространства. Алгебраически четырёхмерное пространство может быть построено как множество векторов с четырьмя вещественными координатами. Геометрически в простейшем случае четырёхмерное пространство рассматривается как пространство размерности четырёх измерений.
2.4 Роль в теории чисел
Треугольник Паскаля. Числа из треугольника Паскаля обнаруживают связь со многими типами фигурных чисел. На третьей линии в треугольнике Паскаля находятся треугольные числа, а на четвёртой — тетраэдральные числа (Приложение 2, рис.6). Это объясняется тем, что n-е тетраэдральное число есть сумма первых n треугольных чисел, которые расположены на третьей линии. Аналогично на пятой линии расположены четырёхмерные пентатопные числа и т. д. Все они, как и прочие числа внутри треугольника Паскаля, являются биномиальными коэффициентами.
Таким образом, все внутренние элементы треугольника Паскаля являются фигурными числами, причём представлены различные их типы. Вдоль каждой строки, слева направо, идут гипертетраэдральные числа возрастающей размерности. Известно, что сумма всех чисел n-й строки равна 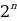 отсюда следует, что сумма всех чисел первых n строк равна числу Мерсенна
отсюда следует, что сумма всех чисел первых n строк равна числу Мерсенна 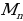 .Следовательно, число Мерсенна можно представить как сумму гипертетраэдральных чисел.
.Следовательно, число Мерсенна можно представить как сумму гипертетраэдральных чисел.
III. Значение фигурных чисел в нашей жизни
Значение фигурных чисел в нашей жизни во все времена было очень важным: с момента, когда первобытные люди только начали учиться считать, и до того, как современное общество живет сейчас. Новые технологии постоянно появлялись в различных сферах деятельности:
• Упаковка товара на фабрике в линейном порядке.
• На выступлениях синхронистки располагаются правильными рядами, образуя фигуры (плоские числа).
• Самолёты в воздухе образуют треугольные или другие фигурные числа, во время парада.
Важное использование фигурных чисел преобладает в строительстве архитектуры. Например, чтобы построить театральное здание, научный архитектор должен знать, как правильно установить конкретную колонну под определенным углом, чтобы она не упала и не сдвинулась,аи в то же время работа была выполнена точно согласно приведенному чертежу будущего здания. Для этого архитектор должен провести определенную серию математических расчетов и измерений, присущих колонне и месту, где она будет стоять. Колонна – это фигура, которая имеет свои физические фигурные особенности. В живописи и дизайне фигурные числа играют роль особенностей создания требуемого изображения. Например, используя идею фигуры, вы можете создать трехмерную картинку, в которой объем и тень изображения будут четко видны. Так же разные многомерные фигуры используются в кинематографе и компьютерной графике для создания объемного изображения. Это 3D, 4D, 5D фильмы. Без многомерных фигур мы бы не знали, как посмотреть на экранную картинку в пространстве с разных точек.
Заключение
В процессе работы по данной проблеме я достигла цели, поставленной в начале исследования: изучила фигурные числа.
Без такого богатого разнообразия использования фигурных чисел нашу жизнь трудно представить. Эти числа способствовали, развитию архитектуры, живописи и искусства. Фигурные числа являются основным компонентом молекулярной системы, так как молекулы по своей природе имеют определенное количество и структуру в любом материальном теле. И для того, чтобы изучить это не только визуально, но и с помощью рассуждений, в мире появились фигурные числа. Они имеют широкий спектр видов, подвидов и используются в различных сферах человеческой деятельности.
Список использованной литературы
https://ru.wikipedia.org/wiki/Фигурные_числа
Деза Е., Деза М., 2016.
О.Оре. Приглашение в теорию чисел. М.: Наука.1980.
Ожигова Е. П. Что такое теория чисел. — М.: Знание, 1970.
Шалаева Г.П. «Новейший справочник школьника 4-11 классы»
Юшкевич А.П. « История математики с древнейших времен до начала XIX столетия. Том 2»
Приложения
Приложение 1

Рис. 1 Представление чисел древних людей
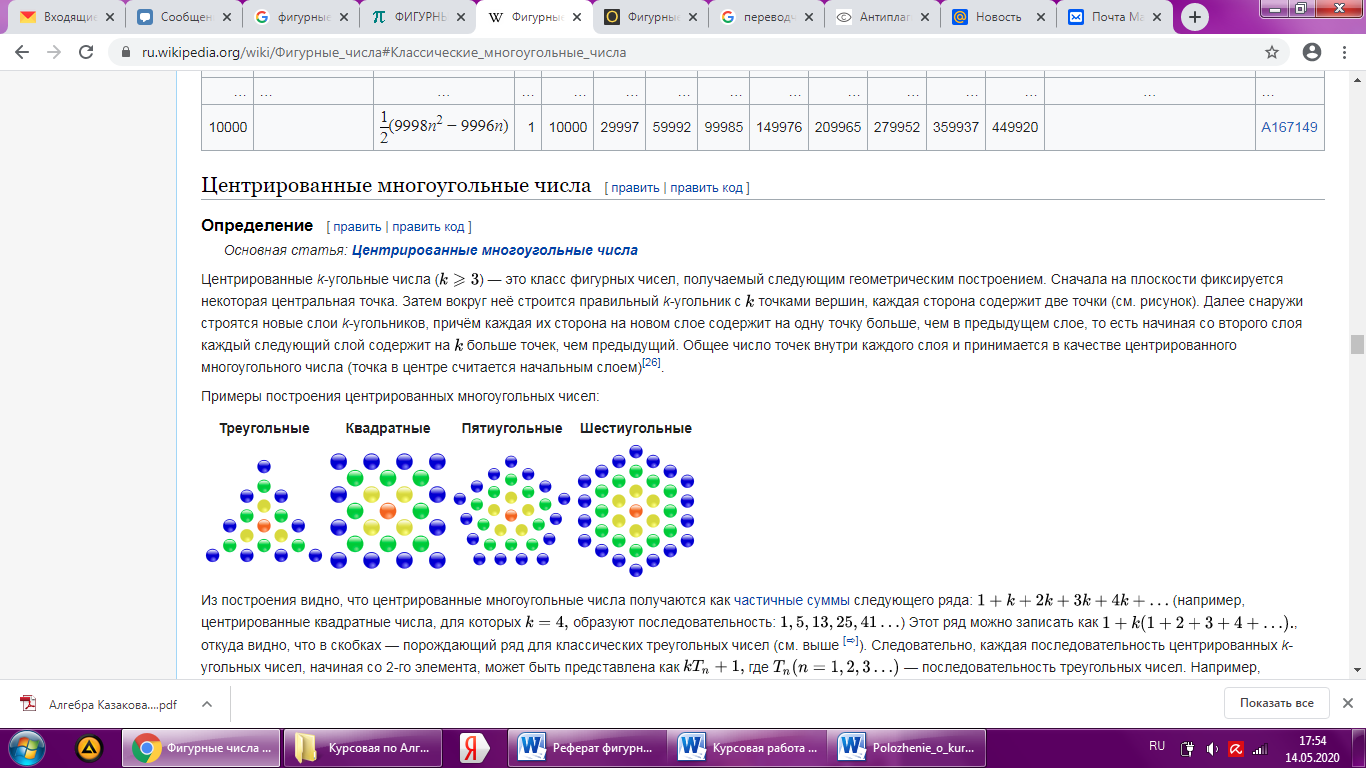
Рис.2 Примеры построения центрированных многоугольных чисел
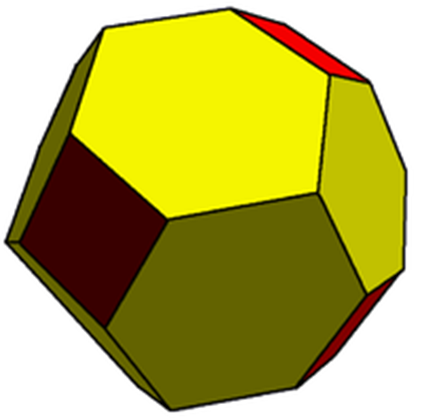
Рис. 3 Изоэдральная многомерная фигура
Приложение 2

Рис. 4 Гиперкубическая многомерная фигура
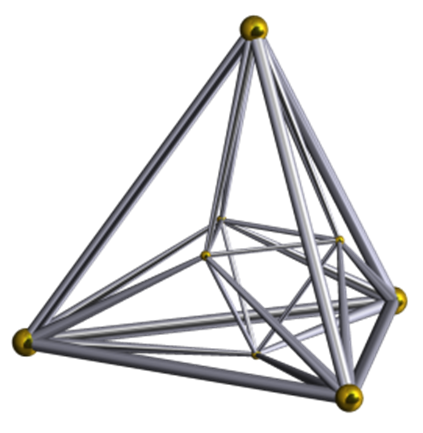
Рис. 5 Гипероктаэдрная фигура

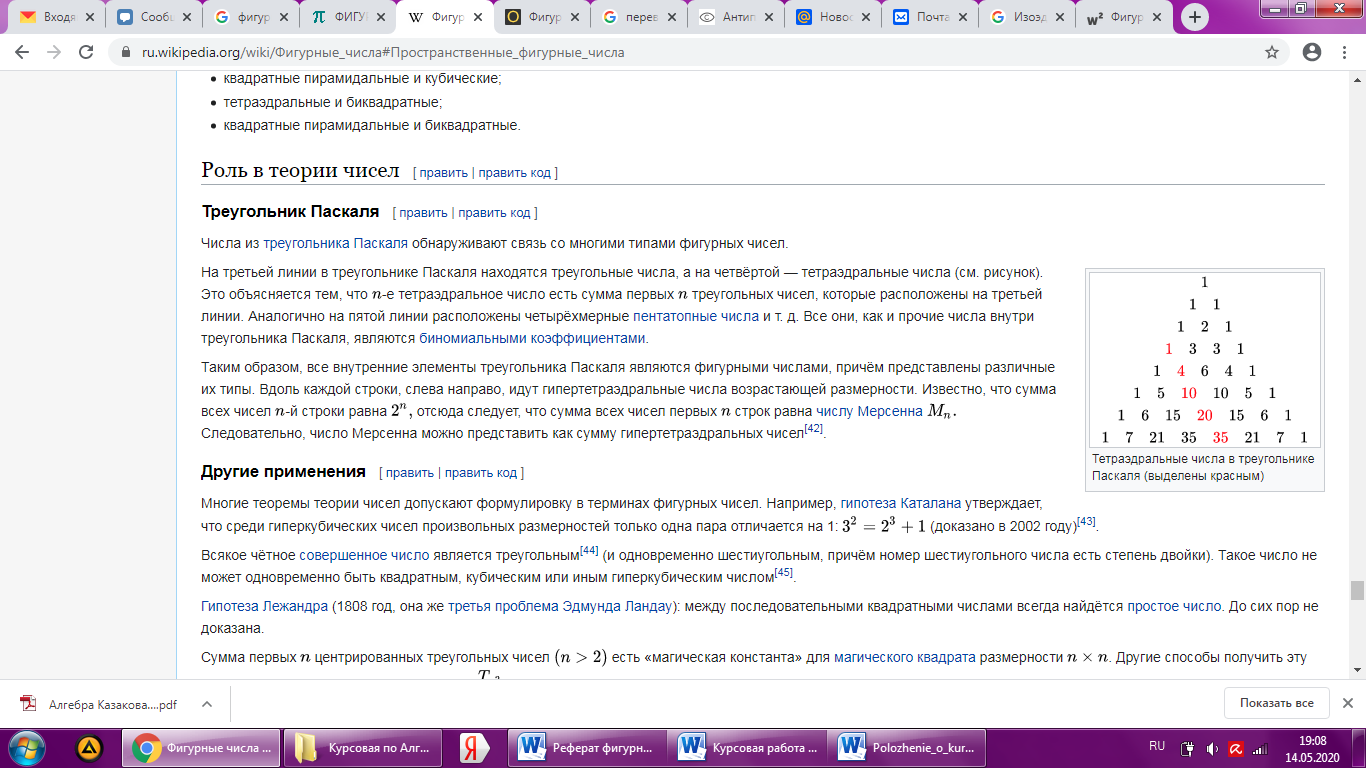
Рис.6 Треугольник Паскаля






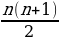 . Это такие числа, как: 1, 3, 6, 10, 15, 21, 28 … Их можно найти в виде точек в определенном правильном треугольнике.
. Это такие числа, как: 1, 3, 6, 10, 15, 21, 28 … Их можно найти в виде точек в определенном правильном треугольнике.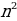 . Это такие числа, как: 1, 4, 9, 16, 25, 36, 49 … Они также представлены в виде точек в определенном квадрате.
. Это такие числа, как: 1, 4, 9, 16, 25, 36, 49 … Они также представлены в виде точек в определенном квадрате.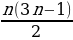 . Это числа, порядка: 1, 5, 12, 22, 35, 51, 70 …Они имеются в определенном пятиугольнике. И т.д.
. Это числа, порядка: 1, 5, 12, 22, 35, 51, 70 …Они имеются в определенном пятиугольнике. И т.д.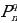 . Оно определяется по формуле:
. Оно определяется по формуле: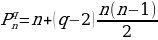
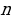 — порядковый номер n-угольного числа,
— порядковый номер n-угольного числа,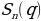 — сумма первых
— сумма первых 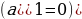 , а разность равна q - 2 .
, а разность равна q - 2 .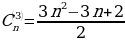
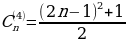
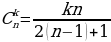
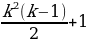 , которая показывает, что 10 является как треугольным, так и центрированным треугольным, а 25 является как четырехугольным, так и центрированным четырехугольным. Несмотря на то, что простое число p не может быть фигурным числом (кроме p-угольного), многие центрированные многоугольные числа являются простыми.
, которая показывает, что 10 является как треугольным, так и центрированным треугольным, а 25 является как четырехугольным, так и центрированным четырехугольным. Несмотря на то, что простое число p не может быть фигурным числом (кроме p-угольного), многие центрированные многоугольные числа являются простыми.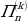 есть сумма первых n плоских фигурных чисел с тем же числом углов k:
есть сумма первых n плоских фигурных чисел с тем же числом углов k: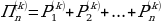
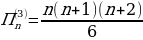 .
.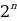 отсюда следует, что сумма всех чисел первых n строк равна числу Мерсенна
отсюда следует, что сумма всех чисел первых n строк равна числу Мерсенна 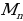 .Следовательно, число Мерсенна можно представить как сумму гипертетраэдральных чисел.
.Следовательно, число Мерсенна можно представить как сумму гипертетраэдральных чисел.
















