|
|
|
| 1.Пересечение множеств и событий
2. Объединение множеств и событий
3. Разность множеств и событий
4.Симметрическая разность множеств и событий
5. Переход к противоположному событию
| Пересечением двух множеств называется множество, которому принадлежат те и только те элементы, которые одновременно принадлежат двум данным множествам. 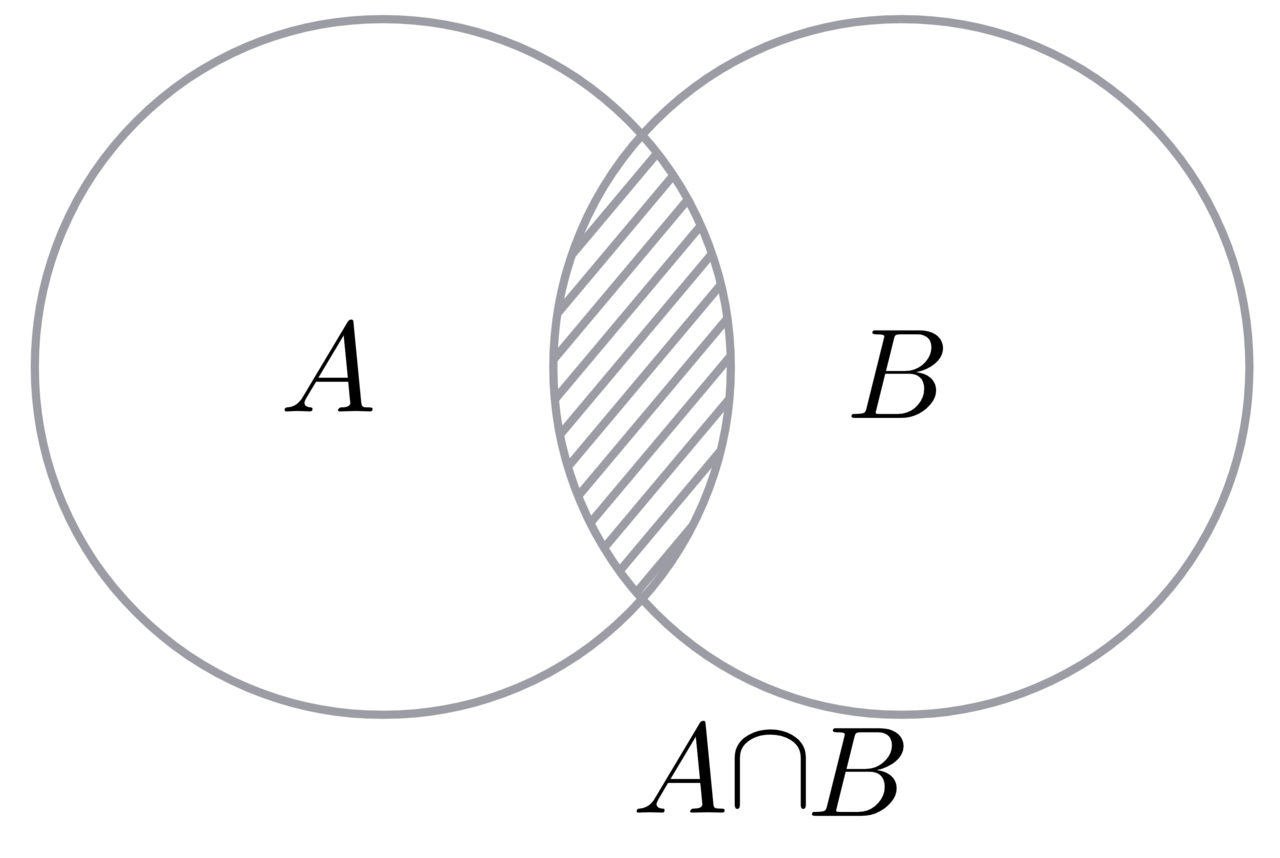 Пример: Для множеств 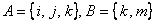 : :
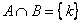 Если у множеств нет одинаковых элементов, то их пересечение пусто:
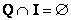 , так как множества , так как множества 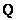 и и  не пересекаются – то есть ни одно иррациональное число невозможно представить в виде не пересекаются – то есть ни одно иррациональное число невозможно представить в виде 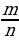 рациональной дроби. рациональной дроби.
Объединением двух множеств называется множество, состоящее из тех и только тех элементов, которые принадлежат хотя бы одному из данных множеств. 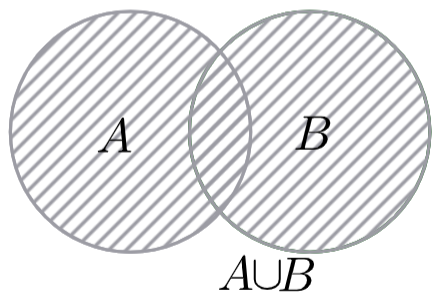
Пример: Дано: 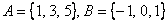 Запишем объединение множеств:
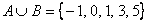 , т.е. необходимо перечислить все элементы множеств А и В , причём одинаковые элементы (в данном случае единица на пересечении множеств) следует указать один раз. , т.е. необходимо перечислить все элементы множеств А и В , причём одинаковые элементы (в данном случае единица на пересечении множеств) следует указать один раз. Но множества, разумеется, могут и не пересекаться, как это имеет место быть с рациональными и иррациональными числами:
 В этом случае можно изобразить два непересекающихся заштрихованных круга. 3) Операция объединения применима и для бОльшего количества множеств, например, если  , то: , то: 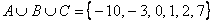 (при этом числа вовсе не обязательно располагать в порядке возрастания), или (при этом числа вовсе не обязательно располагать в порядке возрастания), или 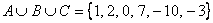
Разностью двух множеств называется множество, состоящее из тех и только тех элементов, которые входят в первое множество, но не входят во второе. 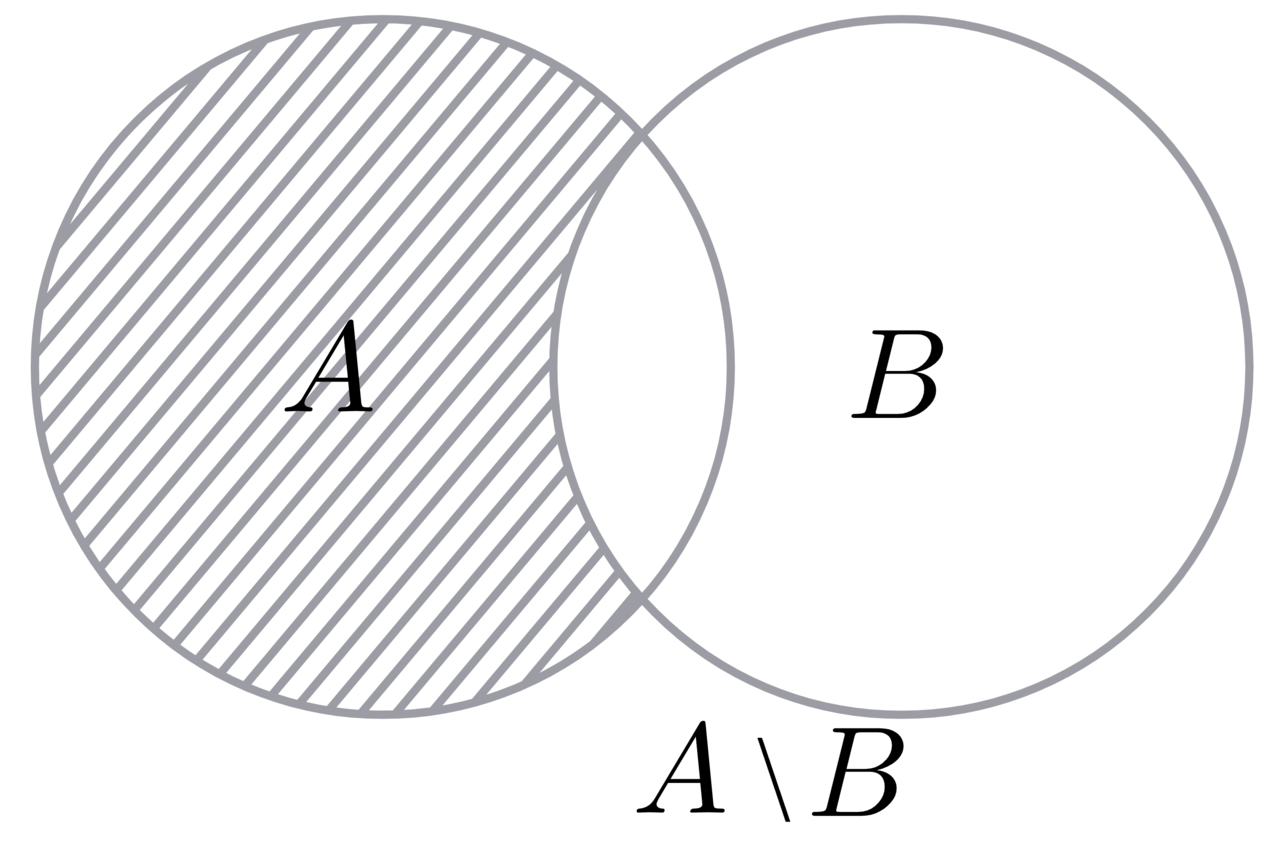
Пример: Рассмотрим множества 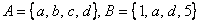 . Чтобы записать разность А\В, нужно из множества А «выбросить» все элементы, которые есть во множестве В: . Чтобы записать разность А\В, нужно из множества А «выбросить» все элементы, которые есть во множестве В:
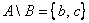 Пример с числовыми множествами:
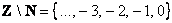 – здесь из множества целых чисел исключены все натуральные, да и сама запись – здесь из множества целых чисел исключены все натуральные, да и сама запись 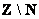 так и читается: «множество целых чисел без множества натуральных». так и читается: «множество целых чисел без множества натуральных».
Симметрической разностью двух множеств и называется множество, которое состоит из элементов, принадлежащих ровно одному из данных множеств. 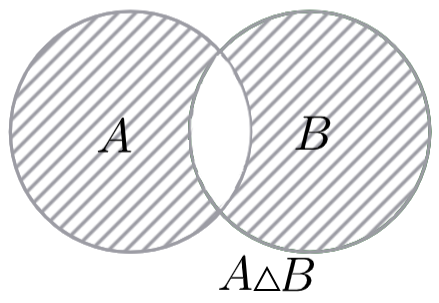
| Пересечением (произведением) двух событий A и B называют такое событие, которое состоит из всех элементов, входящих как в событие A , так и в событие B (рис. 1). 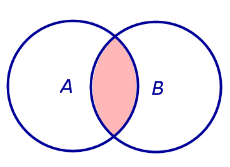
Событие 
Операцию пересечения (произведения) двух событий A и B обозначают 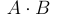 , или AB, или , или AB, или 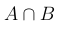 . .
Независимые события - Два события независимы, если при наступлении одного вероятность наступления другого не изменяется. Правило умножения вероятностей независимых событий Вероятность определенной последовательности независимых событий равна произведению вероятностей каждого из событий
Пример: Вероятность того, что аккумулятор заряжен, равна 0,85. Покупатель в магазине приобретает случайную упаковку, которая содержит два таких аккумулятора. Найдите вероятность того, что оба аккумулятора в этой упаковке окажутся заряжены. Решение: Найдём вероятность события «оба аккумулятора заряжены». Обозначим через A и B события «первый аккумулятор заряжён» и «второй аккумулятор заряжён». Получили P(A)=P(B)=0,85.P(A) = P(B) = 0,85.P(A)=P(B)=0,85. Событие «оба аккумулятора заряжены» — это пересечение событий A∩B, его вероятность равна P(A∩B)= P(A)⋅P(B)= 0,85⋅0,85= 0,7225. Ответ: 0,7225
Объединением (суммой) двух событий A и B называют такое событие, которое состоит из элементов события A и элементов события B 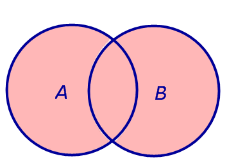
Событие A + B
Операцию объединения (суммы) двух событий A и B обозначают A + B или  Несовместимые события – события, которые в одном и том же испытании не могут произойти одновременно Вероятности несовместных событий складываются. Теорема 1. Вероятность суммы двух несовместных событий А и В (появления хотя бы одного события) равна сумме вероятностей этих событий: P (А+В)= P (A)+ P (B) Теорема обобщается на любое число попарно несовместных событий.
Пример: 1)Бросают игральную кость 1 раз. Найдите вероятность того, что выпало число, большее 3. Решение. При бросании игральной кости могут выпадать числа 1,2,3,4,5 и 6 с равной вероятностью 1/6. Нас интересует выпадение одного из чисел 4, 5 или 6 при первом бросании игральной кости и выпадение таких же чисел при втором бросании. Вероятность появления одного из чисел 4, 5 или 6 равна сумме вероятности этих событий, т.е. Р=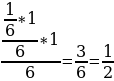 Ответ: 0,5 2) На экзамене по биологии школьнику достаётся один случайно выбранный вопрос из списка. Вероятность того, что этот вопрос на тему «Членистоногие», равна 0,15. Вероятность того, что это окажется вопрос на тему «Ботаника», равна 0,45. В списке нет вопросов, которые одновременно относятся к этим двум темам. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем. Решение:Р (А) = 0,15 + 0,45 = 0,6 Ответ: 0,6 .
Р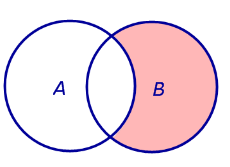 азностью событий A и B называют событие, состоящее из тех элементов события A , которые не входят в событие B азностью событий A и B называют событие, состоящее из тех элементов события A , которые не входят в событие B
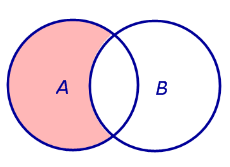
Событие A \ B Событие B \ A
Операцию разности двух событий A и B обозначают A \ B
Симметрической разностью событий A и B называют событие, состоящее из тех элементов события A , которые не входят в событие B , а также из тех элементов события B , которые не входят в событие A С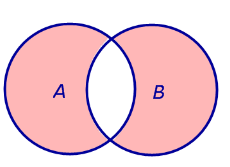 обытие А обытие А В В
Операцию симметрической разности двух событий A и B обозначают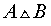
Переход к противоположному событию 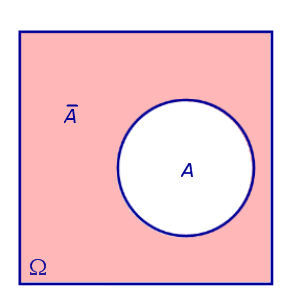
| Событие  |
Противоположным событием к событию A называют событие, состоящее из тех элементов всего множества элементарных событий Ω , которые не входят в событие A Событие, противоположное к событию A , обозначают 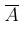 . . Следствие из теоремы 1. Сумма вероятностей противоположных событий А и 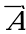 равна 1: равна 1: P (A)+ P (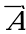 )= 1. )= 1.
Пример: 1)Вероятности попадания в цель при стрельбе из трех орудий таковы: p1=0,8; p2=0,7; p3=0,9. Найти вероятность хотя бы одного попадания (событие А) при одном залпе из всех орудий. Решение. Вероятность попадания в цель каждым из орудий не зависит от результатов стрельбы из других орудий, поэтому рассматриваемые события  (попадание первого орудия), (попадание первого орудия), 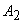 (попадание второго орудия) и (попадание второго орудия) и 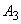 (попадание третьего орудия) независимы в совокупности. (попадание третьего орудия) независимы в совокупности.
Вероятности событий, противоположных событиям 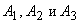 (т.е. вероятности промахов), соответственно равны: (т.е. вероятности промахов), соответственно равны: 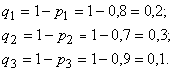 Искомая вероятность 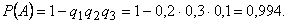 |
Практикум по теме ЗАДАЧИ ДЛЯ СОВМЕСТНОГО РЕШЕНИЯ Задача 1. В корзине 7 черных и 9 белых шаров. Из корзины вынимают последовательно два шара, после вынимания первого он возвращается в корзину. Найдите вероятность того, что: 1.Оба шара будут белыми; 2. Оба шара будут черными; 3. Вынуты разноцветные шары. Решение: 1. Событие А – вынули два белых шара. Р(А)=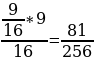 2. Событие В - оба шара будут черными. Р(А)=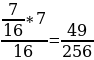 3. Событие С - вынуты разноцветные шары. Р(А)=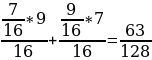 Задача 2. Два стрелка независимо друг от друга стреляют по мишени. Вероятность попадания первого стрелка равна 0,5, второго - 0,7. Найдите вероятности: Хотя бы одного попадания; Ровно одного попадания; Ровно двух попаданий; Не больше одного попадания; Попадания в мишень не раньше, чем при втором выстреле, если каждый сделал по одному выстрелу. Решение: Событие А – попал первый стрелок, В – попал второй стрелок. Р(А)=0,5, P (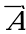 )=1-0,5=0,5, )=1-0,5=0,5, Р(В)=0,7, P (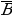 )=1-0,7=0,3 )=1-0,7=0,3 Событие С - хотя бы одно попадание. Р(С)=0,5*0,7+0,5*0,3+0,5*0,7=0,85; Событие D - ровно одного попадание. Р(D)=0,5*0,7+0,5*0,3=0,5; Событие Е - ровно два попадания. Р(Е)=0,5*0,7=0,35; Событие F - не больше одного попадания. P(F)=0,5*0,3+0,5*0,3+0,7*0,5=0,65; Событие Х - попадания в мишень не раньше, чем при втором выстреле, если каждый сделал по одному выстрелу. Р(Х) = 0,5*0,7+0,5*0,3=0,5. Задача 3. Три стрелка независимо друг от друга стреляют по мишени. Вероятность попадания первого стрелка равна 0,3, второго - 0,4, третьего - 0,5. Найдите вероятности: Ни одного попадания; Хотя бы одного попадания; Ровно одного попадания; Хотя бы двух попаданий; Ровно двух попаданий; Трех попаданий; Не больше одного попадания; Не больше двух попаданий, если каждый сделал по одному выстрелу. Решение: Событие А – попал первый стрелок, событие В – попал второй стрелок, событие С - попал третий стрелок. Р(А)=0,3, P (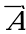 )=1-0,3=0,7, )=1-0,3=0,7, Р(В)=0,4, P (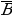 )=1-0,4=0,6; )=1-0,4=0,6; Р(С)=0,5, P (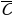 )=1-0,5=0,5; )=1-0,5=0,5; Событие D - ни одного попадания; P(D)=0,7*0,6*0,5=0,21 Событие Е - хотя бы одно попадание; Р(Е)=0,7*0,6*0,5+0,7*0,4*0,5+0,3*0,6*0,5+0,7*0,4*0,5+0,3*0,4*0,5+0,3*0,6*0,5+0,3*0,4*0,5=0,79 Событие F - ровно одно попадание; P(F)= 0,7*0,6*0,5+0,7*0,4*0,5+0,3*0,6*0,5=0,44 Событие К - хотя бы два попадания; Р(К)=0,3*0,4*0,5+0,3*0,6*0,5+0,7*0,4*0,5+0,3*0,4*0,5=0,35 Событие L - ровно два попадания; P(L)=0,7*0,4*0,5+0,3*0,4*0,5+0,3*0,6*0,5=0,29 Событие М - три попадания; Р(М) = 0,3*0,4*0,5=0,06 Событие N - не больше одного попадания; P(N)=0,7*0,6*0,5+0,3*0,6*0,5+0,7*0,4*0,5+0,7*0,6*0,5=0,65 Событие О - не больше двух попаданий, если каждый сделал по одному выстрелу. Р(О) = 0,7*0,6*0,5+0,7*0,4*0,5+0,3*0,6*0,5+0,7*0,6*0,5+0,3*0,4*0,5+0,7*0,4*0,5+0,3*0,6*0,5=0,94.
ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ: Задача 1. В корзине 6 черных и 10 белых шаров. Из корзины вынимают сразу два шара. Найдите вероятность того, что: Оба шара будут белыми; Ответ: 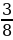 ; ; 2. Оба шара будут черными; Ответ: 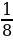 ; ; 3. Вынуты разноцветные шары. Ответ: 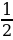 ; ; Задача 2. Два стрелка независимо друг от друга стреляют по мишени. Вероятность попадания первого стрелка равна 0,3, второго - 0,9. Найдите вероятности: Хотя бы одного попадания; Ответ: 0,93; Ровно одного попадания; Ответ: 0,66; Ровно двух попаданий; Ответ: 0,27; Не больше одного попадания; Ответ: 0,73; Попадания в мишень не раньше, чем при втором выстреле, если каждый сделал по одному выстрелу. Ответ: 0,66. Задача 3. Три стрелка независимо друг от друга стреляют по мишени. Вероятность попадания первого стрелка равна 0,2, второго - 0,4, третьего - 0,6. Найдите вероятности: Ни одного попадания; Ответ: 0,192; Хотя бы одного попадания; Ответ: 0,808; Ровно одного попадания; Ответ: 0,464; Хотя бы двух попаданий; Ответ:0,28; Ровно двух попаданий; Ответ:0,296; Трех попаданий; Ответ:0,048; Не больше одного попадания; Ответ:0,656; Не больше двух попаданий, если каждый сделал по одному выстрелу. Ответ: 0,952.
ТЕСТ «Сложение и умножение вероятностей. »
1. Как называется событие, которое состоит в том, что происходит хотя бы одно из данных событий А и B? Сумма событий A и B Произведение событий A и B Отношение событий A и B 2. Могут ли события быть одновременно и несовместными и совместными? А) да Б) нет В) не знаю 3. Входит ли в понятие суммы событий (А + В) событие, состоящее в одновременном наступлении события А и события В? А) да Б) нет В) не знаю 4. Из полной колоды карт вынимается одна карта. Выяснить, являются совместными или несовместными события: «вынута карта красной масти» и «вынут валет»; А) да Б) нет В) не знаю 5. Вероятность попадания мяча в корзину, брошенного один раз некоторым баскетболистом, равна 0,6. Чему равна вероятность того, что, бросив мяч в корзину, этот баскетболист промахнётся? А) 0,36 Б) 1 В) 0,4 6. Из колоды карт (36 шт.) вынута одна карта. Найти вероятность того, что это "дама" или "король". А) 2/9 Б) 4/9 В) 8/9 7 Из колоды в 36 карт наудачу вынимается одна. Какова вероятность того, что будет вынута карта бубновой масти или туз? А) ½ Б) 1/18 В) 1/3 Ответы: | 1 | 2 | 3 | 4 | 5 | 6 | 7 | | А | Б | Б | А | В | А | В | 6 – 7 «+» - отметка 5 4 – 5 «+» - отметка 4 2 - 3 «+» - отметка 3 1 «+» - отметка 2
|







 рациональной дроби.
рациональной дроби.




 азностью событий A и B называют событие, состоящее из тех элементов события A , которые не входят в событие B
азностью событий A и B называют событие, состоящее из тех элементов события A , которые не входят в событие B
 обытие А
обытие А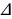 В
В
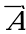 равна 1:
равна 1: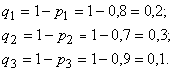
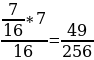
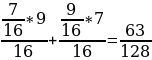
 )=1-0,7=0,3
)=1-0,7=0,3 )=1-0,5=0,5;
)=1-0,5=0,5;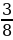 ;
;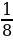 ;
;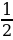 ;
;









