Оценочные средства для текущего контроля знаний по геометрии по ФГОС (2021) на 2024-25 уч.г.

Оценочные материалы по учебному предмету «Геометрия» для обучающихся 7-9 классов

Контрольно-оценочные средства по геометрии в 7-9 классе (Л.С.Атанасян, В.Ф.Бутузов, С.Б. Кадомцев, Э.Г. Позняк, И.И.Юдина)

СПЕЦИФИКАЦИЯ

контрольно-измерительных материалов для проведения контрольных работ по геометрии в 7 классе

1. Назначение работы – проверка знаний, умений, навыков, полученных учащимися при изучении этой главы.

2. Характеристика структуры и содержания работы Работа по геометрии состоит из 3-х частей:

Уровень А включает 2 задания, которые позволяют выявить знания и умения на базовом уровне.

Уровень В включает 1 задание, которое позволяет выявить знания и умения на базовом уровне с полным решением геометрической задачи.

Уровень С включает 1 задание, позволяют выявить умения и навыки выполнения заданий на применение знаний и умений, способов деятельности в изменённой ситуации и в незнакомой ситуации.

Таблица 1. Распределение заданий по частям работы

№	Части работы	Число заданий	Максимальный балл	Тип заданий
1	Уровень А	2	2	Задания с выбором ответа базового уровня
2	Уровень В	1	3	Задания с полным решением базового уровня сложности

4. Время выполнения работы – 40 минут (без учёта времени, отведённого на инструктаж учащихся).

5. Система оценивания отдельных заданий и работы в целом

Для оценивания результатов выполненных работ учащийся используется общий балл. В таблице 2 приводятся критерии оценивания входной контрольной работы.

Максимальный балл работы в целом – 9.

Критерии оценивания контрольной работы

Таблица 2

Шкала перевода общего балла в школьную отметку Таблица 3

Контрольная работа № 1 по теме «Треугольники»

Распределение заданий по элементам содержания и требований к уровню подготовки обучающихся для проведения входной контрольной работы.

Таблица

Номер задания		Предметные умения и универсальные учебные действия
		предметные	познавательные	регулятивные
А1, А2,		Строить и обозначать треугольник; медиану, биссектрису, высоту треугольника; окружность. Выполнять построение треугольника с помощью циркуля и линейки. Находить периметр треугольника.	Определять способы действий в рамках предложенных условий и требований	Принимать и сохранять учебную задачу. Выполнять учебные действия
В, С		Решать задачи на применение признаков равенства треугольников и на построение треугольника по трём элементам с полным рассуждением и доказательством.	Осуществлять логические операции (аналогия, анализ, синтез)	Самостоятельно планировать пути достижения целей познавательной деятельности

Контрольная работа №2 по теме "Параллельные прямые, сумма углов треугольника"

Распределение заданий по элементам содержания и требований к уровню подготовки обучающихся для проведения входной контрольной работы.

Таблица 4

Номер задания	Предметные умения и универсальные учебные действия
	предметные	познавательные	регулятивные
А1, А2,	Строить и обозначать параллельные прямые Различать соответственные, накрест лежащие и односторонние углы. Строить эти углы.	Определять способы действий в рамках предложенных условий и требований	Принимать и сохранять учебную задачу. Выполнять учебные действия
	Понимать смысл аксиом и обратной теоремы
В,С	Решать задачи на применение признаков параллельности двух прямых. Использовать при решении теоремы об углах, образованных параллельными прямыми	Осуществлять логические операции (аналогия, анализ синтез)	Самостоятельно планировать пути достижения целей познавательной деятельности

Контрольная работа № 3 по теме

Окружность и круг. Геометрические построения

Цель: проверить уровень усвоения по теме «Треугольники»:

• окружность и ее элементы;

• свойства равнобедренного треугольника;

• взаимное расположение прямой и окружности;

• свойство касательной к окружности;

• признаки равенства прямоугольных треугольников;

• понимание серединного перпендикуляра отрезка как ГМТ;

• понимание биссектрисы угла как ГМТ;

• умение выполнять чертежи и оформлять решение задачи.

Структура контрольной работы:

Тематическая контрольная работа состоит из 5 заданий базового уровня. На выполнение работы отводится 40 минут. Спецификация заданий и критерии оценивания

№ задания	Характеристика задания	Проверяемые элементы содержания	Балл за выполнение проверяемого элемента	Балл за выполнени е задания
1	Нахождение заданного угла в окружности	Знание свойств равнобедренного треугольника	1 балл	2 балла
		Знание теоремы о внешнем угле треугольника	1 балл
2	Нахождение длины заданного отрезка в окружности	Знание свойства касательной	1 балл	2 балла
		Знание свойств прямоугольного треугольника	1 балл
3	Доказательство равенства углов (отрезков)	Знание свойств равнобедренного треугольника	1 балл	3 балла
		Умение доказывать равенство прямоугольных треугольников	1 балл
		Умение делать вывод	1 балл
4	Построение треугольника	Умение построением находить середину отрезка	1 балл	4 балла
		Умение строить треугольник по трем сторонам	1 балл
		Умение описывать построение	2 балла
5	Решение задачи на применение геометрического места точек	Умение строить серединный перпендикуляр	1 балл	3 балла
		Умение доказывать правильность нахождений полученных точек	2 балл

Шкала перевода первичного балла за выполнение работы в отметку по пятибалльной шкале:

Первичный балл	0 - 6	7 – 9	10 – 12	13 – 14
Отметка	2	3	4	5

Содержание контрольной работы

Вариант 1

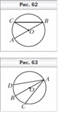
1. На рисунке 62 точка O — центр окружности, ABC = 28°.

Найдите угол AOC.

1. К окружности с центром O проведена касательная CD (D — точка касания) Найдите отрезок OC, если радиус окружности равен 6 см и DCO= 30°.

2. В окружности с центром O проведены диаметр AB и хорды AC и AD так, что BAC = BAD (рис. 63). Докажите, что AC = AD.

3. Постройте равнобедренный треугольник по боковой стороне и медиане, проведённой к ней.

4. Даны окружность и две точки вне её. Найдите на окружности точку, равноудалённую от этих двух точек. Сколько решений может иметь задача?

Контрольная работа №4 итоговая за курс геометрии 7 кл

Пояснительная записка:

Контрольная работа за год по геометрии для 7 общеобразовательного класса .

Время выполнения работы – 1 час.

Система оценивания работы: 1 часть (задача №1-6) – 1 балл

2 часть -задача № 7 – 2 балла, задача №8 – 3 балла.

Максимальное число баллов – 11 баллов

Оценивание работы: оценка «5» - 10-11 баллов

оценка «4» - 7-9 баллов

оценка «3» - 5-6 баллов

оценка «2» - менее 5 баллов.

Спецификация работы:

	Часть 1	Часть2
Число заданий	6	2
Тип заданий и форма ответа	С выбором варианта ответа	С подробным решением
Уровень сложности	базовый	повышенный
Проверяемый учебный материал	геометрия 7 класса	геометрия 7 класса

I вариант

1 часть - тест

1). Один из смежных углов равен 40⁰ . Чему равен другой угол?

А.40⁰ Б. 140⁰ В.180⁰ Г. невозможно вычислить

2). Выберите правильное утверждение:

А. Две прямые параллельны, если накрест лежащие углы равны.

Б. Две прямые параллельны, если вертикальные углы равны.

В. Две прямые параллельны, если односторонние углы равны.

Г. Две прямые параллельны, если сумма соответственных углов равна 180⁰.

3). Два угла треугольника равны 107⁰ и 23⁰. Чему равен третий угол этого треугольника?

А.130⁰ Б. 107⁰ В. 50⁰ Г. невозможно вычислить

4). Выберите правильное утверждение:

А. Два треугольника равны, если в двух треугольниках равны по две стороны

и по одному углу.

Б. Два треугольника никогда не равны.

В. Два треугольника равны, если в одном треугольнике равны две стороны

и углы.

Г. Два треугольника равны, если в двух треугольниках равны по две стороны

и по углу между ними.

5). В равнобедренном треугольнике угол при основании равен 70⁰ .Чему равны

остальные углы?

А.70⁰ и 70⁰ Б. 55⁰ и 55⁰ В. 70⁰ и 40⁰ Г. невозможно вычислить

6). Треугольник АВС- равнобедренный (АВ=ВС). ВD-высота.

ВD=4 м, АС= 6 м, АВ=5 м. Чему равны стороны треугольника ВDС.

В

А С

D

А. 5м, 4м и 4м Б. 3м, 5м и 4м. В. 5м, 4м и 5м Г. невозможно вычислить.

2 часть – решите задачи.

7 ). d в По чертежу найдите угол 1, если

123⁰ известно, что в  с.

с Запишите дано, найти, решение.

1

8). Параллельные прямые а и в пересечены двумя параллельными секущими АВ и СD, причем А и С принадлежат прямой а, В и D – прямой в .

Докажите, что АС=ВD.

II вариант

1 часть – тест

1). Два угла треугольника равны 116⁰ и 34⁰. Чему равен третий угол этого треугольника?

А. невозможно вычислить Б. 116⁰ В.150⁰ Г. 30⁰

2). Выберите правильное утверждение:

А. Два треугольника равны, если в двух треугольниках равны по стороне

и по двум прилежащим к ней углам.

Б. Два треугольника никогда не равны.

В. Два треугольника равны, если в одном треугольнике равна сторона

и два угла в другом треугольнике.

Г. Два треугольника равны, если в двух треугольниках равны по стороне

и по двум углам.

3). Один из вертикальных углов равен 40⁰. Чему равен другой угол?

А.40⁰ Б. 140⁰ В.180⁰ Г. невозможно вычислить

4). Выберите правильное утверждение:

А. Если односторонние углы равны, то две прямые параллельны

Б. Если соответственные углы равны, то две прямые параллельны

В. Если сумма соответственных углов равна 180⁰, то две прямые параллельны.

Г. Если сумма накрест лежащих углов равна 180⁰, то две прямые параллельны.

5). В равнобедренном треугольнике угол при вершине равен 70⁰ .Чему равны

остальные углы?

А.70⁰ и 70⁰ Б. 55⁰ и 55⁰ В. 70⁰ и 40⁰ Г. невозможно вычислить

В

6). Треугольник АВС- равнобедренный(АВ=ВС). ВD-медиана.

Угол АВD= 40⁰. Чему равны углы треугольника ВDС.

А С

D

А.40⁰ 90⁰ и 50⁰ Б. 45⁰, 45⁰ и 90⁰ В. 40⁰, 40⁰ и 100⁰ Г. невозможно вычислить

2 часть – решите задачи.

7). с По чертежу найдите угол 1, если

1 а известно, что а  в.

Запишите дано, найти, решение.

в

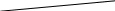46⁰

8). Параллельные прямые с и в пересечены двумя параллельными секущими АВ и СD, причем А и С принадлежат прямой с , В и D – прямой в .

Докажите, что АВ=СD.

СПЕЦИФИКАЦИЯ контрольно-измерительных материалов для проведения контрольных работ по геометрии в 8 классе

Контрольная работа №1 по теме «Четырехугольники»

Время выполнения: 40 минут

Цель: определение уровня образовательных достижений в усвоении содержания темы «Четырехугольники»

Содержание контрольных измерительных заданий

КИМ составлен в 2-х вариантах. Каждому учащемуся предоставляется распечатка заданий. Работа содержит две группы заданий, обязательных для выполнения всеми учащимися. Назначение первой группы – обеспечить проверку достижения учащимся уровня базовой подготовки, а второй – обеспечить проверку достижения повышенного уровня подготовки. В каждом варианте предоставляется дополнительное задание № 6 * на дополнительную отметку. Тип заданий: ВО – выбор ответа(часть 1), КО – краткий ответ(часть 2), РО – развернутый ответ(часть 3). Распределение заданий КИМ по уровню сложности

№		Что проверяется		Уровень		Баллы
	Тип задания	Предметный результат	Элемент содержания	Базовый	Повышенный
Задание 1	ВО	2.1	1.2, 1.1, 1.3	Б		1-3
Задание 2	КО	2.2, 2.4, 2.3	1.4. 1.5	Б		1
Задание 3	КО	2.3, 2.4	1.1, 1.4	Б		1
Задание 4	РО	2.4, 2.2	1.2, 1.9		П	2
Задание 5	РО	2.3	1.6		П	3
ИТОГО						10 баллов
Дополнительное задание (на дополнительную отметку) Задание 6*	РО	2.3, 2.4, 2.2	1.4, 1.7, 1.8		П	3

Система оценки выполнения отдельных заданий и работы в целом

%выполнения	Баллы	Отметка
90 – 100 %	9-10	Отметка «5»
70 – 89 %	7-8	Отметка «4»
50 – 69 %	5-6	Отметка «3»
Менее 50 %	Менее 5 баллов	Отметка «2»

Кодификатор элементов содержания и требований к уровню подготовки обучающихся

1. Перечень элементов предметного содержания

Код	Описание элементов предметного содержания
1.1	Параллелограмм, его свойства и признаки
1.2	Ромб, свойства и признаки.
1.3	Трапеция, свойства.
1.4	Периметр многоугольника.
1.5	Прямоугольник, свойства.
1.6	Центральная симметрия.
1.7	Равнобедренный треугольник, свойства.
1.8	Параллельность прямых. Накрест лежащие углы.
1.9	Сумма углов треугольника.

2. Перечень требований к уровню подготовки обучающихся

Код	Описание требований к уровню подготовки обучающихся
2.1.	Проводить доказательные рассуждения при решении задач, оценивать логическую правильность рассуждений, распознавать ошибочные заключения
2.2.	исследовать построенные модели с использованием геометрических понятий и теорем
2.3.	Распознавать геометрические фигуры на плоскости, различать их взаимное расположение, изображать геометрические фигуры; выполнять
	чертежи по условию задачи
2.4.	Решать планиметрические задачи на нахождение геометрических величин (длин, углов, периметра)

3. Перечень элементов метапредметного содержания

	Проверяемые элементы
1.	способности самостоятельно планировать альтернативные пути достижения целей, осознанно выбирать наиболее эффективные способы решения учебных и познавательных задач;
2.	способности адекватно оценивать правильность или ошибочность выполнения учебной задачи, её объективную трудность и собственные возможности её решения;
3.	умения устанавливать причинно-следственные связи; строить логические рассуждения, умозаключения (индуктивные, дедуктивные и по аналогии) и выводы;
4.	умения создавать, применять и преобразовывать знаково-символические средства, модели и схемы для решения учебных и познавательных задач;
5.	умения понимать и использовать математические средства наглядности (рисунки, чертежи, схемы и др.) для иллюстрации, интерпретации, аргументации;
6.	умения выдвигать гипотезы при решении учебных задач и понимания необходимости их проверки;
7.	понимания сущности алгоритмических предписаний и умения действовать в соответствии с предложенным алгоритмом;
8.	умения самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических проблем;
9.	способности планировать и осуществлять деятельность, направленную на решение задач исследовательского характера;

Контрольная работа №2 по теме "Подобные треугольники"

Тема: «Подобные треугольники»

Время выполнения: 40 минут

Цель: определение уровня образовательных достижений в усвоении содержания темы «Подобные треугольники»

Содержание контрольных измерительных заданий

КИМ составлен в 2-х вариантах. Каждому учащемуся предоставляется распечатка заданий. Работа содержит две группы заданий, обязательных для выполнения всеми учащимися. Назначение первой группы – обеспечить проверку достижения учащимся уровня базовой подготовки, а второй – обеспечить проверку достижения повышенного уровня подготовки. В каждом варианте предоставляется дополнительное задание № 6 * на дополнительную отметку. Тип заданий: ВО – выбор ответа(часть 1), КО – краткий ответ(часть 2), РО – развернутый ответ(часть 3). Распределение заданий КИМ по уровню сложности

№		Что проверяется		Уровень		Баллы
	Тип задания	Предметный результат	Элемент содержания	Базовый	Повышенный
Задание 1	ВО	2.1	1.1	Б		1
Задание 2	ВО	2.1, 2.2, 2.3	1.2, 1.3, 1.4	Б		1
Задание 3	КО	2.3, 2.1	1.4	Б		2
Задание 4	КО	2.1, 2.3, 2.2	1.2, 1.5, 1.6	Б		2
Задание 5	РО	2.3	1.4		П	3
ИТОГО						9 баллов
Дополнительное задание (на дополнительную отметку) Задание 6*	РО	2.1, 2.2, 2.3, 2.4	1.4, 1.1, 1.7		П	3

Система оценки выполнения отдельных заданий и работы в целом

%выполнения	Баллы	Отметка
90 – 100 %	8-9	Отметка «5»
70 – 89 %	6-7	Отметка «4»
50 – 69 %	4-5	Отметка «3»
Менее 50 %	Менее 4 баллов	Отметка «2»

Кодификатор

элементов содержания и требований к уровню подготовки обучающихся

4. Перечень элементов предметного содержания

Код	Описание элементов предметного содержания
1.1	Синус, косинус, тангенс острого угла прямоугольного треугольника
1.2	Прямоугольный треугольник, свойства. Теорема Пифагора
1.3	Средняя линия треугольника.
1.4	Подобие треугольников, коэффициент подобия. Признаки подобия треугольников
1.5	Равнобедренный треугольник, свойства.
1.6	Сумма углов в треугольнике.
1.7	Перпендикулярность прямых.

5. Перечень требований к уровню подготовки обучающихся

Код	Описание требований к уровню подготовки обучающихся
2.1.	Решать планиметрические задачи на нахождение геометрических величин (длин, углов, площадей)
2.2.	Распознавать геометрические фигуры на плоскости, различать их взаимное расположение, изображать геометрические фигуры; выполнять чертежи по условию задачи
2.3.	Проводить доказательные рассуждения при решении задач, оценивать логическую правильность рассуждений, распознавать ошибочные заключения
2.4.	Описывать реальные ситуации на языке геометрии, исследовать
	построенные модели с использованием геометрических понятий и теорем, решать практические задачи, связанные с нахождением геометрических величин

6. Перечень элементов метапредметного содержания

	Проверяемые элементы
10.	способности самостоятельно планировать альтернативные пути достижения целей, осознанно выбирать наиболее эффективные способы решения учебных и познавательных задач;
11.	способности адекватно оценивать правильность или ошибочность выполнения учебной задачи, её объективную трудность и собственные возможности её решения;
12.	умения устанавливать причинно-следственные связи; строить логические рассуждения, умозаключения (индуктивные, дедуктивные и по аналогии) и выводы;
13.	умения создавать, применять и преобразовывать знаково-символические средства, модели и схемы для решения учебных и познавательных задач;
14.	умения понимать и использовать математические средства наглядности (рисунки, чертежи, схемы и др.) для иллюстрации, интерпретации, аргументации;
15.	умения выдвигать гипотезы при решении учебных задач и понимания необходимости их проверки;
16.	понимания сущности алгоритмических предписаний и умения действовать в соответствии с предложенным алгоритмом;
17.	умения самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических проблем;
18.	способности планировать и осуществлять деятельность, направленную на решение задач исследовательского характера;

Контрольная работа №3 по теме "Площадь"

Время выполнения: 40 минут

Цель: определение уровня образовательных достижений в усвоении содержания темы «Площадь»

Содержание контрольных измерительных заданий

КИМ составлен в 2-х вариантах. Каждому учащемуся предоставляется распечатка заданий. Работа содержит две группы заданий, обязательных для выполнения всеми учащимися. Назначение первой группы – обеспечить проверку достижения учащимся уровня базовой подготовки, а второй – обеспечить проверку достижения повышенного уровня подготовки. Тип заданий: ВО – выбор ответа(часть 1), КО – краткий ответ(часть 2), РО – развернутый ответ(часть 3).

Распределение заданий КИМ по уровню сложности

№		Что проверяется				Балл
	Тип задания	Предметный результат	Элеменсодержания	Базовый	Повышенный
Задание 1	ВО	2.1,	1.1	Б		1
Задание 2	КО	2.1, 2.3	1.2	Б		2
Задание 3	РО	2.5, 2.3	1.2, 1.3, 1.4, 1.8	Б		2
Задание 4	РО	2.5, 2.3, 2.1	1.5, 1.6, 1.2, 1.7		П	3
Задание 5	РО	2.1, 2.3, 2.2	1.7, 1.1, 1.2,		П	3
ИТОГО						11 баллов

Система оценки выполнения отдельных заданий и работы в целом

%выполнения	Баллы	Отметка
90 – 100 %	10-11	Отметка «5»
70 – 89 %	8-9	Отметка «4»
50 – 69 %	5-7	Отметка «3»
Менее 50 %	Менее 5 баллов	Отметка «2»

Кодификатор

элементов содержания и требований к уровню подготовки обучающихся

7. Перечень элементов предметного содержания

Код	Описание элементов предметного содержания
1.1	Площадь треугольника.
1.2	Прямоугольный треугольник. Теорема Пифагора.
1.3	Равнобедренный треугольник, свойства.
1.4	Высота, медиана, биссектриса треугольника.
1.5	Площадь трапеции.
1.6	Признаки равенства треугольников.
1.7	Прямоугольник и его свойства.
1.8	Ромб и его свойства.

1. Перечень требований к уровню подготовки обучающихся

Код	Описание требований к уровню подготовки обучающихся
2.1.	Решать планиметрические задачи на нахождение геометрических величин (длин, площадей)
2.2.	Проводить доказательные рассуждения при решении задач, оценивать логическую правильность рассуждений, распознавать ошибочные заключения
2.3.	Описывать реальные ситуации на языке геометрии, исследовать построенные модели с использованием геометрических понятий и теорем, решать практические задачи, связанные с нахождением геометрических величин
2.4	Распознавать геометрические фигуры на плоскости, различать их взаимное расположение, изображать геометрические фигуры; выполнять чертежи по условию задачи

1. Перечень элементов метапредметного содержания

	Проверяемые элементы
19.	способности самостоятельно планировать альтернативные пути достижения целей, осознанно выбирать наиболее эффективные способы решения учебных и познавательных задач;
20.	способности адекватно оценивать правильность или ошибочность выполнения учебной задачи, её объективную трудность и собственные возможности её решения;
21.	умения устанавливать причинно-следственные связи; строить логические рассуждения, умозаключения (индуктивные, дедуктивные и по аналогии) и выводы;
22.	умения создавать, применять и преобразовывать знаково-символические средства, модели и схемы для решения учебных и познавательных задач;
23.	умения понимать и использовать математические средства наглядности (рисунки, чертежи, схемы и др.) для иллюстрации, интерпретации, аргументации;
24.	умения выдвигать гипотезы при решении учебных задач и понимания необходимости их проверки;
25.	понимания сущности алгоритмических предписаний и умения действовать в соответствии с предложенным алгоритмом;
26.	умения самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических проблем;
27.	способности планировать и осуществлять деятельность, направленную на решение задач исследовательского характера;

Контрольная работа по теме "Теорема Пифагора и начала тригонометрии"

Цель: проверить уровень усвоения ФГОС:

• знания и умения применять при решении задач теорему Пифагора

• знание и умение применять при решении задач определения синуса, косинуса острого угла прямоугольного треугольника;

• виды треугольников (равнобедренный, равносторонний) и их свойства;

• виды трапеций и их свойства;

• свойства диагоналей ромба;

• умение выполнять чертеж по условию задачи;

• умение оформлять решение задачи.

Характеристика структуры и содержания работы Работа по геометрии состоит из 3-х частей:

• Уровень А включает 2 задания, которые позволяют выявить знания и умения на базовом уровне.

• Уровень В включает 2 задания, которые позволяют выявить знания и умения на базовом уровне с полным решением геометрической задачи;

• Уровень С включает 2 задания, которые позволяют выявить умения и навыки выполнения заданий на применение знаний и умений, способов деятельности в изменённой ситуации и в незнакомой ситуации.

Работа по геометрии состоит 6 заданий, которые позволяют выявить знания и умения на базовом уровне.

На выполнение работы отводится 40 минут.

Распределение заданий по содержанию и уровню сложности

Содержательная линия	Воспроиз- ведение знаний	Примене- ние знаний	Интеграция знаний	Процентное соотношение в тексте
Найти гипотенузу треугольника	№1			10 %
Найти периметр треугольника	№2			10 %
Найти диагональ (сторону) ромба		№3		20 %
Найти основание равнобедренного треугольника		№4		20 %
Найти расстояние от точки до прямой			№5	20 %
Найти высоту описанной трапеции			№6	20 %
Процентное соотношение заданий	20 %	40 %	40 %	100 %

Спецификация заданий и критерии оценивания

№ зада ния	Характеристика задания	Проверяемые элементы	Балл за выполнение проверяемо-	Балл за вы- полнение задания
			го элемента
1	Найти гипотенузу треугольника	Знание теоремы Пифагора.	1 балл	2 балла
		Умение применять теорему Пифагора.	1 балл
2	Найти периметр треугольника	Знание теоремы Пифагора.	1 балл	2 балла
		Умение применять теорему Пифагора.	1 балл
3	Найти диагональ (сторону) ромба	Выполнение чертежа по условию задачи.	1 балл	3 балла
		Умение применять теорему Пифагора.	1 балл
		Оформление решения задачи.	1 балл
4	Найти основание равнобедренного треугольника	Выполнение чертежа по условию задачи.	1 балл	3 балла
		Уметь применять свойства равнобедренного треугольника	1 балл
		Оформление решения задачи.	1 балл
5	Найти расстояние от точки до прямой	Выполнение чертежа по условию задачи.	1 балл	3 балла
		Умение применять теорему Пифагора	1 балл
		Оформление решения задачи.	1 балл
6	Найти высоту описанной трапеции	Выполнение чертежа по условию задачи.	1 балл	4 балла
		Умение применять свойство равнобокой трапеции	1 балл
		Оформление решения задачи.	1 балл
		Выбор оптимального решения	1 балл

Максимальный балл за работу -17

Шкала пересчёта первичного балла за выполнение контрольной работы вотметку по пятибалльной шкале

Отметка по пятибалльной шкале	«2»	«3»	«4»	«5»
Общий балл	0 – 7	8 - 12	13 – 14	15 - 17
% выполнения работы	Менее 50%	50 – 69%	70 -89%	90 – 100%

Контрольная работа по теме "Углы в окружности. Вписанные и описанные четырехугольники"

Время выполнения: 40 минут

Цель: определение уровня образовательных достижений в усвоении содержания темы «Окружность»

Содержание контрольных измерительных заданий

КИМ составлен в 2-х вариантах. Каждому учащемуся предоставляется распечатка заданий. Работа содержит две группы заданий, обязательных для выполнения всеми учащимися. Назначение первой группы – обеспечить проверку достижения учащимся уровня базовой подготовки, а второй – обеспечить проверку достижения повышенного уровня подготовки. В каждом варианте предоставляется дополнительное задание № 6 * на дополнительную отметку. Тип заданий: ВО – выбор ответа(часть 1), КО – краткий ответ(часть 2), РО – развернутый ответ(часть 3). Распределение заданий КИМ по уровню сложности

№		Что проверяется		Уровень		Бал
	Тип задания	Предметный результат	Элем	Базовый	П
Задание 1	ВО	2.1	1.1, 1.2, 1.3	Б		1
Задание 2	ВО	2.1	1.2, 1.4	Б		1
Задание 3	КО	2.1, 2.2, 2.3	1.4, 1.5, 1.6	Б		2
Задание 4	КО	2.1, 2.2	1.7	Б		2
Задание 5	РО	2.1, 2.4, 2.3	1.8, 1.9		П	3
ИТОГО						9
Дополнительное задание Задание 6*	РО	2.1, 2.4, 2.3	1.3, 1.10		П	3

Система оценки выполнения отдельных заданий и работы в целом

%выполнения	Баллы	Отметка
90 – 100 %	8-9	Отметка «5»
70 – 89 %	6-7	Отметка «4»
50 – 69 %	4-5	Отметка «3»
Менее 50 %	Менее 4 баллов	Отметка «2»

Кодификатор

элементов содержания и требований к уровню подготовки обучающихся

10. Перечень элементов предметного содержания

Код	Описание элементов предметного содержания
1.1	Биссектриса угла.
1.2	Сумма углов в треугольнике.
1.3	Касательная и секущая к окружности; свойства касательных, проведённых из одной точки к окружности.
1.4	Центральный, вписанный угол; величина вписанного угла.
1.5	Окружность, описанная около прямоугольного треугольника.
1.6	Прямоугольный треугольник. Теорема Пифагора.
1.7	Свойство хорд окружности.
1.8	Свойство высоты, проведенной на гипотенузу в прямоугольном треугольнике.
1.9	Прямоугольный треугольник. Теорема Пифагора.
1.10	Равнобедренный треугольник, свойства.

1. Перечень требований к уровню подготовки обучающихся

Код	Описание требований к уровню подготовки обучающихся
2.1.	Решать планиметрические задачи на нахождение геометрических величин (длин, углов)
2.2.	Распознавать геометрические фигуры на плоскости, различать их взаимное расположение, изображать геометрические фигуры; выполнять чертежи по условию задачи
2.3.	Проводить доказательные рассуждения при решении задач, оценивать логическую правильность рассуждений, распознавать ошибочные заключения
2.4.	Описывать реальные ситуации на языке геометрии, исследовать
	построенные модели с использованием геометрических понятий и теорем, решать практические задачи, связанные с нахождением геометрических величин

1. Перечень элементов метапредметного содержания

	Проверяемые элементы
28.	способности самостоятельно планировать альтернативные пути достижения целей, осознанно выбирать наиболее эффективные способы решения учебных и познавательных задач;
29.	способности адекватно оценивать правильность или ошибочность выполнения учебной задачи, её объективную трудность и собственные возможности её решения;
30.	умения устанавливать причинно-следственные связи; строить логические рассуждения, умозаключения (индуктивные, дедуктивные и по аналогии) и выводы;
31.	умения создавать, применять и преобразовывать знаково-символические средства, модели и схемы для решения учебных и познавательных задач;
32.	умения понимать и использовать математические средства наглядности (рисунки, чертежи, схемы и др.) для иллюстрации, интерпретации, аргументации;
33.	умения выдвигать гипотезы при решении учебных задач и понимания необходимости их проверки;
34.	понимания сущности алгоритмических предписаний и умения действовать в соответствии с предложенным алгоритмом;
35.	умения самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических проблем;
36.	способности планировать и осуществлять деятельность, направленную на решение задач исследовательского характера;

Контрольная работа итоговая за курс 8 класса

1. Назначение итоговой работы - определить уровень достижения учащимися предметных планируемых результатов по всем изученным темам за год, а также выявить уровень достижения метапредметных результатов. Каждое задание базового уровня в диагностической работе оценивает конкретный предметный планируемый результат, задания повышенного уровня сложности позволяют оценить и предметные, и метапредметные планируемые результаты.

Планируемые результаты: Проверить уровень достижения результатов по основным темам курса геометрии 8 класса для обеспечения возможности успешного продолжения образования на базовом уровне.

Критерии оценивания диагностической работы

Максимальный балл за выполнение работы составляет – 13 баллов. На основе баллов, выставленных за выполнение всех заданий работы, подсчитывается первичный балл, который переводится в отметку по пятибалльной шкале (таблица 1).

Таблица 1

Перевод баллов в отметку по пятибалльной шкале

Процент выполнения от максимального балла	Количество баллов	Цифровая отметка	Уровневая шкала
92-100	12-13	5	Повышенный
69-91	9-11	4
46-68	6-8	3	Базовый
Менее 46	Менее 6	2	Недостаточный

Продолжительность работы

Продолжительность диагностической работы 40 минут.

Распределение заданий по разделам программ(ы)

№ п/п	Раздел программы (содержательная линия)	Количество заданий базового уровня сложности	Количество заданий повышенного уровня сложности
1.	Геометрические фигуры	2	1
2.	Измерения и вычисления	4	1
3.	Отношения	1	1
	Всего	7	3

План диагностической работы

№	Раздел программы (содержательная линия)	Проверяемый планируемый результат			Уровень сложности	Тип задания	t	Максимальный балл
1	Измерения и вычисления Четырехугольники	применять для решения задач геометрические факты, если условия их применения заданы в явной форме			Базовый	Со свободным, кратким однозначным ответом	3	1 балл
2	Отношения. Подобие треугольников	оперировать на базовом уровне понятием подобие фигур			Базовый	Со свободным, кратким однозначным ответом	3	1 балл
3	Измерения и вычисления. Определение тригонометрических функций	применять базовые тригонометрические соотношения для вычисления длин, расстояний, площадей в простейших случаях			Базовый	Со свободным, кратким однозначным ответом	3	1 балл
4	Геометрические фигуры. Вписанный угол			решать задачи на нахождение геометрических величин по образцам или алгоритмам.	Базовый	Со свободным, кратким однозначным ответом	3	1 балл
5	Измерения вычисления Прямоугольный треугольник	и		решать задачи на нахождение геометрических величин по образцам или алгоритмам.	Базовый	Со свободным, кратким однозначным ответом	3	1 балл
6	Измерения и вычисления. Хорды окружности			решать задачи на нахождение геометрических величин по образцам или алгоритмам.	Базовый	Со свободным, кратким однозначным ответом	3	1 балл
7	Геометрические фигуры			оперировать на базовом уровне понятиями	Базовый	Со свободным, кратким однозначным ответом	3	1 балл
8	Измерения вычисления. Теорема Пифагора	и		применять теорему Пифагора, для вычисления длин и hасстояний в простейших случаях применять геометрические факты для решения задач, в ом числе, предполагающих несколько шагов решения	Повышенный	С развернутым ответом	6	2 балла
9	Отношения.			доказывать геометрические утверждения применять геометрические факты для решения задач, в том числе, предполагающих несколько шагов решения	Повышенный	С развернутым ответом	6	2 балла
10	Геометрические фигур. Свойсво отрезков касательных		доказывать геометрические утверждения применять геометрические факты для решения задач, в том числе, предполагающих несколько шагов решения		Повышенный	С развернутым ответом	7	2 балла
							40 мин	13 баллов

Инструкция по проверке и оценке работ

№ задания	Планируемый результат	Правильный ответ		Критерии
		Вариант1	Вариант2	Макc
1	Решение задачи на вычисление сторон параллелограмма	16,2	20	1 б
2	Решение задач на применение подобия	300	56	1 б
3	Нахождение элементов треугольника с использованием тригонометрических функций	0,6	0,8	1 б
4	Вычисление углов, связанных с окружностью	42	155	1 б
5	Решение задачи на применение формулы площади треугольника	9,2	7,2	1
6	Решение задачи на применение свойств хорд	8	3	1 б
7	Анализ геометрических высказываний.	14	12	1 б
8	Решение задачи на применение признаков теоремы Пифагора	12	9	2
9	Решение задачи с применением свойств биссектрисы угла			2
10	Решение задачи на применение свойств отрезков касательных	5	24	2,

Итоговая работа 8 класс

Фамилия____________________________ Имя__________________________ класс_______________ школа__________________________________________

ВариантI

1 часть

В каждом задании первой части необходимо записать верный ответ, в отведенном для этого месте. Каждый верный ответ оценивается в один балл.

1. Периметр параллелограмма равен 36, а одна из его сторон в 9 раз больше другой. Найдите длину большей стороны.

Ответ:______________________

1. В селе Париж Челябинской области находится мачта сотовой связи, выполненная в виде Эйфелевой башни. Южноуральская «Эйфелева башня» в шесть раз меньше настоящей. Эйфелева башня в Париже весит 8 000 000 кг. Найдите высоту Эйфелевой башни в Париже, если высота башни, установленной в селе Париж равна 50 м.

Ответ:______________________

1. П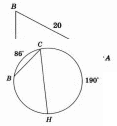 о данным рисунка найдите синус угла А.

Ответ:______________________

1. По данным рисунка найдите градусную меру угла ВСН.

Ответ: ___________________________

1. В прямоугольном треугольнике катеты равны 10 и 24. Найдите высоту, проведенную к гипотенузе этого треугольника. Ответ округлите до десятых.

Ответ: ___________________________

1. Хорды АВ и КМ пересекаются в точке Р. Найдите длину отрезка ВР, если КР=4, АР=3, РМ=6.

Ответ: _______________________

1. Укажите номера верных утверждений.

1. Диагонали прямоугольника равны.

2. Сумма противоположных углов параллелограмма равна 180°.

3. Около любого параллелограмма можно описать окружность.

4. В любой треугольник можно вписать окружность. Ответ:______________________

II часть

Для записи решений и ответов каждого задания второй части используйте тетрадные листы в клетку. Запишите номер выполняемого задания, затем полное обоснованное решение и ответ. Каждое задание второй части оценивается от нуля до двух баллов.

1. Высота АН ромба АВСD делит сторону СD на отрезки DН=16 и СН=4. Найдите высоту ромба.

2. В трапеции АВСD биссектрисы углов В и С пересекаются в точке О, лежащей на стороне AD. Докажите, что точка О равноудалена от прямых АВ, ВС, CD.

3. Радиус окружности, вписанной в прямоугольный треугольник, равен 1. Периметр треугольника равен 12. Вычислите гипотенузу

треугольника.

9 класс ГЕОМЕТРИЯ

Контрольная работа №1 по теме "Решение треугольников"

Цель: проверить уровень усвоения ФГОС:

• знания и умения применять при решении задач теоремы синусов и косинусов, решать задачи на нахождение неизвестных элементов в треугольнке;

• умение оформлять решение задачи.

I вариант.

В треугольнике АВС B=350, =250. Укажите наибольшую сторону треугольника. Ответ объясните. Две стороны треугольника равны 3см и 8см, а угол между ними равен 600. Т Найдите периметр треугольника. . Решите треугольник АВС, если B=750, A=450, АВ=2 см Диагонали параллелограмма равны 12см и 20см, а угол между ними равен 600. Найдите стороны параллелограмма. В прямоугольном треугольнике один из углов равен α, а катет, прилежащий к данному углу, равен а. Найдите биссектрису прямого угла.

II вариант. В треугольнике АВС угол В=550, угол А=1100. Укажите наименьшую сторону треугольника. Ответ объясните. Две стороны треугольника равны 3см и 5см, а угол между ними равен 1200. Найдите периметр треугольника. Решите треугольник АВС, если угол В=300, угол С=1050, АС=4см. Стороны параллелограмма равны 10см и 16см, а угол между ними равен 600 . Найдите диагонали параллелограмма. 5. В прямоугольном треугольнике гипотенуза равна с, а один из острых углов равен β. Найдите биссектрису второго острого угла.

Распределение заданий по содержанию и уровню сложности

Содержательная линия	Воспроиз- ведение знаний	Примене- ние знаний	Интеграция знаний	Процентное соотношение в тексте
Теорема синусов	№1,		№5	40%
Теорема косинусов	№2	№4		40%
Решение треугольника		№3		20%
Процентное соотношение заданий	40 %	40 %	20 %	100 %

Спецификация заданий и критерии оценивания

№ зада ния	Характеристика задания	Проверяемые элементы	Балл за выполнение проверяемо- го элемента	Балл за вы- полнение задания
1	Теорема синусов.	Нахождение угла треугольника.	1 балл	3 балла
		Знание следствия из теоремы синусов.	1 балл
		Запись ответа.	1 балл
2	Теорема косинусов.	Знание теоремы косинусов.	1 балл	4 балла
		Умение находить периметр.	1 балл
		Вычисления.	1 балл
		Оформление решения задачи.	1 балл
3	Решение треугольника.	Нахождение угла треугольника.	1 балл	5 баллов
		Применение теоремы синусов.	2 балла
		Вычисления.	1 балл
		Оформление решения задачи.	1 балл
4	Теорема косинусов.	Определение неизвестных элементов.	1 балл	5 баллов
		Нахождение катета.	1 балл
		Нахождение острых углов.	1 балл
		Вычисления.	1 балл
		Оформление решения задачи.	1 балл
5	Теорема синусов.	Выполнение чертежа по условию задачи.	1 балл	5 баллов
		Применение определения биссектрисы.	1 балл
		Нахождение угла.	1 балл
		Нахождение биссектрисы.	1 балл
		Оформление решения задачи.	1 балл

Критерии оценивания:

1-10 баллов – «2»

11-15 баллов – «3» 16-20 баллов – «4»

21-22 балла – «5»

Контрольная работа №2 по теме "Преобразование подобия. Метрические соотношения в окружности"

Цель: проверить степень усвоения учащимися данной темы. Проверить умение

учащихся применять изученный материал на практике

Время проведения: 40 минут

Форма проведения: контрольная работа

Текст Контрольная работа № 2

На тему: Преобразование подобия. Метрические соотношения в окружности.

1. Отрезок ВК-биссектриса угла В треугольника АВС. Найдите сторону АС , если АВ:ВС=2:3, СК-АК=3 см.

2. При пересечении двух хорд одна из них делится на отрезки 20 см и 4 см, а вторая – на отрезки, один из которых меньше другого на 2 см . Найти длину второй хорды.

3. Из точки А к окружности проведены касательная АК=4 см и секущая АЕ=8 см. Найдите длину отрезка АF секущей , лежащего вне окружности.

4. Продолжения боковых сторон АВ и СД трапеции АВСД пересекаются в точке М, AB:BМ=3:7, AD- большее основание трапеции. Найдите основания трапеции, если их разность равна 6 см.

Распределение заданий по содержанию и уровню сложности

Содержательная линия	Воспроиз- ведение знаний	Примене- ние знаний	Интеграция знаний	Процентное соотношение в тексте
Координаты вектора и его абсолютная величина.	№1,			20 %
Действия с векторами. Геометрический смысл.	№2			20%
Условия перпендикулярности и коллинеарности векторов.		№3		20%
Скалярное произведение и его		№4	№5	40 %
свойства.
Процентное соотношение заданий	40 %	40 %	20 %	100 %

Спецификация заданий и критерии оценивания

№ зада ния	Характеристика задания	Проверяемые элементы	Балл за выполнение проверяемо- го элемента	Балл за вы- полнение задания
1	Координаты вектора и его абсолютная величина.	Формула нахождения координат вектора.	1 балл	3 балла
		Формула абсолютной величины.	1 балл
		Вычисления.	1 балл
2	Действия с векто- рами. Геометричес- кий смысл.	Правило треугольника.	1 балл	3 балла
		Правило параллелограмма.	1 балл
		Правило многоугольника.	1 балл
3	Условия перпенди- кулярности и кол- линеарности векторов.	Условие коллинеарности векторов и вычисление .	2 балла	5 баллов
		Условие перпендикулярности векторов и вычисления.	2 балла
		Оформление решения задачи.	1 балл
4	Нахождение косинуса угла между векторами.	Нахождение координат вектора.	1 балл	5 баллов
		Знание формулы нахождения косинуса угла между векторами.	1 балл
		Нахождение абсолютной величины.	1 балл
		Вычисление по формуле.	1 балл
		Оформление решения задачи.	1 балл
5	Скалярное произведение и его свойства.	Скалярный квадрат.	2 балла	5 баллов
		ФСУ.	1 балл
		Вычисление.	1 балл
		Оформление решения задачи.	1 балл

Критерии оценивания:

1-10 баллов – «2»

11-15 баллов – «3» 16-19 баллов – «4»

20-21 балл – «5»

Кодификатор элементов содержания и требований к уровню подготовки обучающихся для проведения контрольной работы №5 по теме «Декартовы координаты на плоскости. Движение»

Тема: Декартовы координаты на плоскости. Движение»

1. Перечень элементов предметного содержания, проверяемых на контрольной работе.

Код	Описание элементов предметного содержания
1.1	Декартовы координаты на плоскости; координаты точки. Координаты середины отрезка. Формула расстояния между двумя точками плоскости.
1.2	Параллелограмм и его свойства
1.3	Уравнение окружности с центром в начале координат
1.4	Трапеция. Средняя линия трапеции. Равнобедренная трапеция
1.5	Ромб. свойства ромба.

1. Перечень требований к уровню подготовки обучающихся, освоивших тему Декартовы координаты на плоскости. Движение»

Код	Описание требований к уровню подготовки обучающихся.
2.1	уметь решать геометрические задачи, опираясь на изученные свойства фигур и отношений между ними, применяя дополнительные построения ,алгебраический и тригонометрический аппарат, соображения симметрии
2. 2	Проводить доказательные рассуждения при решении задач, используя известные теоремы, обнаруживая возможности для их использования, выстраивать аргументации при доказательстве; распознавать логически некорректных рассуждений; записывать математические утверждения, доказательства
2. 3	Уметь выполнять расчёты по формулам.

Назначение контрольной работы: оценить уровень освоения каждым учащимся класса содержания учебного материала по теме Декартовые координаты на плоскости. Движение»

Содержание контрольных измерительных заданий определяется содержанием рабочей программы по теме Декартовые координаты на плоскости. Движение»

Контрольная работа состоит из 7 заданий: 5 задания базового уровня, 2 повышенного.

Распределение заданий по уровням сложности, проверяемым элементам , уровню подготовки, типам заданий и времени выполнения представлено в таблице. Таблица1.

№ задания	уровень	Что проверяется	Тип задания	Примерное Время выполнения задания
1	Базовый	Код из кодификатора 1.1 1.5	Развёрнутый ответ	8мин
2	Базовый	Код из кодификатора 1.2 1.3	Развёрнутый ответ	10мин
3	повышенный	1.2 1.4	Подробное решение	12
4	повышенный	1.1 1.4	Развёрнутый ответ	15

На выполнение 4 заданий отводиться 40 минут. Задания в контрольной работе оцениваются в зависимости от сложности задания разным количеством баллов, указанных в таблице

№ задания	Количество баллов
1	Максимальное количество баллов -4
2	Максимальное количество баллов 5
3	Максимальное количество баллов 5
4	Максимальное количество баллов 6
итого	20баллов

Перевод баллов к 5-бальной отметке представлен в таблице

Баллы	отметка
_17- 20 баллов 85-100%	Отметка «5»
_13- 16 баллов 75-84%	Отметка «4»
9-12баллов 50-74%	Отметка «3»
1 - 8_ баллов менее 50%	Отметка «2»
баллов	Отметка «1»

Контрольная работа Итоговая

Цель: контрольная работа проводится с целью установления фактического уровня теоретических знаний учащихся по предмету геометрия, их практических умений и навыков, установления соответствия предметных учебных действий обучаемых требованиям ФГОС ООО

1. Назначение контрольной работы по геометрии: оценить уровень общеобразовательной подготовки обучающихся 9-х классов

2. Документы, определяющие содержание КИМ

Содержание контрольно-измерительного материала (далее – КИМ) определяет Федеральный государственный образовательный стандарт основного общего образования (далее – ФГОС).

1). Работа составлена в соответствии с Федеральным компонентом государственного стандарта основного общего образования по математике.

2).Учебник: Геометрия.7-9 классы: учеб.для общеобразоват.оранизаций/Л.С.Атанасян, В.Ф.Бутузов, С.Б.Кадомцев и др.-М.:Просвещение, 2017.

1. Подходы к отбору содержания

Проверяемое в контрольной работе содержание не выходит за рамки ФГОС и укладывается в рамки Фундаментального ядра содержания образования.

1. Связь КИМ контрольной работы с КИМ ОГЭ и ЕГЭ

Эта связь проявляется в отборе контролируемого содержания и построении структуры вопросов (с выбором одного верного ответа из нескольких, задания на решения уравнений, решение задач с обоснованием ответа).

1. Характеристика структуры и содержания КИМ

Работа включает 8 заданий: 5 заданий базового уровня сложности, 3 задания- повышенного уровня (задания с развернутым, обоснованным ответом).

Работа включает 2 варианта.

1. Распределение заданий КИМ по содержанию и проверяемым умениям и способам деятельности

№ вопроса	Элемент содержания, проверяемый заданиями КР	Код контролируемого элемента	Требования к уровню подготовки	Код требования
1	Сумма углов треугольника. Внешние углы треугольника	7.2.6	Решать планиметрические задачи на нахождение геометрических величин (длин, углов, площадей) Распознавать геометрические фигуры на плоскости, различать их взаимное расположение, изображать геометрические фигуры; выполнять чертежи по условию задачи	5.1 5.2
1	Высота, медиана, биссектриса, средняя линия треугольника; точки пересечения серединных перпендикуляров, биссектрис, медиан, высот или их продолжений	7.2 7.2.1	Решать планиметрические задачи на нахождение геометрических величин (длин, углов, площадей) Распознавать геометрические фигуры на плоскости, различать их взаимное расположение, изображать геометрические фигуры; выполнять чертежи по условию задачи	5.1 5.2
2	Окружность и круг	7.4	Решать планиметрические задачи на нахождение геометрических величин (длин, углов, площадей)	5.1
3	Площадь и её свойства. Площадь трапеции	7.5.6	Решать планиметрические задачи на нахождение геометрических величин (длин, углов, площадей) Распознавать геометрические фигуры на плоскости, различать их взаимное расположение, изображать геометрические фигуры; выполнять чертежи по условию задачи	5.1 5.2
4	Синус, косинус, тангенс острого угла прямоугольного треугольника и углов от 0о до 180о	7.2.10	Решать планиметрические задачи на нахождение геометрических величин (длин, углов, площадей) Распознавать геометрические фигуры на плоскости, различать их взаимное расположение, изображать геометрические фигуры; выполнять чертежи по условию задачи	5.1 5.2
5	Вписанные и описанные окружности правильного многоугольника Сумма углов выпуклого многоугольника	7.4.6 7.3.4	Решать планиметрические задачи на нахождение геометрических величин (длин, углов, площадей) Распознавать геометрические фигуры на плоскости, различать их взаимное расположение, изображать геометрические фигуры; выполнять чертежи по условию задачи	5.1 5.2
6	Трапеция, средняя линия трапеции; равнобедренная трапеция	7.3.3	Решать планиметрические задачи на нахождение геометрических величин (длин, углов, площадей) Распознавать геометрические фигуры на плоскости, различать их взаимное расположение, изображать геометрические фигуры; выполнять чертежи по условию задачи	5.1 5.2
7	Равнобедренный и равносторонний треугольники. Свойства и признаки равнобедренного треугольника	7.2.2	Решать планиметрические задачи на нахождение геометрических величин (длин, углов, площадей) Распознавать геометрические фигуры на плоскости, различать их взаимное расположение, изображать геометрические фигуры; выполнять чертежи по условию задачи Проводить доказательные рассуждения при решении задач, оценивать логическую правильность рассуждений, распознавать ошибочные заключения	5.1 5.2 7.8
8	Высота, медиана, биссектриса, средняя линия треугольника; точки пересечения серединных перпендикуляров, биссектрис, медиан, высот или их продолжений Прямоугольный треугольник. Теорема Пифагора Окружность и круг	7.2.1 7.2.3 7.4	Решать планиметрические задачи на нахождение геометрических величин (длин, углов, площадей) Распознавать геометрические фигуры на плоскости, различать их взаимное расположение, изображать геометрические фигуры; выполнять чертежи по условию задачи Проводить доказательные рассуждения при решении задач, оценивать логическую правильность рассуждений, распознавать ошибочные заключения	5.1 5.2 7.8

Контрольная работа проводится в соответствии с тематическим планированием рабочей программы.

1. Система оценивания

№ задания	Балл	Сумма
1	1	1
2	1	1
3	1	1
4	1	1
5	1	1
6	2	2
7	2	2
8	3	3
Итого:		12

0-4б.-«2»

5-7б.-«3»

8-10б.-«4»

11-12б.-«5»

Ответы

№ задания	1	2	3	4	5	6	7	8
В1	98	60	33	1,5	1	9	Задача на доказательство	6
В2	24	123	42	3	2	10	Задача на доказательство	2

1. Форма представления результатов: анализ результатов в модуле МСОКО АИС «СГО».

2. Текст работы

Текст итоговой контрольной работы по геометрии (9 класс) с решениеями

Вариант1

1. 

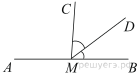
На прямой AB взята точка M. Луч MD — биссектриса угла CMB. Известно, что ∠DMC = 41°. Найдите угол CMA. Ответ дайте в градусах.

2. 

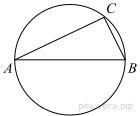
Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Найдите угол ABC, если угол BAC равен 30°. Ответ дайте в градусах.

3. 

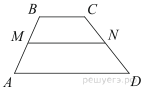
В трапеции ABCD известно, что AD = 7, BC = 5, а её площадь равна 72. Найдите площадь трапеции BCNM, где MN – средняя линия трапеции ABCD.

 

4. 

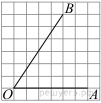
Найдите тангенс угла  , изображённого на рисунке.

5. 

Какое из следующих утверждений верно?

1) Сумма углов выпуклого четырёхугольника равна 360 градусам.

2) Средняя линия трапеции равна сумме её оснований.

3) Любой параллелограмм можно вписать в окружность.

6. 

Основания трапеции равны 16 и 34. Найдите отрезок, соединяющий середины диагоналей трапеции.

7. 

В остроугольном треугольнике ABC проведены высоты   и   Докажите, что углы   и   равны.

8. 

Медиана BM треугольника ABC равна 3 и является диаметром окружности, пересекающей сторону BC в её середине. Найдите диаметр описанной окружности треугольника ABC.

Вариант2

1. 

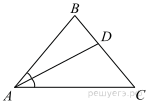
В треугольнике   известно, что  ,   — биссектриса. Найдите угол  . Ответ дайте в градусах.

2. 

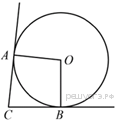В угол C величиной 57° вписана окружность, которая касается сторон угла в точках A и B, точка O - центр окружности. Найдите угол AOB. Ответ дайте в градусах.

.

3. 

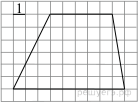Найдите площадь трапеции, изображённой на рисунке.

4. 

Найдите тангенс угла  , изображённого на рисунке.

 

5. 

Какое из следующих утверждений верно?

 

1) Диагонали параллелограмма равны.

2) Площадь ромба равна произведению его стороны на высоту, проведённую к этой стороне.

3) Если две стороны и угол одного треугольника равны соответственно двум сторонам и углу другого треугольника, то такие треугольники равны.

 

Если утверждений несколько, запишите их номера в порядке возрастания.

6. 

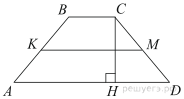
В трапеции АВСD боковые стороны AB и CD равны, СН — высота, проведённая к большему основанию AD. Найдите длину отрезка HD, если средняя линия KM трапеции равна 16, а меньшее основание BC равно 6.

7. 

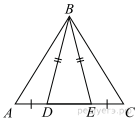На стороне АС треугольника АВС выбраны точки D и E так, что отрезки AD и CE равны (см. рисунок). Оказалось, что отрезки BD и BE тоже равны. Докажите, что треугольник АВС — равнобедренный.

8. 

Три окружности, радиусы которых равны 2, 3 и 10, попарно касаются внешним образом. Найдите радиус окружности, вписанной в треугольник, вершинами которого являются центры этих трёх окружностей.

Решения

Вариант1

1. 

На прямой AB взята точка M. Луч MD — биссектриса угла CMB. Известно, что ∠DMC = 41°. Найдите угол CMA. Ответ дайте в градусах.

Решение.

Поскольку MD — биссектриса, ∠DMB = ∠DMC = 41°. Углы CMA, DMC и DMB вместе составляют развёрнутый угол, откуда ∠CMA = 180° − ∠DMB − ∠DMC = 180° − 41° − 41° = 98°.

 

Ответ: 98.

2. 

Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Найдите угол ABC, если угол BAC равен 30°. Ответ дайте в градусах.

Решение.

Известно, что если центр описанной окружности лежит на стороне треугольника, то угол напротив этой стороны — прямой. Таким образом, угол   равен 90°. Таким образом:

 

 

Ответ: 60

3. 

В трапеции ABCD известно, что AD = 7, BC = 5, а её площадь равна 72. Найдите площадь трапеции BCNM, где MN – средняя линия трапеции ABCD.

Решение.

Проведём высоту   Средняя линия равна полусумме оснований:   Площадь трапеции равна произведению полусуммы оснований на высоту:

 

 

Поскольку   — средняя линия,   поэтому   Отрезки   и   равны,   по теореме Фалеса получаем, что   Найдём площадь трапеции 

 

 

Ответ: 33.

4. 

Найдите тангенс угла  , изображённого на рисунке.

Решение.

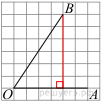Опустим перпендикуляр из точки B на прямую AO для получения прямоугольного треугольника. Тангенс угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему: 

 

Ответ: 1,5.

5. 

Какое из следующих утверждений верно?

1) Сумма углов выпуклого четырёхугольника равна 360 градусам.

2) Средняя линия трапеции равна сумме её оснований.

3) Любой параллелограмм можно вписать в окружность.

Решение.

Проверим каждое из утверждений.

1) «Сумма углов выпуклого четырёхугольника равна 360 градусам.» — верно, по теореме о сумме углов выпуклого многоугольника сумма углов n-угольника равна 180°(n − 2). Следовательно, сумма углов выпуклого четырёхугольника равна 360 градусам.

2) «Средняя линия трапеции равна сумме её оснований.» — неверно, Средняя линия трапеции равна полусумме её оснований.

3) «Любой параллелограмм можно вписать в окружность.» — неверно, в окружность можно вписать только четырёхугольник, сумма противоположенных углов которого равна 180°.

 

Ответ: 1.

6. 

Основания трапеции равны 16 и 34. Найдите отрезок, соединяющий середины диагоналей трапеции.

Решение.

Пусть в трапеции ABCD с основаниями BC = 16 и AD = 34. Обозначим середину диагонали AC через N, середину диагонали BD через M, а середину стороны CD через K.

Тогда NK — средняя линия треугольника ACD, MK — средняя линия треугольника BCD. Длина средней линии треугольника равна половине стороны, параллельной ей, то есть MK = BC/2 = 8, NK = AD/2 = 17. Значит, точки N, M и K лежат на одной прямой, и NM = NK − MK = 9.

 

Ответ: 9.

7. 

В остроугольном треугольнике ABC проведены высоты   и   Докажите, что углы   и   равны.

Решение.

Треугольники   и   имеют общую гипотенузу  . Поэтому точки   лежат на одной окружности. Углы   и   опираются на одну дугу, и поэтому равны.

8. 

Медиана BM треугольника ABC равна 3 и является диаметром окружности, пересекающей сторону BC в её середине. Найдите диаметр описанной окружности треугольника ABC.

Решение.

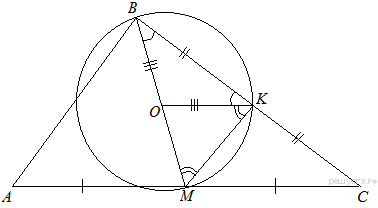Введём обозначения, как показано на рисунке. Рассмотрим треугольник   — он равнобедренный, следовательно,  . Аналогично в треугольнике   имеем:   Теперь рассмотрим треугольник  : сумма его углов равна 180°, поэтому

 

 

Поскольку кроме этого   имеем:

 

 

Рассмотрим треугольники   и   они прямоугольные, имеют общий катет и   равно   следовательно, эти треугольники равны, а значит,  .

Точка   отстоит на равное расстояние от всех трёх вершин треугольника,  , следовательно, точка   — центр окружности, описанной около треугольника  . Диаметр описанной окружности 

 

Ответ: 6.

Вариант2

1. 

В треугольнике   известно, что  ,   — биссектриса. Найдите угол  . Ответ дайте в градусах.

Решение.

Поскольку   — биссектриса,  .

Ответ: 24

2. 

В угол C величиной 57° вписана окружность, которая касается сторон угла в точках A и B, точка O - центр окружности. Найдите угол AOB. Ответ дайте в градусах.

Решение.

Радиус окружности перпендикулярен касательной в точке касания, поэтому углы CAO и OBC равны 90°. Сумма углов четырёхугольника равна 360°, откуда:

 

∠AOB = 360° −∠CAO − ∠OBC − ∠ACB = 360° − 90° − 90° − 57° = 123°.

Ответ: 123.

3. 

Найдите площадь трапеции, изображённой на рисунке.

Решение.

Площадь трапеции равна произведению полусуммы оснований на высоту:

 

 

Ответ: 42.

4.

Найдите тангенс угла  , изображённого на рисунке.

Решение.

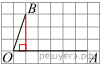Опустим перпендикуляр из точки B на прямую AO для получения прямоугольного треугольника. Тангенс угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему: 

 

Ответ: 3.

5. 

Какое из следующих утверждений верно?

 

1) Диагонали параллелограмма равны.

2) Площадь ромба равна произведению его стороны на высоту, проведённую к этой стороне.

3) Если две стороны и угол одного треугольника равны соответственно двум сторонам и углу другого треугольника, то такие треугольники равны.

 

Если утверждений несколько, запишите их номера в порядке возрастания.

Решение.

Проверим каждое из утверждений.

1) «Диагонали параллелограмма равны» — неверно, если в параллелограмме диагонали равны, то этот параллелограмм — прямоугольник, т. е. не у каждого параллелограмма диагонали равны.

2) «Площадь ромба равна произведению его стороны на высоту, проведённую к этой стороне.» — верно, ромб — частный случай параллелограмма, а площадь параллелограмма равна a · h.

3) «Если две стороны и угол одного треугольника равны соответственно двум сторонам и углу другого треугольника, то такие треугольники равны» — неверно, нет такого признака равенства треугольников.

 

Ответ: 2.

6. 

В трапеции АВСD боковые стороны AB и CD равны, СН — высота, проведённая к большему основанию AD. Найдите длину отрезка HD, если средняя линия KM трапеции равна 16, а меньшее основание BC равно 6.

Решение.

В трапеции средняя линия равна полусумме оснований, поэтому можем найти большее основание   зная   и 

 

 

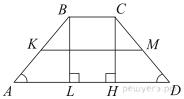
Проведём в трапеции вторую высоту   Трапеция равнобедренная, поэтому   Рассмотрим два треугольника:   и  , они прямоугольные, имеют равные углы и   равно   следовательно, эти треугольники равны. Таким образом, равны отрезки   и 

Также рассмотрим четырёхугольник  , все углы в нём — прямые, следовательно, это прямоугольник, значит, 

Теперь найдём длину отрезка 

 

 

Ответ: 10.

7. 

На стороне АС треугольника АВС выбраны точки D и E так, что отрезки AD и CE равны (см. рисунок). Оказалось, что отрезки BD и BE тоже равны. Докажите, что треугольник АВС — равнобедренный.

Решение.

Так как по условию   то треугольник   является равнобедренным. Пусть угол при основании этого треугольника равен x, тогда   Треугольники   и   равны по двум сторонам и углу между ними, поэтому   и треугольник   —равнобедренный.

8. 

Три окружности, радиусы которых равны 2, 3 и 10, попарно касаются внешним образом. Найдите радиус окружности, вписанной в треугольник, вершинами которого являются центры этих трёх окружностей.

Решение.

Стороны треугольника, вершинами которого является центры этих трёх окружностей, равны 5, 12 и 13. Поскольку   , этот треугольник прямоугольный. Площадь этого треугольника равна 30. В то же время, она равна произведению радиуса вписанной окружности на полупериметр. Значит, искомый радиус равен  .

Ответ: 2.

Контрольная работа №5

Тема: «Длина окружности и площадь круга».

Цель: проверить уровень усвоения ФГОС:

• знания и умения применять при решении задач формулы площадей круга и его частей, длин окружности и дуги;

• умение оформлять решение задачи.

I вариант.

Длина окружности равна 8π. Вычислить площадь круга, ограниченного данной окружностью. Градусная мера дуги окружности с радиусом 6см равна 300. Вычислите площадь кругового сектора, соответствующего этой дуге. Найдите длины дуг, на которые разбивают окружность два радиуса, если угол между

ними равен 720, а радиус окружности равен 6см. 4. Найдите длину окружности, если площадь вписанного в нее правильного шестиугольника равна 72 см2. 5.Найдите площадь фигуры, ограниченной дугой окружности и стягивающей ее хордой, если длина хорды равна 4см, а градусная мера дуги равна 600.

II вариант.

1. Площадь круга равна 324π. Вычислите длину окружности, ограничивающую данный круг.

1. Градусная мера дуги окружности с радиусом 4см равна 45⁰. Вычислите площадь кругового сектора, соответствующего этой дуге.

1. Найдите длины дуг, на которые разбивают окружность два радиуса, если угол между ними равен 36⁰, а радиус окружности равен 12см.

1. Найдите площадь круга, если площадь вписанного в ограничивающую его окружность квадрата равна 72 см².

1. Найдите площадь фигуры, ограниченной дугой окружности и стягивающей ее хордой, если длина хорды равна 2см, а диаметр окружности равен 4см.

Распределение заданий по содержанию и уровню сложности

Содержательная линия	Воспроиз- ведение знаний	Примене- ние знаний	Интеграция знаний	Процентное соотношение в тексте
Площадь круга и его частей. Длина дуги. Длина окружности.	№1,№2	№3, №4	№5	100%
Процентное соотношение заданий	40 %	40 %	20 %	100 %

Спецификация заданий и критерии оценивания

№ зада ния	Характеристика задания	Проверяемые элементы	Балл за выполнение проверяемо- го элемента	Балл за вы- полнение задания
1	Площадь круга. Длина окружности.	Знание формулы длины окружности.	1 балл	3 балла
		Знание формулы площади круга.	1 балл
		Вычисления.	1 балл
2	Площадь кругового сектора.	Знание формулы.	1 балл	3 балла
		Вычисления.	1 балл
		Оформление решения задачи.	1 балл
3	Длина дуги окружности.	Выполнение чертежа по условию задачи.	1 балл	4 балла
		Знание формулы.	1 балл
		Вычисления.	1 балл
		Оформление решения задачи.	1 балл
4	Площадь круга. Длина окружности.	Выполнение чертежа по условию задачи.	1 балл	6 баллов
		Знание формул площадей фигур.	1 балл
		Нахождение стороны правильного многоугольника.	1 балл
		Нахождение радиуса.	1 балл
		Вычисления длины окружности (площади круга).	1 балл
		Оформление решения задачи.	1 балл
5	Площадь сегмента.	Выполнение чертежа по условию задачи.	1 балл	5 баллов
		Нахождение радиуса окружности (угла дуги).	1 балл
		Нахождение площади сектора.	1 балл
		Нахождение площади треугольника.	1 балл
		Оформление решения задачи.	1 балл

Критерии оценивания:

1-10 баллов – «2»

11-14 баллов – «3» 15-19 балов – «4»

20-21 балл – «5»

СПЕЦИФИКАЦИЯ КОНТРОЛЬНЫХ ИЗМЕРИТЕЛЬНЫХ МАТЕРИАЛОВ

Диагностическая работа по курсу геометрии 9 класса.

1. Назначение диагностической работы - определитьуровень достижения учащимися предметных планируемых результатов по всем изученным темам за год, а также выявить уровень достижения метапредметных результатов. Каждое задание базового уровня в диагностической работе оценивает конкретный предметный планируемый результат, задания повышенного уровня сложности позволяют оценить и предметные, и метапредметные планируемые результаты.

Планируемые результаты: Проверить уровень достижения результатов по основным темам курса геометрии 9 класса для обеспечения возможности успешного продолжения образования на базовом уровне.

Критерии оценивания самостоятельной работы

Максимальный балл за выполнение работы составляет – 13 баллов. На основе баллов, выставленных за выполнение всех заданий работы, подсчитывается первичный балл, который переводится в отметку по пятибалльной шкале (таблица 1).

Таблица 1

Перевод баллов в отметку по пятибалльной шкале

Процент выполнения от максимального балла	Количество баллов	Цифровая отметка	Уровневая шкала
92-100	12-13	5	Повышенный
69-91	9-11	4
46-68	6-8	3	Базовый
Менее 46	Менее 6	2	Недостаточный

Продолжительность работы

Продолжительность диагностической работы 40 минут.

Распределение заданий по разделам программ(ы)

№ п/п	Раздел программы (содержательная линия)	Количество заданий базового уровня сложности	Количество заданий повышенного уровня сложности
1.	Геометрические фигуры	1
2.	Измерения и вычисления	3	2
3	Векторы и координаты на плоскости	3	1
	Всего	7	3

План диагностической работы

№ задания	Раздел программы (содержательная линия)		Проверяемый планируемый результат	Уровень сложности	Тип задания	Время выполнения(м ин)	Максимальный балл
1	Векторы и координаты на плоскости		оперировать на базовом уровне понятием вектор, длина вектора	Базовый	Со свободным, кратким однозначным ответом	3	1 балл
2	Измерения и вычисления. Средняя линия трапеции		оперировать на базовом уровне понятием подобие фигур	Базовый	Со свободным, кратким однозначным ответом	3	1 балл
3	Векторы и координаты Длина вектора		применять базовые тригонометрические соотношения для вычисления длин, в простейших случаях	Базовый	Со свободным, кратким однозначным ответом	3	1 балл
4	Векторы и координаты		оперировать на базовом уровне понятиями координаты на плоскости	Базовый	Со свободным, кратким однозначным ответом	3	1 балл
5	Измерения и вычисления Площадь		решать задачи на нахождение геометрических величин по образцам или алгоритмам.	Базовый	Со свободным, кратким однозначным ответом	3	1 балл
6	Измерения и вычисления. Длина окружности		решать задачи на нахождение геометрических величин по образцам или алгоритмам.	Базовый	Со свободным, кратким однозначным ответом	3	1 балл
7	Геометрические фигуры		оперировать на базовом уровне понятиями	Базовый	Со свободным, кратким однозначным ответом	3	1 балл
8	Измерения и вычисления.		применять геометрические факты	Повышенный	С развернутым ответом	6	2 балла
	Вписанная и описанная окружность		для решения задач, в том числе, предполагающих несколько шагов решения
9	Векторы и координаты		доказывать геометрические утверждения применять геометрические факты для решения задач, в том числе, предполагающих несколько шагов решения	Повышенный	С развернутым ответом	6	2 балла
10	Измерения вычисления. окружности	и Длина	доказывать геометрические утверждения применять геометрические факты для решения задач, в том числе, предполагающих несколько шагов решения	Повышенный	С развернутым ответом	7	2 балла
						40 мин	13 баллов

Инструкция по проверке и оценке работ

№ задания	Планируемый результат	Правильный ответ		Критерии оценивания / Максимальный балл
		Вариант1	Вариант2
1	Решение задачи на нахождение длины вектора, теорему Пифагора	4	13	1 балл
2	Решение задачи на свойство средней линии трапеции	23	6	1 балл
3	Решение задачи на нахождение длины вектора по координатам	5	13	1 балл

Диагностическая работа 9 класс

Фамилия____________________________ Имя__________________________ класс_______________

школа__________________________________________

ВариантI

1 часть

В каждом задании первой части необходимо записать верный ответ, в отведенном для этого месте. Каждый верный ответ оценивается в один балл.

1. В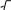 квадрате ABCD сторона равна 8 . Найдите длину вектора АС .

Ответ:______________________

1. Средняя линия трапеции равна 15, меньшее основание равно 7. Найдите большее основание.

Ответ:______________________

1. Найдите длину вектора АВ3;4

Ответ:______________________

1. Концы отрезка АВ имеют координаты А(7; 12), В(16; – 6 ) Найдите ординату точки С – середины этого отрезка.

Ответ: ___________________________

1. В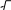 параллелограмме стороны равны 8 и 6 2 . Острый угол равен 45⁰. Найдите площадь параллелограмма.

Ответ: ___________________________

1. Длина окружности равна 18. Найдите радиус этой окружности.

Ответ: _______________________

7. Укажите номера верных утверждений.

1. Параллелограмм имеет две оси симметрии;

2. Любой треугольник имеет центр симметрии;

3. Каждый диаметр окружности является ее осью симметрии; 4) Правильный треугольник не имеет центра симметрии.

Ответ:______________________

II часть

Для записи решений и ответов каждого задания второй части используйте тетрадные листы в клетку. Запишите номер выполняемого задания, затем полное обоснованное решение и ответ. Каждое задание второй части оценивается от нуля до двух баллов.

1. Правильный четырехугольник с периметром, равным 16, вписан в окружность. Найдите площадь круга, ограниченного этой окружностью.

2. Дан треугольник АВС с координатами вершин: А (6; 8), В (4; 2), С (0; 6). Вычислите косинус угла С.

3. Самое удачное колесо обозрения для беглого знакомства с достопримечательностями Челябинска находится на берегу реки Миасс. С его высоты видно весь центр города — краеведческий музей, Кировку, набережную, Алое поле. Высота колеса обозрения 73 метра. За 11 минут кабина делает полный круг. Найдите скорость движения кабины колеса обозрения. Число 3. Ответ округлите до целых и выразите в км/ч.

Желаем успеха!