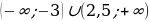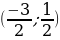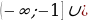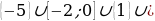План-конспект
фрагмента урока алгебры и начал математического анализа
в 10 классе по теме
"Решение неравенств методом интервалов"
Материал подготовила:
учитель математики
МБОУ «Николаевская школа»
Кузнецова Наталья Александровна
пгт Николаевка, 2019
Дата проведения: 14.10.2019
Цели урока:
Обобщить ранее изученный материал о решении неравенств методом интервалов
Закрепить умения и навыки в решении рациональных неравенств
Воспитывать познавательную активность, способствовать логическому мышлению, математической и общей грамотности
Выработать навыки самооценки своей работы.
Оборудование: раздаточный материал с критерием оценивания для самооценивания.
Структура урока
I. Организационный момент (1 мин)
II. Актуализация опорных знаний (3 мин)
III. Решение упражнений (фронтальная работа) (6 мин).
IV. Обобщение метода интервалов для неравенств высоких степеней (8 мин)
V. Подведение итогов урока (1 мин)
VI. Домашнее задание (1 мин)
Ход урока:
Организационный момент
Проверка готовности класса к уроку, приветствие, выявление отсутствующих. Сообщение темы урока, основных целей урока.
Актуализация опорных знаний (Повторение)
Вопрос: как решить неравенство методом интервалов?
Ответ: Алгоритм решения неравенств методом интервалов.
Пусть требуется решить неравенство 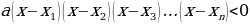 , где
, где 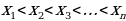
Найти корни уравнения 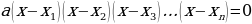
Отметить на числовой прямой корни 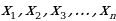
Определить знак выражения 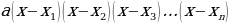 на каждом из получившихся промежутков
на каждом из получившихся промежутков
Записать ответ, выбрав промежутки с соответствующим знаку неравенства знаком.
Решить неравенство:
Пример 1.
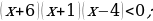
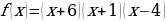 ;
;
Так как функция 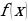 непрерывна в каждой точке своей области определения, то для решения данного неравенства можно использовать метод интервалов
непрерывна в каждой точке своей области определения, то для решения данного неравенства можно использовать метод интервалов
Нули функции 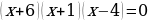 ;
;
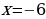 или
или 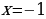 или
или 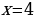






 - + - +
- + - +
-6 -1 4 x
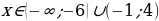
Ответ: 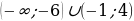 .
.
Пример 2.
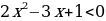 .
.
ОДЗ: 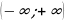
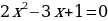 .
.
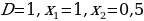
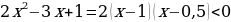




 + - +
+ - +
0,5 1 x
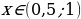
Ответ: 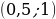 .
.
Пример 3.
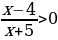
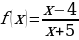
ОДЗ: 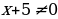

Нули функции
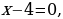
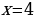 .
.




 + - +
+ - +
-5 4 x
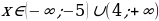
Ответ: 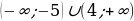 .
.
Фронтальная работа.
Вопрос: всегда ли чередуются знаки функции на промежутках? От чего это зависит?
Ответ: нет, не всегда. Это зависит от кратности корней, которые получаются в процессе решения неравенства.
Задание № 1.
Приведите пример неравенства, при решении которого можно встретить соседние интервалы с одинаковыми знаками.
Ответ: например, 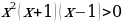
Нули функции
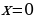 или
или 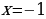 или
или 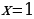




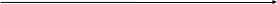


 + - - +
+ - - +
-1 0 1 x
Вопрос: что необходимо помнить при записи ответа после решения нестрогих неравенств?
Ответ: необходимо к найденным решениям строгого неравенства добавить корни функции.
Задание 2.
Установить соответствие при решении следующих неравенств:
А 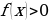
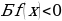
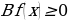
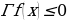
Если 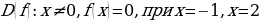 . Знаки функции определены на интервалах
. Знаки функции определены на интервалах




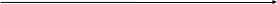


 - - + -
- - + -
-1 0 2 x
1) 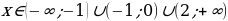
2) 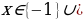
3) 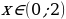
4) 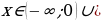
Ответ:
Самооценивание:
| Количество правильных ответов | отметка |
| 0-1 | 2 |
| 2 | 3 |
| 3 | 4 |
| 4 | 5 |
Практическое задание: решить неравенства методом интервалов с последующей взаимопроверкой и оцениванием
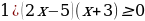 ,
,
2) 4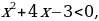
3) 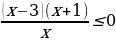 ,
,
4) 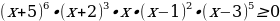 .
.
Ответы:
1) 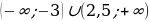
2) 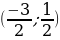
3) 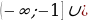
4) 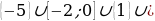
Критерий оценивания:
за каждый верно выполненный пример ставится 1 балл
| Количество правильных ответов | отметка |
| 0-1 | 2 |
| 2 | 3 |
| 3 | 4 |
| 4 | 5 |
Итоги урока, рефлексия
Понравился ли вам урок в целом?
Что особенно понравилось на уроке?
Научились ли вы решать неравенства методом интервалов?
Будете ли применять этот метод при решении заданий ЕГЭ?
Отметьте позицию на ступенях к совершенствованию знаний, на которой, на ваш взгляд, вы сейчас находитесь
В своих знаниях
В основном уверен!
Нужно еще уверен
Нуждаюсь повторить
в помощи
Домашнее задание:







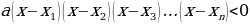 , где
, где 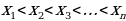
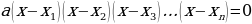
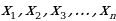
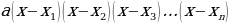 на каждом из получившихся промежутков
на каждом из получившихся промежутков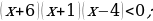
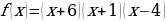 ;
;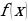 непрерывна в каждой точке своей области определения, то для решения данного неравенства можно использовать метод интервалов
непрерывна в каждой точке своей области определения, то для решения данного неравенства можно использовать метод интервалов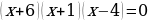 ;
;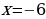 или
или 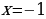 или
или 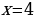


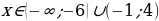
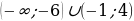 .
.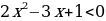 .
.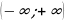
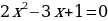 .
.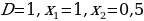
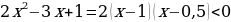
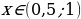
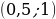 .
.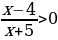
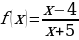
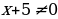

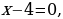
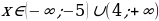
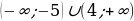 .
.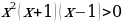
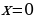 или
или 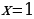
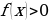
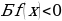
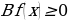
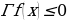
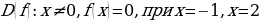 . Знаки функции определены на интервалах
. Знаки функции определены на интервалах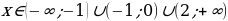
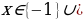
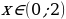
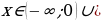
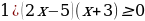 ,
,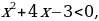
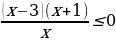 ,
,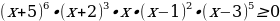 .
.