План-конспект урока математики в 10 классе
по теме «Обобщающее повторение тригонометрических функций и уравнений»
Эпиграф к уроку: «Кто смолоду делает и думает сам, тот становится потом надёжнее, крепче, умнее»
В. Шукшин.
Цели: повторить, обобщить и углубить приобретённые знания по тригонометрии; вызвать интерес к предмету; оказать помощь в подготовке к ЕГЭ по математике.
Тип урока: урок общеметодологической направленности
Оборудование: плакат, тест-карты, интерактивная доска, компьютер
Ход урока
Организационный момент
Актуализация знаний обучающихся. Разминка
Задание для разминки: найти ошибку в записях на доске
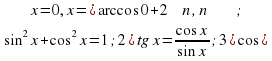
sin 2x = 2sin x cos x; 5) cos 2x = sin2 x
cos x; 5) cos 2x = sin2 x 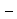 cos2 x; 6) tg x =
cos2 x; 6) tg x = 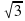 , x =
, x = 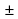 arctg
arctg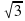
 .
.
Целеполагание и мотивация
Воспитательный момент о проверке каждого шага решения:
«Хотя доверчивости я пою хвалу, ну и проверка тоже не обуза…».
- Итак, послушайте стихотворение:
Хотя доверчивости я пою хвалу,
Ну и проверка тоже не обуза…
В определённом месте на углу
Встречались катет и гипотенуза.
У катета она была одна,
Гипотенузу он любил, не веря сплетням,
Но, в то же время, на углу соседнем
С другим встречалась катетом она.
И дело всё закончилось конфузом 
Вот после этого и верь гипотенузам.
(Во время чтения стихотворения на доске появляется чертёж прямоугольного треугольника ABC )
- Увы! Нельзя однозначно определить сложные взаимоотношения между людьми во взрослой жизни. А вот в прямоугольном треугольнике ABC определите,
а) Как называется отношение прилежащего катета к гипотенузе?
б) Как называется отношение прилежащего катета к противолежащему катету?
в) Как называется отношение противолежащего катета к гипотенузе?
г) Как называется отношение противолежащего катета к прилежащему?
- Сформулируйте, пожалуйста, тему и цели нашего урока
Обобщение и систематизация знаний
а) - Вспомним определение тригонометрических функций числового аргумента (Выступление ученика с заранее подготовленной информацией о тригонометрических функциях, включая, кроме основных, тригонометрические функции секанс x и косеканс x);
б) - «Счастливая случайность выпадает лишь на долю подготовленных умов», - говорил Луи Пастер.
- Итак, необходимо тренировать ум  и счастливый билет вам обеспечен.
и счастливый билет вам обеспечен.
Проведём тестирование «Преодоление полосы препятствий» по тест-картам. Выбирайте полосу препятствий согласно нумерации своей группы.
|  ctg x = 1 ctg x = 1
|
| 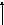
 tg x = tg x = 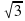
| 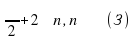

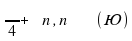
|
| 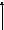 I группа I группа
 sin x = 1 sin x = 1
| 

|
| 
 cos x = 0 cos x = 0
| 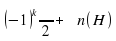
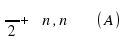
|
| 


|
|  ctg x = 0 ctg x = 0
|
| 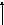
 tg x = tg x = 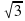
| 

|
| 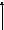 II группа II группа
 cos x = 1 cos x = 1
| 

|
| 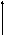
 sin x = 0 sin x = 0
| 

|
| 

|
|  cos x = cos x =
|
| 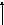
 ctg x = 0 ctg x = 0
|
|
| 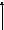 III группа III группа
 sin x = sin x = 
| 


|
| 
 tg x = 1 tg x = 1
| 

|
| 
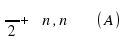
- Какие ключевые слова вы получили на финише? |
(ЗНАЮ, УМЕЮ, ПРАВ)
Применение знаний и умений в новой ситуации.
- Приступаем от простейших к более сложным тригонометрическим уравнениям. И познакомимся с ещё одним из способов решения тригонометрических уравнений.
- Тригонометрические уравнения можно решить способом сравнения аргументов одноимённых функций:
а)
б) ;
в) ;
г) .
1) Решим уравнение
Решение.
, откуда
.
 :
:
Решим уравнение  .
.
Решение.
 ,
,
, или
Ответ:  .
.
Контроль, анализ и коррекция
Решение.
,
,
Разделив обе части уравнения на  , придём к квадратному уравнению
, придём к квадратному уравнению
 , его корни tg x =
, его корни tg x = 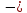 1 и tg x = 2 , отсюда
1 и tg x = 2 , отсюда
.
Ответ: наибольшим отрицательным корнем является  .
.
Дополнительный материал: решить уравнение и найти корни, принадлежащие  .
.
Рефлексия
- Каждое тригонометрическое уравнение – это загадка, и озарение по его решению приходит к тем, кто готов к нему, кто вооружён знанием формул, способов и методов решения, то есть «Счастливая случайность выпадает лишь на долю подготовленных умов»
Луи Пастер
- На каком качественном уровне вы подготовлены к решению тригонометрических уравнений? Можно проверить себя тестированием на сайтах по подготовке к ЕГЭ.
Подведение итогов.
- Что нового вы узнали на уроке?
- Достигнуты ли цели урока?
- Каким образом можно интерпретировать эпиграф, подобранный к нашему уроку?





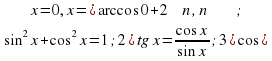
 cos x; 5) cos 2x = sin2 x
cos x; 5) cos 2x = sin2 x 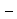 cos2 x; 6) tg x =
cos2 x; 6) tg x = 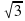 , x =
, x = 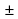 arctg
arctg .
.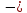 и счастливый билет вам обеспечен.
и счастливый билет вам обеспечен. ctg x = 1
ctg x = 1 
 tg x =
tg x = 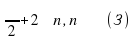

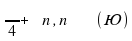
 I группа
I группа  sin x = 1
sin x = 1

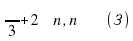
 cos x = 0
cos x = 0