Подготовка к ЕГЭ 2016. Задание №15.
Тема. Решение логарифмических неравенств, в которых основание входящего в него логарифма - функция.
1. Решение логарифмических неравенств
2. Решение логарифмических неравенств методом рационализации.
Повторить.


График.
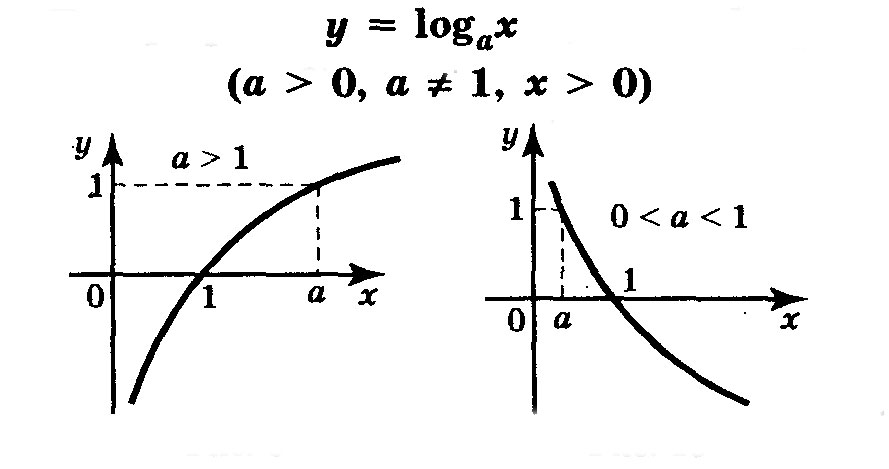
Определение возрастающей функции.
Функция y = f(x) возрастает на интервале X, если для любых a и b из интервала Х, таких что a b выполняется неравенство f(a) f(b). Другими словами – большему значению аргумента соответствует большее значение функции.
Определение убывающей функции.
Функция y = f(x) убывает на интервале X, если для любых a и b из интервала Х, таких что a b выполняется неравенство f(a) f(b). Другими словами – большему значению аргумента соответствует меньшее значение функции.
1. Решение логарифмических неравенств (основание логарифма - функция).
Часто, при решении логарифмических неравенств, встречаются задачи с переменным основанием логарифма, которые можно привести к виду, аналогичному неравенству.
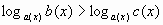 .
.
Это неравенство является стандартным школьным неравенством. Как правило, для его решения применяется переход к равносильной совокупности систем:
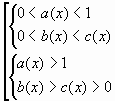
Недостатком данного метода является необходимость решения семи неравенств, не считая двух систем и одной совокупности
Рассмотрим пример решения логарифмического неравенства этим методом.
а) 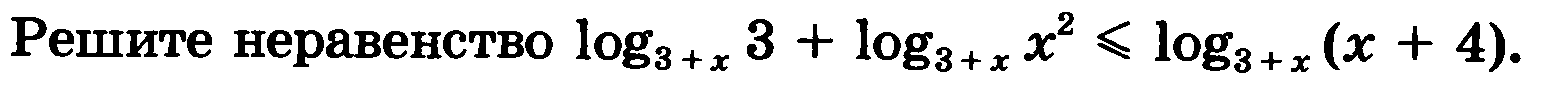
Решение.
1. log 3+x3+ log 3+x x2≤ log 3+x(x+4),
log 3+x 3x2≤ log 3+x(x+4),
| 1)При основании 3+х1, логарифмическая функция возрастающая. Поэтому получим систему:   3+х1 х-2 3+х1 х-2 3x2≤ x+4 ; 3x2- x-4≤0 Числа -1 и  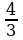 корни квадратного трёхчлена 3x2- x-4. Решением второго неравенства системы является отрезок [-1; корни квадратного трёхчлена 3x2- x-4. Решением второго неравенства системы является отрезок [-1; 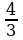 ], решением системы отрезок [-1; ], решением системы отрезок [-1; 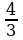 ] ] | 2)При основании 0 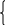 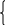 0 0 3x2 ≥ x+4 ; 3x2 –x-4≥0 Числа -1 и  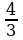 корни квадратного трёхчлена 3x2- x-4. Решением второго неравенства системы является ( -∞;-1] [ корни квадратного трёхчлена 3x2- x-4. Решением второго неравенства системы является ( -∞;-1] [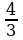 :∞), решением системы интервал (-3;-2); :∞), решением системы интервал (-3;-2); |
| Объединим решения: (-3;-2) [-1; 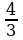 ] ] |
|
2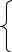 . Найдём ОДЗ. 3+х0 Первые два условия системы учтен в пункте 1. . Найдём ОДЗ. 3+х0 Первые два условия системы учтен в пункте 1. 3+х≠1 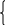 x20 x≠0 x20 x≠0 x+40, x-4. Итак ОДЗ:(-4;0)(0; ∞). |
3.Учитывая ОДЗ, найдём решение первоначального неравенства
(-3;-2) [-1;0)(0; 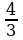 ]. Ответ: (-3;-2) [-1;0)(0;
]. Ответ: (-3;-2) [-1;0)(0; 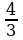 ]
]
Как выше было сказано, метод имеет свои недостатки. Рассмотрим метод решения неравенств такого типа другим методом, который называется «метод рационализации».
Вспомним, как в младших классах решали неравенства вида
(х-1)·(х-2)0. Их мы заменяли двумя системами:
х
 -10 х-1
-10 х-1
х-2 0 или х-2
Вспомним, как решали неравенство вида: log а(х)в(х)log а(х)с(х).
Их мы заменяли двумя системами:
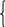
 а(х)1 0
а(х)1 0
а(х)в(х) или а(х)
Приведём системы к другому виду, не учитывая при этом условие 0, во второй системе.
а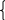
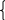 (х)-10 а(х)-1
(х)-10 а(х)-1
а(х)-в(х)0 или а(х)-в(х)
Получаем, что совокупность этих систем равносильна неравенству
(а(х)-1)( а(х)-в(х)0, а это неравенство равносильно неравенству
log а(х)в(х)log а(х)с(х) на ОДЗ данного уравнения. Равносильность останется верной для любого из знаков , Значит, логарифмические неравенство вида log а(х)в(х)log а(х)с(х) можно заменить рациональным неравенством вида (а(х)-1)( а(х)-в(х)0 . Этот метод называется методом рационализации.
2. Решение логарифмических неравенств вида log а(х)в(х)˅log а(х)с(х) методом рационализации.
1. Неравенство log а(х)в(х)˅log а(х)с(х) заменим неравенством (а(х)-1)( а(х)-в(х))0 и решаем его.
2. Находим ОДЗ неравенства log а(х)в(х)˅log а(х)с(х).
3. Находим пересечение множеств из пунктов 1 и 2. Это и есть решение неравенства log а(х)в(х)˅log а(х)с(х).
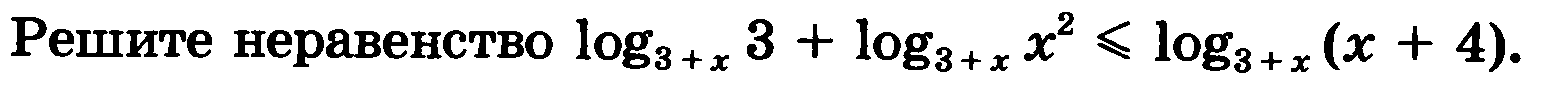 методом рационализации.
методом рационализации.
Решение.
1. Решим неравенство.
log 3+x3+ log 3+x x2≤ log 3+x(x+4)
log 3+x (3x2)≤ log 3+x(x+4)
(3+х-1)(3x2-(x+4)) ≤0
(х+2)(3x2-x-4) ≤0
(х+2)(х+1)(х-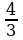 ) ≤,0, (Числа -1 и
) ≤,0, (Числа -1 и 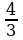 корни квадратного трёхчлена 3x2- x-4).
корни квадратного трёхчлена 3x2- x-4).
Методом интервалов определяем, что решением неравенства является
(-∞;-2) [-1;
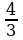 ]
]
| 2. Найдём ОДЗ |  3+х0 3+х0 3+х ≠1 x20 x+40 |  х-3 х-3 х ≠-2 x≠0 x-4 | 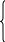 х-3 х-3 x≠0 х ≠-2 |
3. Учтём ОДЗ,(-3;-2) [-1;0)(0; 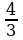 ]
]
Ответ: (-3;-2) [-1;0)(0; 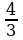 ]
]
Метод рационализации можно применить и к другим видам неравенств.
Заметим, таблица работает при условии f0, g0, h0, h≠1, р0, р≠1.
f, g –функции от х; h, p- числа или функции.
˅ — один из знаков ,
|
| Логарифмическое неравенство | Рациональное неравенство |
| 1 | log h f ˅log h g | (h-1)(f-g)˅0 |
| 2 | log h f ˅1 | (h-1)(f-h)˅0 |
| 3 | log h f ˅0 | (h-1)(f-1)˅0 |
| 4 | log h f ·log h g ˅0 | (h-1)(f-1) (p-1)(g-1)˅0 |
| 5 | log h f+ log h g ˅0 | (h-1)(fg-1)˅0 |
Главное в этой таблице – запомнить первую строку.
Заметим также, вторая и третья строчки таблицы — следствия первой. Во второй строке 1 представлена прежде как loghh , а в третьей — 0 представлен как logh1 .
Четвёртая и пятая строчки - еще парочка полезных следствий (надеюсь, вам несложно понять, откуда они вытекают).
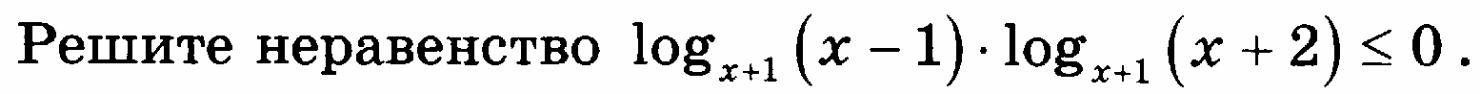
Для решения неравенства подходит переход из четвёртой строки.
| 4 | log h f ·log h g ˅0 | (h-1)(f-1) (p-1)(g-1)˅0 |
1. Решим неравенство, выполнив переход.
(х-1-1)(х+2-1)(х+1-1) (х+1-1)≤0
(х-2)(х+1)х2 ≤0.
(х-2)(х+1)х2=0,
х-2=0 или х+1=0 или х2=0
х1=2, х2=-1 х3,4=0

+
 - - +
- - +
-1 0 2
Решение неравенства без учёта ОДЗ: [-1,0)(0;2]
| 2. Найдём ОДЗ : |  х+10 х+10 х+1≠1 х-10 х+20, |  х -1 х -1 х≠0 х1 х-2, | х1.
|
3. Учтём ОДЗ: (1;2]
Ответ: (1;2]








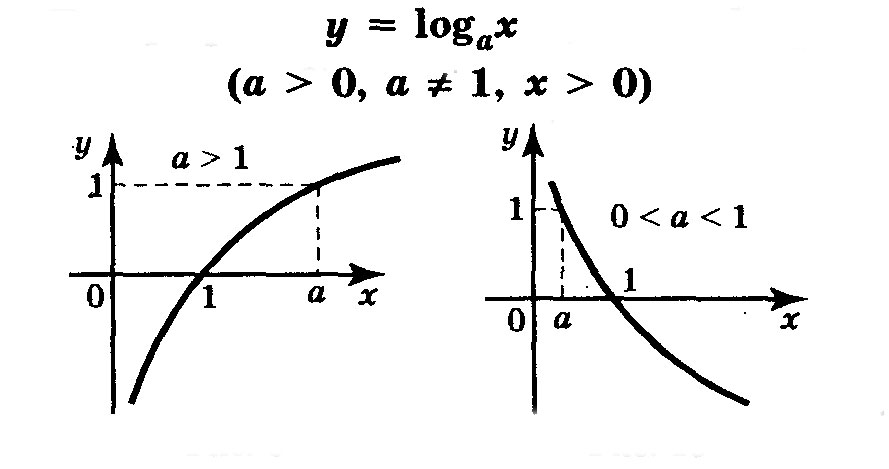
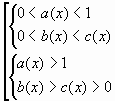
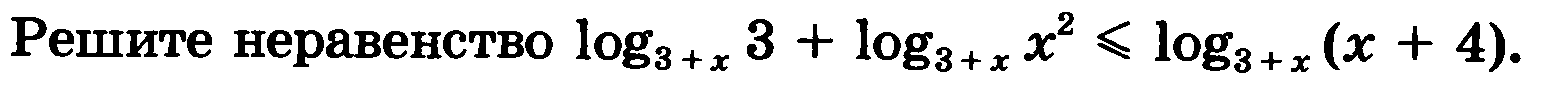

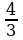 корни квадратного трёхчлена 3x2- x-4. Решением второго неравенства системы является отрезок [-1;
корни квадратного трёхчлена 3x2- x-4. Решением второго неравенства системы является отрезок [-1;  . Найдём ОДЗ. 3+х0 Первые два условия системы учтен в пункте 1.
. Найдём ОДЗ. 3+х0 Первые два условия системы учтен в пункте 1.
 -10 х-1
-10 х-1
 а(х)1 0
а(х)1 0
 3+х0
3+х0 х-3
х-3 х-3
х-3

 - - +
- - +









