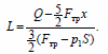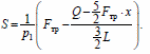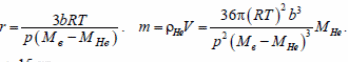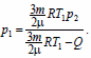Применение современных образовательных технологий при подготовки к ГИА по физике
Перед каждым учителем стоит вопрос, как организовать работу по подготовке к ГИА так, чтобы учащиеся показали хорошие знания.
Начинать подготовку к итоговой аттестации в 9 классе поздно. Поэтому вся работа учителя, начиная с 7 класса, должна быть направлена на развитие личностных качеств учащихся, обеспечивающих его развитие и саморазвитие. Организация различных форм и методов образовательной деятельности, направленных на развитие познавательных и коммуникативных потребностей и способностей учащихся, позволит сформировать личность с глубокой внутренней мотивацией и четко сформированными целями и направлениями дальнейшего саморазвития и самосовершенствования.
Сейчас знания физики востребованы как никогда. Это и развитие нанотехнологий, и создание высокоэкономичных энергосберегающих установок, и обеспечение современным оборудованием всех отраслей хозяйства. И в последние года всё большее и большее количество учащихся выбирают для итоговой аттестации физику.
Поэтому одна из проблем современного учителя физики является подготовка учащихся к ОГЭ и ЕГЭ. И в то же время сложность и объем заданий, включаемый в КИМы и особенно в ЕГЭ, чрезвычайно стали завышены по сравнению с заданиями, которые включались в выпускные экзамены ранее. Таким образом, ОГЭ и ЕГЭ по физике предъявляет большие требования к знаниям физического материала. Хорошие знания учащихся, их глубина и качество находятся в прямой зависимости от учебной деятельности ребят, как на уроке, так и во внеурочной деятельности. Внедрение на уроках физики современных технологий также является одним из условий качественного усвоения учебного материала. Какие же инновационные образовательные технологии и как могут помочь в организации работы по подготовки к ОГЭ и ЕГЭ?
В первую очередь, это личностно-ориентированное обучение. Подготовка к ОГЭ и ЕГЭ не даст высоких результатов, если готовиться к ним только 1 год или полгода. Поэтому я стараюсь, как можно раньше провести работу с детьми по определению места предмета физики в их дальнейшей жизни: нужно ли будет им сдавать предмет на выходе из школы или это для них обычный школьный предмет. С ребятами, которые определились в выборе физики, у меня складываются особые отношения. Я стараюсь держать связь с их родителями, чтобы не только дети, но и их родители знали о ходе подготовки, чаще всего эти ученики посещают элективные курсы, являются участниками различных конкурсов и олимпиад, потому что именно этот опыт на ОГЭ и ЕГЭ поможет решить сложные задачи из части С. Большое внимание я уделяю проведению индивидуальных консультаций с учащимися во внеурочное время. Во время подготовки к ОГЭ и ЕГЭ проходит систематическая тренировка по материалам ЕГЭ прошлых лет, неоднократное проведение в течение года «школьных ЕГЭ».
Полноценное изучение физики предполагает и включение компьютерных технологий в учебный процесс. Использование компьютера на уроках физики дает следующие положительные результаты: реализуется возможность учащихся перерабатывать громадный поток информации, который они получают, и стремление к самостоятельности; учащимся предоставляется возможность самостоятельной исследовательской работы с компьютерной моделью и индивидуальный темп обучения; у учителя высвобождается время на индивидуальную работу с учащимися (особенно с отстающими), в ходе которой он может корректировать процесс познания.
При подготовке к ЕГЭ по физике учащиеся используют интернет и образовательные обучающие программы сначала дома, а потом и на уроках повторения. В сети интернет имеется большое количество онлайн тестов с образовательных сайтов: www.fipi.ru;www.ege.edu.ru; www.obrnadzor.gov.ru; www.edu.ru; и другие. Ребята выполняют задания и сразу получают оценку «независимого лица».
Конечно, хороший результат дает самостоятельная работа учащихся по решению заданий из ОГЭ и ЕГЭ не только в школе, но и дома. Практика подготовки к ОГЭ и ЕГЭ в течение нескольких лет позволила мне накопить большой банк заданий в электронном виде, который я предлагаю выпускникам для домашней самостоятельной работы: здесь и варианты ОГЭ и ЕГЭ предыдущих лет, и решения задач уровня «С», и тематические тренажеры.
Большое внимание при обучении физике уделяю решению задач различного уровня и содержания с использованием мультимедийных презентаций. Использование современных мультимедийных пособий по физике позволило увидеть многие физические процессы, которые невозможно продемонстрировать в рамках обычной физической лаборатории на основе опытов. Такие сложные физические явления дети увидели в компьютерном исполнении. На уроках подготовки к экзаменам, широко используется мультимедийный материал, особенно подбор заданий тестового характера, количественные и качественные задачи.
Использование личностно-ориентированного обучения и компьютерных технологий при подготовке к ЕГЭ и ОГЭ позволяет эффективно решать проблему более полного погружения в специфику особенностей тестовых заданий ЕГЭ и ОГЭ, качественной подготовки учащихся.
Слово "технология" имеет греческие корни и в переводе означает применение научных и инженерных знаний, описывающее различные устройства, механизмы, способы, алгоритмы обработки информации для решения практических задач.
Информационные и коммуникационные технологии (ИКТ) – это новые педагогические технологии, которые позволяют не только модернизировать учебный процесс, повысить его эффективность, активизировать ученика, но и дифференцировать процесс с учётом индивидуальных особенностей каждого ученика, то есть создания и поддержки различных информационных ресурсов в компьютерной сети Интернет: сайтов, блогов, форумов, чатов и ICQ, электронных библиотек и энциклопедий передаваемые преподавателю через электронную почту или видеоконференции.
Одним из основных результатов обучения в сегодняшней школе становится информационно-коммуникативная компетентность, или грамотность,учащихся и учителей. Это понятие включает, прежде всего, умение учиться, искать и находить нужные сведения в огромных информационных массивах, в том числе в Интернете, структурировать и обрабатывать их в зависимости от конкретной задачи, выстраивать процесс собственного труда, уметь плодотворно работать в группе и творческом коллективе - участвовать в дискуссиях, уважать мнение оппонента, аргументированно отстаивать собственную точку зрения.
Современное мировоззрение невозможно без использования информационно-коммуникационных технологий, особенно это касается предметов естественно - научного цикла, т.к. именно они формируют единую картину мира и реализуют новые педагогические задачи, определяющие перспективу развития общего образования, что повышает эффективность обучения:
формирование индивидуальных образовательных траекторий школьников, подготовка обучаемых средствами информационных технологий к самостоятельной познавательной деятельности
конструирование обучаемыми собственных знаний, представлений о мире, умений, навыков и установок в ходе практической работы с объектами окружающего мира (включая компьютерные модели);
повышение качества и эффективности процесса обучения и контроля знаний учащихся, за счет реализации возможностей информационных технологий.
Обеспечение гибкости процесса обучения,
Организовать одновременно детей, обладающих различными способностями и возможностями.
ЕГЭ – важный шаг в жизни каждого выпускника, обдумывающего выбор своего будущего, стремящегося продолжить образование, овладеть профессиональными навыками для чего используются эффективные методы подготовки к итоговой аттестации, повышение сложности учебного материала, поддержка индивидуального развития ребенка. Наиболее удачным оказывается использование ИКТ, который работает на конкретного ребенка. Ученик берет столько, сколько может усвоить, работает в темпе и с теми нагрузками, которые оптимальны для него. Применяется в этой работе для групп разного уровня дидактические задания с инструктивным материалом из КИМов ЕГЭ прошлых лет:
уроки, включающих практические советы по выполнению заданий, интерактивные тренажеры,
интерактивных тестовых заданий, включенных в тренажеры и упражнения для контроля.
Для успешной сдачи ученик должен знать процедуру экзамена, понимать смысл предлагаемых заданий и владеть методами их выполнения, уметь правильно оформить результаты выполнения заданий, уметь распределять общее время экзамена на все задания, иметь собственную оценку своих достижений в изучении физики. В ходе такой работы формируются у учащихся навыки самообразования, самоорганизации и самоконтроля, которые необходимы для того, чтобы ученик был готов к полной самостоятельности в работе на экзамене.
Для высокого результата сдачи экзамена по ЕГЭ необходимо заниматься дополнительно индивидуально в удобные для себя дома часы. Выполнение тестовых заданий или в интернете on-line тестирование ЕГЭ или ГИА, позволяет моментально узнать свои результаты, выявить по заданиям уровня А, В, С и направить усилия каждого конкретного ученика на преодоление своих трудностей. Для учащихся это своеобразный тренинг, заставляющий поверить в свои силы, избавиться от страха. Особенно сложные темы могут разбираться в форме телеконференций и web-семинаров. Также учащиеся общаются за консультацией к учителю посредством электронной почты или форума.
Работая, таким образом, позволяет ученику не только углубить свои знания, но и получить навыки информационно-коммуникативной культуры работы в группах. В данных обстоятельствах возникла идея использования технологии скриншот в качестве решения при выполнения on-line тестирования - заданий по физике. Учащиеся, выполняя тестовые задания по интернету, сталкиваются с необходимостью сделать снимок того, что происходит на экране компьютера, проще говоря, сфотографировать экран или его часть, для того чтобы его переслать учителю. Такой снимок называется скриншот(от англ. слова screenshot снимок экрана) — изображение, полученное с экрана монитора активного окна или всей рабочей области экрана и т.д. путем нажатия на клавиатуре клавиш PrtScr (для всего экрана) или сочетания клавиш Alt + PrtScr (для текущего окна). Оно показывает в точности то, что видит пользователь на экране монитора или другого визуального устройства вывода: сообщения об ошибках, используемые программы и другую информацию. В буфере обмена операционной системы сохраняется снимок экрана. Затем полученный снимок может быть вставлен в графический редактор, обработан и сохранён. Таким образом его можно отправить в Твиттер, Фейсбук, ВКонтакт и использовать его как обычную картинку для вставки в Word, Photoshop или любое другое приложение.
Учащимся дается ссылка на задание и:
пройдя по этой ссылкам
выбрать ФИЗИКА
выполнить задание
нажмите кнопку ПРОВЕРИТЬ ЗАДАНИЕ.
снять скриншот выполненных заданий, которые отобразятся на экране.
выслать скриншот учителю через е-mail или через сообщение на личную страницу.
Ученик не обязан подстраиваться под определенный график, с другой стороны, четко сформулированный учебный план не дает расслабиться, заставляя придерживаться нужного темпа. К тому же сегодня, в эпоху сверхскоростных технологий и тотальной нехватки времени, общение через Internet зачастую оказывается эффективнее очного контакта. К примеру, преподаватель, получая вопросы по электронной почте, может ответить на них в удобное для себя время, не отвлекаясь от основного графика работы. Оперативная связь через интернет, индивидуальный подход дает возможность учителю организовать полноценное взаимодействие с учениками и сохранить результаты учебной деятельности каждого ребенка.
Выполнение тестовых заданий предполагают развитие способностей, как необходимость переделать огромное количество аналогичных заданий, параллельно повторяя весь школьный курс. Критерии оценки ЕГЭ не разделяют ошибки на «помарки», «описки», «огрехи невнимательности», не «щадят» потерю концентрации. Задания сформулированы на языке, не похожем на задания в учебниках, требуется точность и обоснованность ответов и т.д.
Образцы заданий № 30
Молекулярная физика
| Идеальный газ: |
силы молекулярного взаимодействия полностью отсутствуют; молекулы движутся направленно: одноатомные молекулы совершают только поступательное движение вдоль осей OX, OY, OZ; собственный объем молекул газа мал по сравнению с объемом газа; при соударении молекул между собой и со стенками сосуда они ведут себя как абсолютно упругие шарики конечных, но весьма малых размеров; в элементарном курсе физики рассматривают идеальные газы, молекулы которых состоят из одного атома |
| Газ: |
не имеет постоянной формы: занимает весь предоставленный ему объем; •обладает большим запасом внутренней энергии, поэтому может взрываться; имеет большие промежутки между молекулами = силы сцепления практически отсутствуют | Постоянная Авогадро | | 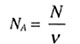
| | Количество вещества | | 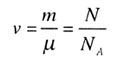
| | Молярная масса | | 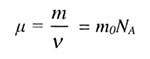
| | Постоянная Больцмана | | 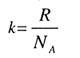
| | Масса одной молекулы | | 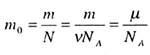
| | Основное уравнение МКТ | | 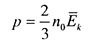
| | Концентрация молекул | | 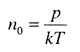
| | Средняя кинетическая энергия | | 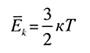
|
|
| Объединенный газовый закон |
| 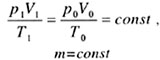 |
| Закон Бойля-Мариотта |
| p0V0 = p1V1 = const, T = const, m = const. |
| Закон Гей-Люссака |
| 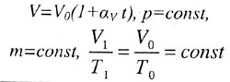 |
| Закон Шарля |
| 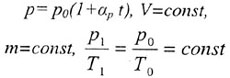 |
| Графики изобарного процесса представлены на рисунке 1 и называются изобарами: |
| 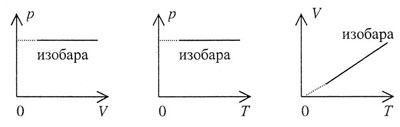 |
| Рис. 1 |
| Графики изотермического процесса представлены на рисунке 2 и называются изотермами: |
| 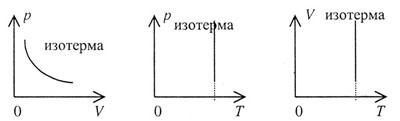 |
| Рис. 2 |
| Графики изохорного процесса представлены на рисунке 3 и называются изохорами: |
| 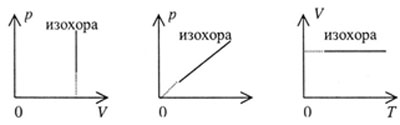 |
| Рис. 3 |
|
|
|
|
|
|
|
|
| Уравнение Менделеева-Клапейрона (уравнение состояния идеального газа) для произвольной массы газа с молярной массой 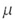 ): ): |
| 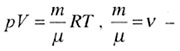 число молей число молей |
| Если v = 1 = уравнение состояния идеального газа для одного моля: |
| 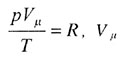 - молярный объем - молярный объем |
| Внутренняя энергия одного моля одноатомного идеального газа |
| 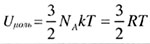 |
| Изменение внутренней энергии идеального одноатомного газа |
| 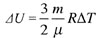 |
| |
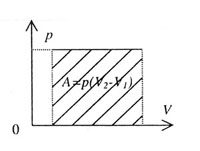
| Работа газа |
| A = p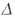 V V |
|
|
|
|
|
|
|
|
|
|
|
|
| 
|
| Работа А численно равна площади под графиком зависимости давления от объема. |
| Первый закон термодинамики |
| 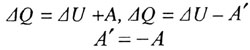 |
| А - работа, совершаемая системой над внешними телами; А' - работа совершаемая внешними телами над системой. |
| I закон термодинамики, адиабатный процесс |
| 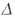 U = - A U = - A |
| Адиабатным называется процесс, происходящий без теплообмена с окружающей средой (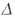 Q = 0). Q = 0). |
| I закон термодинамики, изохорный процесс |
| 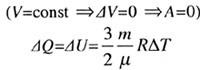 |
| I закон термодинамики, изотермический процесс |
| 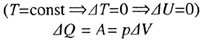 |
| I закон термодинамики, изобарный процесс |
| (p = const) |
| 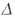 Q = Q = 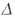 U + U + 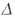 U + p U + p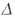 V V |
Задачи задание С3
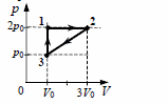
1.Один моль идеального одноатомного газа сначала нагрели, а затем охладили до первоначальной температуры 300 К, уменьшив давление в 3 раза (см. рисунок). Какое количество теплоты сообщено газу на участке 1 − 2?
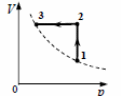
2. Один моль идеального одноатомного газа сначала нагрели, а затем охладили до первоначальной температуры 300 К, уменьшив давление в 3 раза (см. рисунок). Какое количество теплоты сообщено газу на участке 1 − 2?
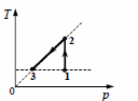
3. Один моль идеального одноатомного газа сначала охладили, а затем нагрели до первоначальной температуры 300 К, увеличив объем газа в 3 раза (см. рисунок). Какое количество теплоты отдал газ на участке 1 − 2?
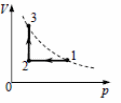
4. Один моль идеального одноатомного газа сначала охладили, а затем нагрели до первоначальной температуры 300 К, увеличив объем газа в 3 раза (см. рисунок). Какое количество теплоты отдал газ на участке 1 − 2?
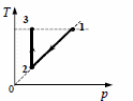
5. Одноатомный идеальный газ неизменной массы совершает циклический процесс, показанный на рисунке. За цикл от нагревателя газ получает количество теплоты Qн = 8 кДж. Чему равна работа газа за цикл?
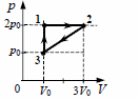
6. Одноатомный идеальный газ неизменной массы совершает циклический процесс, показанный на рисунке. Газ отдает за цикл холодильнику количество теплоты |Qх| = 8 кДж. Чему равна работа газа за цикл?
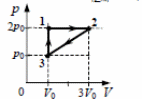
7. Одноатомный идеальный газ неизменной массы совершает циклический процесс, показанный на рисунке. За цикл газ совершает работу Aц = 5 кДж. Какое количество теплоты газ получает за цикл от нагревателя?
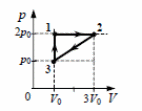
8. Одноатомный идеальный газ неизменной массы совершает циклический процесс, показанный на рисунке. За цикл газ совершает работу Aц = 5 кДж.Какое количество теплоты газ отдает за цикл холодильнику?
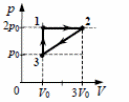
9. Один моль идеального одноатомного газа сначала изотермически расширился (Т1 = 300 К). Затем газ охладили, понизив давление в 3 раза (см. рисунок).Какое количество теплоты отдал газ на участке 2 − 3?
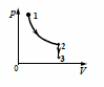
10. Один моль идеального одноатомного газа сначала изотермически расширился (Т1 = 300 К). Затем газ охладили, понизив давление в 3 раза (см. рисунок). Какое количество теплоты отдал газ на участке 2 − 3?
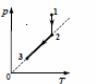
11. Идеальный одноатомный газ в количестве 1 моль сначала изотермически сжали (Т1 = 300 К).
Затем газ нагрели, повысив давление в 3 раза (см. рисунок). Какое количество теплоты получил
газ на участке 2 − 3?
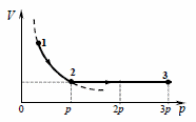
12. Идеальный одноатомный газ в количестве 1 моль сначала изотермически расширился (Т1 = 300 К). Затем газ изохорно нагрели, повысив давление в 3 раза (см. рисунок). Какое количество теплоты получил газ на участке 2 − 3?
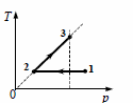
13. Идеальный одноатомный газ в количестве 1 моль сначала изотермически расширился
(Т1 = 300 К). Затем газ изохорно нагрели, повысив давление в 3 раза (см. рисунок). Какое количество теплоты получил газ на участке 2 − 3?
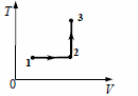
14. Постоянная масса одноатомного идеального газа совершает циклический процесс, показанный на рисунке. За цикл от нагревателя газ получает количество теплоты Qн = 8 кДж. Какую работу совершают внешние силы при переходе газа из состояния 2 в состояние 3?
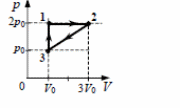
15. Постоянная масса одноатомного идеального газа совершает циклический процесс, показанный на рисунке. При переходе газа из состояния 2 в состояние 3 внешние силы совершают работу A23 = 5 кДж. Какое количество теплоты газ получает за цикл от нагревателя?
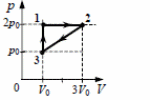
16. Постоянная масса одноатомного идеального газа совершает циклический процесс, показанный на рисунке. Газ отдает за цикл холодильнику количество теплоты |Qх| = 8 кДж. Какую работу совершают внешние силы при переходе газа из состояния 2 в состояние 3?
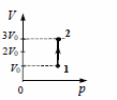
17. В сосуде с небольшой трещиной находится воздух, который может просачиваться сквозь трещину. Во время опыта давление воздуха в сосуде уменьшилось в 2 раза, а его абсолютная температура уменьшилась в 4 раза при неизменном объеме. Во сколько раз изменилась внутренняя энергия воздуха в сосуде? (Воздух считать идеальным газом.)
18. В сосуде под поршнем с небольшой трещиной находится газ. В опыте давление газа упало втрое, а его объем и температура уменьшились в 4 раза. Во сколько раз изменилась внутренняя энергия газа в сосуде? (Газ считать идеальным.)
19. На рисунке изображено изменение состояния 1 моль неона. Начальная температура газа 0°С. Какое количество теплоты сообщено газу в этом процессе?
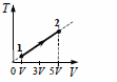
20. На рисунке изображено изменение состояния 1 моль неона. Начальная температура газа 27°С. Какое количество теплоты сообщено газу в этом процессе?
21. В горизонтальном цилиндрическом сосуде, закрытом поршнем, находится одноатомный идеальный газ. Первоначальное давление газа p1 = 4·105 Па. Расстояние от дна сосуда до поршня L = 30 см. Площадь поперечного сечения поршня S = 25 см2. В результате медленного нагревания газа поршень сдвинулся на расстояние x = 10 см. При движении поршня на него со стороны стенок сосуда действует сила трения величиной Fтр = 3·103 Н. Какое количество теплоты получил газ в этом процессе? Считать, что сосуд находится в вакууме.
22. В горизонтальном цилиндрическом сосуде, закрытом поршнем, находится одноатомный идеальный газ. Первоначальное давление газа p1 = 4·105 Па. Расстояние от дна сосуда до поршня равно L. Площадь поперечного сечения поршня S = 25 см2. В результате медленного нагревания газ получил количество теплоты Q = 1,65 кДж, а поршень сдвинулся на расстояние x = 10 см. При движении поршня на него со стороны стенок сосуда действует сила трения величиной Fтр = 3·103 Н. Найдите L. Считать, что сосуд находится в вакууме.
23. В горизонтальном цилиндрическом сосуде, закрытом поршнем, находится одноатомный идеальный газ. Первоначальное давление газа p1 = 4·105 Па. Расстояние от дна сосуда до поршня L = 30 см. Площадь поперечного сечения поршня S = 25 см2. В результате медленного нагревания газ получил количество теплоты Q = 1,65 кДж, а поршень сдвинулся на расстояние x. При движении поршня на него со стороны стенок сосуда действует сила трения величиной Fтр = 3·103 Н. Найдите x. Считать, что сосуд находится в вакууме.
24. В горизонтальном цилиндрическом сосуде, закрытом поршнем, находится одноатомный идеальный газ. Первоначальное давление газа p1 = 4·105 Па. Расстояние от дна сосуда до поршня L = 30 см. Площадь поперечного сечения поршня равна S. В результате медленного нагревания газ получил количество теплоты Q = 1,65 кДж. При этом поршень некоторое время покоился, а потом медленно сдвинулся на расстояние x = 10 см. При движении поршня на него со стороны стенок сосуда действует сила трения величиной Fтр = 3·103 Н. Найдите S. Считать, что сосуд находится в вакууме.
25. Сферическую оболочку воздушного шара делают из материала, квадратный метр которого имеет массу 1 кг. Радиус оболочки шара r = 2,7 м.Шар наполняют газом при атмосферном давлении 105 Па. Температура газа и окружающего воздуха одинакова и равна 0оС. Определите молярную массу газа, если оказалось, что шар может в таких условиях поднять только себя. (Площадь сферы S = 4πr2, объем шара V = 4/3 πr3.)
26. Сферическую оболочку воздушного шара делают из материала, квадратный метр которого имеет массу 1 кг. Шар наполняют гелием при атмосферном давлении 105 Па. Определите минимальную массу оболочки, при которой шар начнет поднимать сам себя. Температура гелия и окружаю-
щего воздуха одинакова и равна 0оС. (Площадь сферы S = 4πr2, объем шара V = 4/3 πr3.)
27. Сферическая оболочка воздушного шара сделана из материала, квадратный метр которого имеет массу 1 кг. Шар наполнен газом при атмосферном давлении 105 Па. Во сколько раз молярная масса воздуха больше молярной массы газа, которым наполнен шар, если шар поднимает сам себя
при радиусе 2,7 м? Температура газа и окружающего воздуха одинакова и равна 0оС. (Площадь сферы S = 4πr2, объем шара V = 4/3 πr3.)
28. Сферическая оболочка воздушного шара сделана из материала, квадратный метр которого имеет массу 1 кг. Шар наполнен гелием при атмосферном давлении 105 Па. Определите массу гелия, при которой шар поднимает сам себя. Температура гелия и окружающего воздуха одинакова и
равна 0оС. (Площадь сферы S = 4πr2, объем шара V = 4/3 πr3.)
29. В закрытом сосуде находится одноатомный идеальный газ, масса которого 12 г. Вначале давление в сосуде было равно 4·105 Па при температуре 400 К. После охлаждения газа давление понизилось до 2·105 Па. Какова молярная масса газа, если отданное им количество теплоты равно 7,5 кДж?
30. В закрытом сосуде находится одноатомный идеальный газ, масса которого 12 г, а молярная масса 0,004 кг/моль. Вначале температура газа была равна 400 К. В результате охлаждения газа давление в сосуде понизилось до 2·105 Па. Каким было давление в сосуде до охлаждения, если отданное
газом количество теплоты 7,5 кДж?
31. В горизонтальном цилиндрическом сосуде, закрытом поршнем, находится одноатомный идеальный газ. Площадь поперечного сечения поршня S = 30 см2. Давление окружающего воздуха p = 105 Па. Трение между поршнем и стенками сосуда пренебрежимо мало. Какое количество теплоты нужно отвести от газа при его медленном охлаждении, чтобы поршень передвинулся на расстояние x = 10 см?
32. В горизонтальном цилиндрическом сосуде, закрытом поршнем, находится одноатомный идеальный газ. Площадь поперечного сечения поршня S = 30 см2. Давление окружающего воздуха p = 105 Па. Трение между поршнем и стенками сосуда пренебрежимо мало. В процессе медленного
охлаждения от газа отведено количество теплоты |Q| = 75 Дж. На какое расстояние передвинулся при этом поршень?
33. В горизонтальном цилиндрическом сосуде, закрытом поршнем, находится одноатомный идеальный газ. Давление окружающего воздуха p = 105 Па. Трение между поршнем и стенками сосуда пренебрежимо мало. В процессе медленного охлаждения от газа отведено количество теп-
лоты |Q| = 75 Дж. При этом поршень передвинулся на расстояние x = 10 см. Чему равна площадь поперечного сечения поршня?
34. В горизонтальном цилиндрическом сосуде, закрытом поршнем, находится одноатомный идеальный газ. Площадь поперечного сечения поршня S = 25 см2. Трение между поршнем и стенками сосуда пренебрежимо мало. В процессе медленного охлаждения от газа отведено количество теплоты |Q| = 75 Дж. При этом поршень передвинулся на расстояние x = 10 см. Чему равно давление окружающего воздуха?
35. Некоторое количество одноатомного идеального газа расширяется из одного и того же начального состояния (р1, V1) до одного и того же конечного объема V2 первый раз по изобаре, а второй — по адиабате (см. рисунок). Отношение работы газа на изобаре А12 к работе газа на адиабате А13 равно 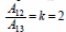
Чему равно отношение х количества теплоты Q12, полученного газом на изобаре от нагревателя, к модулю изменения внутренней энергии газа| U3 −U1| на адиабате?
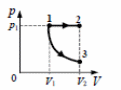
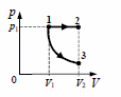
36. Некоторое количество одноатомного идеального газа расширяется из одного и того же начального состояния (р1, V1) до одного и того же конечного объема V2 первый раз по изобаре, а второй — по адиабате (см.рисунок). Отношение количества теплоты Q12, полученного газом на изобаре от нагревателя, к модулю изменения внутренней энергии газа |U3 −U1| на адиабате 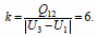 Чему равно отношение х работы газа на изобаре А12 к работе газа на адиабате А13 ?
Чему равно отношение х работы газа на изобаре А12 к работе газа на адиабате А13 ?
Решения
1.Согласно первому закону термодинамики, Q12 = ΔU12 + A12, где ΔU12 = 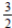 νR(Т2 − Т1);
νR(Т2 − Т1);
A12 = νR(Т2 − Т1).
Следовательно, Q12 = 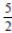 νR(Т2 − Т1).
νR(Т2 − Т1).
Согласно закону Шарля, 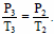
Cледовательно, Т2 = 3Т1 и Q12 = 5νRТ1. Ответ: Q12 ≈ 12,5 кДж.
2. Согласно первому закону термодинамики, Q12 = ΔU12 + A12, где ΔU12 = 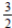 νR(Т2 − Т1);
νR(Т2 − Т1);
A12 = νR(Т2 − Т1).
Следовательно, Q12 = 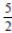 νR(Т2 − Т1).
νR(Т2 − Т1).
Согласно закону Шарля, 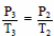
Cледовательно, Т2 = 3Т1 и Q12 = 5νRТ1. Ответ: Q12 ≈ 12,5 кДж
3. Согласно первому закону термодинамики, ΔU = Q + A.На участке 1 – 2 имеем: А12 = 0. Следовательно, Q12 = ΔU12.
Но 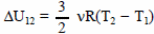
Согласно закону Гей-Люссака, 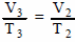
Следовательно, 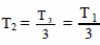
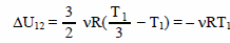
|Q12|= νRТ1 ≈ 2,5 (кДж). Ответ: Q12 ≈ 2,5 кДж.
4. Согласно первому закону термодинамики, ΔU = Q + A.
На участке 1 – 2 имеем: А12 = 0. Следовательно, Q12 = ΔU12.
Но 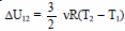
Согласно закону Гей-Люссака, 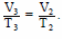
Следовательно, 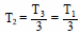 ,
, 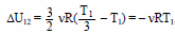
|Q12| = νRТ1 ≈ 2,5 (кДж). Ответ: Q12 ≈ 2,5 кДж
5. За цикл количество теплоты, полученное от нагревателя:
Qн = Q12 + Q31 = (U2 – U3) + A12 = (3/2)(νRT2 – νRT3) + 2p0 2V0 =
= (3/2)(2p0 3V0 – p0V0) + 4p0V0 = (23/2)p0V0.
Работа газа за цикл Aц = (p0/2) 2V0 = p0V0.
Отсюда Ац = (2/23) Qн ≈ 700 Дж. Ответ: Ац ≈ 700 Дж.
6. За цикл количество теплоты, отданное холодильнику:
|Qх| = (U2 – U3) + |A23| = (3/2)(νRT2 – νRT3) + (1/2)(p0 + 2p0) 2V0 == (3/2)(2p0 3V0 – p0V0) + 3p0V0 = =(21/2)p0V0.
Работа газа за цикл Aц = (p0/2) 2V0 = p0V0.
Отсюда Ац = (2/21) |Qх| ≈ 760 Дж. Ответ: Ац ≈ 760 Дж.
7. За цикл количество теплоты, полученное от нагревателя:
Qн = Q12 + Q31 = (U2 – U3) + A12 = (3/2)(νRT2 – νRT3) + 2p0 2V0 == (3/2)(2p0 3V0 – p0V0) + +4p0V0 = =(23/2)p0V0.
Работа газа за цикл Aц = (p0/2) 2V0 = p0V0.
Отсюда Qн = (23/2) Aц = 57,5 кДж. Ответ: Qн = 57,5 кДж.
8. За цикл количество теплоты, отданное холодильнику:
|Qх| = (U2 – U3) + |A23| = (3/2)(νRT2 – νRT3) + (1/2)(p0 + 2p0) 2V0 == (3/2)(2p0 3V0 – p0V0) + +3p0V0 = =(21/2)p0V0.
Работа газа за цикл Aц = (p0/2) 2V0 = p0V0.
Отсюда |Qх| = (21/2)Ац = 52,5 (кДж). Ответ: |Qх| = 52,5 (кДж).
9. Согласно первому закону термодинамики, ΔU = Q + A.
На участке 1 – 2 имеем: А12 = 0. Следовательно, Q12 = ΔU12.
Но 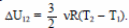
Согласно закону Гей-Люссака, 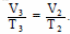
Следовательно, 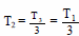 ,
, 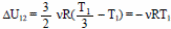
|Q12|= νRТ1 ≈ 2,5 (кДж). Ответ: Q12 ≈ 2,5 кДж.
10. Согласно первому закону термодинамики, ΔU = Q + A.
На участке 1 – 2 имеем: А12 = 0. Следовательно, Q12 = ΔU12.
Но 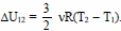
Согласно закону Гей-Люссака, 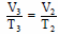
Следовательно, 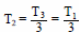
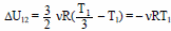
|Q12| = νRТ1 ≈ 2,5 (кДж). Ответ: Q12 ≈ 2,5 кДж.
11. Запишем I закон термодинамики Q = ΔU + A для изохорного нагревания
2–3: Q23 = ΔU23, так как А23 = 0.
Поскольку 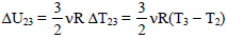 ,то
,то 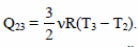
Закон Шарля или уравнение Клапейрона-Менделеева для состояний 2 и 3:
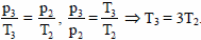
Так как по условию 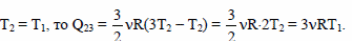
Q23 = 3·1·8,31·300 = 7479(Дж). Ответ: Q23 ≈ 7,5 кДж.
12. Запишем I закон термодинамики Q = ΔU + A для изохорного нагревания
2–3: Q23 = ΔU23, учитывая, что А23 = 0 .
Поскольку 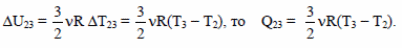
Закон Шарля для состояний 2 и 3: 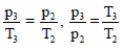 откуда Т3 = 3Т2.
откуда Т3 = 3Т2.
Так как по условию Т2 = Т1, то 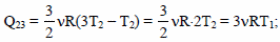
Q23 = 3·1·8,31·300 = 7479(Дж). Ответ: Q23 ≈ 7,5 кДж
13. Запишем I закон термодинамики Q = ΔU + A для изохорного нагревания
2–3, учитывая, что Δ А23 = 0, Q23 = ΔU23.
Поскольку 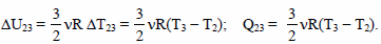
Закон Шарля для состояний 2 и 3: 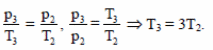
Так как по условию Т2 = Т1, то 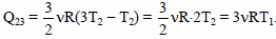
Q23 = 3·1·8,31·300 = 7479(Дж). Ответ: Q23 ≈ 7,5 кДж
14. Из анализа графика цикла работа газа при переходе из 1 в 2:
A12 = 2p0·2V0 = 4p0V0.
Количество теплоты, полученное за цикл от нагревателя:
Qн = Q12 + Q31 = (U2 – U3) + A12 = (3/2)(νRT2 – νRT3) + 4p0V0 = (3/2)(2p0·3V0 – p0V0) + 4p0V0= =(23/2)p0V0.
Работа внешних сил над газом при переходе из 2 в 3:
A23 внешн = 0,5(p0 + 2p0)·2V0 = 3p0V0 = (6/23)Qн.
Ответ: A23 внешн ≈ 2,1 кДж.
15. Из анализа графика цикла работа внешних сил над газом при переходе 2–3:
A23 = 0,5(p0 + 2p0)·2V0 = 3p0V0.
Работа газа при переходе из 1 в 2: A12 = 2p0·2V0 = 4p0V0.
Количество теплоты, полученное за цикл от нагревателя:
Qн = Q12 + Q31 = (U2 – U3) + A12 = (3/2)(νRT2 – νRT3) + 4p0V0 = (3/2)(2p0·3V0 – p0V0) + 4p0V0= =(23/2)p0V0.
Qн = (23/6)A23. Ответ: Qн ≈ 19 кДж.
16. Из анализа графика цикла работа внешних сил над газом при переходе из
2 в 3: A23 внешн = 0,5(p0 + 2p0)·2V0 = 3p0V0 = (2/7)|Qх|.
Количество теплоты, переданное за цикл холодильнику:
|Qх| = |Q23| = (U2 – U3) + A32 = (3/2)(νRT2 – νRT3) + 3p0V0 = (3/2)(2p0·3V0 – p0V0) + 3p0V0 = =(21/2)p0V0.
Ответ: A23 внешн ≈ 2,3 кДж.
17. Внутренняя энергия идеального газа U = N · E0 , где E0 – средняя энергия одной молекулы газа, а N – их число в сосуде. E0 ~kT , а N = ν· N A.
Отсюда U ~ν· N A · kT = νRT .
При этом pV = νRT . Следовательно, U ~ pV. Поскольку объем не изменился, а давление в два раза уменьшилось, то произведение pV уменьшилось в два раза.
Ответ: внутренняя энергия газа в сосуде уменьшилась в два раза.
18. Внутренняя энергия идеального газа U = N · E0 , где E0 – средняя энергия одной молекулы газа, а N – их число в сосуде. E0 ~kT , а N = ν· N A.
Отсюда U ~ν· N A · kT = νRT .
При этом pV = νRT . Следовательно, U ~ pV. Поскольку объем уменьшился в четыре раза, а давление уменьшилось в три раза, то произведение pV уменьшилось в двенадцать раз.
Ответ: внутренняя энергия газа в сосуде уменьшилась в 12 раз.
19. В состоянии 1: pV = RT1, в состоянии 2: p·5V = RT2. Отсюда Т2 = 5 Т1.
Количество теплоты, получаемое системой в изобарном процессе,
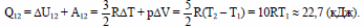
Ответ: Q12 ≈ 22,7 кДж.
20. В состоянии 1: pV0 = RT1, в состоянии 2: p·3V0 = RT2. Отсюда Т2 = 3 Т1.
Количество теплоты, получаемое системой в изобарном процессе,
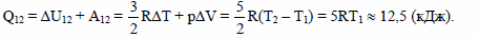
Ответ: Q12 ≈ 12,5 кДж
21.
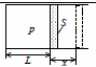 1) Поршень будет медленно двигаться, если сила давления газа на поршень и сила трения со стороны стенок сосуда уравновесят друг друга: p2S =Fтр , откуда
1) Поршень будет медленно двигаться, если сила давления газа на поршень и сила трения со стороны стенок сосуда уравновесят друг друга: p2S =Fтр , откуда 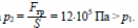
2) Поэтому при нагревании газа поршень будет неподвижен, пока давление газа не достигнет значения р2. В этом процессе газ получает количество теплоты Q12.
Затем поршень будет сдвигаться, увеличивая объем газа, при постоянном давлении. В этом процессе газ получает количество теплоты Q23.
3) В процессе нагревания, в соответствии с первым началом термодинамики, газ получит количество теплоты:
Q = Q12 +Q23 = (U3 −U1) + p2Sx = (U3 −U1) + Fтрx.
4) Внутренняя энергия одноатомного идеального газа: 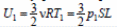 в начальном состоянии,
в начальном состоянии,
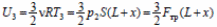 в конечном состоянии.
в конечном состоянии.
5) Из пп. 3, 4 получаем 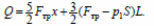
Ответ: Q = 1,65 кДж
22.
 1) Поршень будет медленно двигаться, если сила давления газа на поршень и сила трения со стороны стенок сосуда уравновесят друг друга: p2S = Fтр ,откуда
1) Поршень будет медленно двигаться, если сила давления газа на поршень и сила трения со стороны стенок сосуда уравновесят друг друга: p2S = Fтр ,откуда 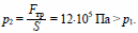
2) Поэтому при нагревании газа поршень будет неподвижен, пока давление газа не достигнет значения р2. В этом процессе газ получает количество теплоты Q12. Затем поршень будет сдвигаться, увеличивая объем газа, при постоянном давлении. В этом процессе газ получает количество теплоты Q23.
3) В процессе нагревания, в соответствии с первым началом термодинамики, газ получит количество теплоты: Q = Q12 +Q23 = (U3 −U1) + p2Sx = (U3 −U1) + Fтрx.
4) Внутренняя энергия одноатомного идеального газа: 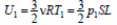 в начальном состоянии,
в начальном состоянии,
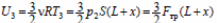 в конечном состоянии.
в конечном состоянии.
5) Из пп. 3, 4 получаем
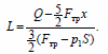
Ответ: L = 0,3 м.
23.
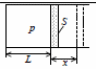
Поршень будет медленно двигаться, если сила давления газа на поршень и сила трения со стороны стенок сосуда уравновесят друг друга: p2S = Fтр , откуда 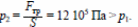
2) Поэтому при нагревании газа поршень будет неподвижен, пока давление газа не достигнет значения р2. В этом процессе газ получает количество теплоты Q12.Затем поршень будет сдвигаться, увеличивая объем газа, при постоянном давлении. В этом процессе газ получает количество теплоты Q23.
3) В процессе нагревания, в соответствии с первым началом термодинамики, газ получит количество теплоты: Q = Q12 +Q23 = (U3 −U1) + p2Sx = (U3 −U1) + Fтрx.
4) Внутренняя энергия одноатомного идеального газа:
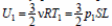 в начальном состоянии,
в начальном состоянии, 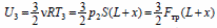 в конечном состоянии.
в конечном состоянии.
5) Из пп. 3, 4 получаем
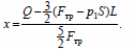
Ответ: x = 0,1 м.
24.

1. Поршень будет медленно двигаться, если сила давления газа на поршень и сила трения со стороны стенок сосуда уравновесят друг друга: p2S = Fтр , откуда 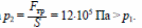
2) Поэтому при нагревании газа поршень будет неподвижен, пока давление газа не достигнет значения р2. В этом процессе газ получает количество теплоты Q12. Затем поршень будет сдвигаться, увеличивая объем газа, при постоянном давлении. В этом процессе газ получает количество теплоты Q23.
3) В процессе нагревания, в соответствии с первым началом термодинамики, газ получит количество теплоты:
Q = Q12 +Q23 = (U3 −U1) + p2Sx = (U3 −U1) + Fтрx.
4) Внутренняя энергия одноатомного идеального газа: 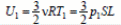 – в начальном состоянии,
– в начальном состоянии, 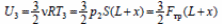 – в конечном состоянии.
– в конечном состоянии.
5) Из пп. 3, 4 получаем
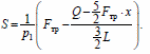
Ответ: S = 25 см2.
25. II закон Ньютона в проекциях на вертикаль: FA = mгазаg + mобg .
Силы выражены через радиус r:
ρвgV = moбg + mгазаg = bSg + ρгазаVg → ρ g 4/3 πr3 = b4 πr2 g + ρ g 4/3 πr3 и радиус: 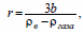
где b – отношение массы оболочки к ее площади.
Плотности газа и воздуха: 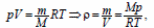
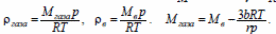
Ответ: Mгаза ≈ 4·10−3 кг/моль.
26. II закон Ньютона в проекциях на вертикаль: FA = mHeg + mобg .
Силы выражены через радиус r:
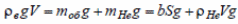
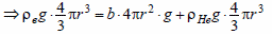 и радиус:
и радиус: 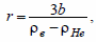
где b – отношение массы оболочки к ее площади.
Плотности гелия и воздуха: 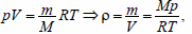
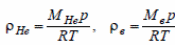
Радиус: 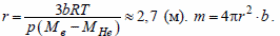
Ответ: m ≈ 92 кг.
27. II закон Ньютона в проекциях на вертикаль: FA = mгg + mобg .
Силы выражены через радиус r:
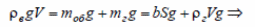
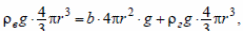 найдем радиус:
найдем радиус: 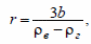
где b –отношение массы оболочки к ее площади.
Плотности гелия и воздуха: 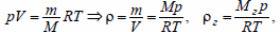
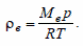
Молярные массы 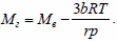
Ответ: 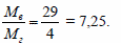
28. II закон Ньютона в проекциях на вертикаль: FA = mHeg + mобg .
Силы выражены через радиус r:
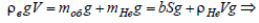
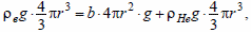 радиус:
радиус: 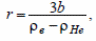
где b – отношение массы оболочки к ее площади.
Плотности гелия и воздуха: 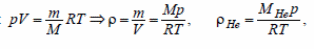
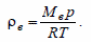
Радиус: 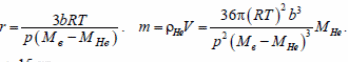
Ответ: m ≈ 15 кг.
29. Для изохорного процесса имеем: 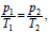 Т2 − температура газа после охлаждения. (1)
Т2 − температура газа после охлаждения. (1)
Первый закон термодинамики для этого процесса: 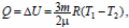 R − универсальная газовая постоянная. (2)
R − универсальная газовая постоянная. (2)
Решая систему из полученных двух уравнений, находим: 
Ответ: μ ≈ 0,004 кг/моль.
30. Для изохорного процесса имеем: 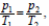 (Т2 − температура газа после охлаждения). (1)
(Т2 − температура газа после охлаждения). (1)
Первый закон термодинамики для этого процесса: 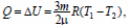 (R − универсальная газовая постоянная) (2)
(R − универсальная газовая постоянная) (2)
Решая систему из полученных двух уравнений, находим 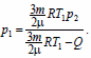
Ответ: р1 ≈ 4·105 Па.
31. 1) При медленном охлаждении газа он все время остается равновесным,поэтому можно пользоваться выражением для внутренней энергии одноатомного идеального газа
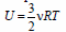
и уравнением Клапейрона–Менделеева pV = νRT .
Отсюда 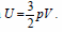
2) Поршень движется медленно, сил трения между поршнем и стенками сосуда нет, поэтому давление газа равно давлению окружающего воздуха (процесс изобарен).
3) Первое начало термодинамики для описания изобарного сжатия газа: Aвнешн = ΔU + |Q|,
где Aвнешн = pSx – работа внешних сил, 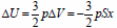 – изменение внутренней энергии одноатомного идеального газа при его изобарном сжатии, |Q| – количество теплоты, отведенное от газа при его охлаждении.
– изменение внутренней энергии одноатомного идеального газа при его изобарном сжатии, |Q| – количество теплоты, отведенное от газа при его охлаждении.
Отсюда 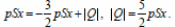
Ответ: |Q| = 75 Дж.
32. 1) При медленном охлаждении газа он все время остается равновесным, поэтому можно пользоваться выражением для внутренней энергии одноатомного идеального газа 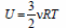
и уравнением Клапейрона–Менделеева pV = νRT .
Отсюда 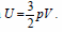
2) Поршень движется медленно, сил трения между поршнем и стенками сосуда нет, поэтому давление газа равно давлению окружающего воздуха (процесс изобарен).
3) Первое начало термодинамики для описания изобарного сжатия газа:Aвнешн = ΔU + |Q|,
где Aвнешн = pSx – работа внешних сил, 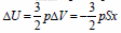 – изменение внутренней энергии одноатомного идеального газа при его изобарном сжатии, |Q| – количество теплоты, отведенное от газа при его охлаждении.
– изменение внутренней энергии одноатомного идеального газа при его изобарном сжатии, |Q| – количество теплоты, отведенное от газа при его охлаждении.
Отсюда 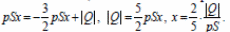
Ответ: x = 0,1 м.
33. 1) При медленном охлаждении газа он все время остается равновесным, поэтому можно пользоваться выражением для внутренней энергии одноатомного идеального газа 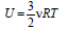
и уравнением Клапейрона–Менделеева pV = νRT .
Отсюда 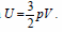
2) Поршень движется медленно, сил трения между поршнем и стенками сосуда нет, поэтому давление газа равно давлению окружающего воздуха (процесс изобарен).
3) Первое начало термодинамики для описания изобарного сжатия газа:Aвнешн = ΔU + |Q|,
где Aвнешн = pSx – работа внешних сил, 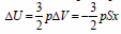 – изменение внутренней энергии одноатомного идеального газа при его изобарном сжатии, |Q| – количество теплоты, отведенное от газа при его охлаждении.
– изменение внутренней энергии одноатомного идеального газа при его изобарном сжатии, |Q| – количество теплоты, отведенное от газа при его охлаждении.
Отсюда 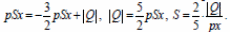
Ответ: S = 30 cм2.
34. 1) При медленном охлаждении газа он все время остается равновесным, поэтому можно пользоваться выражением для внутренней энергии одноатомного идеального газа 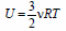
и уравнением Клапейрона–Менделеева pV = νRT .
Отсюда 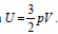
2) Поршень движется медленно, сил трения между поршнем и стенками сосуда нет, поэтому давление газа равно давлению окружающего воздуха (процесс изобарен).
3) Первое начало термодинамики для описания изобарного сжатия газа: Aвнешн = ΔU + |Q|, где Aвнешн = pSx – работа внешних сил, 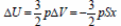 – изменение внутренней энергии одноатомного идеального газа при его изобарном сжатии, |Q| – количество теплоты,отведенное от газа при его охлаждении.
– изменение внутренней энергии одноатомного идеального газа при его изобарном сжатии, |Q| – количество теплоты,отведенное от газа при его охлаждении.
Отсюда 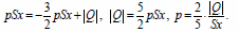
Ответ: p = 1,2·105 Па.
35. 1. Количество теплоты Q12, полученное газом на изобаре от нагревателя, согласно первому началу термодинамики,
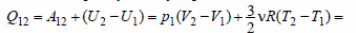
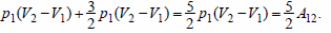
2. Модуль измерения внутренней энергии газа на адиабате |U3 −U1| = А13.
3. В результате 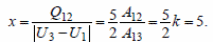
Ответ: х = 5.
36. 1. Количество теплоты Q12, полученное газом на изобаре от нагревателя, согласно первому началу термодинамики, равно
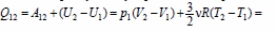
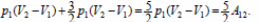
2. Модуль измерения внутренней энергии газа на адиабате |U3 −U1| = А13.
3. В результате 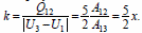
Отсюда следует, что х = 2/5 k = 2,4.





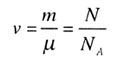
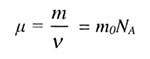
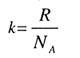
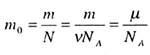
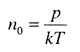
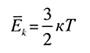
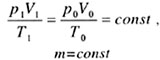
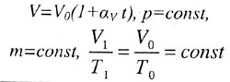
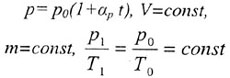



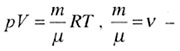 число молей
число молей 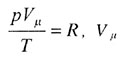 - молярный объем
- молярный объем 
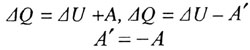
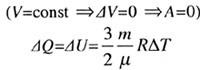





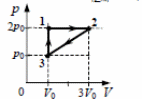










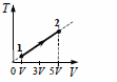


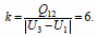 Чему равно отношение х работы газа на изобаре А12 к работе газа на адиабате А13 ?
Чему равно отношение х работы газа на изобаре А12 к работе газа на адиабате А13 ?
 1) Поршень будет медленно двигаться, если сила давления газа на поршень и сила трения со стороны стенок сосуда уравновесят друг друга: p2S =Fтр , откуда
1) Поршень будет медленно двигаться, если сила давления газа на поршень и сила трения со стороны стенок сосуда уравновесят друг друга: p2S =Fтр , откуда  1) Поршень будет медленно двигаться, если сила давления газа на поршень и сила трения со стороны стенок сосуда уравновесят друг друга: p2S = Fтр ,откуда
1) Поршень будет медленно двигаться, если сила давления газа на поршень и сила трения со стороны стенок сосуда уравновесят друг друга: p2S = Fтр ,откуда