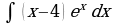Комплект контрольно-оценочных средств разработан на основе
Федерального государственного образовательного стандарта по специальности
среднего профессионального образования 23.02.07 Техническое обслуживание и ремонт двигателей, систем и агрегатов автомобилей, утвержденного приказом Министерства образования и науки от 9 декабря 2016 года № 1547 (зарегистрирован Министерством юстиции Российской Федерации 26 декабря 2016г., регистрационный №44936)
Просмотр содержимого документа
«Практическое занятие №4 Тема: «Нахождение неопределённых интегралов различными методами» (комплект КОС УЧЕБНОЙ ДИСЦИПЛИНЫ ЕН.01 МАТЕМАТИКА ДЛЯ СПЕЦИАЛЬНОСТИ СПО 23.02.07 ТЕХНИЧЕСКОЕ ОБСЛУЖИВАНИЕ И РЕМОНТ ДВИГАТЕЛЕЙ, СИСТЕМ И АГРЕГАТОВ АВТОМОБИЛЕЙ)»
Практическое занятие №4
Тема: «Нахождение неопределённых интегралов различными методами».
Цель: на конкретных примерах научиться находить неопределенный интеграл непосредственно с помощью таблицы интегралов (непосредственное интегрирование), методом замены переменной (методом подстановки), а также с помощью формулы интегрирования по частям.
Теоретические сведения к практической работе
Метод непосредственного интегрирования
Таблица интегралов
| 1.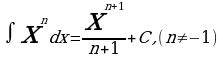
2. 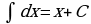
3. 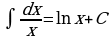
4. 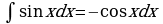
5. 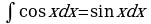
6. 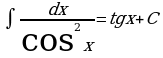 | 7. 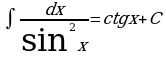
8. 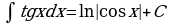
9. 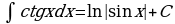
10. 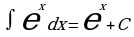
11. 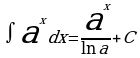
12. 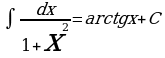 | 13. 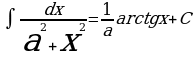
14.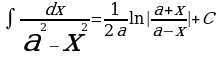
15. 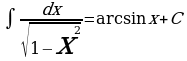
16. 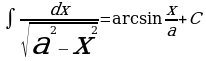 |
Пример 1: Вычислите 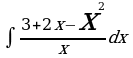
Решение: Для вычисления интеграла сначала каждый член числителя почленно разделим на знаменатель, затем воспользуемся 2 и 3 свойствами неопределенного интеграла и применим 1 и 3 табличные интегралы
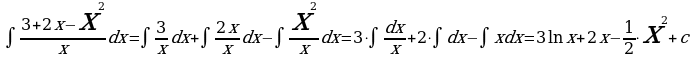
Метод замены переменной под знаком неопределенного интеграла
Суть этого метода состоит в том, что путем введения новой переменной интегрирования заданный интеграл сводится к новому интегралу, который легко вычисляется непосредственным интегрированием.
Применим подстановку х=j (t),
где j (t) – функция, имеющая непрерывную производную. Тогда f(x) = f[j(t)], dx=j' (t)dt и
òf(x)dx = ò f[j(t)]j' (t)dt (1)
Формула (1) называется формулой замены переменной в неопределенном интеграле.
Пример 1: Вычислить 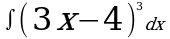
Решение: Введем новую переменную t = 3x-4, тогда 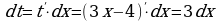 , откуда
, откуда 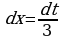 . Подставим новую переменную в интеграл (вместо выражения 3х-4 подставим t, вместо
. Подставим новую переменную в интеграл (вместо выражения 3х-4 подставим t, вместо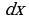 подставим
подставим 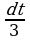 ).
). 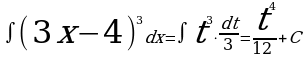
Далее нужно вернуться к первоначальной переменной. Для этого сделаем обратную замену (вместо t подставим выражение 3х-4), получим окончательный ответ.
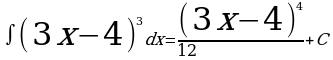
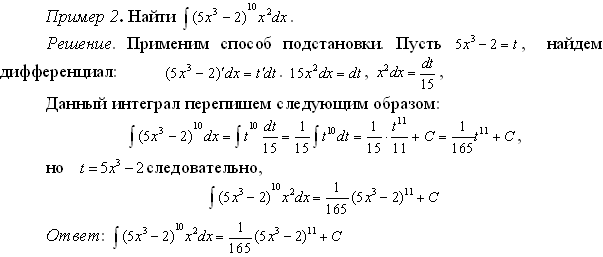
Интегрирование по частям
Формула интегрирования по частям имеет вид:
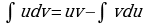
Вычисление интеграла 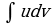 сводится к вычислению интеграла
сводится к вычислению интеграла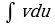 , если последний проще исходного.
, если последний проще исходного.
Для определения метода интегрирования необходимо руководствоваться следующим:
Применяем метод интегрирования по частям:
1) если подынтегральная функция задана в виде произведения различных функций (степенной и тригонометрической или в виде произведения многочлена на любую элементарную функции (логарифмическую; тригонометрическую; показательную и т.п.)
от логарифмической функции;
3)от обратных тригонометрических функций.
Содержание практической работы:
№ 1
| Вариант 1 | Вариант 2
|
| «3» | «4-5» | «3» | «4-5»
|
| а)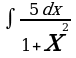 | а)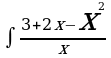 | а) 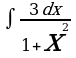 | а) 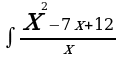
|
| б)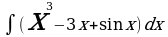 | б)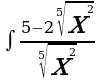 | б) 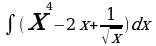 | б) 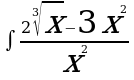
|
| в)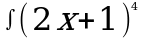 | в)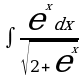 | в) 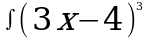 | в)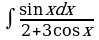
|
| г)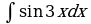 | г)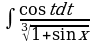 | г) 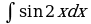 | г)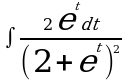
|
№2
1) 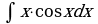 ; 2)
; 2) 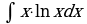 ; 3)
; 3) 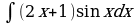
4)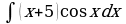 ; 5)
; 5) 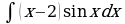 6)
6) 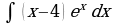







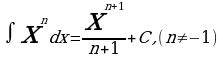
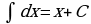
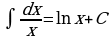
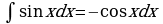
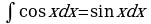
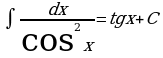
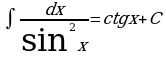
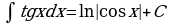
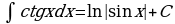
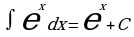
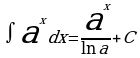
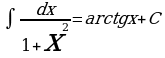
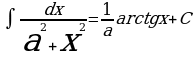
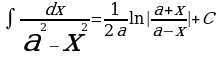
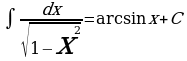
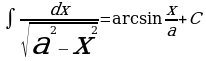
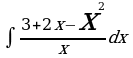
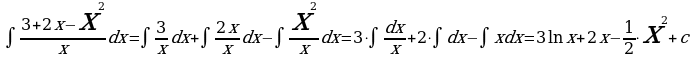
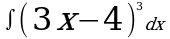
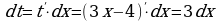 , откуда
, откуда 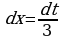 . Подставим новую переменную в интеграл (вместо выражения 3х-4 подставим t, вместо
. Подставим новую переменную в интеграл (вместо выражения 3х-4 подставим t, вместо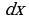 подставим
подставим 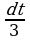 ).
). 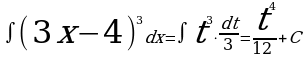
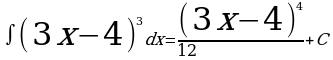
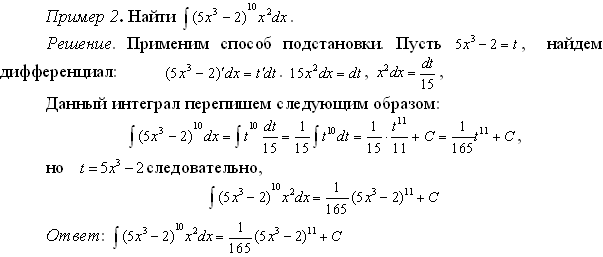
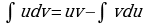
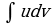 сводится к вычислению интеграла
сводится к вычислению интеграла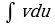 , если последний проще исходного.
, если последний проще исходного.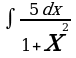
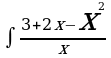
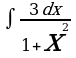
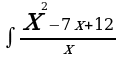
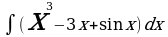
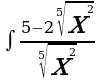
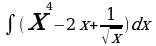
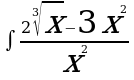
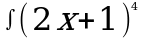
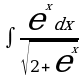
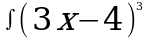
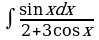
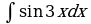
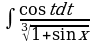
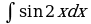
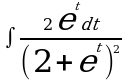
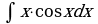 ; 2)
; 2) 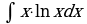 ; 3)
; 3) 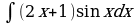
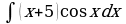 ; 5)
; 5) 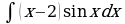 6)
6)