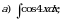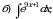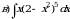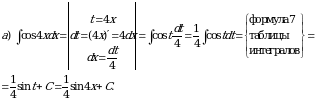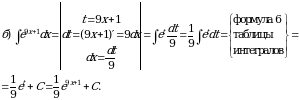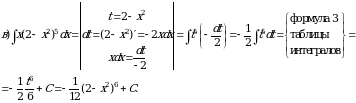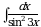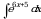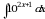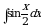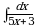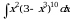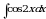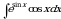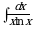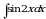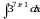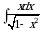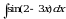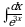СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока

Практическое занятие №7 Тема: «Вычисление неопределенных интегралов методом замены переменной» (комплект КОС УЧЕБНОЙ ДИСЦИПЛИНЫ ЕН.01 МАТЕМАТИКА ДЛЯ СПЕЦИАЛЬНОСТИ СПО 08.02.08 МОНТАЖ И ЭКСПЛУАТАЦИЯ ОБОРУДОВАНИЯ И СИСТЕМ ГАЗОСНАБЖЕНИЯ)
Категория:
Математика
07.12.2024 22:02




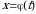 монотонная, непрерывно дифференцируемая функция, тогда
монотонная, непрерывно дифференцируемая функция, тогда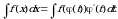 (1)
(1)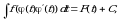 то
то 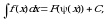 где
где 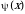 — функция, обратная
— функция, обратная 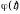 .
. с новой переменной
с новой переменной 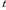 с помощью замены
с помощью замены 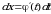 .
.