

СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока

Практические работы по дисциплине "Техническая механика" для СПО
Просмотр содержимого документа
«Пактическая работа №20»
Практическая работа №20
Расчет ременной передачи
Выполнить расчет клиноременной передачи, если задано:
| № варианта | Мощность валу редуктора Р, кВт | Частота вращения вала n, мин-1 | Передаточное число ременной передачи |
|
|
|
|
|
| ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ |
| ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ |
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
______________________________________________________________________
Просмотр содержимого документа
«Практическая работа №1»
Практическая работа №1
Плоская система сходящихся сил
Вариант №1
Задание
Определить величину и направление равнодействующей плоской системы сходящихся сил аналитическим способом, если задано F1 =10Н, F2 =8Н, F3 =4Н, F4=6Н
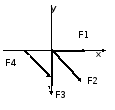
Рисунок 1 – Расчетная схема
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рисунок 2 – Построение направления равнодействующей
плоской системы сходящихся сил
Практическая работа №1
Плоская система сходящихся сил
Вариант №2
Задание
Определить величину и направление равнодействующей плоской системы сходящихся сил аналитическим способом, если задано F1 =10Н, F2 =8Н, F3 =4Н, F4=6Н

Рисунок 1 – Расчетная схема
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рисунок 2 – Построение направления равнодействующей
плоской системы сходящихся сил
Практическая работа №1
Плоская система сходящихся сил
Вариант №3
Задание
Определить величину и направление равнодействующей плоской системы сходящихся сил аналитическим способом, если задано F1 =10Н, F2 =8Н, F3 =4Н, F4=6Н

Рисунок 1 – Расчетная схема
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рисунок 2 – Построение направления равнодействующей
плоской системы сходящихся сил
Практическая работа №1
Плоская система сходящихся сил
Вариант №4
Задание
Определить величину и направление равнодействующей плоской системы сходящихся сил аналитическим способом, если задано F1 =10Н, F2 =8Н, F3 =4Н, F4=6Н

Рисунок 1 – Расчетная схема
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рисунок 2 – Построение направления равнодействующей
плоской системы сходящихся сил
Практическая работа №1
Плоская система сходящихся сил
 Вариант №5
Вариант №5
Задание
Определить величину и направление равнодействующей плоской системы сходящихся сил аналитическим способом, если задано F1 =10Н, F2 =8Н, F3 =4Н, F4=6Н

Рисунок 1 – Расчетная схема
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рисунок 2 – Построение направления равнодействующей
плоской системы сходящихся сил
Практическая работа №1
Плоская система сходящихся сил
Вариант №6
Задание
Определить величину и направление равнодействующей плоской системы сходящихся сил аналитическим способом, если задано F1 =10Н, F2 =8Н, F3 =4Н, F4=6Н

Рисунок 1 – Расчетная схема
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рисунок 2 – Построение направления равнодействующей
плоской системы сходящихся сил
Практическая работа №1
Плоская система сходящихся сил
Вариант №7
Задание
Определить величину и направление равнодействующей плоской системы сходящихся сил аналитическим способом, если задано F1 =10Н, F2 =8Н, F3 =4Н, F4=6Н

Рисунок 1 – Расчетная схема
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рисунок 2 – Построение направления равнодействующей
плоской системы сходящихся сил
Практическая работа №1
Плоская система сходящихся сил
Вариант №8
Задание
Определить величину и направление равнодействующей плоской системы сходящихся сил аналитическим способом, если задано F1 =10Н, F2 =8Н, F3 =4Н, F4=6Н

Рисунок 1 – Расчетная схема
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рисунок 2 – Построение направления равнодействующей
плоской системы сходящихся сил
Практическая работа №1
Плоская система сходящихся сил
 Вариант №9
Вариант №9
Задание
Определить величину и направление равнодействующей плоской системы сходящихся сил аналитическим способом, если задано F1 =10Н, F2 =8Н, F3 =4Н, F4=6Н

Рисунок 1 – Расчетная схема
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рисунок 2 – Построение направления равнодействующей
плоской системы сходящихся сил
Практическая работа №1
Плоская система сходящихся сил
Вариант №10
Задание
Определить величину и направление равнодействующей плоской системы сходящихся сил аналитическим способом, если задано F1 =10Н, F2 =8Н, F3 =4Н, F4=6Н

Рисунок 1 – Расчетная схема
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рисунок 2 – Построение направления равнодействующей
плоской системы сходящихся сил
Практическая работа №1
Плоская система сходящихся сил

 Вариант №11
Вариант №11
Задание
Определить величину и направление равнодействующей плоской системы сходящихся сил аналитическим способом, если задано F1 =10Н, F2 =8Н, F3 =4Н, F4=6Н

Рисунок 1 – Расчетная схема
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рисунок 2 – Построение направления равнодействующей
плоской системы сходящихся сил
Практическая работа №1
Плоская система сходящихся сил
Вариант №12
Задание
Определить величину и направление равнодействующей плоской системы сходящихся сил аналитическим способом, если задано F1 =10Н, F2 =8Н, F3 =4Н, F4=6Н

Рисунок 1 – Расчетная схема
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рисунок 2 – Построение направления равнодействующей
плоской системы сходящихся сил
Практическая работа №1
Плоская система сходящихся сил
Вариант №13
Задание
Определить величину и направление равнодействующей плоской системы сходящихся сил аналитическим способом, если задано F1 =10Н, F2 =8Н, F3 =4Н, F4=6Н

Рисунок 1 – Расчетная схема
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рисунок 2 – Построение направления равнодействующей
плоской системы сходящихся сил
Практическая работа №1
Плоская система сходящихся сил
Вариант №14
Задание
Определить величину и направление равнодействующей плоской системы сходящихся сил аналитическим способом, если задано F1 =10Н, F2 =8Н, F3 =4Н, F4=6Н

Рисунок 1 – Расчетная схема
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рисунок 2 – Построение направления равнодействующей
плоской системы сходящихся сил
Практическая работа №1
Плоская система сходящихся сил
Вариант №15
Задание
Определить величину и направление равнодействующей плоской системы сходящихся сил аналитическим способом, если задано F1 =10Н, F2 =8Н, F3 =4Н, F4=6Н

Рисунок 1 – Расчетная схема
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рисунок 2 – Построение направления равнодействующей
плоской системы сходящихся сил
Практическая работа №1
Плоская система сходящихся сил
Вариант №16
Задание
Определить величину и направление равнодействующей плоской системы сходящихся сил аналитическим способом, если задано F1 =10Н, F2 =8Н, F3 =4Н, F4=6Н
Рисунок 1 – Расчетная схема
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рисунок 2 – Построение направления равнодействующей
плоской системы сходящихся сил
Практическая работа №1
Плоская система сходящихся сил
Вариант №17
Задание
Определить величину и направление равнодействующей плоской системы сходящихся сил аналитическим способом, если задано F1 =10Н, F2 =8Н, F3 =4Н, F4=6Н
Рисунок 1 – Расчетная схема
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рисунок 2 – Построение направления равнодействующей
плоской системы сходящихся сил
Практическая работа №1
Плоская система сходящихся сил
Вариант №18
Задание
Определить величину и направление равнодействующей плоской системы сходящихся сил аналитическим способом, если задано F1 =10Н, F2 =8Н, F3 =4Н, F4=6Н
Рисунок 1 – Расчетная схема
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рисунок 2 – Построение направления равнодействующей
плоской системы сходящихся сил
Практическая работа №1
Плоская система сходящихся сил
Вариант №19
Задание
Определить величину и направление равнодействующей плоской системы сходящихся сил аналитическим способом, если задано F1 =10Н, F2 =8Н, F3 =4Н, F4=6Н
Рисунок 1 – Расчетная схема
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рисунок 2 – Построение направления равнодействующей
плоской системы сходящихся сил
Практическая работа №1
Плоская система сходящихся сил
Вариант №20
Задание
Определить величину и направление равнодействующей плоской системы сходящихся сил аналитическим способом, если задано F1 =10Н, F2 =8Н, F3 =4Н, F4=6Н
Рисунок 1 – Расчетная схема
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рисунок 2 – Построение направления равнодействующей
плоской системы сходящихся сил
Практическая работа №1
Плоская система сходящихся сил
Вариант №21
Задание
Определить величину и направление равнодействующей плоской системы сходящихся сил аналитическим способом, если задано F1 =10Н, F2 =8Н, F3 =4Н, F4=6Н
Рисунок 1 – Расчетная схема
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рисунок 2 – Построение направления равнодействующей
плоской системы сходящихся сил
Практическая работа №1
Плоская система сходящихся сил
Вариант №22
Задание
Определить величину и направление равнодействующей плоской системы сходящихся сил аналитическим способом, если задано F1 =10Н, F2 =8Н, F3 =4Н, F4=6Н
Рисунок 1 – Расчетная схема
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рисунок 2 – Построение направления равнодействующей
плоской системы сходящихся сил
Практическая работа №1
Плоская система сходящихся сил
Вариант №23
Задание
Определить величину и направление равнодействующей плоской системы сходящихся сил аналитическим способом, если задано F1 =10Н, F2 =8Н, F3 =4Н, F4=6Н
Рисунок 1 – Расчетная схема
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рисунок 2 – Построение направления равнодействующей
плоской системы сходящихся сил
Практическая работа №1
Плоская система сходящихся сил
Вариант №24
Задание у
Определить величину и направление равнодействующей плоской системы сходящихся сил аналитическим способом, если задано F1 =10Н, F2 =8Н, F3 =4Н, F4=6Н
Рисунок 1 – Расчетная схема
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рисунок 2 – Построение направления равнодействующей
плоской системы сходящихся сил
Практическая работа №1
Плоская система сходящихся сил
Вариант №25
Задание
Определить величину и направление равнодействующей плоской системы сходящихся сил аналитическим способом, если задано F1 =10Н, F2 =8Н, F3 =4Н, F4=6Н
Рисунок 1 – Расчетная схема
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рисунок 2 – Построение направления равнодействующей
плоской системы сходящихся сил
|
|
|
| ||
|
|
|
| ||
| у |
|
| ||
|
| 11 | 12 | ||
| 13 | 14 | х | ||
| 16 | 17 | 18 | ||
| 19 | 20 | 21 | ||
| 22 | 23 | 24 | ||
| 25 | 26 | 27 | ||
| 28 | 29 | 30 | ||
Просмотр содержимого документа
«Практическая работа №10»
Практическая работа №10
Расчеты на прочность и жесткость при растяжении и сжатии
Построить эпюры продольных сил, нормальных напряжений и эпюру перемещения сечений по длине бруса. Определить перемещение свободного конца бруса, коэффициенты запаса прочности, перемещения сечений. Двухступенчатый стальной брус нагружен силами F1, F2, F3. Площади поперечных сечений А1, А2. Принять Е = 2 105 МПА,
105 МПА,  МПА.
МПА.
| Вариант | F1, кН | F2, кН | F3, кН | А1, мм2 | А2, мм2 | а, м |
| 1 | 20 | 10 | 5 | 180 | 320 | 0,2 |
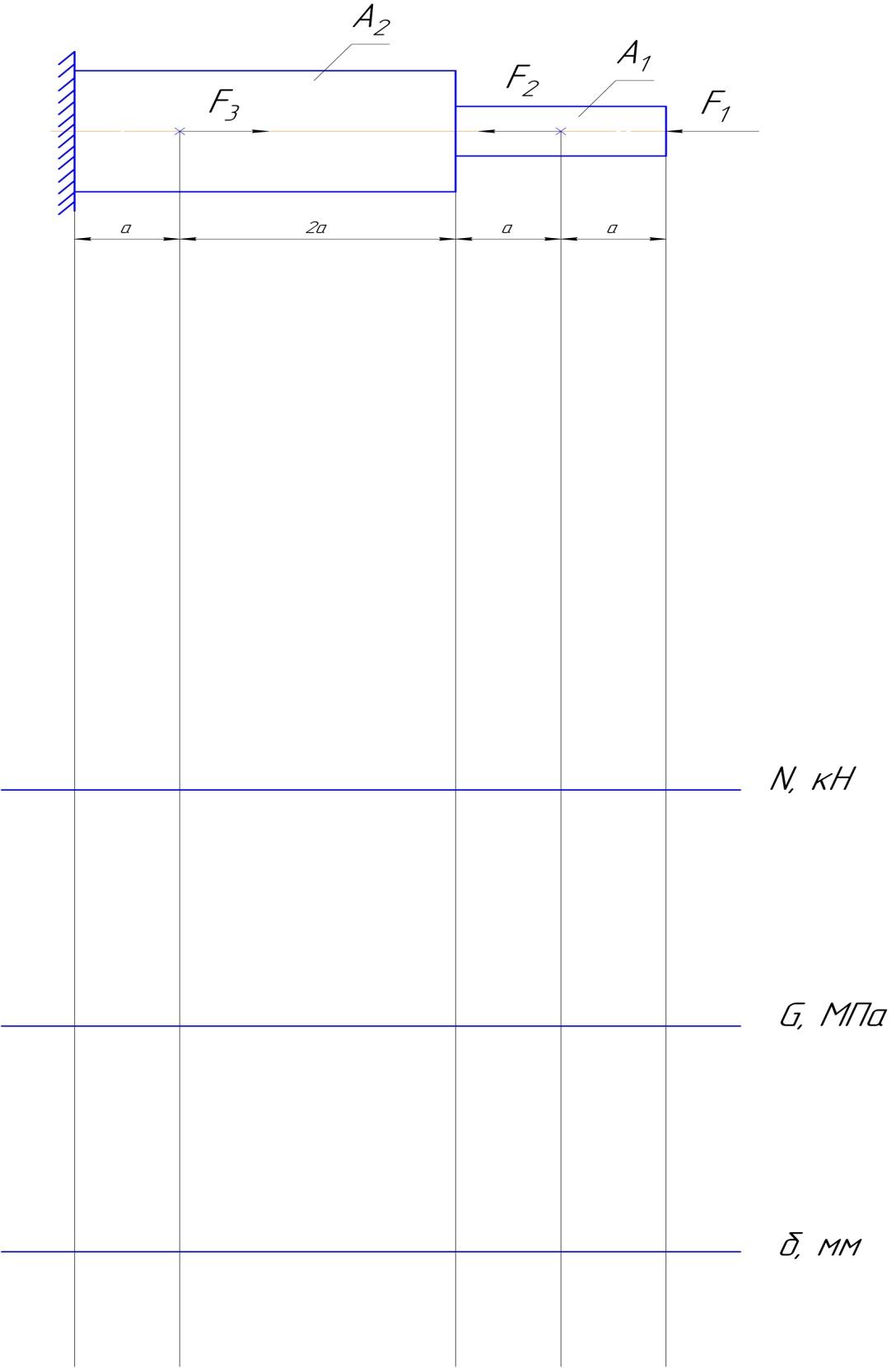
Рисунок 1 – Расчетная схема
1. Определение внутренних усилий (метод сечений)
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
2. Построение эпюры внутренних усилий (график, изображающий закон изменения внутренних усилий по длине бруса)
3. Определение напряжений на каждом из участков
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
4. Построение эпюры напряжений
5. Расчет коэффициентов запаса прочности по отношению к пределу текучести ([ ] = 1,3…2,2)
] = 1,3…2,2)
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
6. Расчет удлинения участков бруса
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
7. Расчет суммарного удлинения бруса (перемещение свободного конца)
__________________________________________________________________________________________________________________________________________________________________________
8. Расчет перемещения сечений
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
9. Построение эпюры перемещений
Практическая работа №10
Расчеты на прочность и жесткость при растяжении и сжатии
Построить эпюры продольных сил, нормальных напряжений и эпюру перемещения сечений по длине бруса. Определить перемещение свободного конца бруса, коэффициенты запаса прочности, перемещения сечений. Двухступенчатый стальной брус нагружен силами F1, F2, F3. Площади поперечных сечений А1, А2. Принять Е = 2 105 МПА,
105 МПА,  МПА.
МПА.
| Вариант | F1, кН | F2, кН | F3, кН | А1, мм2 | А2, мм2 | а, м |
| 2 | 26 | 20 | 10 | 160 | 240 | 0,4 |
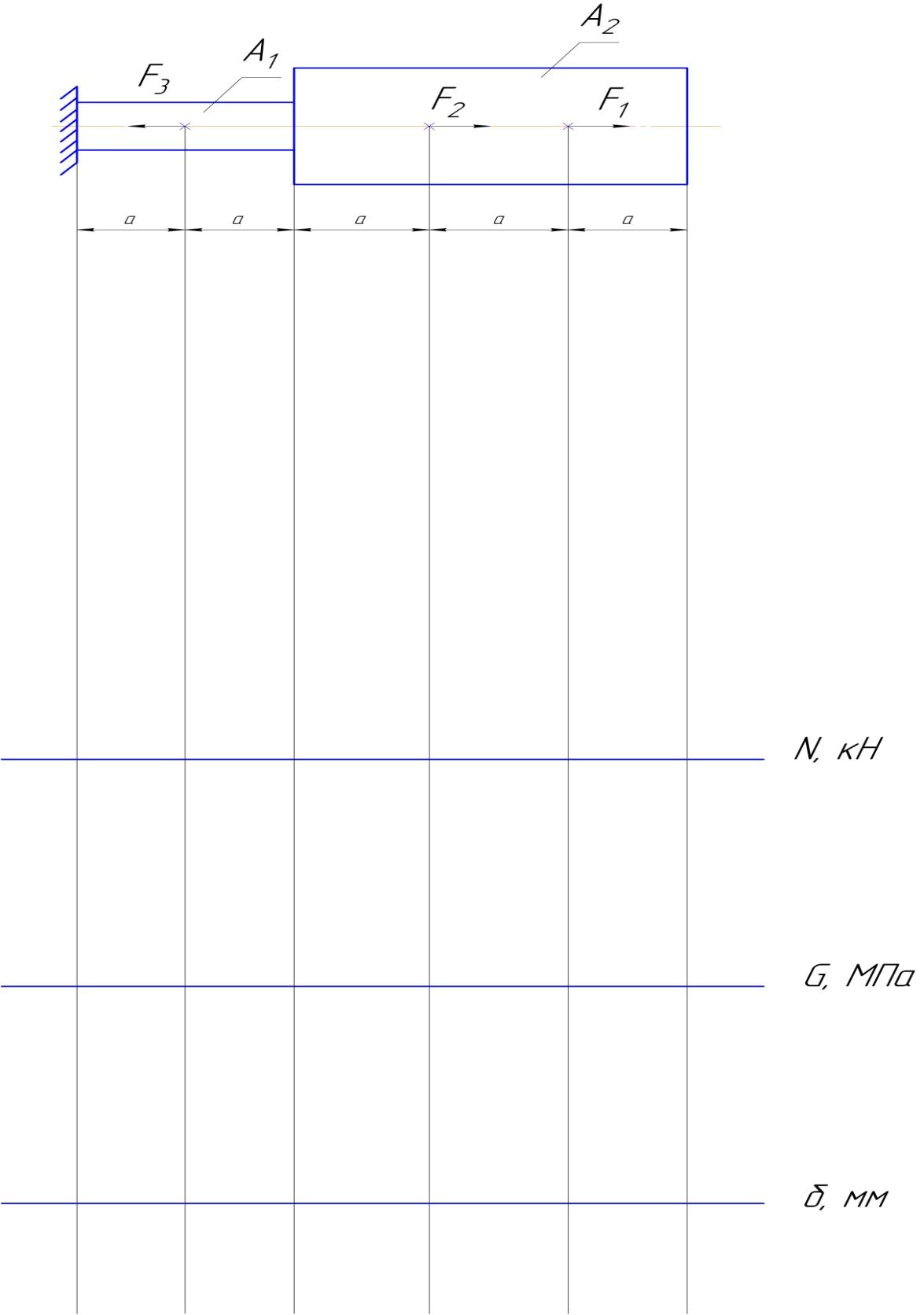
Рисунок 1 – Расчетная схема
1. Определение внутренних усилий (метод сечений)
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
2. Построение эпюры внутренних усилий (график, изображающий закон изменения внутренних усилий по длине бруса)
3. Определение напряжений на каждом из участков
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
4. Построение эпюры напряжений
5. Расчет коэффициентов запаса прочности по отношению к пределу текучести ([ ] = 1,3…2,2)
] = 1,3…2,2)
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
6. Расчет удлинения участков бруса
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
7. Расчет суммарного удлинения бруса (перемещение свободного конца)
__________________________________________________________________________________________________________________________________________________________________________
8. Расчет перемещения сечений
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
9. Построение эпюры перемещений
Практическая работа №10
Расчеты на прочность и жесткость при растяжении и сжатии
Построить эпюры продольных сил, нормальных напряжений и эпюру перемещения сечений по длине бруса. Определить перемещение свободного конца бруса, коэффициенты запаса прочности, перемещения сечений. Двухступенчатый стальной брус нагружен силами F1, F2, F3. Площади поперечных сечений А1, А2. Принять Е = 2 105 МПА,
105 МПА,  МПА.
МПА.
| Вариант | F1, кН | F2, кН | F3, кН | А1, мм2 | А2, мм2 | а, м |
| 3 | 20 | 8 | 4 | 100 | 150 | 0,4 |
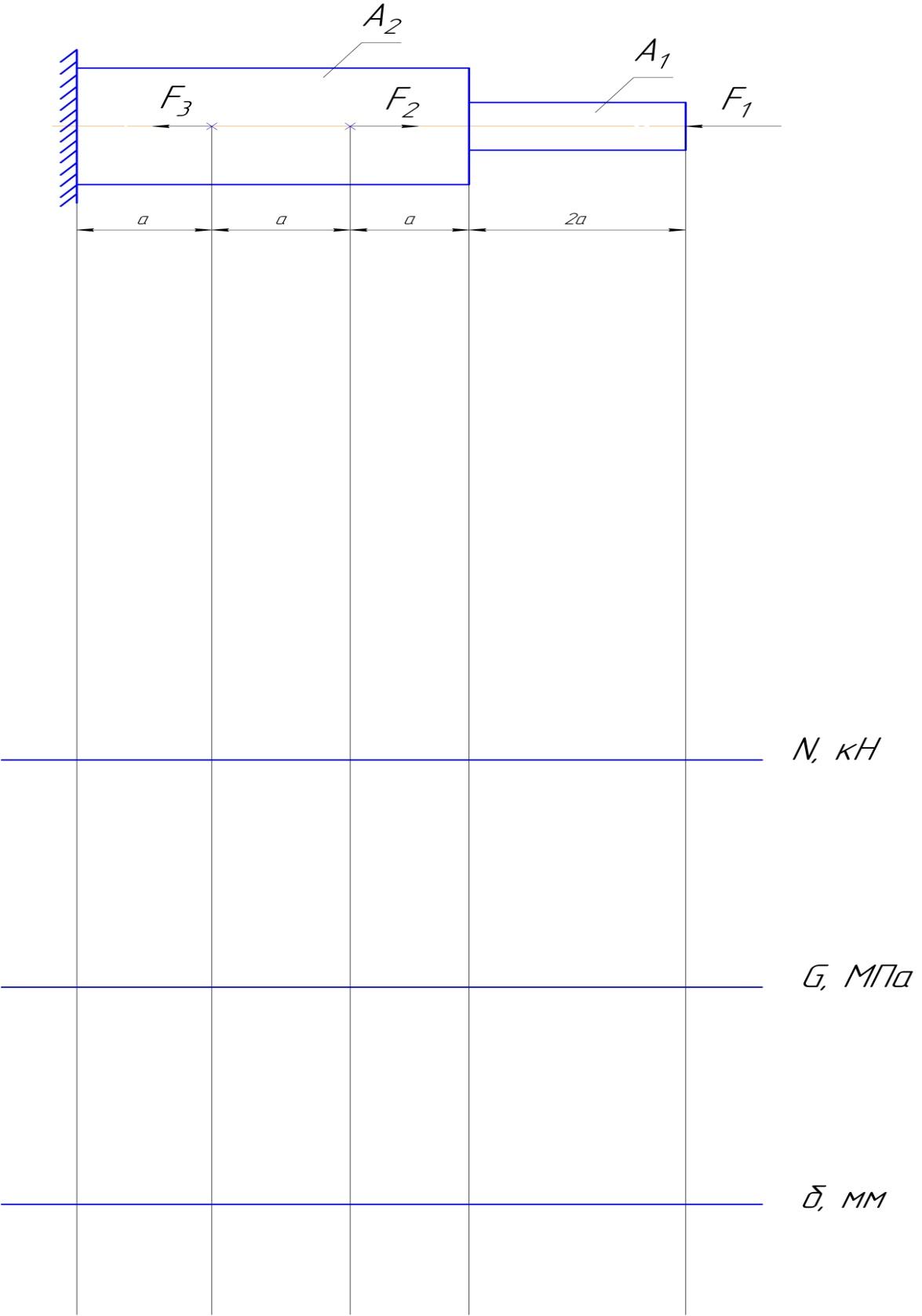
Рисунок 1 – Расчетная схема
1. Определение внутренних усилий (метод сечений)
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
2. Построение эпюры внутренних усилий (график, изображающий закон изменения внутренних усилий по длине бруса)
3. Определение напряжений на каждом из участков
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
4. Построение эпюры напряжений
5. Расчет коэффициентов запаса прочности по отношению к пределу текучести ([ ] = 1,3…2,2)
] = 1,3…2,2)
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
6. Расчет удлинения участков бруса
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
7. Расчет суммарного удлинения бруса (перемещение свободного конца)
__________________________________________________________________________________________________________________________________________________________________________
8. Расчет перемещения сечений
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
9. Построение эпюры перемещений
Практическая работа №10
Расчеты на прочность и жесткость при растяжении и сжатии
Построить эпюры продольных сил, нормальных напряжений и эпюру перемещения сечений по длине бруса. Определить перемещение свободного конца бруса, коэффициенты запаса прочности, перемещения сечений. Двухступенчатый стальной брус нагружен силами F1, F2, F3. Площади поперечных сечений А1, А2. Принять Е = 2 105 МПА,
105 МПА,  МПА.
МПА.
| Вариант | F1, кН | F2, кН | F3, кН | А1, мм2 | А2, мм2 | а, м |
| 4 | 17 | 13 | 8 | 200 | 250 | 0,5 |
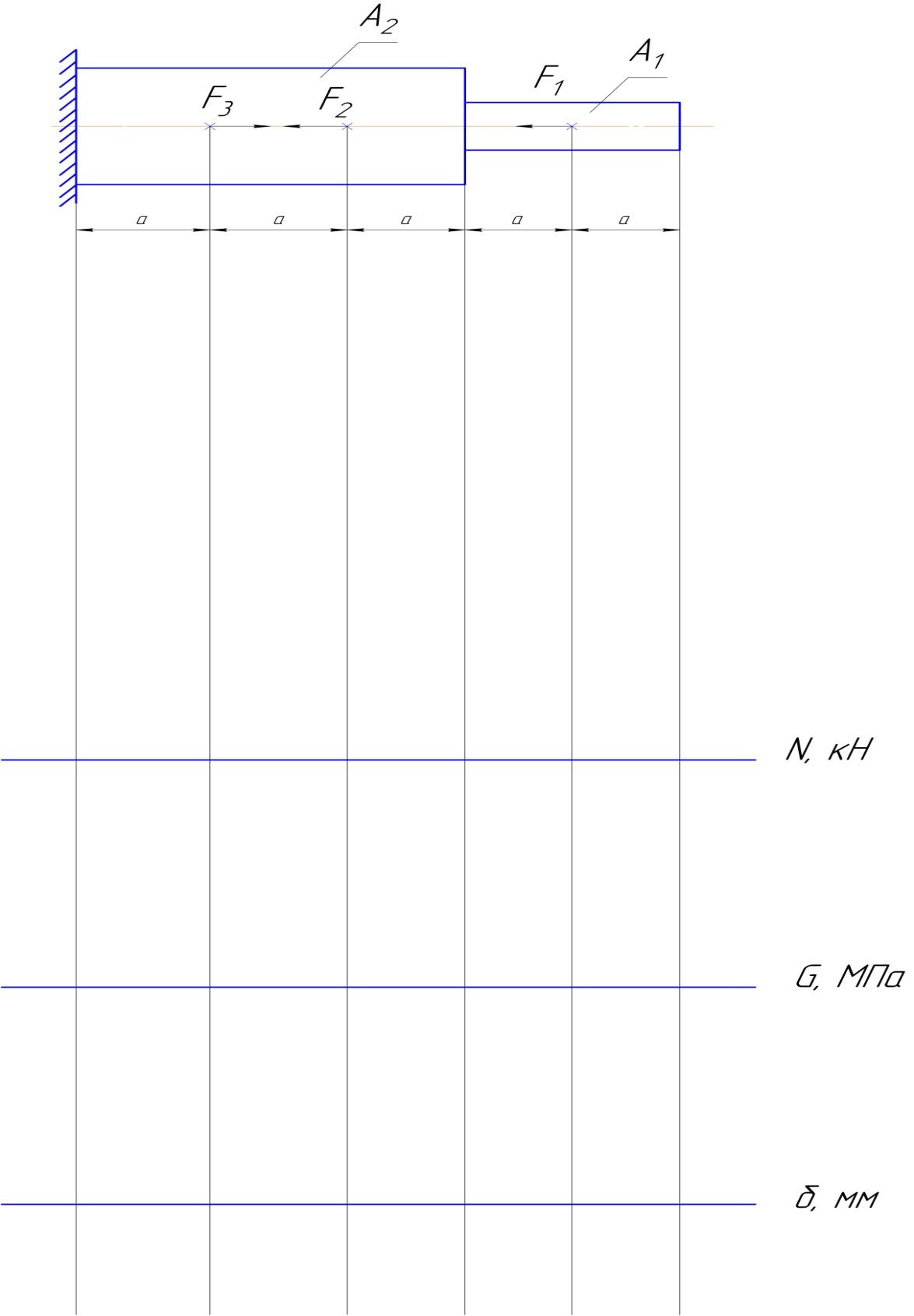
Рисунок 1 – Расчетная схема
1. Определение внутренних усилий (метод сечений)
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
2. Построение эпюры внутренних усилий (график, изображающий закон изменения внутренних усилий по длине бруса)
3. Определение напряжений на каждом из участков
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
4. Построение эпюры напряжений
5. Расчет коэффициентов запаса прочности по отношению к пределу текучести ([ ] = 1,3…2,2)
] = 1,3…2,2)
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
6. Расчет удлинения участков бруса
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
7. Расчет суммарного удлинения бруса (перемещение свободного конца)
__________________________________________________________________________________________________________________________________________________________________________
8. Расчет перемещения сечений
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
9. Построение эпюры перемещений
Практическая работа №10
Расчеты на прочность и жесткость при растяжении и сжатии
Построить эпюры продольных сил, нормальных напряжений и эпюру перемещения сечений по длине бруса. Определить перемещение свободного конца бруса, коэффициенты запаса прочности, перемещения сечений. Двухступенчатый стальной брус нагружен силами F1, F2, F3. Площади поперечных сечений А1, А2. Принять Е = 2 105 МПА,
105 МПА,  МПА.
МПА.
| Вариант | F1, кН | F2, кН | F3, кН | А1, мм2 | А2, мм2 | а, м |
| 5 | 16 | 25 | 28 | 120 | 280 | 0,6 |
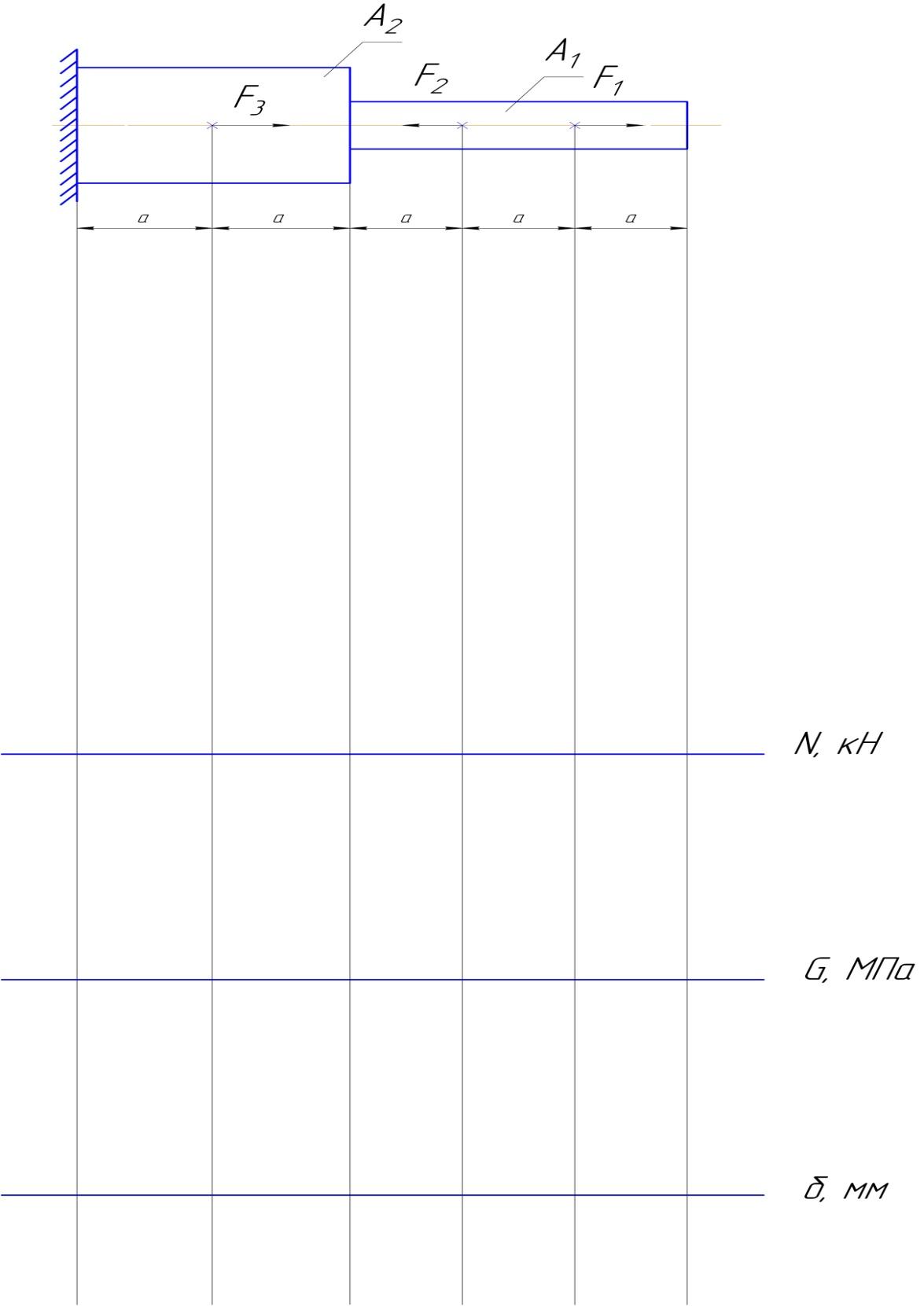
Рисунок 1 – Расчетная схема
1. Определение внутренних усилий (метод сечений)
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
2. Построение эпюры внутренних усилий (график, изображающий закон изменения внутренних усилий по длине бруса)
3. Определение напряжений на каждом из участков
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
4. Построение эпюры напряжений
5. Расчет коэффициентов запаса прочности по отношению к пределу текучести ([ ] = 1,3…2,2)
] = 1,3…2,2)
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
6. Расчет удлинения участков бруса
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
7. Расчет суммарного удлинения бруса (перемещение свободного конца)
__________________________________________________________________________________________________________________________________________________________________________
8. Расчет перемещения сечений
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
9. Построение эпюры перемещений
Практическая работа №10
Расчеты на прочность и жесткость при растяжении и сжатии
Построить эпюры продольных сил, нормальных напряжений и эпюру перемещения сечений по длине бруса. Определить перемещение свободного конца бруса, коэффициенты запаса прочности, перемещения сечений. Двухступенчатый стальной брус нагружен силами F1, F2, F3. Площади поперечных сечений А1, А2. Принять Е = 2 105 МПА,
105 МПА,  МПА.
МПА.
| Вариант | F1, кН | F2, кН | F3, кН | А1, мм2 | А2, мм2 | а, м |
| 6 | 10 | 12 | 13 | 90 | 170 | 0,4 |

Рисунок 1 – Расчетная схема
1. Определение внутренних усилий (метод сечений)
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
2. Построение эпюры внутренних усилий (график, изображающий закон изменения внутренних усилий по длине бруса)
3. Определение напряжений на каждом из участков
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
4. Построение эпюры напряжений
5. Расчет коэффициентов запаса прочности по отношению к пределу текучести ([ ] = 1,3…2,2)
] = 1,3…2,2)
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
6. Расчет удлинения участков бруса
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
7. Расчет суммарного удлинения бруса (перемещение свободного конца)
__________________________________________________________________________________________________________________________________________________________________________
8. Расчет перемещения сечений
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
9. Построение эпюры перемещений
Практическая работа №10
Расчеты на прочность и жесткость при растяжении и сжатии
Построить эпюры продольных сил, нормальных напряжений и эпюру перемещения сечений по длине бруса. Определить перемещение свободного конца бруса, коэффициенты запаса прочности, перемещения сечений. Двухступенчатый стальной брус нагружен силами F1, F2, F3. Площади поперечных сечений А1, А2. Принять Е = 2 105 МПА,
105 МПА,  МПА.
МПА.
| Вариант | F1, кН | F2, кН | F3, кН | А1, мм2 | А2, мм2 | а, м |
| 7 | 26 | 9 | 3 | 190 | 260 | 0,3 |

Рисунок 1 – Расчетная схема
1. Определение внутренних усилий (метод сечений)
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
2. Построение эпюры внутренних усилий (график, изображающий закон изменения внутренних усилий по длине бруса)
3. Определение напряжений на каждом из участков
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
4. Построение эпюры напряжений
5. Расчет коэффициентов запаса прочности по отношению к пределу текучести ([ ] = 1,3…2,2)
] = 1,3…2,2)
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
6. Расчет удлинения участков бруса
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
7. Расчет суммарного удлинения бруса (перемещение свободного конца)
__________________________________________________________________________________________________________________________________________________________________________
8. Расчет перемещения сечений
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
9. Построение эпюры перемещений
Практическая работа №10
Расчеты на прочность и жесткость при растяжении и сжатии
Построить эпюры продольных сил, нормальных напряжений и эпюру перемещения сечений по длине бруса. Определить перемещение свободного конца бруса, коэффициенты запаса прочности, перемещения сечений. Двухступенчатый стальной брус нагружен силами F1, F2, F3. Площади поперечных сечений А1, А2. Принять Е = 2 105 МПА,
105 МПА,  МПА.
МПА.
| Вариант | F1, кН | F2, кН | F3, кН | А1, мм2 | А2, мм2 | а, м |
| 8 | 40 | 55 | 24 | 280 | 340 | 0,2 |

Рисунок 1 – Расчетная схема
1. Определение внутренних усилий (метод сечений)
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
2. Построение эпюры внутренних усилий (график, изображающий закон изменения внутренних усилий по длине бруса)
3. Определение напряжений на каждом из участков
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
4. Построение эпюры напряжений
5. Расчет коэффициентов запаса прочности по отношению к пределу текучести ([ ] = 1,3…2,2)
] = 1,3…2,2)
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
6. Расчет удлинения участков бруса
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
7. Расчет суммарного удлинения бруса (перемещение свободного конца)
__________________________________________________________________________________________________________________________________________________________________________
8. Расчет перемещения сечений
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
9. Построение эпюры перемещений
Практическая работа №10
Расчеты на прочность и жесткость при растяжении и сжатии
Построить эпюры продольных сил, нормальных напряжений и эпюру перемещения сечений по длине бруса. Определить перемещение свободного конца бруса, коэффициенты запаса прочности, перемещения сечений. Двухступенчатый стальной брус нагружен силами F1, F2, F3. Площади поперечных сечений А1, А2. Принять Е = 2 105 МПА,
105 МПА,  МПА.
МПА.
| Вариант | F1, кН | F2, кН | F3, кН | А1, мм2 | А2, мм2 | а, м |
| 9 | 14 | 16 | 10 | 210 | 290 | 0,5 |

Рисунок 1 – Расчетная схема
1. Определение внутренних усилий (метод сечений)
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
2. Построение эпюры внутренних усилий (график, изображающий закон изменения внутренних усилий по длине бруса)
3. Определение напряжений на каждом из участков
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
4. Построение эпюры напряжений
5. Расчет коэффициентов запаса прочности по отношению к пределу текучести ([ ] = 1,3…2,2)
] = 1,3…2,2)
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
6. Расчет удлинения участков бруса
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
7. Расчет суммарного удлинения бруса (перемещение свободного конца)
__________________________________________________________________________________________________________________________________________________________________________
8. Расчет перемещения сечений
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
9. Построение эпюры перемещений
Практическая работа №10
Расчеты на прочность и жесткость при растяжении и сжатии
Построить эпюры продольных сил, нормальных напряжений и эпюру перемещения сечений по длине бруса. Определить перемещение свободного конца бруса, коэффициенты запаса прочности, перемещения сечений. Двухступенчатый стальной брус нагружен силами F1, F2, F3. Площади поперечных сечений А1, А2. Принять Е = 2 105 МПА,
105 МПА,  МПА.
МПА.
| Вариант | F1, кН | F2, кН | F3, кН | А1, мм2 | А2, мм2 | а, м |
| 10 | 28 | 14 | 5 | 190 | 240 | 0,6 |

Рисунок 1 – Расчетная схема
1. Определение внутренних усилий (метод сечений)
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
2. Построение эпюры внутренних усилий (график, изображающий закон изменения внутренних усилий по длине бруса)
3. Определение напряжений на каждом из участков
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
4. Построение эпюры напряжений
5. Расчет коэффициентов запаса прочности по отношению к пределу текучести ([ ] = 1,3…2,2)
] = 1,3…2,2)
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
6. Расчет удлинения участков бруса
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
7. Расчет суммарного удлинения бруса (перемещение свободного конца)
__________________________________________________________________________________________________________________________________________________________________________
8. Расчет перемещения сечений
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
9. Построение эпюры перемещений
Практическая работа №10
Расчеты на прочность и жесткость при растяжении и сжатии
Построить эпюры продольных сил, нормальных напряжений и эпюру перемещения сечений по длине бруса. Определить перемещение свободного конца бруса, коэффициенты запаса прочности, перемещения сечений. Двухступенчатый стальной брус нагружен силами F1, F2, F3. Площади поперечных сечений А1, А2. Принять Е = 2 105 МПА,
105 МПА,  МПА.
МПА.
| Вариант | F1, кН | F2, кН | F3, кН | А1, мм2 | А2, мм2 | а, м |
| 11 | 16 | 25 | 28 | 180 | 320 | 0,2 |

Рисунок 1 – Расчетная схема
1. Определение внутренних усилий (метод сечений)
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
2. Построение эпюры внутренних усилий (график, изображающий закон изменения внутренних усилий по длине бруса)
3. Определение напряжений на каждом из участков
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
4. Построение эпюры напряжений
5. Расчет коэффициентов запаса прочности по отношению к пределу текучести ([ ] = 1,3…2,2)
] = 1,3…2,2)
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
6. Расчет удлинения участков бруса
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
7. Расчет суммарного удлинения бруса (перемещение свободного конца)
__________________________________________________________________________________________________________________________________________________________________________
8. Расчет перемещения сечений
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
9. Построение эпюры перемещений
Практическая работа №10
Расчеты на прочность и жесткость при растяжении и сжатии
Построить эпюры продольных сил, нормальных напряжений и эпюру перемещения сечений по длине бруса. Определить перемещение свободного конца бруса, коэффициенты запаса прочности, перемещения сечений. Двухступенчатый стальной брус нагружен силами F1, F2, F3. Площади поперечных сечений А1, А2. Принять Е = 2 105 МПА,
105 МПА,  МПА.
МПА.
| Вариант | F1, кН | F2, кН | F3, кН | А1, мм2 | А2, мм2 | а, м |
| 12 | 10 | 12 | 13 | 160 | 240 | 0,3 |

Рисунок 1 – Расчетная схема
1. Определение внутренних усилий (метод сечений)
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
2. Построение эпюры внутренних усилий (график, изображающий закон изменения внутренних усилий по длине бруса)
3. Определение напряжений на каждом из участков
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
4. Построение эпюры напряжений
5. Расчет коэффициентов запаса прочности по отношению к пределу текучести ([ ] = 1,3…2,2)
] = 1,3…2,2)
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
6. Расчет удлинения участков бруса
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
7. Расчет суммарного удлинения бруса (перемещение свободного конца)
__________________________________________________________________________________________________________________________________________________________________________
8. Расчет перемещения сечений
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
9. Построение эпюры перемещений
Практическая работа №10
Расчеты на прочность и жесткость при растяжении и сжатии
Построить эпюры продольных сил, нормальных напряжений и эпюру перемещения сечений по длине бруса. Определить перемещение свободного конца бруса, коэффициенты запаса прочности, перемещения сечений. Двухступенчатый стальной брус нагружен силами F1, F2, F3. Площади поперечных сечений А1, А2. Принять Е = 2 105 МПА,
105 МПА,  МПА.
МПА.
| Вариант | F1, кН | F2, кН | F3, кН | А1, мм2 | А2, мм2 | а, м |
| 13 | 35 | 20 | 10 | 180 | 320 | 0,6 |

Рисунок 1 – Расчетная схема
1. Определение внутренних усилий (метод сечений)
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
2. Построение эпюры внутренних усилий (график, изображающий закон изменения внутренних усилий по длине бруса)
3. Определение напряжений на каждом из участков
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
4. Построение эпюры напряжений
5. Расчет коэффициентов запаса прочности по отношению к пределу текучести ([ ] = 1,3…2,2)
] = 1,3…2,2)
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
6. Расчет удлинения участков бруса
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
7. Расчет суммарного удлинения бруса (перемещение свободного конца)
__________________________________________________________________________________________________________________________________________________________________________
8. Расчет перемещения сечений
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
9. Построение эпюры перемещений
Практическая работа №10
Расчеты на прочность и жесткость при растяжении и сжатии
Построить эпюры продольных сил, нормальных напряжений и эпюру перемещения сечений по длине бруса. Определить перемещение свободного конца бруса, коэффициенты запаса прочности, перемещения сечений. Двухступенчатый стальной брус нагружен силами F1, F2, F3. Площади поперечных сечений А1, А2. Принять Е = 2 105 МПА,
105 МПА,  МПА.
МПА.
| Вариант | F1, кН | F2, кН | F3, кН | А1, мм2 | А2, мм2 | а, м |
| 14 | 26 | 20 | 10 | 200 | 250 | 0,5 |

Рисунок 1 – Расчетная схема
1. Определение внутренних усилий (метод сечений)
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
2. Построение эпюры внутренних усилий (график, изображающий закон изменения внутренних усилий по длине бруса)
3. Определение напряжений на каждом из участков
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
4. Построение эпюры напряжений
5. Расчет коэффициентов запаса прочности по отношению к пределу текучести ([ ] = 1,3…2,2)
] = 1,3…2,2)
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
6. Расчет удлинения участков бруса
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
7. Расчет суммарного удлинения бруса (перемещение свободного конца)
__________________________________________________________________________________________________________________________________________________________________________
8. Расчет перемещения сечений
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
9. Построение эпюры перемещений
Практическая работа №10
Расчеты на прочность и жесткость при растяжении и сжатии
Построить эпюры продольных сил, нормальных напряжений и эпюру перемещения сечений по длине бруса. Определить перемещение свободного конца бруса, коэффициенты запаса прочности, перемещения сечений. Двухступенчатый стальной брус нагружен силами F1, F2, F3. Площади поперечных сечений А1, А2. Принять Е = 2 105 МПА,
105 МПА,  МПА.
МПА.
| Вариант | F1, кН | F2, кН | F3, кН | А1, мм2 | А2, мм2 | а, м |
| 15 | 30 | 10 | 5 | 100 | 150 | 0,3 |

Рисунок 1 – Расчетная схема
1. Определение внутренних усилий (метод сечений)
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
2. Построение эпюры внутренних усилий (график, изображающий закон изменения внутренних усилий по длине бруса)
3. Определение напряжений на каждом из участков
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
4. Построение эпюры напряжений
5. Расчет коэффициентов запаса прочности по отношению к пределу текучести ([ ] = 1,3…2,2)
] = 1,3…2,2)
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
6. Расчет удлинения участков бруса
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
7. Расчет суммарного удлинения бруса (перемещение свободного конца)
__________________________________________________________________________________________________________________________________________________________________________
8. Расчет перемещения сечений
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
9. Построение эпюры перемещений
Практическая работа №10
Расчеты на прочность и жесткость при растяжении и сжатии
Построить эпюры продольных сил, нормальных напряжений и эпюру перемещения сечений по длине бруса. Определить перемещение свободного конца бруса, коэффициенты запаса прочности, перемещения сечений. Двухступенчатый стальной брус нагружен силами F1, F2, F3. Площади поперечных сечений А1, А2. Принять Е = 2 105 МПА,
105 МПА,  МПА.
МПА.
| Вариант | F1, кН | F2, кН | F3, кН | А1, мм2 | А2, мм2 | а, м |
| 16 | 17 | 13 | 8 | 190 | 240 | 0,5 |

Рисунок 1 – Расчетная схема
1. Определение внутренних усилий (метод сечений)
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
2. Построение эпюры внутренних усилий (график, изображающий закон изменения внутренних усилий по длине бруса)
3. Определение напряжений на каждом из участков
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
4. Построение эпюры напряжений
5. Расчет коэффициентов запаса прочности по отношению к пределу текучести ([ ] = 1,3…2,2)
] = 1,3…2,2)
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
6. Расчет удлинения участков бруса
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
7. Расчет суммарного удлинения бруса (перемещение свободного конца)
__________________________________________________________________________________________________________________________________________________________________________
8. Расчет перемещения сечений
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
9. Построение эпюры перемещений
Практическая работа №10
Расчеты на прочность и жесткость при растяжении и сжатии
Построить эпюры продольных сил, нормальных напряжений и эпюру перемещения сечений по длине бруса. Определить перемещение свободного конца бруса, коэффициенты запаса прочности, перемещения сечений. Двухступенчатый стальной брус нагружен силами F1, F2, F3. Площади поперечных сечений А1, А2. Принять Е = 2 105 МПА,
105 МПА,  МПА.
МПА.
| Вариант | F1, кН | F2, кН | F3, кН | А1, мм2 | А2, мм2 | а, м |
| 17 | 14 | 16 | 10 | 120 | 280 | 0,6 |

Рисунок 1 – Расчетная схема
1. Определение внутренних усилий (метод сечений)
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
2. Построение эпюры внутренних усилий (график, изображающий закон изменения внутренних усилий по длине бруса)
3. Определение напряжений на каждом из участков
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
4. Построение эпюры напряжений
5. Расчет коэффициентов запаса прочности по отношению к пределу текучести ([ ] = 1,3…2,2)
] = 1,3…2,2)
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
6. Расчет удлинения участков бруса
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
7. Расчет суммарного удлинения бруса (перемещение свободного конца)
__________________________________________________________________________________________________________________________________________________________________________
8. Расчет перемещения сечений
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
9. Построение эпюры перемещений
Практическая работа №10
Расчеты на прочность и жесткость при растяжении и сжатии
Построить эпюры продольных сил, нормальных напряжений и эпюру перемещения сечений по длине бруса. Определить перемещение свободного конца бруса, коэффициенты запаса прочности, перемещения сечений. Двухступенчатый стальной брус нагружен силами F1, F2, F3. Площади поперечных сечений А1, А2. Принять Е = 2 105 МПА,
105 МПА,  МПА.
МПА.
| Вариант | F1, кН | F2, кН | F3, кН | А1, мм2 | А2, мм2 | а, м |
| 18 | 17 | 13 | 8 | 90 | 170 | 0,3 |

Рисунок 1 – Расчетная схема
1. Определение внутренних усилий (метод сечений)
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
2. Построение эпюры внутренних усилий (график, изображающий закон изменения внутренних усилий по длине бруса)
3. Определение напряжений на каждом из участков
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
4. Построение эпюры напряжений
5. Расчет коэффициентов запаса прочности по отношению к пределу текучести ([ ] = 1,3…2,2)
] = 1,3…2,2)
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
6. Расчет удлинения участков бруса
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
7. Расчет суммарного удлинения бруса (перемещение свободного конца)
__________________________________________________________________________________________________________________________________________________________________________
8. Расчет перемещения сечений
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
9. Построение эпюры перемещений
Практическая работа №10
Расчеты на прочность и жесткость при растяжении и сжатии
Построить эпюры продольных сил, нормальных напряжений и эпюру перемещения сечений по длине бруса. Определить перемещение свободного конца бруса, коэффициенты запаса прочности, перемещения сечений. Двухступенчатый стальной брус нагружен силами F1, F2, F3. Площади поперечных сечений А1, А2. Принять Е = 2 105 МПА,
105 МПА,  МПА.
МПА.
| Вариант | F1, кН | F2, кН | F3, кН | А1, мм2 | А2, мм2 | а, м |
| 19 | 26 | 9 | 3 | 90 | 170 | 0,4 |

Рисунок 1 – Расчетная схема
1. Определение внутренних усилий (метод сечений)
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
2. Построение эпюры внутренних усилий (график, изображающий закон изменения внутренних усилий по длине бруса)
3. Определение напряжений на каждом из участков
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
4. Построение эпюры напряжений
5. Расчет коэффициентов запаса прочности по отношению к пределу текучести ([ ] = 1,3…2,2)
] = 1,3…2,2)
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
6. Расчет удлинения участков бруса
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
7. Расчет суммарного удлинения бруса (перемещение свободного конца)
__________________________________________________________________________________________________________________________________________________________________________
8. Расчет перемещения сечений
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
9. Построение эпюры перемещений
Практическая работа №10
Расчеты на прочность и жесткость при растяжении и сжатии
Построить эпюры продольных сил, нормальных напряжений и эпюру перемещения сечений по длине бруса. Определить перемещение свободного конца бруса, коэффициенты запаса прочности, перемещения сечений. Двухступенчатый стальной брус нагружен силами F1, F2, F3. Площади поперечных сечений А1, А2. Принять Е = 2 105 МПА,
105 МПА,  МПА.
МПА.
| Вариант | F1, кН | F2, кН | F3, кН | А1, мм2 | А2, мм2 | а, м |
| 20 | 40 | 55 | 24 | 210 | 290 | 0,5 |

Рисунок 1 – Расчетная схема
1. Определение внутренних усилий (метод сечений)
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
2. Построение эпюры внутренних усилий (график, изображающий закон изменения внутренних усилий по длине бруса)
3. Определение напряжений на каждом из участков
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
4. Построение эпюры напряжений
5. Расчет коэффициентов запаса прочности по отношению к пределу текучести ([ ] = 1,3…2,2)
] = 1,3…2,2)
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
6. Расчет удлинения участков бруса
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
7. Расчет суммарного удлинения бруса (перемещение свободного конца)
__________________________________________________________________________________________________________________________________________________________________________
8. Расчет перемещения сечений
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
9. Построение эпюры перемещений
Практическая работа №10
Расчеты на прочность и жесткость при растяжении и сжатии
Построить эпюры продольных сил, нормальных напряжений и эпюру перемещения сечений по длине бруса. Определить перемещение свободного конца бруса, коэффициенты запаса прочности, перемещения сечений. Двухступенчатый стальной брус нагружен силами F1, F2, F3. Площади поперечных сечений А1, А2. Принять Е = 2 105 МПА,
105 МПА,  МПА.
МПА.
| Вариант | F1, кН | F2, кН | F3, кН | А1, мм2 | А2, мм2 | а, м |
| 21 | 20 | 10 | 5 | 210 | 290 | 0,4 |

Рисунок 1 – Расчетная схема
1. Определение внутренних усилий (метод сечений)
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
2. Построение эпюры внутренних усилий (график, изображающий закон изменения внутренних усилий по длине бруса)
3. Определение напряжений на каждом из участков
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
4. Построение эпюры напряжений
5. Расчет коэффициентов запаса прочности по отношению к пределу текучести ([ ] = 1,3…2,2)
] = 1,3…2,2)
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
6. Расчет удлинения участков бруса
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
7. Расчет суммарного удлинения бруса (перемещение свободного конца)
__________________________________________________________________________________________________________________________________________________________________________
8. Расчет перемещения сечений
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
9. Построение эпюры перемещений
Практическая работа №10
Расчеты на прочность и жесткость при растяжении и сжатии
Построить эпюры продольных сил, нормальных напряжений и эпюру перемещения сечений по длине бруса. Определить перемещение свободного конца бруса, коэффициенты запаса прочности, перемещения сечений. Двухступенчатый стальной брус нагружен силами F1, F2, F3. Площади поперечных сечений А1, А2. Принять Е = 2 105 МПА,
105 МПА,  МПА.
МПА.
| Вариант | F1, кН | F2, кН | F3, кН | А1, мм2 | А2, мм2 | а, м |
| 22 | 28 | 14 | 5 | 200 | 250 | 0,5 |

Рисунок 1 – Расчетная схема
1. Определение внутренних усилий (метод сечений)
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
2. Построение эпюры внутренних усилий (график, изображающий закон изменения внутренних усилий по длине бруса)
3. Определение напряжений на каждом из участков
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
4. Построение эпюры напряжений
5. Расчет коэффициентов запаса прочности по отношению к пределу текучести ([ ] = 1,3…2,2)
] = 1,3…2,2)
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
6. Расчет удлинения участков бруса
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
7. Расчет суммарного удлинения бруса (перемещение свободного конца)
__________________________________________________________________________________________________________________________________________________________________________
8. Расчет перемещения сечений
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
9. Построение эпюры перемещений
Практическая работа №10
Расчеты на прочность и жесткость при растяжении и сжатии
Построить эпюры продольных сил, нормальных напряжений и эпюру перемещения сечений по длине бруса. Определить перемещение свободного конца бруса, коэффициенты запаса прочности, перемещения сечений. Двухступенчатый стальной брус нагружен силами F1, F2, F3. Площади поперечных сечений А1, А2. Принять Е = 2 105 МПА,
105 МПА,  МПА.
МПА.
| Вариант | F1, кН | F2, кН | F3, кН | А1, мм2 | А2, мм2 | а, м |
| 23 | 17 | 13 | 8 | 180 | 320 | 0,3 |

Рисунок 1 – Расчетная схема
1. Определение внутренних усилий (метод сечений)
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
2. Построение эпюры внутренних усилий (график, изображающий закон изменения внутренних усилий по длине бруса)
3. Определение напряжений на каждом из участков
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
4. Построение эпюры напряжений
5. Расчет коэффициентов запаса прочности по отношению к пределу текучести ([ ] = 1,3…2,2)
] = 1,3…2,2)
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
6. Расчет удлинения участков бруса
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
7. Расчет суммарного удлинения бруса (перемещение свободного конца)
__________________________________________________________________________________________________________________________________________________________________________
8. Расчет перемещения сечений
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
9. Построение эпюры перемещений
Практическая работа №10
Расчеты на прочность и жесткость при растяжении и сжатии
Построить эпюры продольных сил, нормальных напряжений и эпюру перемещения сечений по длине бруса. Определить перемещение свободного конца бруса, коэффициенты запаса прочности, перемещения сечений. Двухступенчатый стальной брус нагружен силами F1, F2, F3. Площади поперечных сечений А1, А2. Принять Е = 2 105 МПА,
105 МПА,  МПА.
МПА.
| Вариант | F1, кН | F2, кН | F3, кН | А1, мм2 | А2, мм2 | а, м |
| 24 | 10 | 12 | 13 | 100 | 150 | 0,4 |

Рисунок 1 – Расчетная схема
1. Определение внутренних усилий (метод сечений)
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
2. Построение эпюры внутренних усилий (график, изображающий закон изменения внутренних усилий по длине бруса)
3. Определение напряжений на каждом из участков
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
4. Построение эпюры напряжений
5. Расчет коэффициентов запаса прочности по отношению к пределу текучести ([ ] = 1,3…2,2)
] = 1,3…2,2)
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
6. Расчет удлинения участков бруса
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
7. Расчет суммарного удлинения бруса (перемещение свободного конца)
__________________________________________________________________________________________________________________________________________________________________________
8. Расчет перемещения сечений
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
9. Построение эпюры перемещений
Практическая работа №10
Расчеты на прочность и жесткость при растяжении и сжатии
Построить эпюры продольных сил, нормальных напряжений и эпюру перемещения сечений по длине бруса. Определить перемещение свободного конца бруса, коэффициенты запаса прочности, перемещения сечений. Двухступенчатый стальной брус нагружен силами F1, F2, F3. Площади поперечных сечений А1, А2. Принять Е = 2 105 МПА,
105 МПА,  МПА.
МПА.
| Вариант | F1, кН | F2, кН | F3, кН | А1, мм2 | А2, мм2 | а, м |
| 25 | 20 | 15 | 5 | 90 | 170 | 0,3 |

Рисунок 1 – Расчетная схема
1. Определение внутренних усилий (метод сечений)
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
2. Построение эпюры внутренних усилий (график, изображающий закон изменения внутренних усилий по длине бруса)
3. Определение напряжений на каждом из участков
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
4. Построение эпюры напряжений
5. Расчет коэффициентов запаса прочности по отношению к пределу текучести ([ ] = 1,3…2,2)
] = 1,3…2,2)
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
6. Расчет удлинения участков бруса
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
7. Расчет суммарного удлинения бруса (перемещение свободного конца)
__________________________________________________________________________________________________________________________________________________________________________
8. Расчет перемещения сечений
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
9. Построение эпюры перемещений
Практическая работа №10
Расчеты на прочность и жесткость при растяжении и сжатии
Построить эпюры продольных сил, нормальных напряжений и эпюру перемещения сечений по длине бруса. Определить перемещение свободного конца бруса, коэффициенты запаса прочности, перемещения сечений. Двухступенчатый стальной брус нагружен силами F1, F2, F3. Площади поперечных сечений А1, А2. Принять Е = 2 105 МПА,
105 МПА,  МПА.
МПА.
| Вариант | F1, кН | F2, кН | F3, кН | А1, мм2 | А2, мм2 | а, м |
| 26 | 26 | 20 | 5 | 190 | 260 | 0,6 |

Рисунок 1 – Расчетная схема
1. Определение внутренних усилий (метод сечений)
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
2. Построение эпюры внутренних усилий (график, изображающий закон изменения внутренних усилий по длине бруса)
3. Определение напряжений на каждом из участков
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
4. Построение эпюры напряжений
5. Расчет коэффициентов запаса прочности по отношению к пределу текучести ([ ] = 1,3…2,2)
] = 1,3…2,2)
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
6. Расчет удлинения участков бруса
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
7. Расчет суммарного удлинения бруса (перемещение свободного конца)
__________________________________________________________________________________________________________________________________________________________________________
8. Расчет перемещения сечений
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
9. Построение эпюры перемещений
Практическая работа №10
Расчеты на прочность и жесткость при растяжении и сжатии
Построить эпюры продольных сил, нормальных напряжений и эпюру перемещения сечений по длине бруса. Определить перемещение свободного конца бруса, коэффициенты запаса прочности, перемещения сечений. Двухступенчатый стальной брус нагружен силами F1, F2, F3. Площади поперечных сечений А1, А2. Принять Е = 2 105 МПА,
105 МПА,  МПА.
МПА.
| Вариант | F1, кН | F2, кН | F3, кН | А1, мм2 | А2, мм2 | а, м |
| 27 | 26 | 20 | 10 | 100 | 150 | 0,4 |

Рисунок 1 – Расчетная схема
1. Определение внутренних усилий (метод сечений)
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
2. Построение эпюры внутренних усилий (график, изображающий закон изменения внутренних усилий по длине бруса)
3. Определение напряжений на каждом из участков
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
4. Построение эпюры напряжений
5. Расчет коэффициентов запаса прочности по отношению к пределу текучести ([ ] = 1,3…2,2)
] = 1,3…2,2)
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
6. Расчет удлинения участков бруса
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
7. Расчет суммарного удлинения бруса (перемещение свободного конца)
__________________________________________________________________________________________________________________________________________________________________________
8. Расчет перемещения сечений
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
9. Построение эпюры перемещений
Практическая работа №10
Расчеты на прочность и жесткость при растяжении и сжатии
Построить эпюры продольных сил, нормальных напряжений и эпюру перемещения сечений по длине бруса. Определить перемещение свободного конца бруса, коэффициенты запаса прочности, перемещения сечений. Двухступенчатый стальной брус нагружен силами F1, F2, F3. Площади поперечных сечений А1, А2. Принять Е = 2 105 МПА,
105 МПА,  МПА.
МПА.
| Вариант | F1, кН | F2, кН | F3, кН | А1, мм2 | А2, мм2 | а, м |
| 28 | 26 | 13 | 8 | 190 | 240 | 0,4 |

Рисунок 1 – Расчетная схема
1. Определение внутренних усилий (метод сечений)
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
2. Построение эпюры внутренних усилий (график, изображающий закон изменения внутренних усилий по длине бруса)
3. Определение напряжений на каждом из участков
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
4. Построение эпюры напряжений
5. Расчет коэффициентов запаса прочности по отношению к пределу текучести ([ ] = 1,3…2,2)
] = 1,3…2,2)
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
6. Расчет удлинения участков бруса
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
7. Расчет суммарного удлинения бруса (перемещение свободного конца)
__________________________________________________________________________________________________________________________________________________________________________
8. Расчет перемещения сечений
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
9. Построение эпюры перемещений
Практическая работа №10
Расчеты на прочность и жесткость при растяжении и сжатии
Построить эпюры продольных сил, нормальных напряжений и эпюру перемещения сечений по длине бруса. Определить перемещение свободного конца бруса, коэффициенты запаса прочности, перемещения сечений. Двухступенчатый стальной брус нагружен силами F1, F2, F3. Площади поперечных сечений А1, А2. Принять Е = 2 105 МПА,
105 МПА,  МПА.
МПА.
| Вариант | F1, кН | F2, кН | F3, кН | А1, мм2 | А2, мм2 | а, м |
| 29 | 10 | 25 | 28 | 200 | 250 | 0,5 |

Рисунок 1 – Расчетная схема
1. Определение внутренних усилий (метод сечений)
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
2. Построение эпюры внутренних усилий (график, изображающий закон изменения внутренних усилий по длине бруса)
3. Определение напряжений на каждом из участков
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
4. Построение эпюры напряжений
5. Расчет коэффициентов запаса прочности по отношению к пределу текучести ([ ] = 1,3…2,2)
] = 1,3…2,2)
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
6. Расчет удлинения участков бруса
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
7. Расчет суммарного удлинения бруса (перемещение свободного конца)
__________________________________________________________________________________________________________________________________________________________________________
8. Расчет перемещения сечений
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
9. Построение эпюры перемещений
Практическая работа №10
Расчеты на прочность и жесткость при растяжении и сжатии
Построить эпюры продольных сил, нормальных напряжений и эпюру перемещения сечений по длине бруса. Определить перемещение свободного конца бруса, коэффициенты запаса прочности, перемещения сечений. Двухступенчатый стальной брус нагружен силами F1, F2, F3. Площади поперечных сечений А1, А2. Принять Е = 2 105 МПА,
105 МПА,  МПА.
МПА.
| Вариант | F1, кН | F2, кН | F3, кН | А1, мм2 | А2, мм2 | а, м |
| 30 | 10 | 20 | 25 | 90 | 170 | 0,6 |

Рисунок 1 – Расчетная схема
1. Определение внутренних усилий (метод сечений)
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
2. Построение эпюры внутренних усилий (график, изображающий закон изменения внутренних усилий по длине бруса)
3. Определение напряжений на каждом из участков
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
4. Построение эпюры напряжений
5. Расчет коэффициентов запаса прочности по отношению к пределу текучести ([ ] = 1,3…2,2)
] = 1,3…2,2)
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
6. Расчет удлинения участков бруса
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
7. Расчет суммарного удлинения бруса (перемещение свободного конца)
__________________________________________________________________________________________________________________________________________________________________________
8. Расчет перемещения сечений
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
9. Построение эпюры перемещений
Просмотр содержимого документа
«Практическая работа №11»
Практическая работа №11
Практические расчеты на срез и смятие
Вариант №1
Задача №1
Определить потребное количество заклепок для передачи внешней нагрузки 110 кН. Заклепки расположить в один ряд. Проверить прочность соединяемых листов. Известно:  диаметр заклепок d=14 мм.
диаметр заклепок d=14 мм.
Решение
1. Определить количество заклепок из расчета на сдвиг (рис.1).
 рис. 1
рис. 1
Из условия прочности на сдвиг определяем количество заклепок:



z =
Таким образом, необходимо _____ заклепок.
2. Определить количество заклепок из расчета на смятие
Из условия прочности на смятие определяем количество заклепок:



z =
Таким образом, необходимо _____ заклепок.
3. Проверим прочность листов на растяжение. Проверяем тонкий лист. Отверстия под заклепки ослабляют сечение, рассчитываем площадь листа в месте, ослабленном отверстиями (рис. 2).
 рис. 2
рис. 2
 =
=
Условие прочности на растяжение:


Следовательно, прочность листа ____________________.
Задача №2
Проверить прочность заклепочного соединения на срез и смятие. Нагрузка на соединение 45кН,  , d=12мм,
, d=12мм,  =10мм.
=10мм.
Решение
1. Соединение двухсрезными заклепками последовательно воспринимается тремя заклепками в левом ряду, а затем тремя заклепками в правом ряду (рис. 3).
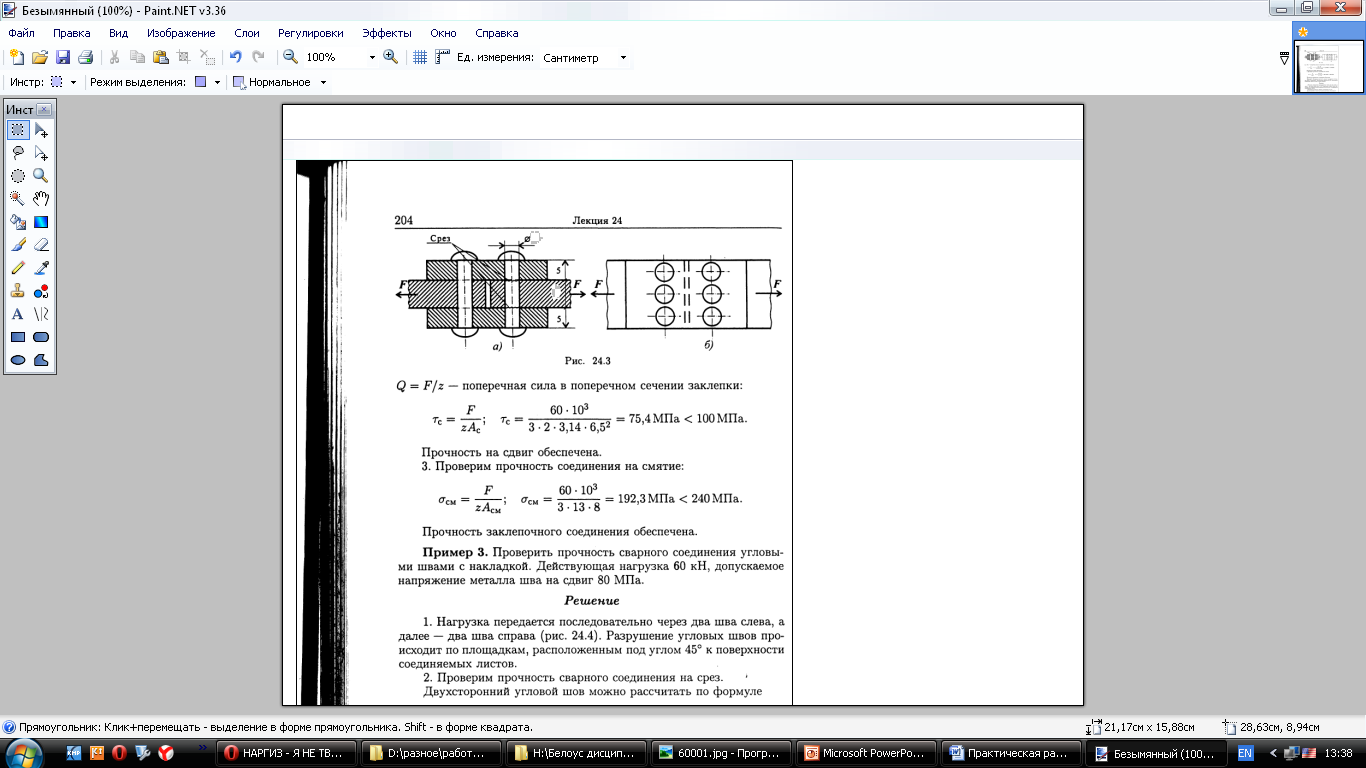 рис. 3
рис. 3
Площадь сдвига каждой заклепки: 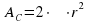 =
=
Площадь смятия боковой поверхности:  =
=
2. Проверим прочность соединения на сдвиг (срез).


Прочность на сдвиг ____________________.
3. Проверим прочность соединения на смятие.
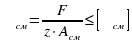
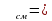
Прочность заклепочного соединения __________________.
Практическая работа №11
Практические расчеты на срез и смятие
Вариант №2
Задача №1
Определить потребное количество заклепок для передачи внешней нагрузки 100 кН. Заклепки расположить в один ряд. Проверить прочность соединяемых листов. Известно:  диаметр заклепок d=13 мм.
диаметр заклепок d=13 мм.
Решение
1. Определить количество заклепок из расчета на сдвиг (рис.1).
 рис. 1
рис. 1
Из условия прочности на сдвиг определяем количество заклепок:



z =
Таким образом, необходимо _____ заклепок.
2. Определить количество заклепок из расчета на смятие
Из условия прочности на смятие определяем количество заклепок:


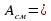
z =
Таким образом, необходимо _____ заклепок.
3. Проверим прочность листов на растяжение. Проверяем тонкий лист. Отверстия под заклепки ослабляют сечение, рассчитываем площадь листа в месте, ослабленном отверстиями (рис. 2).
 рис. 2
рис. 2
 =
=
Условие прочности на растяжение:


Следовательно, прочность листа ____________________.
Задача №2
Проверить прочность сварного соединения угловыми швами с накладкой. Действующая нагрузка 65 кН, допускаемое напряжение металла шва на сдвиг 70 МПа.
Решение
1. Нагрузка передается последовательно через два шва слева, а далее – два шва справа (рис.3). Разрушение угловых швов происходит по площадкам, расположенным под углом 450 к поверхности соединяемых листов.
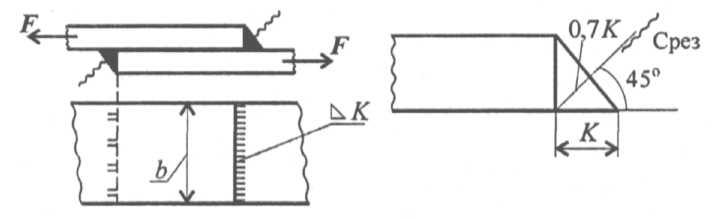 рис. 3
рис. 3
2. Проверим прочность сварного соединения на срез.

где Q=F
Расчетная площадь среза шва:
 ,
,
где К – катет шва, равен толщине накладки K=5мм;
b – длина шва b=110мм

Следовательно,

Прочность ____________________.
Практическая работа №11
Практические расчеты на срез и смятие
Вариант №3
Задача №1
Определить потребное количество заклепок для передачи внешней нагрузки 130 кН. Заклепки расположить в один ряд. Проверить прочность соединяемых листов. Известно:  диаметр заклепок d=18 мм.
диаметр заклепок d=18 мм.
Решение
1. Определить количество заклепок из расчета на сдвиг (рис.1).
 рис. 1
рис. 1
Из условия прочности на сдвиг определяем количество заклепок:



z =
Таким образом, необходимо _____ заклепок.
2. Определить количество заклепок из расчета на смятие
Из условия прочности на смятие определяем количество заклепок:



z =
Таким образом, необходимо _____ заклепок.
3. Проверим прочность листов на растяжение. Проверяем тонкий лист. Отверстия под заклепки ослабляют сечение, рассчитываем площадь листа в месте, ослабленном отверстиями (рис. 2).
 рис. 2
рис. 2
 =
=
Условие прочности на растяжение:


Следовательно, прочность листа ____________________.
Задача №2
Проверить прочность заклепочного соединения на срез и смятие. Нагрузка на соединение 40кН,  , d=10мм,
, d=10мм, 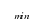 =8мм.
=8мм.
Решение
1. Соединение двухсрезными заклепками последовательно воспринимается тремя заклепками в левом ряду, а затем тремя заклепками в правом ряду (рис. 3).
 рис. 3
рис. 3
Площадь сдвига каждой заклепки: 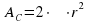 =
=
Площадь смятия боковой поверхности:  =
=
2. Проверим прочность соединения на сдвиг (срез).


Прочность на сдвиг ____________________.
3. Проверим прочность соединения на смятие.
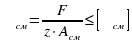
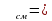
Прочность заклепочного соединения __________________.
Практическая работа №11
Практические расчеты на срез и смятие
Вариант №4
Задача №1
Определить потребное количество заклепок для передачи внешней нагрузки 90 кН. Заклепки расположить в один ряд. Проверить прочность соединяемых листов. Известно:  диаметр заклепок d=12 мм.
диаметр заклепок d=12 мм.
Решение
1. Определить количество заклепок из расчета на сдвиг (рис.1).
 рис. 1
рис. 1
Из условия прочности на сдвиг определяем количество заклепок:



z =
Таким образом, необходимо _____ заклепок.
2. Определить количество заклепок из расчета на смятие
Из условия прочности на смятие определяем количество заклепок:


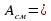
z =
Таким образом, необходимо _____ заклепок.
3. Проверим прочность листов на растяжение. Проверяем тонкий лист. Отверстия под заклепки ослабляют сечение, рассчитываем площадь листа в месте, ослабленном отверстиями (рис. 2).
 рис. 2
рис. 2
 =
=
Условие прочности на растяжение:


Следовательно, прочность листа ____________________.
Задача №2
Проверить прочность сварного соединения угловыми швами с накладкой. Действующая нагрузка 70 кН, допускаемое напряжение металла шва на сдвиг 85 МПа.
Решение
1. Нагрузка передается последовательно через два шва слева, а далее – два шва справа (рис.3). Разрушение угловых швов происходит по площадкам, расположенным под углом 450 к поверхности соединяемых листов.
 рис. 3
рис. 3
2. Проверим прочность сварного соединения на срез.

где Q=F
Расчетная площадь среза шва:
 ,
,
где К – катет шва, равен толщине накладки K=6мм;
b – длина шва b=125мм

Следовательно,

Прочность ____________________.
Практическая работа №11
Практические расчеты на срез и смятие
Вариант №5
Задача №1
Определить потребное количество заклепок для передачи внешней нагрузки 85 кН. Заклепки расположить в один ряд. Проверить прочность соединяемых листов. Известно:  диаметр заклепок d=10 мм.
диаметр заклепок d=10 мм.
Решение
1. Определить количество заклепок из расчета на сдвиг (рис.1).
 рис. 1
рис. 1
Из условия прочности на сдвиг определяем количество заклепок:



z =
Таким образом, необходимо _____ заклепок.
2. Определить количество заклепок из расчета на смятие
Из условия прочности на смятие определяем количество заклепок:



z =
Таким образом, необходимо _____ заклепок.
3. Проверим прочность листов на растяжение. Проверяем тонкий лист. Отверстия под заклепки ослабляют сечение, рассчитываем площадь листа в месте, ослабленном отверстиями (рис. 2).
 рис. 2
рис. 2
 =
=
Условие прочности на растяжение:


Следовательно, прочность листа ____________________.
Задача №2
Проверить прочность заклепочного соединения на срез и смятие. Нагрузка на соединение 50кН,  , d=14мм,
, d=14мм, 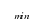 =10мм.
=10мм.
Решение
1. Соединение двухсрезными заклепками последовательно воспринимается тремя заклепками в левом ряду, а затем тремя заклепками в правом ряду (рис. 3).
 рис. 3
рис. 3
Площадь сдвига каждой заклепки: 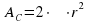 =
=
Площадь смятия боковой поверхности:  =
=
2. Проверим прочность соединения на сдвиг (срез).


Прочность на сдвиг ____________________.
3. Проверим прочность соединения на смятие.
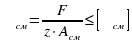
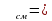
Прочность заклепочного соединения __________________.
Практическая работа №11
Практические расчеты на срез и смятие
Вариант №6
Задача №1
Определить потребное количество заклепок для передачи внешней нагрузки 110 кН. Заклепки расположить в один ряд. Проверить прочность соединяемых листов. Известно:  диаметр заклепок d=12 мм.
диаметр заклепок d=12 мм.
Решение
1. Определить количество заклепок из расчета на сдвиг (рис.1).
 рис. 1
рис. 1
Из условия прочности на сдвиг определяем количество заклепок:



z =
Таким образом, необходимо _____ заклепок.
2. Определить количество заклепок из расчета на смятие
Из условия прочности на смятие определяем количество заклепок:


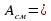
z =
Таким образом, необходимо _____ заклепок.
3. Проверим прочность листов на растяжение. Проверяем тонкий лист. Отверстия под заклепки ослабляют сечение, рассчитываем площадь листа в месте, ослабленном отверстиями (рис. 2).
 рис. 2
рис. 2
 =
=
Условие прочности на растяжение:


Следовательно, прочность листа ____________________.
Задача №2
Проверить прочность сварного соединения угловыми швами с накладкой. Действующая нагрузка 60 кН, допускаемое напряжение металла шва на сдвиг 80 МПа.
Решение
1. Нагрузка передается последовательно через два шва слева, а далее – два шва справа (рис.3). Разрушение угловых швов происходит по площадкам, расположенным под углом 450 к поверхности соединяемых листов.
 рис. 3
рис. 3
2. Проверим прочность сварного соединения на срез.

где Q=F
Расчетная площадь среза шва:
 ,
,
где К – катет шва, равен толщине накладки K=8мм;
b – длина шва b=140мм

Следовательно,

Прочность ____________________.
Практическая работа №11
Практические расчеты на срез и смятие
Вариант №7
Задача №1
Определить потребное количество заклепок для передачи внешней нагрузки 95 кН. Заклепки расположить в один ряд. Проверить прочность соединяемых листов. Известно:  диаметр заклепок d=12 мм.
диаметр заклепок d=12 мм.
Решение
1. Определить количество заклепок из расчета на сдвиг (рис.1).
 рис. 1
рис. 1
Из условия прочности на сдвиг определяем количество заклепок:



z =
Таким образом, необходимо _____ заклепок.
2. Определить количество заклепок из расчета на смятие
Из условия прочности на смятие определяем количество заклепок:



z =
Таким образом, необходимо _____ заклепок.
3. Проверим прочность листов на растяжение. Проверяем тонкий лист. Отверстия под заклепки ослабляют сечение, рассчитываем площадь листа в месте, ослабленном отверстиями (рис. 2).
 рис. 2
рис. 2
 =
=
Условие прочности на растяжение:


Следовательно, прочность листа ____________________.
Задача №2
Проверить прочность заклепочного соединения на срез и смятие. Нагрузка на соединение 65кН,  , d=16мм,
, d=16мм, 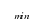 =10мм.
=10мм.
Решение
1. Соединение двухсрезными заклепками последовательно воспринимается тремя заклепками в левом ряду, а затем тремя заклепками в правом ряду (рис. 3).
 рис. 3
рис. 3
Площадь сдвига каждой заклепки: 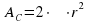 =
=
Площадь смятия боковой поверхности:  =
=
2. Проверим прочность соединения на сдвиг (срез).


Прочность на сдвиг ____________________.
3. Проверим прочность соединения на смятие.
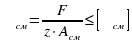
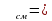
Прочность заклепочного соединения __________________.
Практическая работа №11
Практические расчеты на срез и смятие
Вариант №8
Задача №1
Определить потребное количество заклепок для передачи внешней нагрузки 150 кН. Заклепки расположить в один ряд. Проверить прочность соединяемых листов. Известно:  диаметр заклепок d=20 мм.
диаметр заклепок d=20 мм.
Решение
1. Определить количество заклепок из расчета на сдвиг (рис.1).
 рис. 1
рис. 1
Из условия прочности на сдвиг определяем количество заклепок:



z =
Таким образом, необходимо _____ заклепок.
2. Определить количество заклепок из расчета на смятие
Из условия прочности на смятие определяем количество заклепок:


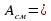
z =
Таким образом, необходимо _____ заклепок.
3. Проверим прочность листов на растяжение. Проверяем тонкий лист. Отверстия под заклепки ослабляют сечение, рассчитываем площадь листа в месте, ослабленном отверстиями (рис. 2).
 рис. 2
рис. 2
 =
=
Условие прочности на растяжение:


Следовательно, прочность листа ____________________.
Задача №2
Проверить прочность сварного соединения угловыми швами с накладкой. Действующая нагрузка 75 кН, допускаемое напряжение металла шва на сдвиг 90 МПа.
Решение
1. Нагрузка передается последовательно через два шва слева, а далее – два шва справа (рис.3). Разрушение угловых швов происходит по площадкам, расположенным под углом 450 к поверхности соединяемых листов.
 рис. 3
рис. 3
2. Проверим прочность сварного соединения на срез.

где Q=F
Расчетная площадь среза шва:
 ,
,
где К – катет шва, равен толщине накладки K=6мм;
b – длина шва b=125мм

Следовательно,

Прочность ____________________.
Практическая работа №11
Практические расчеты на срез и смятие
Вариант №9
Задача №1
Определить потребное количество заклепок для передачи внешней нагрузки 155 кН. Заклепки расположить в один ряд. Проверить прочность соединяемых листов. Известно:  диаметр заклепок d=21 мм.
диаметр заклепок d=21 мм.
Решение
1. Определить количество заклепок из расчета на сдвиг (рис.1).
 рис. 1
рис. 1
Из условия прочности на сдвиг определяем количество заклепок:



z =
Таким образом, необходимо _____ заклепок.
2. Определить количество заклепок из расчета на смятие
Из условия прочности на смятие определяем количество заклепок:



z =
Таким образом, необходимо _____ заклепок.
3. Проверим прочность листов на растяжение. Проверяем тонкий лист. Отверстия под заклепки ослабляют сечение, рассчитываем площадь листа в месте, ослабленном отверстиями (рис. 2).
 рис. 2
рис. 2
 =
=
Условие прочности на растяжение:


Следовательно, прочность листа ____________________.
Задача №2
Проверить прочность заклепочного соединения на срез и смятие. Нагрузка на соединение 70кН,  , d=18мм,
, d=18мм, 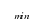 =12мм.
=12мм.
Решение
1. Соединение двухсрезными заклепками последовательно воспринимается тремя заклепками в левом ряду, а затем тремя заклепками в правом ряду (рис. 3).
 рис. 3
рис. 3
Площадь сдвига каждой заклепки: 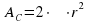 =
=
Площадь смятия боковой поверхности:  =
=
2. Проверим прочность соединения на сдвиг (срез).


Прочность на сдвиг ____________________.
3. Проверим прочность соединения на смятие.
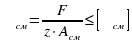
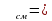
Прочность заклепочного соединения __________________.
Практическая работа №11
Практические расчеты на срез и смятие
Вариант №10
Задача №1
Определить потребное количество заклепок для передачи внешней нагрузки 80 кН. Заклепки расположить в один ряд. Проверить прочность соединяемых листов. Известно:  диаметр заклепок d=10 мм.
диаметр заклепок d=10 мм.
Решение
1. Определить количество заклепок из расчета на сдвиг (рис.1).
 рис. 1
рис. 1
Из условия прочности на сдвиг определяем количество заклепок:



z =
Таким образом, необходимо _____ заклепок.
2. Определить количество заклепок из расчета на смятие
Из условия прочности на смятие определяем количество заклепок:


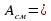
z =
Таким образом, необходимо _____ заклепок.
3. Проверим прочность листов на растяжение. Проверяем тонкий лист. Отверстия под заклепки ослабляют сечение, рассчитываем площадь листа в месте, ослабленном отверстиями (рис. 2).
 рис. 2
рис. 2
 =
=
Условие прочности на растяжение:


Следовательно, прочность листа ____________________.
Задача №2
Проверить прочность сварного соединения угловыми швами с накладкой. Действующая нагрузка 90 кН, допускаемое напряжение металла шва на сдвиг 100 МПа.
Решение
1. Нагрузка передается последовательно через два шва слева, а далее – два шва справа (рис.3). Разрушение угловых швов происходит по площадкам, расположенным под углом 450 к поверхности соединяемых листов.
 рис. 3
рис. 3
2. Проверим прочность сварного соединения на срез.

где Q=F
Расчетная площадь среза шва:
 ,
,
где К – катет шва, равен толщине накладки K=10мм;
b – длина шва b=145мм

Следовательно,

Прочность ____________________.
Практическая работа №11
Практические расчеты на срез и смятие
Вариант №11
Задача №1
Определить потребное количество заклепок для передачи внешней нагрузки 140 кН. Заклепки расположить в один ряд. Проверить прочность соединяемых листов. Известно:  диаметр заклепок d=18 мм.
диаметр заклепок d=18 мм.
Решение
1. Определить количество заклепок из расчета на сдвиг (рис.1).
 рис. 1
рис. 1
Из условия прочности на сдвиг определяем количество заклепок:



z =
Таким образом, необходимо _____ заклепок.
2. Определить количество заклепок из расчета на смятие
Из условия прочности на смятие определяем количество заклепок:



z =
Таким образом, необходимо _____ заклепок.
3. Проверим прочность листов на растяжение. Проверяем тонкий лист. Отверстия под заклепки ослабляют сечение, рассчитываем площадь листа в месте, ослабленном отверстиями (рис. 2).
 рис. 2
рис. 2
 =
=
Условие прочности на растяжение:


Следовательно, прочность листа ____________________.
Задача №2
Проверить прочность заклепочного соединения на срез и смятие. Нагрузка на соединение 60кН,  , d=12мм,
, d=12мм, 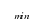 =16мм.
=16мм.
Решение
1. Соединение двухсрезными заклепками последовательно воспринимается тремя заклепками в левом ряду, а затем тремя заклепками в правом ряду (рис. 3).
 рис. 3
рис. 3
Площадь сдвига каждой заклепки: 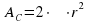 =
=
Площадь смятия боковой поверхности:  =
=
2. Проверим прочность соединения на сдвиг (срез).


Прочность на сдвиг ____________________.
3. Проверим прочность соединения на смятие.
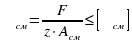
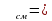
Прочность заклепочного соединения __________________.
Практическая работа №11
Практические расчеты на срез и смятие
Вариант №12
Задача №1
Определить потребное количество заклепок для передачи внешней нагрузки 152 кН. Заклепки расположить в один ряд. Проверить прочность соединяемых листов. Известно:  диаметр заклепок d=22 мм.
диаметр заклепок d=22 мм.
Решение
1. Определить количество заклепок из расчета на сдвиг (рис.1).
 рис. 1
рис. 1
Из условия прочности на сдвиг определяем количество заклепок:



z =
Таким образом, необходимо _____ заклепок.
2. Определить количество заклепок из расчета на смятие
Из условия прочности на смятие определяем количество заклепок:


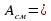
z =
Таким образом, необходимо _____ заклепок.
3. Проверим прочность листов на растяжение. Проверяем тонкий лист. Отверстия под заклепки ослабляют сечение, рассчитываем площадь листа в месте, ослабленном отверстиями (рис. 2).
 рис. 2
рис. 2
 =
=
Условие прочности на растяжение:


Следовательно, прочность листа ____________________.
Задача №2
Проверить прочность сварного соединения угловыми швами с накладкой. Действующая нагрузка 55 кН, допускаемое напряжение металла шва на сдвиг 70 МПа.
Решение
1. Нагрузка передается последовательно через два шва слева, а далее – два шва справа (рис.3). Разрушение угловых швов происходит по площадкам, расположенным под углом 450 к поверхности соединяемых листов.
 рис. 3
рис. 3
2. Проверим прочность сварного соединения на срез.

где Q=F
Расчетная площадь среза шва:
 ,
,
где К – катет шва, равен толщине накладки K=5мм;
b – длина шва b=110мм

Следовательно,

Прочность ____________________.
Практическая работа №11
Практические расчеты на срез и смятие
Вариант №13
Задача №1
Определить потребное количество заклепок для передачи внешней нагрузки 105 кН. Заклепки расположить в один ряд. Проверить прочность соединяемых листов. Известно:  диаметр заклепок d=14 мм.
диаметр заклепок d=14 мм.
Решение
1. Определить количество заклепок из расчета на сдвиг (рис.1).
 рис. 1
рис. 1
Из условия прочности на сдвиг определяем количество заклепок:



z =
Таким образом, необходимо _____ заклепок.
2. Определить количество заклепок из расчета на смятие
Из условия прочности на смятие определяем количество заклепок:



z =
Таким образом, необходимо _____ заклепок.
3. Проверим прочность листов на растяжение. Проверяем тонкий лист. Отверстия под заклепки ослабляют сечение, рассчитываем площадь листа в месте, ослабленном отверстиями (рис. 2).
 рис. 2
рис. 2
 =
=
Условие прочности на растяжение:


Следовательно, прочность листа ____________________.
Задача №2
Проверить прочность заклепочного соединения на срез и смятие. Нагрузка на соединение 65кН,  , d=16мм,
, d=16мм, 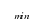 =12мм.
=12мм.
Решение
1. Соединение двухсрезными заклепками последовательно воспринимается тремя заклепками в левом ряду, а затем тремя заклепками в правом ряду (рис. 3).
 рис. 3
рис. 3
Площадь сдвига каждой заклепки: 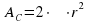 =
=
Площадь смятия боковой поверхности:  =
=
2. Проверим прочность соединения на сдвиг (срез).


Прочность на сдвиг ____________________.
3. Проверим прочность соединения на смятие.
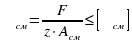
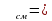
Прочность заклепочного соединения __________________.
Практическая работа №11
Практические расчеты на срез и смятие
Вариант №14
Задача №1
Определить потребное количество заклепок для передачи внешней нагрузки 160 кН. Заклепки расположить в один ряд. Проверить прочность соединяемых листов. Известно:  диаметр заклепок d=24 мм.
диаметр заклепок d=24 мм.
Решение
1. Определить количество заклепок из расчета на сдвиг (рис.1).
 рис. 1
рис. 1
Из условия прочности на сдвиг определяем количество заклепок:



z =
Таким образом, необходимо _____ заклепок.
2. Определить количество заклепок из расчета на смятие
Из условия прочности на смятие определяем количество заклепок:


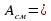
z =
Таким образом, необходимо _____ заклепок.
3. Проверим прочность листов на растяжение. Проверяем тонкий лист. Отверстия под заклепки ослабляют сечение, рассчитываем площадь листа в месте, ослабленном отверстиями (рис. 2).
 рис. 2
рис. 2
 =
=
Условие прочности на растяжение:


Следовательно, прочность листа ____________________.
Задача №2
Проверить прочность сварного соединения угловыми швами с накладкой. Действующая нагрузка 70 кН, допускаемое напряжение металла шва на сдвиг 80 МПа.
Решение
1. Нагрузка передается последовательно через два шва слева, а далее – два шва справа (рис.3). Разрушение угловых швов происходит по площадкам, расположенным под углом 450 к поверхности соединяемых листов.
 рис. 3
рис. 3
2. Проверим прочность сварного соединения на срез.

где Q=F
Расчетная площадь среза шва:
 ,
,
где К – катет шва, равен толщине накладки K=6мм;
b – длина шва b=125мм

Следовательно,

Прочность ____________________.
Практическая работа №11
Практические расчеты на срез и смятие
Вариант №15
Задача №1
Определить потребное количество заклепок для передачи внешней нагрузки 150 кН. Заклепки расположить в один ряд. Проверить прочность соединяемых листов. Известно:  диаметр заклепок d=22 мм.
диаметр заклепок d=22 мм.
Решение
1. Определить количество заклепок из расчета на сдвиг (рис.1).
 рис. 1
рис. 1
Из условия прочности на сдвиг определяем количество заклепок:



z =
Таким образом, необходимо _____ заклепок.
2. Определить количество заклепок из расчета на смятие
Из условия прочности на смятие определяем количество заклепок:



z =
Таким образом, необходимо _____ заклепок.
3. Проверим прочность листов на растяжение. Проверяем тонкий лист. Отверстия под заклепки ослабляют сечение, рассчитываем площадь листа в месте, ослабленном отверстиями (рис. 2).
 рис. 2
рис. 2
 =
=
Условие прочности на растяжение:


Следовательно, прочность листа ____________________.
Задача №2
Проверить прочность заклепочного соединения на срез и смятие. Нагрузка на соединение 40кН,  , d=10мм,
, d=10мм, 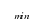 =10мм.
=10мм.
Решение
1. Соединение двухсрезными заклепками последовательно воспринимается тремя заклепками в левом ряду, а затем тремя заклепками в правом ряду (рис. 3).
 рис. 3
рис. 3
Площадь сдвига каждой заклепки: 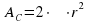 =
=
Площадь смятия боковой поверхности:  =
=
2. Проверим прочность соединения на сдвиг (срез).


Прочность на сдвиг ____________________.
3. Проверим прочность соединения на смятие.
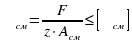
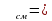
Прочность заклепочного соединения __________________.
Практическая работа №11
Практические расчеты на срез и смятие
Вариант №16
Задача №1
Определить потребное количество заклепок для передачи внешней нагрузки 80 кН. Заклепки расположить в один ряд. Проверить прочность соединяемых листов. Известно:  диаметр заклепок d=10 мм.
диаметр заклепок d=10 мм.
Решение
1. Определить количество заклепок из расчета на сдвиг (рис.1).
 рис. 1
рис. 1
Из условия прочности на сдвиг определяем количество заклепок:



z =
Таким образом, необходимо _____ заклепок.
2. Определить количество заклепок из расчета на смятие
Из условия прочности на смятие определяем количество заклепок:


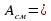
z =
Таким образом, необходимо _____ заклепок.
3. Проверим прочность листов на растяжение. Проверяем тонкий лист. Отверстия под заклепки ослабляют сечение, рассчитываем площадь листа в месте, ослабленном отверстиями (рис. 2).
 рис. 2
рис. 2
 =
=
Условие прочности на растяжение:


Следовательно, прочность листа ____________________.
Задача №2
Проверить прочность сварного соединения угловыми швами с накладкой. Действующая нагрузка 95 кН, допускаемое напряжение металла шва на сдвиг 100 МПа.
Решение
1. Нагрузка передается последовательно через два шва слева, а далее – два шва справа (рис.3). Разрушение угловых швов происходит по площадкам, расположенным под углом 450 к поверхности соединяемых листов.
 рис. 3
рис. 3
2. Проверим прочность сварного соединения на срез.

где Q=F
Расчетная площадь среза шва:
 ,
,
где К – катет шва, равен толщине накладки K=8мм;
b – длина шва b=140мм

Следовательно,

Прочность ____________________.
Практическая работа №11
Практические расчеты на срез и смятие
Вариант №17
Задача №1
Определить потребное количество заклепок для передачи внешней нагрузки 100 кН. Заклепки расположить в один ряд. Проверить прочность соединяемых листов. Известно:  диаметр заклепок d=12 мм.
диаметр заклепок d=12 мм.
Решение
1. Определить количество заклепок из расчета на сдвиг (рис.1).
 рис. 1
рис. 1
Из условия прочности на сдвиг определяем количество заклепок:



z =
Таким образом, необходимо _____ заклепок.
2. Определить количество заклепок из расчета на смятие
Из условия прочности на смятие определяем количество заклепок:



z =
Таким образом, необходимо _____ заклепок.
3. Проверим прочность листов на растяжение. Проверяем тонкий лист. Отверстия под заклепки ослабляют сечение, рассчитываем площадь листа в месте, ослабленном отверстиями (рис. 2).
 рис. 2
рис. 2
 =
=
Условие прочности на растяжение:


Следовательно, прочность листа ____________________.
Задача №2
Проверить прочность заклепочного соединения на срез и смятие. Нагрузка на соединение 45кН,  , d=10мм,
, d=10мм, 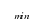 =8мм.
=8мм.
Решение
1. Соединение двухсрезными заклепками последовательно воспринимается тремя заклепками в левом ряду, а затем тремя заклепками в правом ряду (рис. 3).
 рис. 3
рис. 3
Площадь сдвига каждой заклепки: 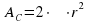 =
=
Площадь смятия боковой поверхности:  =
=
2. Проверим прочность соединения на сдвиг (срез).


Прочность на сдвиг ____________________.
3. Проверим прочность соединения на смятие.
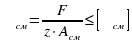
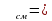
Прочность заклепочного соединения __________________.
Практическая работа №11
Практические расчеты на срез и смятие
Вариант №18
Задача №1
Определить потребное количество заклепок для передачи внешней нагрузки 160 кН. Заклепки расположить в один ряд. Проверить прочность соединяемых листов. Известно:  диаметр заклепок d=25 мм.
диаметр заклепок d=25 мм.
Решение
1. Определить количество заклепок из расчета на сдвиг (рис.1).
 рис. 1
рис. 1
Из условия прочности на сдвиг определяем количество заклепок:



z =
Таким образом, необходимо _____ заклепок.
2. Определить количество заклепок из расчета на смятие
Из условия прочности на смятие определяем количество заклепок:


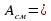
z =
Таким образом, необходимо _____ заклепок.
3. Проверим прочность листов на растяжение. Проверяем тонкий лист. Отверстия под заклепки ослабляют сечение, рассчитываем площадь листа в месте, ослабленном отверстиями (рис. 2).
 рис. 2
рис. 2
 =
=
Условие прочности на растяжение:


Следовательно, прочность листа ____________________.
Задача №2
Проверить прочность сварного соединения угловыми швами с накладкой. Действующая нагрузка 60 кН, допускаемое напряжение металла шва на сдвиг 75 МПа.
Решение
1. Нагрузка передается последовательно через два шва слева, а далее – два шва справа (рис.3). Разрушение угловых швов происходит по площадкам, расположенным под углом 450 к поверхности соединяемых листов.
 рис. 3
рис. 3
2. Проверим прочность сварного соединения на срез.

где Q=F
Расчетная площадь среза шва:
 ,
,
где К – катет шва, равен толщине накладки K=6мм;
b – длина шва b=125мм

Следовательно,

Прочность ____________________.
Практическая работа №11
Практические расчеты на срез и смятие
Вариант №19
Задача №1
Определить потребное количество заклепок для передачи внешней нагрузки 75 кН. Заклепки расположить в один ряд. Проверить прочность соединяемых листов. Известно:  диаметр заклепок d=10 мм.
диаметр заклепок d=10 мм.
Решение
1. Определить количество заклепок из расчета на сдвиг (рис.1).
 рис. 1
рис. 1
Из условия прочности на сдвиг определяем количество заклепок:



z =
Таким образом, необходимо _____ заклепок.
2. Определить количество заклепок из расчета на смятие
Из условия прочности на смятие определяем количество заклепок:



z =
Таким образом, необходимо _____ заклепок.
3. Проверим прочность листов на растяжение. Проверяем тонкий лист. Отверстия под заклепки ослабляют сечение, рассчитываем площадь листа в месте, ослабленном отверстиями (рис. 2).
 рис. 2
рис. 2
 =
=
Условие прочности на растяжение:


Следовательно, прочность листа ____________________.
Задача №2
Проверить прочность заклепочного соединения на срез и смятие. Нагрузка на соединение 75кН,  , d=18мм,
, d=18мм, 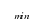 =12мм.
=12мм.
Решение
1. Соединение двухсрезными заклепками последовательно воспринимается тремя заклепками в левом ряду, а затем тремя заклепками в правом ряду (рис. 3).
 рис. 3
рис. 3
Площадь сдвига каждой заклепки: 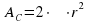 =
=
Площадь смятия боковой поверхности:  =
=
2. Проверим прочность соединения на сдвиг (срез).


Прочность на сдвиг ____________________.
3. Проверим прочность соединения на смятие.
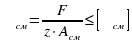
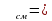
Прочность заклепочного соединения __________________.
Практическая работа №11
Практические расчеты на срез и смятие
Вариант №20
Задача №1
Определить потребное количество заклепок для передачи внешней нагрузки 100 кН. Заклепки расположить в один ряд. Проверить прочность соединяемых листов. Известно:  диаметр заклепок d=14 мм.
диаметр заклепок d=14 мм.
Решение
1. Определить количество заклепок из расчета на сдвиг (рис.1).
 рис. 1
рис. 1
Из условия прочности на сдвиг определяем количество заклепок:



z =
Таким образом, необходимо _____ заклепок.
2. Определить количество заклепок из расчета на смятие
Из условия прочности на смятие определяем количество заклепок:


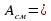
z =
Таким образом, необходимо _____ заклепок.
3. Проверим прочность листов на растяжение. Проверяем тонкий лист. Отверстия под заклепки ослабляют сечение, рассчитываем площадь листа в месте, ослабленном отверстиями (рис. 2).
 рис. 2
рис. 2
 =
=
Условие прочности на растяжение:


Следовательно, прочность листа ____________________.
Задача №2
Проверить прочность сварного соединения угловыми швами с накладкой. Действующая нагрузка 85 кН, допускаемое напряжение металла шва на сдвиг 95 МПа.
Решение
1. Нагрузка передается последовательно через два шва слева, а далее – два шва справа (рис.3). Разрушение угловых швов происходит по площадкам, расположенным под углом 450 к поверхности соединяемых листов.
 рис. 3
рис. 3
2. Проверим прочность сварного соединения на срез.

где Q=F
Расчетная площадь среза шва:
 ,
,
где К – катет шва, равен толщине накладки K=10мм;
b – длина шва b=145мм

Следовательно,

Прочность ____________________.
Практическая работа №11
Практические расчеты на срез и смятие
Вариант №21
Задача №1
Определить потребное количество заклепок для передачи внешней нагрузки 110 кН. Заклепки расположить в один ряд. Проверить прочность соединяемых листов. Известно:  диаметр заклепок d=12 мм.
диаметр заклепок d=12 мм.
Решение
1. Определить количество заклепок из расчета на сдвиг (рис.1).
 рис. 1
рис. 1
Из условия прочности на сдвиг определяем количество заклепок:



z =
Таким образом, необходимо _____ заклепок.
2. Определить количество заклепок из расчета на смятие
Из условия прочности на смятие определяем количество заклепок:



z =
Таким образом, необходимо _____ заклепок.
3. Проверим прочность листов на растяжение. Проверяем тонкий лист. Отверстия под заклепки ослабляют сечение, рассчитываем площадь листа в месте, ослабленном отверстиями (рис. 2).
 рис. 2
рис. 2
 =
=
Условие прочности на растяжение:


Следовательно, прочность листа ____________________.
Задача №2
Проверить прочность заклепочного соединения на срез и смятие. Нагрузка на соединение 45кН,  , d=10мм,
, d=10мм, 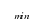 =8мм.
=8мм.
Решение
1. Соединение двухсрезными заклепками последовательно воспринимается тремя заклепками в левом ряду, а затем тремя заклепками в правом ряду (рис. 3).
 рис. 3
рис. 3
Площадь сдвига каждой заклепки: 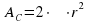 =
=
Площадь смятия боковой поверхности:  =
=
2. Проверим прочность соединения на сдвиг (срез).


Прочность на сдвиг ____________________.
3. Проверим прочность соединения на смятие.
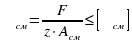
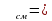
Прочность заклепочного соединения __________________.
Практическая работа №11
Практические расчеты на срез и смятие
Вариант №22
Задача №1
Определить потребное количество заклепок для передачи внешней нагрузки 135 кН. Заклепки расположить в один ряд. Проверить прочность соединяемых листов. Известно:  диаметр заклепок d=16 мм.
диаметр заклепок d=16 мм.
Решение
1. Определить количество заклепок из расчета на сдвиг (рис.1).
 рис. 1
рис. 1
Из условия прочности на сдвиг определяем количество заклепок:



z =
Таким образом, необходимо _____ заклепок.
2. Определить количество заклепок из расчета на смятие
Из условия прочности на смятие определяем количество заклепок:


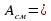
z =
Таким образом, необходимо _____ заклепок.
3. Проверим прочность листов на растяжение. Проверяем тонкий лист. Отверстия под заклепки ослабляют сечение, рассчитываем площадь листа в месте, ослабленном отверстиями (рис. 2).
 рис. 2
рис. 2
 =
=
Условие прочности на растяжение:


Следовательно, прочность листа ____________________.
Задача №2
Проверить прочность сварного соединения угловыми швами с накладкой. Действующая нагрузка 60 кН, допускаемое напряжение металла шва на сдвиг 75 МПа.
Решение
1. Нагрузка передается последовательно через два шва слева, а далее – два шва справа (рис.3). Разрушение угловых швов происходит по площадкам, расположенным под углом 450 к поверхности соединяемых листов.
 рис. 3
рис. 3
2. Проверим прочность сварного соединения на срез.

где Q=F
Расчетная площадь среза шва:
 ,
,
где К – катет шва, равен толщине накладки K=6мм;
b – длина шва b=125мм

Следовательно,

Прочность ____________________.
Практическая работа №11
Практические расчеты на срез и смятие
Вариант №23
Задача №1
Определить потребное количество заклепок для передачи внешней нагрузки 70 кН. Заклепки расположить в один ряд. Проверить прочность соединяемых листов. Известно:  диаметр заклепок d=10 мм.
диаметр заклепок d=10 мм.
Решение
1. Определить количество заклепок из расчета на сдвиг (рис.1).
 рис. 1
рис. 1
Из условия прочности на сдвиг определяем количество заклепок:



z =
Таким образом, необходимо _____ заклепок.
2. Определить количество заклепок из расчета на смятие
Из условия прочности на смятие определяем количество заклепок:



z =
Таким образом, необходимо _____ заклепок.
3. Проверим прочность листов на растяжение. Проверяем тонкий лист. Отверстия под заклепки ослабляют сечение, рассчитываем площадь листа в месте, ослабленном отверстиями (рис. 2).
 рис. 2
рис. 2
 =
=
Условие прочности на растяжение:


Следовательно, прочность листа ____________________.
Задача №2
Проверить прочность заклепочного соединения на срез и смятие. Нагрузка на соединение 60кН,  , d=14мм,
, d=14мм, 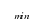 =12мм.
=12мм.
Решение
1. Соединение двухсрезными заклепками последовательно воспринимается тремя заклепками в левом ряду, а затем тремя заклепками в правом ряду (рис. 3).
 рис. 3
рис. 3
Площадь сдвига каждой заклепки: 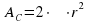 =
=
Площадь смятия боковой поверхности:  =
=
2. Проверим прочность соединения на сдвиг (срез).


Прочность на сдвиг ____________________.
3. Проверим прочность соединения на смятие.
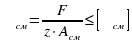
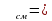
Прочность заклепочного соединения __________________.
Практическая работа №11
Практические расчеты на срез и смятие
Вариант №24
Задача №1
Определить потребное количество заклепок для передачи внешней нагрузки 152 кН. Заклепки расположить в один ряд. Проверить прочность соединяемых листов. Известно:  диаметр заклепок d=20 мм.
диаметр заклепок d=20 мм.
Решение
1. Определить количество заклепок из расчета на сдвиг (рис.1).
 рис. 1
рис. 1
Из условия прочности на сдвиг определяем количество заклепок:



z =
Таким образом, необходимо _____ заклепок.
2. Определить количество заклепок из расчета на смятие
Из условия прочности на смятие определяем количество заклепок:


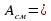
z =
Таким образом, необходимо _____ заклепок.
3. Проверим прочность листов на растяжение. Проверяем тонкий лист. Отверстия под заклепки ослабляют сечение, рассчитываем площадь листа в месте, ослабленном отверстиями (рис. 2).
 рис. 2
рис. 2
 =
=
Условие прочности на растяжение:


Следовательно, прочность листа ____________________.
Задача №2
Проверить прочность сварного соединения угловыми швами с накладкой. Действующая нагрузка 50 кН, допускаемое напряжение металла шва на сдвиг 70 МПа.
Решение
1. Нагрузка передается последовательно через два шва слева, а далее – два шва справа (рис.3). Разрушение угловых швов происходит по площадкам, расположенным под углом 450 к поверхности соединяемых листов.
 рис. 3
рис. 3
2. Проверим прочность сварного соединения на срез.

где Q=F
Расчетная площадь среза шва:
 ,
,
где К – катет шва, равен толщине накладки K=5мм;
b – длина шва b=110мм

Следовательно,

Прочность ____________________.
Практическая работа №11
Практические расчеты на срез и смятие
Вариант №25
Задача №1
Определить потребное количество заклепок для передачи внешней нагрузки 110 кН. Заклепки расположить в один ряд. Проверить прочность соединяемых листов. Известно:  диаметр заклепок d=14 мм.
диаметр заклепок d=14 мм.
Решение
1. Определить количество заклепок из расчета на сдвиг (рис.1).
 рис. 1
рис. 1
Из условия прочности на сдвиг определяем количество заклепок:



z =
Таким образом, необходимо _____ заклепок.
2. Определить количество заклепок из расчета на смятие
Из условия прочности на смятие определяем количество заклепок:



z =
Таким образом, необходимо _____ заклепок.
3. Проверим прочность листов на растяжение. Проверяем тонкий лист. Отверстия под заклепки ослабляют сечение, рассчитываем площадь листа в месте, ослабленном отверстиями (рис. 2).
 рис. 2
рис. 2
 =
=
Условие прочности на растяжение:


Следовательно, прочность листа ____________________.
Задача №2
Проверить прочность заклепочного соединения на срез и смятие. Нагрузка на соединение 45кН,  , d=12мм,
, d=12мм, 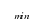 =10мм.
=10мм.
Решение
1. Соединение двухсрезными заклепками последовательно воспринимается тремя заклепками в левом ряду, а затем тремя заклепками в правом ряду (рис. 3).
 рис. 3
рис. 3
Площадь сдвига каждой заклепки: 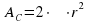 =
=
Площадь смятия боковой поверхности:  =
=
2. Проверим прочность соединения на сдвиг (срез).


Прочность на сдвиг ____________________.
3. Проверим прочность соединения на смятие.
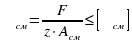
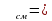
Прочность заклепочного соединения __________________.
Просмотр содержимого документа
«Практическая работа №12»
Практическая работа №12
Геометрические характеристики плоских сечений
Задача№1
Вычислить главные центральные моменты инерции сечения, представленного на схеме (рис.1). При расчетах воспользоваться данными таблицы.
| Вариант | d1, мм | d2, мм | h, мм | b, мм | a, мм | h1, мм | b1, мм | h2, мм |
| 1 | 72 | 12 | 72 | 36 | 48 | 16 | 32 | 6 |
 рис. 1
рис. 1
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Задача №2
Вычислить главные центральные моменты инерции составных сечений (рис.1). При расчете воспользоваться данными таблицы. Геометрические характеристики стали горячекатаной выбрать по ГОСТ 8239-89 (балки двутавровые) и ГОСТ 8240-89 (швеллеры).
| Вариант | № швеллера | № двутавра | a, мм | c, мм |
| 1 | 10 | 10 | 8 | 10 |
 рис.2
рис.2
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
Практическая работа №12
Геометрические характеристики плоских сечений
Задача№1
Вычислить главные центральные моменты инерции сечения, представленного на схеме (рис.1). При расчетах воспользоваться данными таблицы.
| Вариант | d1, мм | d2, мм | h, мм | b, мм | a, мм | h1, мм | b1, мм | h2, мм |
| 2 | 80 | 14 | 80 | 42 | 52 | 18 | 36 | 8 |
 рис. 1
рис. 1
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Задача №2
Вычислить главные центральные моменты инерции составных сечений (рис.1). При расчете воспользоваться данными таблицы. Геометрические характеристики стали горячекатаной выбрать по ГОСТ 8239-89 (балки двутавровые) и ГОСТ 8240-89 (швеллеры).
| Вариант | № швеллера | № двутавра | a, мм | c, мм |
| 2 | 12 | 12 | 10 | 15 |
 рис.2
рис.2
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
Практическая работа №12
Геометрические характеристики плоских сечений
Задача№1
Вычислить главные центральные моменты инерции сечения, представленного на схеме (рис.1). При расчетах воспользоваться данными таблицы.
| Вариант | d1, мм | d2, мм | h, мм | b, мм | a, мм | h1, мм | b1, мм | h2, мм |
| 3 | 88 | 16 | 88 | 48 | 56 | 20 | 40 | 10 |
 рис. 1
рис. 1
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Задача №2
Вычислить главные центральные моменты инерции составных сечений (рис.1). При расчете воспользоваться данными таблицы. Геометрические характеристики стали горячекатаной выбрать по ГОСТ 8239-89 (балки двутавровые) и ГОСТ 8240-89 (швеллеры).
| Вариант | № швеллера | № двутавра | a, мм | c, мм |
| 3 | 14 | 14 | 12 | 20 |
 рис.2
рис.2
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
Практическая работа №12
Геометрические характеристики плоских сечений
Задача№1
Вычислить главные центральные моменты инерции сечения, представленного на схеме (рис.1). При расчетах воспользоваться данными таблицы.
| Вариант | d1, мм | d2, мм | h, мм | b, мм | a, мм | h1, мм | b1, мм | h2, мм |
| 4 | 96 | 18 | 96 | 54 | 60 | 22 | 44 | 6 |
 рис. 1
рис. 1
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Задача №2
Вычислить главные центральные моменты инерции составных сечений (рис.1). При расчете воспользоваться данными таблицы. Геометрические характеристики стали горячекатаной выбрать по ГОСТ 8239-89 (балки двутавровые) и ГОСТ 8240-89 (швеллеры).
| Вариант | № швеллера | № двутавра | a, мм | c, мм |
| 4 | 16 | 16 | 14 | 25 |
 рис.2
рис.2
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
Практическая работа №12
Геометрические характеристики плоских сечений
Задача№1
Вычислить главные центральные моменты инерции сечения, представленного на схеме (рис.1). При расчетах воспользоваться данными таблицы.
| Вариант | d1, мм | d2, мм | h, мм | b, мм | a, мм | h1, мм | b1, мм | h2, мм |
| 5 | 98 | 10 | 98 | 60 | 58 | 24 | 48 | 8 |
 рис. 1
рис. 1
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Задача №2
Вычислить главные центральные моменты инерции составных сечений (рис.1). При расчете воспользоваться данными таблицы. Геометрические характеристики стали горячекатаной выбрать по ГОСТ 8239-89 (балки двутавровые) и ГОСТ 8240-89 (швеллеры).
| Вариант | № швеллера | № двутавра | a, мм | c, мм |
| 5 | 18 | 18 | 16 | 30 |
 рис.2
рис.2
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
Практическая работа №12
Геометрические характеристики плоских сечений
Задача№1
Вычислить главные центральные моменты инерции сечения, представленного на схеме (рис.1). При расчетах воспользоваться данными таблицы.
| Вариант | d1, мм | d2, мм | h, мм | b, мм | a, мм | h1, мм | b1, мм | h2, мм |
| 6 | 72 | 12 | 72 | 36 | 48 | 16 | 32 | 10 |
 рис. 1
рис. 1
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
Задача №2
Вычислить главные центральные моменты инерции составных сечений (рис.1). При расчете воспользоваться данными таблицы. Геометрические характеристики стали горячекатаной выбрать по ГОСТ 8239-89 (балки двутавровые) и ГОСТ 8240-89 (швеллеры).
| Вариант | № швеллера | № двутавра | a, мм | c, мм |
| 6 | 20 | 20 | 8 | 10 |
 рис.2
рис.2
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
Практическая работа №12
Геометрические характеристики плоских сечений
Задача№1
Вычислить главные центральные моменты инерции сечения, представленного на схеме (рис.1). При расчетах воспользоваться данными таблицы.
| Вариант | d1, мм | d2, мм | h, мм | b, мм | a, мм | h1, мм | b1, мм | h2, мм |
| 7 | 76 | 14 | 76 | 42 | 48 | 18 | 36 | 6 |
 рис. 1
рис. 1
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Задача №2
Вычислить главные центральные моменты инерции составных сечений (рис.1). При расчете воспользоваться данными таблицы. Геометрические характеристики стали горячекатаной выбрать по ГОСТ 8239-89 (балки двутавровые) и ГОСТ 8240-89 (швеллеры).
| Вариант | № швеллера | № двутавра | a, мм | c, мм |
| 7 | 22 | 22 | 10 | 15 |
 рис.2
рис.2
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
Практическая работа №12
Геометрические характеристики плоских сечений
Задача№1
Вычислить главные центральные моменты инерции сечения, представленного на схеме (рис.1). При расчетах воспользоваться данными таблицы.
| Вариант | d1, мм | d2, мм | h, мм | b, мм | a, мм | h1, мм | b1, мм | h2, мм |
| 8 | 88 | 16 | 88 | 48 | 56 | 20 | 40 | 8 |
 рис. 1
рис. 1
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Задача №2
Вычислить главные центральные моменты инерции составных сечений (рис.1). При расчете воспользоваться данными таблицы. Геометрические характеристики стали горячекатаной выбрать по ГОСТ 8239-89 (балки двутавровые) и ГОСТ 8240-89 (швеллеры).
| Вариант | № швеллера | № двутавра | a, мм | c, мм |
| 8 | 24 | 24 | 12 | 20 |
 рис.2
рис.2
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
Практическая работа №12
Геометрические характеристики плоских сечений
Задача№1
Вычислить главные центральные моменты инерции сечения, представленного на схеме (рис.1). При расчетах воспользоваться данными таблицы.
| Вариант | d1, мм | d2, мм | h, мм | b, мм | a, мм | h1, мм | b1, мм | h2, мм |
| 9 | 96 | 18 | 96 | 4 | 60 | 22 | 44 | 10 |
 рис. 1
рис. 1
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Задача №2
Вычислить главные центральные моменты инерции составных сечений (рис.1). При расчете воспользоваться данными таблицы. Геометрические характеристики стали горячекатаной выбрать по ГОСТ 8239-89 (балки двутавровые) и ГОСТ 8240-89 (швеллеры).
| Вариант | № швеллера | № двутавра | a, мм | c, мм |
| 9 | 27 | 27 | 14 | 25 |
 рис.2
рис.2
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
Практическая работа №12
Геометрические характеристики плоских сечений
Задача№1
Вычислить главные центральные моменты инерции сечения, представленного на схеме (рис.1). При расчетах воспользоваться данными таблицы.
| Вариант | d1, мм | d2, мм | h, мм | b, мм | a, мм | h1, мм | b1, мм | h2, мм |
| 10 | 104 | 20 | 104 | 60 | 64 | 24 | 48 | 6 |
 рис. 1
рис. 1
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Задача №2
Вычислить главные центральные моменты инерции составных сечений (рис.1). При расчете воспользоваться данными таблицы. Геометрические характеристики стали горячекатаной выбрать по ГОСТ 8239-89 (балки двутавровые) и ГОСТ 8240-89 (швеллеры).
| Вариант | № швеллера | № двутавра | a, мм | c, мм |
| 10 | 30 | 30 | 16 | 30 |
 рис.2
рис.2
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
Практическая работа №12
Геометрические характеристики плоских сечений
Задача№1
Вычислить главные центральные моменты инерции сечения, представленного на схеме (рис.1). При расчетах воспользоваться данными таблицы.
| Вариант | d1, мм | d2, мм | h, мм | b, мм | a, мм | h1, мм | b1, мм | h2, мм |
| 11 | 80 | 14 | 80 | 42 | 52 | 18 | 36 | 8 |
 рис. 1
рис. 1
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Задача №2
Вычислить главные центральные моменты инерции составных сечений (рис.1). При расчете воспользоваться данными таблицы. Геометрические характеристики стали горячекатаной выбрать по ГОСТ 8239-89 (балки двутавровые) и ГОСТ 8240-89 (швеллеры).
| Вариант | № швеллера | № двутавра | a, мм | c, мм |
| 11 | 10 | 10 | 8 | 10 |
 рис.2
рис.2
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
Практическая работа №12
Геометрические характеристики плоских сечений
Задача№1
Вычислить главные центральные моменты инерции сечения, представленного на схеме (рис.1). При расчетах воспользоваться данными таблицы.
| Вариант | d1, мм | d2, мм | h, мм | b, мм | a, мм | h1, мм | b1, мм | h2, мм |
| 12 | 88 | 16 | 88 | 48 | 56 | 20 | 40 | 10 |
 рис. 1
рис. 1
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
Задача №2
Вычислить главные центральные моменты инерции составных сечений (рис.1). При расчете воспользоваться данными таблицы. Геометрические характеристики стали горячекатаной выбрать по ГОСТ 8239-89 (балки двутавровые) и ГОСТ 8240-89 (швеллеры).
| Вариант | № швеллера | № двутавра | a, мм | c, мм |
| 12 | 12 | 12 | 10 | 15 |
 рис.2
рис.2
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
Практическая работа №12
Геометрические характеристики плоских сечений
Задача№1
Вычислить главные центральные моменты инерции сечения, представленного на схеме (рис.1). При расчетах воспользоваться данными таблицы.
| Вариант | d1, мм | d2, мм | h, мм | b, мм | a, мм | h1, мм | b1, мм | h2, мм |
| 13 | 96 | 18 | 96 | 54 | 60 | 22 | 44 | 6 |
 рис. 1
рис. 1
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Задача №2
Вычислить главные центральные моменты инерции составных сечений (рис.1). При расчете воспользоваться данными таблицы. Геометрические характеристики стали горячекатаной выбрать по ГОСТ 8239-89 (балки двутавровые) и ГОСТ 8240-89 (швеллеры).
| Вариант | № швеллера | № двутавра | a, мм | c, мм |
| 13 | 14 | 14 | 12 | 20 |
 рис.2
рис.2
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
Практическая работа №12
Геометрические характеристики плоских сечений
Задача№1
Вычислить главные центральные моменты инерции сечения, представленного на схеме (рис.1). При расчетах воспользоваться данными таблицы.
| Вариант | d1, мм | d2, мм | h, мм | b, мм | a, мм | h1, мм | b1, мм | h2, мм |
| 14 | 98 | 10 | 98 | 60 | 58 | 24 | 48 | 8 |
 рис. 1
рис. 1
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Задача №2
Вычислить главные центральные моменты инерции составных сечений (рис.1). При расчете воспользоваться данными таблицы. Геометрические характеристики стали горячекатаной выбрать по ГОСТ 8239-89 (балки двутавровые) и ГОСТ 8240-89 (швеллеры).
| Вариант | № швеллера | № двутавра | a, мм | c, мм |
| 14 | 16 | 16 | 14 | 25 |
 рис.2
рис.2
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
Практическая работа №12
Геометрические характеристики плоских сечений
Задача№1
Вычислить главные центральные моменты инерции сечения, представленного на схеме (рис.1). При расчетах воспользоваться данными таблицы.
| Вариант | d1, мм | d2, мм | h, мм | b, мм | a, мм | h1, мм | b1, мм | h2, мм |
| 15 | 72 | 12 | 72 | 36 | 48 | 16 | 32 | 10 |
 рис. 1
рис. 1
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Задача №2
Вычислить главные центральные моменты инерции составных сечений (рис.1). При расчете воспользоваться данными таблицы. Геометрические характеристики стали горячекатаной выбрать по ГОСТ 8239-89 (балки двутавровые) и ГОСТ 8240-89 (швеллеры).
| Вариант | № швеллера | № двутавра | a, мм | c, мм |
| 15 | 18 | 18 | 16 | 30 |
 рис.2
рис.2
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
Практическая работа №12
Геометрические характеристики плоских сечений
Задача№1
Вычислить главные центральные моменты инерции сечения, представленного на схеме (рис.1). При расчетах воспользоваться данными таблицы.
| Вариант | d1, мм | d2, мм | h, мм | b, мм | a, мм | h1, мм | b1, мм | h2, мм |
| 16 | 76 | 14 | 76 | 42 | 48 | 18 | 36 | 6 |
 рис. 1
рис. 1
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Задача №2
Вычислить главные центральные моменты инерции составных сечений (рис.1). При расчете воспользоваться данными таблицы. Геометрические характеристики стали горячекатаной выбрать по ГОСТ 8239-89 (балки двутавровые) и ГОСТ 8240-89 (швеллеры).
| Вариант | № швеллера | № двутавра | a, мм | c, мм |
| 16 | 20 | 20 | 8 | 10 |
 рис.2
рис.2
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
Практическая работа №12
Геометрические характеристики плоских сечений
Задача№1
Вычислить главные центральные моменты инерции сечения, представленного на схеме (рис.1). При расчетах воспользоваться данными таблицы.
| Вариант | d1, мм | d2, мм | h, мм | b, мм | a, мм | h1, мм | b1, мм | h2, мм |
| 17 | 88 | 16 | 88 | 48 | 56 | 20 | 40 | 8 |
 рис. 1
рис. 1
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Задача №2
Вычислить главные центральные моменты инерции составных сечений (рис.1). При расчете воспользоваться данными таблицы. Геометрические характеристики стали горячекатаной выбрать по ГОСТ 8239-89 (балки двутавровые) и ГОСТ 8240-89 (швеллеры).
| Вариант | № швеллера | № двутавра | a, мм | c, мм |
| 17 | 22 | 22 | 10 | 15 |
 рис.2
рис.2
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
Практическая работа №12
Геометрические характеристики плоских сечений
Задача№1
Вычислить главные центральные моменты инерции сечения, представленного на схеме (рис.1). При расчетах воспользоваться данными таблицы.
| Вариант | d1, мм | d2, мм | h, мм | b, мм | a, мм | h1, мм | b1, мм | h2, мм |
| 18 | 96 | 18 | 96 | 4 | 60 | 22 | 44 | 10 |
 рис. 1
рис. 1
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
Задача №2
Вычислить главные центральные моменты инерции составных сечений (рис.1). При расчете воспользоваться данными таблицы. Геометрические характеристики стали горячекатаной выбрать по ГОСТ 8239-89 (балки двутавровые) и ГОСТ 8240-89 (швеллеры).
| Вариант | № швеллера | № двутавра | a, мм | c, мм |
| 18 | 24 | 24 | 12 | 20 |
 рис.2
рис.2
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
Практическая работа №12
Геометрические характеристики плоских сечений
Задача№1
Вычислить главные центральные моменты инерции сечения, представленного на схеме (рис.1). При расчетах воспользоваться данными таблицы.
| Вариант | d1, мм | d2, мм | h, мм | b, мм | a, мм | h1, мм | b1, мм | h2, мм |
| 19 | 104 | 20 | 104 | 60 | 64 | 24 | 48 | 6 |
 рис. 1
рис. 1
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Задача №2
Вычислить главные центральные моменты инерции составных сечений (рис.1). При расчете воспользоваться данными таблицы. Геометрические характеристики стали горячекатаной выбрать по ГОСТ 8239-89 (балки двутавровые) и ГОСТ 8240-89 (швеллеры).
| Вариант | № швеллера | № двутавра | a, мм | c, мм |
| 19 | 27 | 27 | 14 | 25 |
 рис.2
рис.2
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
Практическая работа №12
Геометрические характеристики плоских сечений
Задача№1
Вычислить главные центральные моменты инерции сечения, представленного на схеме (рис.1). При расчетах воспользоваться данными таблицы.
| Вариант | d1, мм | d2, мм | h, мм | b, мм | a, мм | h1, мм | b1, мм | h2, мм |
| 20 | 88 | 16 | 88 | 48 | 56 | 20 | 40 | 10 |
 рис. 1
рис. 1
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Задача №2
Вычислить главные центральные моменты инерции составных сечений (рис.1). При расчете воспользоваться данными таблицы. Геометрические характеристики стали горячекатаной выбрать по ГОСТ 8239-89 (балки двутавровые) и ГОСТ 8240-89 (швеллеры).
| Вариант | № швеллера | № двутавра | a, мм | c, мм |
| 20 | 30 | 30 | 16 | 30 |
 рис.2
рис.2
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
Практическая работа №12
Геометрические характеристики плоских сечений
Задача№1
Вычислить главные центральные моменты инерции сечения, представленного на схеме (рис.1). При расчетах воспользоваться данными таблицы.
| Вариант | d1, мм | d2, мм | h, мм | b, мм | a, мм | h1, мм | b1, мм | h2, мм |
| 21 | 72 | 12 | 72 | 36 | 48 | 16 | 32 | 10 |
 рис. 1
рис. 1
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Задача №2
Вычислить главные центральные моменты инерции составных сечений (рис.1). При расчете воспользоваться данными таблицы. Геометрические характеристики стали горячекатаной выбрать по ГОСТ 8239-89 (балки двутавровые) и ГОСТ 8240-89 (швеллеры).
| Вариант | № швеллера | № двутавра | a, мм | c, мм |
| 21 | 10 | 10 | 8 | 10 |
 рис.2
рис.2
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
Практическая работа №12
Геометрические характеристики плоских сечений
Задача№1
Вычислить главные центральные моменты инерции сечения, представленного на схеме (рис.1). При расчетах воспользоваться данными таблицы.
| Вариант | d1, мм | d2, мм | h, мм | b, мм | a, мм | h1, мм | b1, мм | h2, мм |
| 22 | 76 | 14 | 76 | 42 | 48 | 18 | 36 | 6 |
 рис. 1
рис. 1
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Задача №2
Вычислить главные центральные моменты инерции составных сечений (рис.1). При расчете воспользоваться данными таблицы. Геометрические характеристики стали горячекатаной выбрать по ГОСТ 8239-89 (балки двутавровые) и ГОСТ 8240-89 (швеллеры).
| Вариант | № швеллера | № двутавра | a, мм | c, мм |
| 22 | 12 | 12 | 10 | 15 |
 рис.2
рис.2
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
Практическая работа №12
Геометрические характеристики плоских сечений
Задача№1
Вычислить главные центральные моменты инерции сечения, представленного на схеме (рис.1). При расчетах воспользоваться данными таблицы.
| Вариант | d1, мм | d2, мм | h, мм | b, мм | a, мм | h1, мм | b1, мм | h2, мм |
| 23 | 88 | 16 | 88 | 48 | 56 | 20 | 40 | 8 |
 рис. 1
рис. 1
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Задача №2
Вычислить главные центральные моменты инерции составных сечений (рис.1). При расчете воспользоваться данными таблицы. Геометрические характеристики стали горячекатаной выбрать по ГОСТ 8239-89 (балки двутавровые) и ГОСТ 8240-89 (швеллеры).
| Вариант | № швеллера | № двутавра | a, мм | c, мм |
| 23 | 14 | 14 | 12 | 20 |
 рис.2
рис.2
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
Практическая работа №12
Геометрические характеристики плоских сечений
Задача№1
Вычислить главные центральные моменты инерции сечения, представленного на схеме (рис.1). При расчетах воспользоваться данными таблицы.
| Вариант | d1, мм | d2, мм | h, мм | b, мм | a, мм | h1, мм | b1, мм | h2, мм |
| 24 | 96 | 18 | 96 | 4 | 60 | 22 | 44 | 10 |
 рис. 1
рис. 1
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
Задача №2
Вычислить главные центральные моменты инерции составных сечений (рис.1). При расчете воспользоваться данными таблицы. Геометрические характеристики стали горячекатаной выбрать по ГОСТ 8239-89 (балки двутавровые) и ГОСТ 8240-89 (швеллеры).
| Вариант | № швеллера | № двутавра | a, мм | c, мм |
| 24 | 18 | 18 | 16 | 30 |
 рис.2
рис.2
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
Практическая работа №12
Геометрические характеристики плоских сечений
Задача№1
Вычислить главные центральные моменты инерции сечения, представленного на схеме (рис.1). При расчетах воспользоваться данными таблицы.
| Вариант | d1, мм | d2, мм | h, мм | b, мм | a, мм | h1, мм | b1, мм | h2, мм |
| 25 | 72 | 12 | 72 | 36 | 48 | 16 | 32 | 6 |
 рис. 1
рис. 1
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Задача №2
Вычислить главные центральные моменты инерции составных сечений (рис.1). При расчете воспользоваться данными таблицы. Геометрические характеристики стали горячекатаной выбрать по ГОСТ 8239-89 (балки двутавровые) и ГОСТ 8240-89 (швеллеры).
| Вариант | № швеллера | № двутавра | a, мм | c, мм |
| 25 | 24 | 24 | 12 | 20 |
 рис.2
рис.2
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________










Просмотр содержимого документа
«Практическая работа №13»
Практическая работа №13
Кручение. Расчеты на прочность и жесткость при кручении
Задача
Для стального вала (рис. 1) круглого поперечного сечения определить значения внешних моментов, соответствующих передаваемым мощностям, и уравновешенный момент.
Построить эпюру крутящих моментов по длине вала.
Рациональным расположением шкивов на валу добиться уменьшения значения максимального крутящего момента на валу.
Построить эпюру крутящих моментов для этого случая.
Дальнейшие расчеты вести для вала с рациональным расположением шкивов.
Определить диаметры вала по сечениям из расчетов на прочность и жесткость. Полученный больший результат округлить до ближайшего четного и оканчивающегося на 5 числа.
При расчете использовать следующие данные: вал вращается с угловой скоростью  =25 рад/с; материал вала – сталь, допускаемое напряжение кручения 30 МПа.
=25 рад/с; материал вала – сталь, допускаемое напряжение кручения 30 МПа.
| Вариант | a=b=с, м | P1, кВт | P2, кВт | P3, кВт |
| 1 | 1,1 | 2,1 | 2,6 | 3,1 |
 рис. 1
рис. 1
Решение
Определить значения внешних моментов, соответствующих передаваемым мощностям, и уравновешенный момент
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
Построить эпюру крутящих моментов по длине вала


____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Построить эпюру крутящих моментов при рациональном расположении шкивов на валу


____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Определить диаметры вала по сечениям из расчетов на прочность и жесткость
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Практическая работа №13
Кручение. Расчеты на прочность и жесткость при кручении
Задача
Для стального вала (рис. 1) круглого поперечного сечения определить значения внешних моментов, соответствующих передаваемым мощностям, и уравновешенный момент.
Построить эпюру крутящих моментов по длине вала.
Рациональным расположением шкивов на валу добиться уменьшения значения максимального крутящего момента на валу.
Построить эпюру крутящих моментов для этого случая.
Дальнейшие расчеты вести для вала с рациональным расположением шкивов.
Определить диаметры вала по сечениям из расчетов на прочность и жесткость. Полученный больший результат округлить до ближайшего четного и оканчивающегося на 5 числа.
При расчете использовать следующие данные: вал вращается с угловой скоростью  =25 рад/с; материал вала – сталь, допускаемое напряжение кручения 30 МПа.
=25 рад/с; материал вала – сталь, допускаемое напряжение кручения 30 МПа.
| Вариант | a=b=с, м | P1, кВт | P2, кВт | P3, кВт |
| 2 | 1,2 | 2,2 | 2,7 | 3,2 |
 рис. 1
рис. 1
Решение
Определить значения внешних моментов, соответствующих передаваемым мощностям, и уравновешенный момент
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
Построить эпюру крутящих моментов по длине вала


____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Построить эпюру крутящих моментов при рациональном расположении шкивов на валу


____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Определить диаметры вала по сечениям из расчетов на прочность и жесткость
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Практическая работа №13
Кручение. Расчеты на прочность и жесткость при кручении
Задача
Для стального вала (рис. 1) круглого поперечного сечения определить значения внешних моментов, соответствующих передаваемым мощностям, и уравновешенный момент.
Построить эпюру крутящих моментов по длине вала.
Рациональным расположением шкивов на валу добиться уменьшения значения максимального крутящего момента на валу.
Построить эпюру крутящих моментов для этого случая.
Дальнейшие расчеты вести для вала с рациональным расположением шкивов.
Определить диаметры вала по сечениям из расчетов на прочность и жесткость. Полученный больший результат округлить до ближайшего четного и оканчивающегося на 5 числа.
При расчете использовать следующие данные: вал вращается с угловой скоростью  =25 рад/с; материал вала – сталь, допускаемое напряжение кручения 30 МПа.
=25 рад/с; материал вала – сталь, допускаемое напряжение кручения 30 МПа.
| Вариант | a=b=с, м | P1, кВт | P2, кВт | P3, кВт |
| 3 | 1,3 | 2,3 | 2,8 | 3,3 |
 рис. 1
рис. 1
Решение
Определить значения внешних моментов, соответствующих передаваемым мощностям, и уравновешенный момент
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
Построить эпюру крутящих моментов по длине вала


____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Построить эпюру крутящих моментов при рациональном расположении шкивов на валу


____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Определить диаметры вала по сечениям из расчетов на прочность и жесткость
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Практическая работа №13
Кручение. Расчеты на прочность и жесткость при кручении
Задача
Для стального вала (рис. 1) круглого поперечного сечения определить значения внешних моментов, соответствующих передаваемым мощностям, и уравновешенный момент.
Построить эпюру крутящих моментов по длине вала.
Рациональным расположением шкивов на валу добиться уменьшения значения максимального крутящего момента на валу.
Построить эпюру крутящих моментов для этого случая.
Дальнейшие расчеты вести для вала с рациональным расположением шкивов.
Определить диаметры вала по сечениям из расчетов на прочность и жесткость. Полученный больший результат округлить до ближайшего четного и оканчивающегося на 5 числа.
При расчете использовать следующие данные: вал вращается с угловой скоростью  =25 рад/с; материал вала – сталь, допускаемое напряжение кручения 30 МПа.
=25 рад/с; материал вала – сталь, допускаемое напряжение кручения 30 МПа.
| Вариант | a=b=с, м | P1, кВт | P2, кВт | P3, кВт |
| 4 | 1,4 | 2,4 | 2,9 | 3,4 |
 рис. 1
рис. 1
Решение
Определить значения внешних моментов, соответствующих передаваемым мощностям, и уравновешенный момент
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
Построить эпюру крутящих моментов по длине вала


____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Построить эпюру крутящих моментов при рациональном расположении шкивов на валу


____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Определить диаметры вала по сечениям из расчетов на прочность и жесткость
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Практическая работа №13
Кручение. Расчеты на прочность и жесткость при кручении
Задача
Для стального вала (рис. 1) круглого поперечного сечения определить значения внешних моментов, соответствующих передаваемым мощностям, и уравновешенный момент.
Построить эпюру крутящих моментов по длине вала.
Рациональным расположением шкивов на валу добиться уменьшения значения максимального крутящего момента на валу.
Построить эпюру крутящих моментов для этого случая.
Дальнейшие расчеты вести для вала с рациональным расположением шкивов.
Определить диаметры вала по сечениям из расчетов на прочность и жесткость. Полученный больший результат округлить до ближайшего четного и оканчивающегося на 5 числа.
При расчете использовать следующие данные: вал вращается с угловой скоростью  =25 рад/с; материал вала – сталь, допускаемое напряжение кручения 30 МПа.
=25 рад/с; материал вала – сталь, допускаемое напряжение кручения 30 МПа.
| Вариант | a=b=с, м | P1, кВт | P2, кВт | P3, кВт |
| 5 | 1,5 | 2,5 | 3,0 | 3,5 |
 рис. 1
рис. 1
Решение
Определить значения внешних моментов, соответствующих передаваемым мощностям, и уравновешенный момент
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
Построить эпюру крутящих моментов по длине вала


____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Построить эпюру крутящих моментов при рациональном расположении шкивов на валу


____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Определить диаметры вала по сечениям из расчетов на прочность и жесткость
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Практическая работа №13
Кручение. Расчеты на прочность и жесткость при кручении
Задача
Для стального вала (рис. 1) круглого поперечного сечения определить значения внешних моментов, соответствующих передаваемым мощностям, и уравновешенный момент.
Построить эпюру крутящих моментов по длине вала.
Рациональным расположением шкивов на валу добиться уменьшения значения максимального крутящего момента на валу.
Построить эпюру крутящих моментов для этого случая.
Дальнейшие расчеты вести для вала с рациональным расположением шкивов.
Определить диаметры вала по сечениям из расчетов на прочность и жесткость. Полученный больший результат округлить до ближайшего четного и оканчивающегося на 5 числа.
При расчете использовать следующие данные: вал вращается с угловой скоростью  =25 рад/с; материал вала – сталь, допускаемое напряжение кручения 30 МПа.
=25 рад/с; материал вала – сталь, допускаемое напряжение кручения 30 МПа.
| Вариант | a=b=с, м | P1, кВт | P2, кВт | P3, кВт |
| 6 | 1,6 | 2,6 | 3,1 | 3,6 |
 рис. 1
рис. 1
Решение
Определить значения внешних моментов, соответствующих передаваемым мощностям, и уравновешенный момент
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
Построить эпюру крутящих моментов по длине вала


____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Построить эпюру крутящих моментов при рациональном расположении шкивов на валу


____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Определить диаметры вала по сечениям из расчетов на прочность и жесткость
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Практическая работа №13
Кручение. Расчеты на прочность и жесткость при кручении
Задача
Для стального вала (рис. 1) круглого поперечного сечения определить значения внешних моментов, соответствующих передаваемым мощностям, и уравновешенный момент.
Построить эпюру крутящих моментов по длине вала.
Рациональным расположением шкивов на валу добиться уменьшения значения максимального крутящего момента на валу.
Построить эпюру крутящих моментов для этого случая.
Дальнейшие расчеты вести для вала с рациональным расположением шкивов.
Определить диаметры вала по сечениям из расчетов на прочность и жесткость. Полученный больший результат округлить до ближайшего четного и оканчивающегося на 5 числа.
При расчете использовать следующие данные: вал вращается с угловой скоростью  =25 рад/с; материал вала – сталь, допускаемое напряжение кручения 30 МПа.
=25 рад/с; материал вала – сталь, допускаемое напряжение кручения 30 МПа.
| Вариант | a=b=с, м | P1, кВт | P2, кВт | P3, кВт |
| 7 | 1,7 | 2,7 | 3,2 | 3,7 |
 рис. 1
рис. 1
Решение
Определить значения внешних моментов, соответствующих передаваемым мощностям, и уравновешенный момент
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
Построить эпюру крутящих моментов по длине вала


____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Построить эпюру крутящих моментов при рациональном расположении шкивов на валу


____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Определить диаметры вала по сечениям из расчетов на прочность и жесткость
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Практическая работа №13
Кручение. Расчеты на прочность и жесткость при кручении
Задача
Для стального вала (рис. 1) круглого поперечного сечения определить значения внешних моментов, соответствующих передаваемым мощностям, и уравновешенный момент.
Построить эпюру крутящих моментов по длине вала.
Рациональным расположением шкивов на валу добиться уменьшения значения максимального крутящего момента на валу.
Построить эпюру крутящих моментов для этого случая.
Дальнейшие расчеты вести для вала с рациональным расположением шкивов.
Определить диаметры вала по сечениям из расчетов на прочность и жесткость. Полученный больший результат округлить до ближайшего четного и оканчивающегося на 5 числа.
При расчете использовать следующие данные: вал вращается с угловой скоростью  =25 рад/с; материал вала – сталь, допускаемое напряжение кручения 30 МПа.
=25 рад/с; материал вала – сталь, допускаемое напряжение кручения 30 МПа.
| Вариант | a=b=с, м | P1, кВт | P2, кВт | P3, кВт |
| 8 | 1,8 | 2,8 | 3,3 | 3,8 |
 рис. 1
рис. 1
Решение
Определить значения внешних моментов, соответствующих передаваемым мощностям, и уравновешенный момент
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
Построить эпюру крутящих моментов по длине вала


____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Построить эпюру крутящих моментов при рациональном расположении шкивов на валу


____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Определить диаметры вала по сечениям из расчетов на прочность и жесткость
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Практическая работа №13
Кручение. Расчеты на прочность и жесткость при кручении
Задача
Для стального вала (рис. 1) круглого поперечного сечения определить значения внешних моментов, соответствующих передаваемым мощностям, и уравновешенный момент.
Построить эпюру крутящих моментов по длине вала.
Рациональным расположением шкивов на валу добиться уменьшения значения максимального крутящего момента на валу.
Построить эпюру крутящих моментов для этого случая.
Дальнейшие расчеты вести для вала с рациональным расположением шкивов.
Определить диаметры вала по сечениям из расчетов на прочность и жесткость. Полученный больший результат округлить до ближайшего четного и оканчивающегося на 5 числа.
При расчете использовать следующие данные: вал вращается с угловой скоростью  =25 рад/с; материал вала – сталь, допускаемое напряжение кручения 30 МПа.
=25 рад/с; материал вала – сталь, допускаемое напряжение кручения 30 МПа.
| Вариант | a=b=с, м | P1, кВт | P2, кВт | P3, кВт |
| 9 | 1,9 | 2,9 | 3,4 | 3,9 |
 рис. 1
рис. 1
Решение
Определить значения внешних моментов, соответствующих передаваемым мощностям, и уравновешенный момент
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
Построить эпюру крутящих моментов по длине вала


____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Построить эпюру крутящих моментов при рациональном расположении шкивов на валу


____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Определить диаметры вала по сечениям из расчетов на прочность и жесткость
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Практическая работа №13
Кручение. Расчеты на прочность и жесткость при кручении
Задача
Для стального вала (рис. 1) круглого поперечного сечения определить значения внешних моментов, соответствующих передаваемым мощностям, и уравновешенный момент.
Построить эпюру крутящих моментов по длине вала.
Рациональным расположением шкивов на валу добиться уменьшения значения максимального крутящего момента на валу.
Построить эпюру крутящих моментов для этого случая.
Дальнейшие расчеты вести для вала с рациональным расположением шкивов.
Определить диаметры вала по сечениям из расчетов на прочность и жесткость. Полученный больший результат округлить до ближайшего четного и оканчивающегося на 5 числа.
При расчете использовать следующие данные: вал вращается с угловой скоростью  =25 рад/с; материал вала – сталь, допускаемое напряжение кручения 30 МПа.
=25 рад/с; материал вала – сталь, допускаемое напряжение кручения 30 МПа.
| Вариант | a=b=с, м | P1, кВт | P2, кВт | P3, кВт |
| 10 | 2,0 | 3,0 | 3,5 | 4,0 |
 рис. 1
рис. 1
Решение
Определить значения внешних моментов, соответствующих передаваемым мощностям, и уравновешенный момент
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
Построить эпюру крутящих моментов по длине вала


____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Построить эпюру крутящих моментов при рациональном расположении шкивов на валу


____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Определить диаметры вала по сечениям из расчетов на прочность и жесткость
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Практическая работа №13
Кручение. Расчеты на прочность и жесткость при кручении
Задача
Для стального вала (рис. 1) круглого поперечного сечения определить значения внешних моментов, соответствующих передаваемым мощностям, и уравновешенный момент.
Построить эпюру крутящих моментов по длине вала.
Рациональным расположением шкивов на валу добиться уменьшения значения максимального крутящего момента на валу.
Построить эпюру крутящих моментов для этого случая.
Дальнейшие расчеты вести для вала с рациональным расположением шкивов.
Определить диаметры вала по сечениям из расчетов на прочность и жесткость. Полученный больший результат округлить до ближайшего четного и оканчивающегося на 5 числа.
При расчете использовать следующие данные: вал вращается с угловой скоростью  =25 рад/с; материал вала – сталь, допускаемое напряжение кручения 30 МПа.
=25 рад/с; материал вала – сталь, допускаемое напряжение кручения 30 МПа.
| Вариант | a=b=с, м | P1, кВт | P2, кВт | P3, кВт |
| 11 | 2,1 | 3,2 | 3,6 | 4,1 |
 рис. 1
рис. 1
Решение
Определить значения внешних моментов, соответствующих передаваемым мощностям, и уравновешенный момент
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
Построить эпюру крутящих моментов по длине вала


____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Построить эпюру крутящих моментов при рациональном расположении шкивов на валу


____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Определить диаметры вала по сечениям из расчетов на прочность и жесткость
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Практическая работа №13
Кручение. Расчеты на прочность и жесткость при кручении
Задача
Для стального вала (рис. 1) круглого поперечного сечения определить значения внешних моментов, соответствующих передаваемым мощностям, и уравновешенный момент.
Построить эпюру крутящих моментов по длине вала.
Рациональным расположением шкивов на валу добиться уменьшения значения максимального крутящего момента на валу.
Построить эпюру крутящих моментов для этого случая.
Дальнейшие расчеты вести для вала с рациональным расположением шкивов.
Определить диаметры вала по сечениям из расчетов на прочность и жесткость. Полученный больший результат округлить до ближайшего четного и оканчивающегося на 5 числа.
При расчете использовать следующие данные: вал вращается с угловой скоростью  =25 рад/с; материал вала – сталь, допускаемое напряжение кручения 30 МПа.
=25 рад/с; материал вала – сталь, допускаемое напряжение кручения 30 МПа.
| Вариант | a=b=с, м | P1, кВт | P2, кВт | P3, кВт |
| 12 | 2,2 | 3,3 | 3,7 | 4,2 |
 рис. 1
рис. 1
Решение
Определить значения внешних моментов, соответствующих передаваемым мощностям, и уравновешенный момент
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
Построить эпюру крутящих моментов по длине вала


____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Построить эпюру крутящих моментов при рациональном расположении шкивов на валу


____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Определить диаметры вала по сечениям из расчетов на прочность и жесткость
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Практическая работа №13
Кручение. Расчеты на прочность и жесткость при кручении
Задача
Для стального вала (рис. 1) круглого поперечного сечения определить значения внешних моментов, соответствующих передаваемым мощностям, и уравновешенный момент.
Построить эпюру крутящих моментов по длине вала.
Рациональным расположением шкивов на валу добиться уменьшения значения максимального крутящего момента на валу.
Построить эпюру крутящих моментов для этого случая.
Дальнейшие расчеты вести для вала с рациональным расположением шкивов.
Определить диаметры вала по сечениям из расчетов на прочность и жесткость. Полученный больший результат округлить до ближайшего четного и оканчивающегося на 5 числа.
При расчете использовать следующие данные: вал вращается с угловой скоростью  =25 рад/с; материал вала – сталь, допускаемое напряжение кручения 30 МПа.
=25 рад/с; материал вала – сталь, допускаемое напряжение кручения 30 МПа.
| Вариант | a=b=с, м | P1, кВт | P2, кВт | P3, кВт |
| 13 | 2,3 | 3,4 | 3,8 | 4,3 |
 рис. 1
рис. 1
Решение
Определить значения внешних моментов, соответствующих передаваемым мощностям, и уравновешенный момент
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
Построить эпюру крутящих моментов по длине вала


____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Построить эпюру крутящих моментов при рациональном расположении шкивов на валу


____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Определить диаметры вала по сечениям из расчетов на прочность и жесткость
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Практическая работа №13
Кручение. Расчеты на прочность и жесткость при кручении
Задача
Для стального вала (рис. 1) круглого поперечного сечения определить значения внешних моментов, соответствующих передаваемым мощностям, и уравновешенный момент.
Построить эпюру крутящих моментов по длине вала.
Рациональным расположением шкивов на валу добиться уменьшения значения максимального крутящего момента на валу.
Построить эпюру крутящих моментов для этого случая.
Дальнейшие расчеты вести для вала с рациональным расположением шкивов.
Определить диаметры вала по сечениям из расчетов на прочность и жесткость. Полученный больший результат округлить до ближайшего четного и оканчивающегося на 5 числа.
При расчете использовать следующие данные: вал вращается с угловой скоростью  =25 рад/с; материал вала – сталь, допускаемое напряжение кручения 30 МПа.
=25 рад/с; материал вала – сталь, допускаемое напряжение кручения 30 МПа.
| Вариант | a=b=с, м | P1, кВт | P2, кВт | P3, кВт |
| 14 | 2,4 | 3,5 | 3,9 | 4,4 |
 рис. 1
рис. 1
Решение
Определить значения внешних моментов, соответствующих передаваемым мощностям, и уравновешенный момент
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
Построить эпюру крутящих моментов по длине вала


____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Построить эпюру крутящих моментов при рациональном расположении шкивов на валу


____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Определить диаметры вала по сечениям из расчетов на прочность и жесткость
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Практическая работа №13
Кручение. Расчеты на прочность и жесткость при кручении
Задача
Для стального вала (рис. 1) круглого поперечного сечения определить значения внешних моментов, соответствующих передаваемым мощностям, и уравновешенный момент.
Построить эпюру крутящих моментов по длине вала.
Рациональным расположением шкивов на валу добиться уменьшения значения максимального крутящего момента на валу.
Построить эпюру крутящих моментов для этого случая.
Дальнейшие расчеты вести для вала с рациональным расположением шкивов.
Определить диаметры вала по сечениям из расчетов на прочность и жесткость. Полученный больший результат округлить до ближайшего четного и оканчивающегося на 5 числа.
При расчете использовать следующие данные: вал вращается с угловой скоростью  =25 рад/с; материал вала – сталь, допускаемое напряжение кручения 30 МПа.
=25 рад/с; материал вала – сталь, допускаемое напряжение кручения 30 МПа.
| Вариант | a=b=с, м | P1, кВт | P2, кВт | P3, кВт |
| 15 | 2,5 | 3,6 | 4,0 | 4,5 |
 рис. 1
рис. 1
Решение
Определить значения внешних моментов, соответствующих передаваемым мощностям, и уравновешенный момент
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
Построить эпюру крутящих моментов по длине вала


____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Построить эпюру крутящих моментов при рациональном расположении шкивов на валу


____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Определить диаметры вала по сечениям из расчетов на прочность и жесткость
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Практическая работа №13
Кручение. Расчеты на прочность и жесткость при кручении
Задача
Для стального вала (рис. 1) круглого поперечного сечения определить значения внешних моментов, соответствующих передаваемым мощностям, и уравновешенный момент.
Построить эпюру крутящих моментов по длине вала.
Рациональным расположением шкивов на валу добиться уменьшения значения максимального крутящего момента на валу.
Построить эпюру крутящих моментов для этого случая.
Дальнейшие расчеты вести для вала с рациональным расположением шкивов.
Определить диаметры вала по сечениям из расчетов на прочность и жесткость. Полученный больший результат округлить до ближайшего четного и оканчивающегося на 5 числа.
При расчете использовать следующие данные: вал вращается с угловой скоростью  =25 рад/с; материал вала – сталь, допускаемое напряжение кручения 30 МПа.
=25 рад/с; материал вала – сталь, допускаемое напряжение кручения 30 МПа.
| Вариант | a=b=с, м | P1, кВт | P2, кВт | P3, кВт |
| 16 | 2,6 | 3,7 | 4,1 | 4,6 |
 рис. 1
рис. 1
Решение
Определить значения внешних моментов, соответствующих передаваемым мощностям, и уравновешенный момент
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
Построить эпюру крутящих моментов по длине вала


____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Построить эпюру крутящих моментов при рациональном расположении шкивов на валу


____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Определить диаметры вала по сечениям из расчетов на прочность и жесткость
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Практическая работа №13
Кручение. Расчеты на прочность и жесткость при кручении
Задача
Для стального вала (рис. 1) круглого поперечного сечения определить значения внешних моментов, соответствующих передаваемым мощностям, и уравновешенный момент.
Построить эпюру крутящих моментов по длине вала.
Рациональным расположением шкивов на валу добиться уменьшения значения максимального крутящего момента на валу.
Построить эпюру крутящих моментов для этого случая.
Дальнейшие расчеты вести для вала с рациональным расположением шкивов.
Определить диаметры вала по сечениям из расчетов на прочность и жесткость. Полученный больший результат округлить до ближайшего четного и оканчивающегося на 5 числа.
При расчете использовать следующие данные: вал вращается с угловой скоростью  =25 рад/с; материал вала – сталь, допускаемое напряжение кручения 30 МПа.
=25 рад/с; материал вала – сталь, допускаемое напряжение кручения 30 МПа.
| Вариант | a=b=с, м | P1, кВт | P2, кВт | P3, кВт |
| 17 | 2,7 | 3,8 | 4,2 | 4,7 |
 рис. 1
рис. 1
Решение
Определить значения внешних моментов, соответствующих передаваемым мощностям, и уравновешенный момент
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
Построить эпюру крутящих моментов по длине вала


____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Построить эпюру крутящих моментов при рациональном расположении шкивов на валу


____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Определить диаметры вала по сечениям из расчетов на прочность и жесткость
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Практическая работа №13
Кручение. Расчеты на прочность и жесткость при кручении
Задача
Для стального вала (рис. 1) круглого поперечного сечения определить значения внешних моментов, соответствующих передаваемым мощностям, и уравновешенный момент.
Построить эпюру крутящих моментов по длине вала.
Рациональным расположением шкивов на валу добиться уменьшения значения максимального крутящего момента на валу.
Построить эпюру крутящих моментов для этого случая.
Дальнейшие расчеты вести для вала с рациональным расположением шкивов.
Определить диаметры вала по сечениям из расчетов на прочность и жесткость. Полученный больший результат округлить до ближайшего четного и оканчивающегося на 5 числа.
При расчете использовать следующие данные: вал вращается с угловой скоростью  =25 рад/с; материал вала – сталь, допускаемое напряжение кручения 30 МПа.
=25 рад/с; материал вала – сталь, допускаемое напряжение кручения 30 МПа.
| Вариант | a=b=с, м | P1, кВт | P2, кВт | P3, кВт |
| 18 | 2,8 | 3,9 | 4,3 | 4,8 |
 рис. 1
рис. 1
Решение
Определить значения внешних моментов, соответствующих передаваемым мощностям, и уравновешенный момент
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
Построить эпюру крутящих моментов по длине вала


____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Построить эпюру крутящих моментов при рациональном расположении шкивов на валу


____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Определить диаметры вала по сечениям из расчетов на прочность и жесткость
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Практическая работа №13
Кручение. Расчеты на прочность и жесткость при кручении
Задача
Для стального вала (рис. 1) круглого поперечного сечения определить значения внешних моментов, соответствующих передаваемым мощностям, и уравновешенный момент.
Построить эпюру крутящих моментов по длине вала.
Рациональным расположением шкивов на валу добиться уменьшения значения максимального крутящего момента на валу.
Построить эпюру крутящих моментов для этого случая.
Дальнейшие расчеты вести для вала с рациональным расположением шкивов.
Определить диаметры вала по сечениям из расчетов на прочность и жесткость. Полученный больший результат округлить до ближайшего четного и оканчивающегося на 5 числа.
При расчете использовать следующие данные: вал вращается с угловой скоростью  =25 рад/с; материал вала – сталь, допускаемое напряжение кручения 30 МПа.
=25 рад/с; материал вала – сталь, допускаемое напряжение кручения 30 МПа.
| Вариант | a=b=с, м | P1, кВт | P2, кВт | P3, кВт |
| 19 | 2,9 | 4,0 | 4,4 | 4,9 |
 рис. 1
рис. 1
Решение
Определить значения внешних моментов, соответствующих передаваемым мощностям, и уравновешенный момент
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
Построить эпюру крутящих моментов по длине вала


____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Построить эпюру крутящих моментов при рациональном расположении шкивов на валу


____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Определить диаметры вала по сечениям из расчетов на прочность и жесткость
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Практическая работа №13
Кручение. Расчеты на прочность и жесткость при кручении
Задача
Для стального вала (рис. 1) круглого поперечного сечения определить значения внешних моментов, соответствующих передаваемым мощностям, и уравновешенный момент.
Построить эпюру крутящих моментов по длине вала.
Рациональным расположением шкивов на валу добиться уменьшения значения максимального крутящего момента на валу.
Построить эпюру крутящих моментов для этого случая.
Дальнейшие расчеты вести для вала с рациональным расположением шкивов.
Определить диаметры вала по сечениям из расчетов на прочность и жесткость. Полученный больший результат округлить до ближайшего четного и оканчивающегося на 5 числа.
При расчете использовать следующие данные: вал вращается с угловой скоростью  =25 рад/с; материал вала – сталь, допускаемое напряжение кручения 30 МПа.
=25 рад/с; материал вала – сталь, допускаемое напряжение кручения 30 МПа.
| Вариант | a=b=с, м | P1, кВт | P2, кВт | P3, кВт |
| 20 | 3,0 | 4,1 | 4,5 | 5,0 |
 рис. 1
рис. 1
Решение
Определить значения внешних моментов, соответствующих передаваемым мощностям, и уравновешенный момент
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
Построить эпюру крутящих моментов по длине вала


____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Построить эпюру крутящих моментов при рациональном расположении шкивов на валу


____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Определить диаметры вала по сечениям из расчетов на прочность и жесткость
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Практическая работа №13
Кручение. Расчеты на прочность и жесткость при кручении
Задача
Для стального вала (рис. 1) круглого поперечного сечения определить значения внешних моментов, соответствующих передаваемым мощностям, и уравновешенный момент.
Построить эпюру крутящих моментов по длине вала.
Рациональным расположением шкивов на валу добиться уменьшения значения максимального крутящего момента на валу.
Построить эпюру крутящих моментов для этого случая.
Дальнейшие расчеты вести для вала с рациональным расположением шкивов.
Определить диаметры вала по сечениям из расчетов на прочность и жесткость. Полученный больший результат округлить до ближайшего четного и оканчивающегося на 5 числа.
При расчете использовать следующие данные: вал вращается с угловой скоростью  =25 рад/с; материал вала – сталь, допускаемое напряжение кручения 30 МПа.
=25 рад/с; материал вала – сталь, допускаемое напряжение кручения 30 МПа.
| Вариант | a=b=с, м | P1, кВт | P2, кВт | P3, кВт |
| 21 | 3,1 | 4,2 | 4,6 | 5,1 |
 рис. 1
рис. 1
Решение
Определить значения внешних моментов, соответствующих передаваемым мощностям, и уравновешенный момент
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
Построить эпюру крутящих моментов по длине вала


____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Построить эпюру крутящих моментов при рациональном расположении шкивов на валу


____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Определить диаметры вала по сечениям из расчетов на прочность и жесткость
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Практическая работа №13
Кручение. Расчеты на прочность и жесткость при кручении
Задача
Для стального вала (рис. 1) круглого поперечного сечения определить значения внешних моментов, соответствующих передаваемым мощностям, и уравновешенный момент.
Построить эпюру крутящих моментов по длине вала.
Рациональным расположением шкивов на валу добиться уменьшения значения максимального крутящего момента на валу.
Построить эпюру крутящих моментов для этого случая.
Дальнейшие расчеты вести для вала с рациональным расположением шкивов.
Определить диаметры вала по сечениям из расчетов на прочность и жесткость. Полученный больший результат округлить до ближайшего четного и оканчивающегося на 5 числа.
При расчете использовать следующие данные: вал вращается с угловой скоростью  =25 рад/с; материал вала – сталь, допускаемое напряжение кручения 30 МПа.
=25 рад/с; материал вала – сталь, допускаемое напряжение кручения 30 МПа.
| Вариант | a=b=с, м | P1, кВт | P2, кВт | P3, кВт |
| 22 | 3,2 | 4,3 | 4,7 | 5,2 |
 рис. 1
рис. 1
Решение
Определить значения внешних моментов, соответствующих передаваемым мощностям, и уравновешенный момент
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
Построить эпюру крутящих моментов по длине вала


____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Построить эпюру крутящих моментов при рациональном расположении шкивов на валу


____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Определить диаметры вала по сечениям из расчетов на прочность и жесткость
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Практическая работа №13
Кручение. Расчеты на прочность и жесткость при кручении
Задача
Для стального вала (рис. 1) круглого поперечного сечения определить значения внешних моментов, соответствующих передаваемым мощностям, и уравновешенный момент.
Построить эпюру крутящих моментов по длине вала.
Рациональным расположением шкивов на валу добиться уменьшения значения максимального крутящего момента на валу.
Построить эпюру крутящих моментов для этого случая.
Дальнейшие расчеты вести для вала с рациональным расположением шкивов.
Определить диаметры вала по сечениям из расчетов на прочность и жесткость. Полученный больший результат округлить до ближайшего четного и оканчивающегося на 5 числа.
При расчете использовать следующие данные: вал вращается с угловой скоростью  =25 рад/с; материал вала – сталь, допускаемое напряжение кручения 30 МПа.
=25 рад/с; материал вала – сталь, допускаемое напряжение кручения 30 МПа.
| Вариант | a=b=с, м | P1, кВт | P2, кВт | P3, кВт |
| 23 | 3,3 | 4,4 | 4,8 | 5,3 |
 рис. 1
рис. 1
Решение
Определить значения внешних моментов, соответствующих передаваемым мощностям, и уравновешенный момент
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
Построить эпюру крутящих моментов по длине вала


____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Построить эпюру крутящих моментов при рациональном расположении шкивов на валу


____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Определить диаметры вала по сечениям из расчетов на прочность и жесткость
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Практическая работа №13
Кручение. Расчеты на прочность и жесткость при кручении
Задача
Для стального вала (рис. 1) круглого поперечного сечения определить значения внешних моментов, соответствующих передаваемым мощностям, и уравновешенный момент.
Построить эпюру крутящих моментов по длине вала.
Рациональным расположением шкивов на валу добиться уменьшения значения максимального крутящего момента на валу.
Построить эпюру крутящих моментов для этого случая.
Дальнейшие расчеты вести для вала с рациональным расположением шкивов.
Определить диаметры вала по сечениям из расчетов на прочность и жесткость. Полученный больший результат округлить до ближайшего четного и оканчивающегося на 5 числа.
При расчете использовать следующие данные: вал вращается с угловой скоростью  =25 рад/с; материал вала – сталь, допускаемое напряжение кручения 30 МПа.
=25 рад/с; материал вала – сталь, допускаемое напряжение кручения 30 МПа.
| Вариант | a=b=с, м | P1, кВт | P2, кВт | P3, кВт |
| 24 | 3,4 | 4,5 | 4,9 | 5,4 |
 рис. 1
рис. 1
Решение
Определить значения внешних моментов, соответствующих передаваемым мощностям, и уравновешенный момент
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
Построить эпюру крутящих моментов по длине вала


____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Построить эпюру крутящих моментов при рациональном расположении шкивов на валу


____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Определить диаметры вала по сечениям из расчетов на прочность и жесткость
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Практическая работа №13
Кручение. Расчеты на прочность и жесткость при кручении
Задача
Для стального вала (рис. 1) круглого поперечного сечения определить значения внешних моментов, соответствующих передаваемым мощностям, и уравновешенный момент.
Построить эпюру крутящих моментов по длине вала.
Рациональным расположением шкивов на валу добиться уменьшения значения максимального крутящего момента на валу.
Построить эпюру крутящих моментов для этого случая.
Дальнейшие расчеты вести для вала с рациональным расположением шкивов.
Определить диаметры вала по сечениям из расчетов на прочность и жесткость. Полученный больший результат округлить до ближайшего четного и оканчивающегося на 5 числа.
При расчете использовать следующие данные: вал вращается с угловой скоростью  =25 рад/с; материал вала – сталь, допускаемое напряжение кручения 30 МПа.
=25 рад/с; материал вала – сталь, допускаемое напряжение кручения 30 МПа.
| Вариант | a=b=с, м | P1, кВт | P2, кВт | P3, кВт |
| 25 | 3,5 | 4,6 | 5,0 | 5,5 |
 рис. 1
рис. 1
Решение
Определить значения внешних моментов, соответствующих передаваемым мощностям, и уравновешенный момент
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
Построить эпюру крутящих моментов по длине вала


____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Построить эпюру крутящих моментов при рациональном расположении шкивов на валу


____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Определить диаметры вала по сечениям из расчетов на прочность и жесткость
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Просмотр содержимого документа
«Практическая работа №14»
Практическая работа №14
Кручение стержня круглого сечения
Задача
Жестко защемленный одним концом стальной стержень круглого поперечного сечения скручивается четырьмя моментами  (рис. 1).
(рис. 1).
Требуется:
построить эпюру крутящих моментов;
при заданном допускаемом касательном напряжении
 из условия прочности определить диаметр вала, округлив его до ближайшего из следующих значений 30, 35, 40, 45, 50, 60, 70, 80, 90, 100, 200 мм.
из условия прочности определить диаметр вала, округлив его до ближайшего из следующих значений 30, 35, 40, 45, 50, 60, 70, 80, 90, 100, 200 мм.
| Вариант | M1, кН | M2, кН | M3, кН | M, кН |
| 1 | 1,0 | 2,0 | 1,0 | 1,0 |
 рис. 1
рис. 1
Решение
1. Определить реактивный момент, возникающий в жесткой заделке
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
Построить эпюру крутящих моментов по длине вала


____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

Определить диаметр вала из условия прочности
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Практическая работа №14
Кручение стержня круглого сечения
Задача
Жестко защемленный одним концом стальной стержень круглого поперечного сечения скручивается четырьмя моментами  (рис. 1).
(рис. 1).
Требуется:
построить эпюру крутящих моментов;
при заданном допускаемом касательном напряжении
 из условия прочности определить диаметр вала, округлив его до ближайшего из следующих значений 30, 35, 40, 45, 50, 60, 70, 80, 90, 100, 200 мм.
из условия прочности определить диаметр вала, округлив его до ближайшего из следующих значений 30, 35, 40, 45, 50, 60, 70, 80, 90, 100, 200 мм.
| Вариант | M1, кН | M2, кН | M3, кН | M, кН |
| 2 | 1,0 | 2,0 | 1,0 | 0,8 |
 рис. 1
рис. 1
Решение
1. Определить реактивный момент, возникающий в жесткой заделке
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
Построить эпюру крутящих моментов по длине вала


____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

Определить диаметр вала из условия прочности
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Практическая работа №14
Кручение стержня круглого сечения
Задача
Жестко защемленный одним концом стальной стержень круглого поперечного сечения скручивается четырьмя моментами  (рис. 1).
(рис. 1).
Требуется:
построить эпюру крутящих моментов;
при заданном допускаемом касательном напряжении
 из условия прочности определить диаметр вала, округлив его до ближайшего из следующих значений 30, 35, 40, 45, 50, 60, 70, 80, 90, 100, 200 мм.
из условия прочности определить диаметр вала, округлив его до ближайшего из следующих значений 30, 35, 40, 45, 50, 60, 70, 80, 90, 100, 200 мм.
| Вариант | M1, кН | M2, кН | M3, кН | M, кН |
| 3 | 2,0 | 4,0 | 1,0 | 1,0 |
 рис. 1
рис. 1
Решение
1. Определить реактивный момент, возникающий в жесткой заделке
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
Построить эпюру крутящих моментов по длине вала


____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

Определить диаметр вала из условия прочности
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Практическая работа №14
Кручение стержня круглого сечения
Задача
Жестко защемленный одним концом стальной стержень круглого поперечного сечения скручивается четырьмя моментами  (рис. 1).
(рис. 1).
Требуется:
построить эпюру крутящих моментов;
при заданном допускаемом касательном напряжении
 из условия прочности определить диаметр вала, округлив его до ближайшего из следующих значений 30, 35, 40, 45, 50, 60, 70, 80, 90, 100, 200 мм.
из условия прочности определить диаметр вала, округлив его до ближайшего из следующих значений 30, 35, 40, 45, 50, 60, 70, 80, 90, 100, 200 мм.
| Вариант | M1, кН | M2, кН | M3, кН | M, кН |
| 4 | 3,0 | 5,0 | 1,6 | 1,4 |
 рис. 1
рис. 1
Решение
1. Определить реактивный момент, возникающий в жесткой заделке
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
Построить эпюру крутящих моментов по длине вала


____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

Определить диаметр вала из условия прочности
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Практическая работа №14
Кручение стержня круглого сечения
Задача
Жестко защемленный одним концом стальной стержень круглого поперечного сечения скручивается четырьмя моментами  (рис. 1).
(рис. 1).
Требуется:
построить эпюру крутящих моментов;
при заданном допускаемом касательном напряжении
 из условия прочности определить диаметр вала, округлив его до ближайшего из следующих значений 30, 35, 40, 45, 50, 60, 70, 80, 90, 100, 200 мм.
из условия прочности определить диаметр вала, округлив его до ближайшего из следующих значений 30, 35, 40, 45, 50, 60, 70, 80, 90, 100, 200 мм.
| Вариант | M1, кН | M2, кН | M3, кН | M, кН |
| 5 | 4,0 | 6,0 | 1,8 | 1,4 |
 рис. 1
рис. 1
Решение
1. Определить реактивный момент, возникающий в жесткой заделке
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
Построить эпюру крутящих моментов по длине вала


____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

Определить диаметр вала из условия прочности
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Практическая работа №14
Кручение стержня круглого сечения
Задача
Жестко защемленный одним концом стальной стержень круглого поперечного сечения скручивается четырьмя моментами  (рис. 1).
(рис. 1).
Требуется:
построить эпюру крутящих моментов;
при заданном допускаемом касательном напряжении
 из условия прочности определить диаметр вала, округлив его до ближайшего из следующих значений 30, 35, 40, 45, 50, 60, 70, 80, 90, 100, 200 мм.
из условия прочности определить диаметр вала, округлив его до ближайшего из следующих значений 30, 35, 40, 45, 50, 60, 70, 80, 90, 100, 200 мм.
| Вариант | M1, кН | M2, кН | M3, кН | M, кН |
| 6 | 2,0 | 4,0 | 1,2 | 1,2 |
 рис. 1
рис. 1
Решение
1. Определить реактивный момент, возникающий в жесткой заделке
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
Построить эпюру крутящих моментов по длине вала


____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

Определить диаметр вала из условия прочности
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Практическая работа №14
Кручение стержня круглого сечения
Задача
Жестко защемленный одним концом стальной стержень круглого поперечного сечения скручивается четырьмя моментами  (рис. 1).
(рис. 1).
Требуется:
построить эпюру крутящих моментов;
при заданном допускаемом касательном напряжении
 из условия прочности определить диаметр вала, округлив его до ближайшего из следующих значений 30, 35, 40, 45, 50, 60, 70, 80, 90, 100, 200 мм.
из условия прочности определить диаметр вала, округлив его до ближайшего из следующих значений 30, 35, 40, 45, 50, 60, 70, 80, 90, 100, 200 мм.
| Вариант | M1, кН | M2, кН | M3, кН | M, кН |
| 7 | 2,0 | 3,0 | 1,2 | 1,0 |
 рис. 1
рис. 1
Решение
1. Определить реактивный момент, возникающий в жесткой заделке
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
Построить эпюру крутящих моментов по длине вала


____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

Определить диаметр вала из условия прочности
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Практическая работа №14
Кручение стержня круглого сечения
Задача
Жестко защемленный одним концом стальной стержень круглого поперечного сечения скручивается четырьмя моментами  (рис. 1).
(рис. 1).
Требуется:
построить эпюру крутящих моментов;
при заданном допускаемом касательном напряжении
 из условия прочности определить диаметр вала, округлив его до ближайшего из следующих значений 30, 35, 40, 45, 50, 60, 70, 80, 90, 100, 200 мм.
из условия прочности определить диаметр вала, округлив его до ближайшего из следующих значений 30, 35, 40, 45, 50, 60, 70, 80, 90, 100, 200 мм.
| Вариант | M1, кН | M2, кН | M3, кН | M, кН |
| 8 | 3,0 | 4,0 | 1,0 | 1,0 |
 рис. 1
рис. 1
Решение
1. Определить реактивный момент, возникающий в жесткой заделке
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
Построить эпюру крутящих моментов по длине вала


____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

Определить диаметр вала из условия прочности
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Практическая работа №14
Кручение стержня круглого сечения
Задача
Жестко защемленный одним концом стальной стержень круглого поперечного сечения скручивается четырьмя моментами  (рис. 1).
(рис. 1).
Требуется:
построить эпюру крутящих моментов;
при заданном допускаемом касательном напряжении
 из условия прочности определить диаметр вала, округлив его до ближайшего из следующих значений 30, 35, 40, 45, 50, 60, 70, 80, 90, 100, 200 мм.
из условия прочности определить диаметр вала, округлив его до ближайшего из следующих значений 30, 35, 40, 45, 50, 60, 70, 80, 90, 100, 200 мм.
| Вариант | M1, кН | M2, кН | M3, кН | M, кН |
| 9 | 4,0 | 5,0 | 1,8 | 1,6 |
 рис. 1
рис. 1
Решение
1. Определить реактивный момент, возникающий в жесткой заделке
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
Построить эпюру крутящих моментов по длине вала


____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

Определить диаметр вала из условия прочности
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Практическая работа №14
Кручение стержня круглого сечения
Задача
Жестко защемленный одним концом стальной стержень круглого поперечного сечения скручивается четырьмя моментами  (рис. 1).
(рис. 1).
Требуется:
построить эпюру крутящих моментов;
при заданном допускаемом касательном напряжении
 из условия прочности определить диаметр вала, округлив его до ближайшего из следующих значений 30, 35, 40, 45, 50, 60, 70, 80, 90, 100, 200 мм.
из условия прочности определить диаметр вала, округлив его до ближайшего из следующих значений 30, 35, 40, 45, 50, 60, 70, 80, 90, 100, 200 мм.
| Вариант | M1, кН | M2, кН | M3, кН | M, кН |
| 10 | 5,0 | 6,0 | 2,0 | 1,6 |
 рис. 1
рис. 1
Решение
1. Определить реактивный момент, возникающий в жесткой заделке
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
Построить эпюру крутящих моментов по длине вала


____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

Определить диаметр вала из условия прочности
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Практическая работа №14
Кручение стержня круглого сечения
Задача
Жестко защемленный одним концом стальной стержень круглого поперечного сечения скручивается четырьмя моментами  (рис. 1).
(рис. 1).
Требуется:
построить эпюру крутящих моментов;
при заданном допускаемом касательном напряжении
 из условия прочности определить диаметр вала, округлив его до ближайшего из следующих значений 30, 35, 40, 45, 50, 60, 70, 80, 90, 100, 200 мм.
из условия прочности определить диаметр вала, округлив его до ближайшего из следующих значений 30, 35, 40, 45, 50, 60, 70, 80, 90, 100, 200 мм.
| Вариант | M1, кН | M2, кН | M3, кН | M, кН |
| 11 | 2,0 | 4,0 | 1,4 | 1,0 |
 рис. 1
рис. 1
Решение
1. Определить реактивный момент, возникающий в жесткой заделке
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
Построить эпюру крутящих моментов по длине вала


____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

Определить диаметр вала из условия прочности
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Практическая работа №14
Кручение стержня круглого сечения
Задача
Жестко защемленный одним концом стальной стержень круглого поперечного сечения скручивается четырьмя моментами  (рис. 1).
(рис. 1).
Требуется:
построить эпюру крутящих моментов;
при заданном допускаемом касательном напряжении
 из условия прочности определить диаметр вала, округлив его до ближайшего из следующих значений 30, 35, 40, 45, 50, 60, 70, 80, 90, 100, 200 мм.
из условия прочности определить диаметр вала, округлив его до ближайшего из следующих значений 30, 35, 40, 45, 50, 60, 70, 80, 90, 100, 200 мм.
| Вариант | M1, кН | M2, кН | M3, кН | M, кН |
| 12 | 1,0 | 4,0 | 2,0 | 0,8 |
 рис. 1
рис. 1
Решение
1. Определить реактивный момент, возникающий в жесткой заделке
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
Построить эпюру крутящих моментов по длине вала


____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

Определить диаметр вала из условия прочности
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Практическая работа №14
Кручение стержня круглого сечения
Задача
Жестко защемленный одним концом стальной стержень круглого поперечного сечения скручивается четырьмя моментами  (рис. 1).
(рис. 1).
Требуется:
построить эпюру крутящих моментов;
при заданном допускаемом касательном напряжении
 из условия прочности определить диаметр вала, округлив его до ближайшего из следующих значений 30, 35, 40, 45, 50, 60, 70, 80, 90, 100, 200 мм.
из условия прочности определить диаметр вала, округлив его до ближайшего из следующих значений 30, 35, 40, 45, 50, 60, 70, 80, 90, 100, 200 мм.
| Вариант | M1, кН | M2, кН | M3, кН | M, кН |
| 13 | 2,0 | 4,0 | 2,0 | 2,0 |
 рис. 1
рис. 1
Решение
1. Определить реактивный момент, возникающий в жесткой заделке
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
Построить эпюру крутящих моментов по длине вала


____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

Определить диаметр вала из условия прочности
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Практическая работа №14
Кручение стержня круглого сечения
Задача
Жестко защемленный одним концом стальной стержень круглого поперечного сечения скручивается четырьмя моментами  (рис. 1).
(рис. 1).
Требуется:
построить эпюру крутящих моментов;
при заданном допускаемом касательном напряжении
 из условия прочности определить диаметр вала, округлив его до ближайшего из следующих значений 30, 35, 40, 45, 50, 60, 70, 80, 90, 100, 200 мм.
из условия прочности определить диаметр вала, округлив его до ближайшего из следующих значений 30, 35, 40, 45, 50, 60, 70, 80, 90, 100, 200 мм.
| Вариант | M1, кН | M2, кН | M3, кН | M, кН |
| 14 | 2,0 | 5,0 | 1,0 | 1,4 |
 рис. 1
рис. 1
Решение
1. Определить реактивный момент, возникающий в жесткой заделке
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
Построить эпюру крутящих моментов по длине вала


____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

Определить диаметр вала из условия прочности
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Практическая работа №14
Кручение стержня круглого сечения
Задача
Жестко защемленный одним концом стальной стержень круглого поперечного сечения скручивается четырьмя моментами  (рис. 1).
(рис. 1).
Требуется:
построить эпюру крутящих моментов;
при заданном допускаемом касательном напряжении
 из условия прочности определить диаметр вала, округлив его до ближайшего из следующих значений 30, 35, 40, 45, 50, 60, 70, 80, 90, 100, 200 мм.
из условия прочности определить диаметр вала, округлив его до ближайшего из следующих значений 30, 35, 40, 45, 50, 60, 70, 80, 90, 100, 200 мм.
| Вариант | M1, кН | M2, кН | M3, кН | M, кН |
| 15 | 3,0 | 5,0 | 1,6 | 1,4 |
 рис. 1
рис. 1
Решение
1. Определить реактивный момент, возникающий в жесткой заделке
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
Построить эпюру крутящих моментов по длине вала


____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

Определить диаметр вала из условия прочности
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Практическая работа №14
Кручение стержня круглого сечения
Задача
Жестко защемленный одним концом стальной стержень круглого поперечного сечения скручивается четырьмя моментами  (рис. 1).
(рис. 1).
Требуется:
построить эпюру крутящих моментов;
при заданном допускаемом касательном напряжении
 из условия прочности определить диаметр вала, округлив его до ближайшего из следующих значений 30, 35, 40, 45, 50, 60, 70, 80, 90, 100, 200 мм.
из условия прочности определить диаметр вала, округлив его до ближайшего из следующих значений 30, 35, 40, 45, 50, 60, 70, 80, 90, 100, 200 мм.
| Вариант | M1, кН | M2, кН | M3, кН | M, кН |
| 16 | 2,0 | 6,0 | 1,0 | 1,0 |
 рис. 1
рис. 1
Решение
1. Определить реактивный момент, возникающий в жесткой заделке
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
Построить эпюру крутящих моментов по длине вала


____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

Определить диаметр вала из условия прочности
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Практическая работа №14
Кручение стержня круглого сечения
Задача
Жестко защемленный одним концом стальной стержень круглого поперечного сечения скручивается четырьмя моментами  (рис. 1).
(рис. 1).
Требуется:
построить эпюру крутящих моментов;
при заданном допускаемом касательном напряжении
 из условия прочности определить диаметр вала, округлив его до ближайшего из следующих значений 30, 35, 40, 45, 50, 60, 70, 80, 90, 100, 200 мм.
из условия прочности определить диаметр вала, округлив его до ближайшего из следующих значений 30, 35, 40, 45, 50, 60, 70, 80, 90, 100, 200 мм.
| Вариант | M1, кН | M2, кН | M3, кН | M, кН |
| 17 | 1,0 | 4,0 | 1,0 | 1,0 |
 рис. 1
рис. 1
Решение
1. Определить реактивный момент, возникающий в жесткой заделке
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
Построить эпюру крутящих моментов по длине вала


____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

Определить диаметр вала из условия прочности
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Практическая работа №14
Кручение стержня круглого сечения
Задача
Жестко защемленный одним концом стальной стержень круглого поперечного сечения скручивается четырьмя моментами  (рис. 1).
(рис. 1).
Требуется:
построить эпюру крутящих моментов;
при заданном допускаемом касательном напряжении
 из условия прочности определить диаметр вала, округлив его до ближайшего из следующих значений 30, 35, 40, 45, 50, 60, 70, 80, 90, 100, 200 мм.
из условия прочности определить диаметр вала, округлив его до ближайшего из следующих значений 30, 35, 40, 45, 50, 60, 70, 80, 90, 100, 200 мм.
| Вариант | M1, кН | M2, кН | M3, кН | M, кН |
| 18 | 4,0 | 6,0 | 1,2 | 1,2 |
 рис. 1
рис. 1
Решение
1. Определить реактивный момент, возникающий в жесткой заделке
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
Построить эпюру крутящих моментов по длине вала


____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

Определить диаметр вала из условия прочности
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Практическая работа №14
Кручение стержня круглого сечения
Задача
Жестко защемленный одним концом стальной стержень круглого поперечного сечения скручивается четырьмя моментами  (рис. 1).
(рис. 1).
Требуется:
построить эпюру крутящих моментов;
при заданном допускаемом касательном напряжении
 из условия прочности определить диаметр вала, округлив его до ближайшего из следующих значений 30, 35, 40, 45, 50, 60, 70, 80, 90, 100, 200 мм.
из условия прочности определить диаметр вала, округлив его до ближайшего из следующих значений 30, 35, 40, 45, 50, 60, 70, 80, 90, 100, 200 мм.
| Вариант | M1, кН | M2, кН | M3, кН | M, кН |
| 19 | 2,0 | 4,0 | 1,6 | 1,6 |
 рис. 1
рис. 1
Решение
1. Определить реактивный момент, возникающий в жесткой заделке
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
Построить эпюру крутящих моментов по длине вала


____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

Определить диаметр вала из условия прочности
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Практическая работа №14
Кручение стержня круглого сечения
Задача
Жестко защемленный одним концом стальной стержень круглого поперечного сечения скручивается четырьмя моментами  (рис. 1).
(рис. 1).
Требуется:
построить эпюру крутящих моментов;
при заданном допускаемом касательном напряжении
 из условия прочности определить диаметр вала, округлив его до ближайшего из следующих значений 30, 35, 40, 45, 50, 60, 70, 80, 90, 100, 200 мм.
из условия прочности определить диаметр вала, округлив его до ближайшего из следующих значений 30, 35, 40, 45, 50, 60, 70, 80, 90, 100, 200 мм.
| Вариант | M1, кН | M2, кН | M3, кН | M, кН |
| 20 | 2,0 | 4,0 | 2,0 | 2,0 |
 рис. 1
рис. 1
Решение
1. Определить реактивный момент, возникающий в жесткой заделке
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
Построить эпюру крутящих моментов по длине вала


____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

Определить диаметр вала из условия прочности
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Практическая работа №14
Кручение стержня круглого сечения
Задача
Жестко защемленный одним концом стальной стержень круглого поперечного сечения скручивается четырьмя моментами  (рис. 1).
(рис. 1).
Требуется:
построить эпюру крутящих моментов;
при заданном допускаемом касательном напряжении
 из условия прочности определить диаметр вала, округлив его до ближайшего из следующих значений 30, 35, 40, 45, 50, 60, 70, 80, 90, 100, 200 мм.
из условия прочности определить диаметр вала, округлив его до ближайшего из следующих значений 30, 35, 40, 45, 50, 60, 70, 80, 90, 100, 200 мм.
| Вариант | M1, кН | M2, кН | M3, кН | M, кН |
| 21 | 1,0 | 4,0 | 1,0 | 1,4 |
 рис. 1
рис. 1
Решение
1. Определить реактивный момент, возникающий в жесткой заделке
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
Построить эпюру крутящих моментов по длине вала


____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

Определить диаметр вала из условия прочности
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Практическая работа №14
Кручение стержня круглого сечения
Задача
Жестко защемленный одним концом стальной стержень круглого поперечного сечения скручивается четырьмя моментами  (рис. 1).
(рис. 1).
Требуется:
построить эпюру крутящих моментов;
при заданном допускаемом касательном напряжении
 из условия прочности определить диаметр вала, округлив его до ближайшего из следующих значений 30, 35, 40, 45, 50, 60, 70, 80, 90, 100, 200 мм.
из условия прочности определить диаметр вала, округлив его до ближайшего из следующих значений 30, 35, 40, 45, 50, 60, 70, 80, 90, 100, 200 мм.
| Вариант | M1, кН | M2, кН | M3, кН | M, кН |
| 22 | 3,0 | 5,0 | 1,4 | 1,4 |
 рис. 1
рис. 1
Решение
1. Определить реактивный момент, возникающий в жесткой заделке
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
Построить эпюру крутящих моментов по длине вала


____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

Определить диаметр вала из условия прочности
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Практическая работа №14
Кручение стержня круглого сечения
Задача
Жестко защемленный одним концом стальной стержень круглого поперечного сечения скручивается четырьмя моментами  (рис. 1).
(рис. 1).
Требуется:
построить эпюру крутящих моментов;
при заданном допускаемом касательном напряжении
 из условия прочности определить диаметр вала, округлив его до ближайшего из следующих значений 30, 35, 40, 45, 50, 60, 70, 80, 90, 100, 200 мм.
из условия прочности определить диаметр вала, округлив его до ближайшего из следующих значений 30, 35, 40, 45, 50, 60, 70, 80, 90, 100, 200 мм.
| Вариант | M1, кН | M2, кН | M3, кН | M, кН |
| 23 | 2,0 | 4,0 | 1,2 | 1,0 |
 рис. 1
рис. 1
Решение
1. Определить реактивный момент, возникающий в жесткой заделке
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
Построить эпюру крутящих моментов по длине вала


____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

Определить диаметр вала из условия прочности
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Практическая работа №14
Кручение стержня круглого сечения
Задача
Жестко защемленный одним концом стальной стержень круглого поперечного сечения скручивается четырьмя моментами  (рис. 1).
(рис. 1).
Требуется:
построить эпюру крутящих моментов;
при заданном допускаемом касательном напряжении
 из условия прочности определить диаметр вала, округлив его до ближайшего из следующих значений 30, 35, 40, 45, 50, 60, 70, 80, 90, 100, 200 мм.
из условия прочности определить диаметр вала, округлив его до ближайшего из следующих значений 30, 35, 40, 45, 50, 60, 70, 80, 90, 100, 200 мм.
| Вариант | M1, кН | M2, кН | M3, кН | M, кН |
| 24 | 2,0 | 5,0 | 1,0 | 1,0 |
 рис. 1
рис. 1
Решение
1. Определить реактивный момент, возникающий в жесткой заделке
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
Построить эпюру крутящих моментов по длине вала


____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

Определить диаметр вала из условия прочности
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Практическая работа №14
Кручение стержня круглого сечения
Задача
Жестко защемленный одним концом стальной стержень круглого поперечного сечения скручивается четырьмя моментами  (рис. 1).
(рис. 1).
Требуется:
построить эпюру крутящих моментов;
при заданном допускаемом касательном напряжении
 из условия прочности определить диаметр вала, округлив его до ближайшего из следующих значений 30, 35, 40, 45, 50, 60, 70, 80, 90, 100, 200 мм.
из условия прочности определить диаметр вала, округлив его до ближайшего из следующих значений 30, 35, 40, 45, 50, 60, 70, 80, 90, 100, 200 мм.
| Вариант | M1, кН | M2, кН | M3, кН | M, кН |
| 25 | 1,0 | 3,0 | 1,0 | 1,6 |
 рис. 1
рис. 1
Решение
1. Определить реактивный момент, возникающий в жесткой заделке
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
Построить эпюру крутящих моментов по длине вала


____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

Определить диаметр вала из условия прочности
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Просмотр содержимого документа
«Практическая работа №15»
Практическая работа №15
Построение эпюр поперечных сил и изгибающих моментов.
Расчеты на прочность
Задача
Для двухопорной балки (рис. 1), нагруженной сосредоточенными силами и парой сил с моментом, определить реакции в опорах, построить эпюры поперечных сил и изгибающих моментов. Найти максимальный момент, и используя условие прочности, подобрать необходимые размеры поперечных сечений. Материал – сталь, допускаемое напряжение изгиба 160 МПа. Сечение – швеллер.
| Вариант | F1, кН | F2, кН | m, кН | а, м |
| 1 | 10 | 4,4 | 3 | 0,2 |
 рис. 1
рис. 1
Решение
1. Определить реакции в опорах балки
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
Для построения эпюры поперечных сил и изгибающих моментов, провести расчет по характерным точкам
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
Построение эпюры поперечных сил и изгибающих моментов

Подобрать необходимые размеры поперечных сечений
Условие прочности при изгибе:
 ,
,
откуда

____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
Практическая работа №15
Построение эпюр поперечных сил и изгибающих моментов.
Расчеты на прочность
Задача
Для двухопорной балки (рис. 1), нагруженной сосредоточенными силами и парой сил с моментом, определить реакции в опорах, построить эпюры поперечных сил и изгибающих моментов. Найти максимальный момент, и используя условие прочности, подобрать необходимые размеры поперечных сечений. Материал – сталь, допускаемое напряжение изгиба 160 МПа. Сечение – швеллер.
| Вариант | F1, кН | F2, кН | m, кН | а, м |
| 2 | 11 | 4,8 | 4 | 0,2 |
 рис. 1
рис. 1
Решение
1. Определить реакции в опорах балки
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
Для построения эпюры поперечных сил и изгибающих моментов, провести расчет по характерным точкам
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
Построение эпюры поперечных сил и изгибающих моментов

Подобрать необходимые размеры поперечных сечений
Условие прочности при изгибе:
 ,
,
откуда

____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
Практическая работа №15
Построение эпюр поперечных сил и изгибающих моментов.
Расчеты на прочность
Задача
Для двухопорной балки (рис. 1), нагруженной сосредоточенными силами и парой сил с моментом, определить реакции в опорах, построить эпюры поперечных сил и изгибающих моментов. Найти максимальный момент, и используя условие прочности, подобрать необходимые размеры поперечных сечений. Материал – сталь, допускаемое напряжение изгиба 160 МПа. Сечение – швеллер.
| Вариант | F1, кН | F2, кН | m, кН | а, м |
| 3 | 12 | 7,8 | 5 | 0,3 |
 рис. 1
рис. 1
Решение
1. Определить реакции в опорах балки
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
Для построения эпюры поперечных сил и изгибающих моментов, провести расчет по характерным точкам
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
Построение эпюры поперечных сил и изгибающих моментов

Подобрать необходимые размеры поперечных сечений
Условие прочности при изгибе:
 ,
,
откуда

____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
Практическая работа №15
Построение эпюр поперечных сил и изгибающих моментов.
Расчеты на прочность
Задача
Для двухопорной балки (рис. 1), нагруженной сосредоточенными силами и парой сил с моментом, определить реакции в опорах, построить эпюры поперечных сил и изгибающих моментов. Найти максимальный момент, и используя условие прочности, подобрать необходимые размеры поперечных сечений. Материал – сталь, допускаемое напряжение изгиба 160 МПа. Сечение – швеллер.
| Вариант | F1, кН | F2, кН | m, кН | а, м |
| 4 | 13 | 8,4 | 6 | 0,3 |
 рис. 1
рис. 1
Решение
1. Определить реакции в опорах балки
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
Для построения эпюры поперечных сил и изгибающих моментов, провести расчет по характерным точкам
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
Построение эпюры поперечных сил и изгибающих моментов

Подобрать необходимые размеры поперечных сечений
Условие прочности при изгибе:
 ,
,
откуда

____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
Практическая работа №15
Построение эпюр поперечных сил и изгибающих моментов.
Расчеты на прочность
Задача
Для двухопорной балки (рис. 1), нагруженной сосредоточенными силами и парой сил с моментом, определить реакции в опорах, построить эпюры поперечных сил и изгибающих моментов. Найти максимальный момент, и используя условие прочности, подобрать необходимые размеры поперечных сечений. Материал – сталь, допускаемое напряжение изгиба 160 МПа. Сечение – швеллер.
| Вариант | F1, кН | F2, кН | m, кН | а, м |
| 5 | 14 | 12 | 7 | 0,4 |
 рис. 1
рис. 1
Решение
1. Определить реакции в опорах балки
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
Для построения эпюры поперечных сил и изгибающих моментов, провести расчет по характерным точкам
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
Построение эпюры поперечных сил и изгибающих моментов

Подобрать необходимые размеры поперечных сечений
Условие прочности при изгибе:
 ,
,
откуда

____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
Практическая работа №15
Построение эпюр поперечных сил и изгибающих моментов.
Расчеты на прочность
Задача
Для двухопорной балки (рис. 1), нагруженной сосредоточенными силами и парой сил с моментом, определить реакции в опорах, построить эпюры поперечных сил и изгибающих моментов. Найти максимальный момент, и используя условие прочности, подобрать необходимые размеры поперечных сечений. Материал – сталь, допускаемое напряжение изгиба 160 МПа. Сечение – швеллер.
| Вариант | F1, кН | F2, кН | m, кН | а, м |
| 6 | 15 | 12,8 | 7 | 0,4 |
 рис. 1
рис. 1
Решение
1. Определить реакции в опорах балки
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
Для построения эпюры поперечных сил и изгибающих моментов, провести расчет по характерным точкам
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
Построение эпюры поперечных сил и изгибающих моментов

Подобрать необходимые размеры поперечных сечений
Условие прочности при изгибе:
 ,
,
откуда

____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
Практическая работа №15
Построение эпюр поперечных сил и изгибающих моментов.
Расчеты на прочность
Задача
Для двухопорной балки (рис. 1), нагруженной сосредоточенными силами и парой сил с моментом, определить реакции в опорах, построить эпюры поперечных сил и изгибающих моментов. Найти максимальный момент, и используя условие прочности, подобрать необходимые размеры поперечных сечений. Материал – сталь, допускаемое напряжение изгиба 160 МПа. Сечение – швеллер.
| Вариант | F1, кН | F2, кН | m, кН | а, м |
| 7 | 16 | 17 | 6 | 0,5 |
 рис. 1
рис. 1
Решение
1. Определить реакции в опорах балки
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
Для построения эпюры поперечных сил и изгибающих моментов, провести расчет по характерным точкам
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
Построение эпюры поперечных сил и изгибающих моментов

Подобрать необходимые размеры поперечных сечений
Условие прочности при изгибе:
 ,
,
откуда

____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
Практическая работа №15
Построение эпюр поперечных сил и изгибающих моментов.
Расчеты на прочность
Задача
Для двухопорной балки (рис. 1), нагруженной сосредоточенными силами и парой сил с моментом, определить реакции в опорах, построить эпюры поперечных сил и изгибающих моментов. Найти максимальный момент, и используя условие прочности, подобрать необходимые размеры поперечных сечений. Материал – сталь, допускаемое напряжение изгиба 160 МПа. Сечение – швеллер.
| Вариант | F1, кН | F2, кН | m, кН | а, м |
| 8 | 17 | 18 | 5 | 0,5 |
 рис. 1
рис. 1
Решение
1. Определить реакции в опорах балки
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
Для построения эпюры поперечных сил и изгибающих моментов, провести расчет по характерным точкам
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
Построение эпюры поперечных сил и изгибающих моментов

Подобрать необходимые размеры поперечных сечений
Условие прочности при изгибе:
 ,
,
откуда

____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
Практическая работа №15
Построение эпюр поперечных сил и изгибающих моментов.
Расчеты на прочность
Задача
Для двухопорной балки (рис. 1), нагруженной сосредоточенными силами и парой сил с моментом, определить реакции в опорах, построить эпюры поперечных сил и изгибающих моментов. Найти максимальный момент, и используя условие прочности, подобрать необходимые размеры поперечных сечений. Материал – сталь, допускаемое напряжение изгиба 160 МПа. Сечение – швеллер.
| Вариант | F1, кН | F2, кН | m, кН | а, м |
| 9 | 18 | 22,8 | 4 | 0,6 |
 рис. 1
рис. 1
Решение
1. Определить реакции в опорах балки
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
Для построения эпюры поперечных сил и изгибающих моментов, провести расчет по характерным точкам
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
Построение эпюры поперечных сил и изгибающих моментов

Подобрать необходимые размеры поперечных сечений
Условие прочности при изгибе:
 ,
,
откуда

____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
Практическая работа №15
Построение эпюр поперечных сил и изгибающих моментов.
Расчеты на прочность
Задача
Для двухопорной балки (рис. 1), нагруженной сосредоточенными силами и парой сил с моментом, определить реакции в опорах, построить эпюры поперечных сил и изгибающих моментов. Найти максимальный момент, и используя условие прочности, подобрать необходимые размеры поперечных сечений. Материал – сталь, допускаемое напряжение изгиба 160 МПа. Сечение – швеллер.
| Вариант | F1, кН | F2, кН | m, кН | а, м |
| 10 | 19 | 24 | 3 | 0,6 |
 рис. 1
рис. 1
Решение
1. Определить реакции в опорах балки
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
Для построения эпюры поперечных сил и изгибающих моментов, провести расчет по характерным точкам
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
Построение эпюры поперечных сил и изгибающих моментов

Подобрать необходимые размеры поперечных сечений
Условие прочности при изгибе:
 ,
,
откуда

____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
Практическая работа №15
Построение эпюр поперечных сил и изгибающих моментов.
Расчеты на прочность
Задача
Для двухопорной балки (рис. 1), нагруженной сосредоточенными силами и парой сил с моментом, определить реакции в опорах, построить эпюры поперечных сил и изгибающих моментов. Найти максимальный момент, и используя условие прочности, подобрать необходимые размеры поперечных сечений. Материал – сталь, допускаемое напряжение изгиба 160 МПа. Сечение – швеллер.
| Вариант | F1, кН | F2, кН | m, кН | а, м |
| 11 | 15 | 12,8 | 7 | 0,4 |
 рис. 1
рис. 1
Решение
1. Определить реакции в опорах балки
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
Для построения эпюры поперечных сил и изгибающих моментов, провести расчет по характерным точкам
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
Построение эпюры поперечных сил и изгибающих моментов

Подобрать необходимые размеры поперечных сечений
Условие прочности при изгибе:
 ,
,
откуда

____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
Практическая работа №15
Построение эпюр поперечных сил и изгибающих моментов.
Расчеты на прочность
Задача
Для двухопорной балки (рис. 1), нагруженной сосредоточенными силами и парой сил с моментом, определить реакции в опорах, построить эпюры поперечных сил и изгибающих моментов. Найти максимальный момент, и используя условие прочности, подобрать необходимые размеры поперечных сечений. Материал – сталь, допускаемое напряжение изгиба 160 МПа. Сечение – швеллер.
| Вариант | F1, кН | F2, кН | m, кН | а, м |
| 12 | 16 | 17 | 6 | 0,5 |
 рис. 1
рис. 1
Решение
1. Определить реакции в опорах балки
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
Для построения эпюры поперечных сил и изгибающих моментов, провести расчет по характерным точкам
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
Построение эпюры поперечных сил и изгибающих моментов

Подобрать необходимые размеры поперечных сечений
Условие прочности при изгибе:
 ,
,
откуда

____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
Практическая работа №15
Построение эпюр поперечных сил и изгибающих моментов.
Расчеты на прочность
Задача
Для двухопорной балки (рис. 1), нагруженной сосредоточенными силами и парой сил с моментом, определить реакции в опорах, построить эпюры поперечных сил и изгибающих моментов. Найти максимальный момент, и используя условие прочности, подобрать необходимые размеры поперечных сечений. Материал – сталь, допускаемое напряжение изгиба 160 МПа. Сечение – швеллер.
| Вариант | F1, кН | F2, кН | m, кН | а, м |
| 13 | 17 | 18 | 5 | 0,5 |
 рис. 1
рис. 1
Решение
1. Определить реакции в опорах балки
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
Для построения эпюры поперечных сил и изгибающих моментов, провести расчет по характерным точкам
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
Построение эпюры поперечных сил и изгибающих моментов

Подобрать необходимые размеры поперечных сечений
Условие прочности при изгибе:
 ,
,
откуда

____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
Практическая работа №15
Построение эпюр поперечных сил и изгибающих моментов.
Расчеты на прочность
Задача
Для двухопорной балки (рис. 1), нагруженной сосредоточенными силами и парой сил с моментом, определить реакции в опорах, построить эпюры поперечных сил и изгибающих моментов. Найти максимальный момент, и используя условие прочности, подобрать необходимые размеры поперечных сечений. Материал – сталь, допускаемое напряжение изгиба 160 МПа. Сечение – швеллер.
| Вариант | F1, кН | F2, кН | m, кН | а, м |
| 14 | 18 | 22,8 | 4 | 0,6 |
 рис. 1
рис. 1
Решение
1. Определить реакции в опорах балки
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
Для построения эпюры поперечных сил и изгибающих моментов, провести расчет по характерным точкам
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
Построение эпюры поперечных сил и изгибающих моментов

Подобрать необходимые размеры поперечных сечений
Условие прочности при изгибе:
 ,
,
откуда

____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
Практическая работа №15
Построение эпюр поперечных сил и изгибающих моментов.
Расчеты на прочность
Задача
Для двухопорной балки (рис. 1), нагруженной сосредоточенными силами и парой сил с моментом, определить реакции в опорах, построить эпюры поперечных сил и изгибающих моментов. Найти максимальный момент, и используя условие прочности, подобрать необходимые размеры поперечных сечений. Материал – сталь, допускаемое напряжение изгиба 160 МПа. Сечение – швеллер.
| Вариант | F1, кН | F2, кН | m, кН | а, м |
| 15 | 19 | 24 | 3 | 0,6 |
 рис. 1
рис. 1
Решение
1. Определить реакции в опорах балки
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
Для построения эпюры поперечных сил и изгибающих моментов, провести расчет по характерным точкам
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
Построение эпюры поперечных сил и изгибающих моментов

Подобрать необходимые размеры поперечных сечений
Условие прочности при изгибе:
 ,
,
откуда

____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
Практическая работа №15
Построение эпюр поперечных сил и изгибающих моментов.
Расчеты на прочность
Задача
Для двухопорной балки (рис. 1), нагруженной сосредоточенными силами и парой сил с моментом, определить реакции в опорах, построить эпюры поперечных сил и изгибающих моментов. Найти максимальный момент, и используя условие прочности, подобрать необходимые размеры поперечных сечений. Материал – сталь, допускаемое напряжение изгиба 160 МПа. Сечение – швеллер.
| Вариант | F1, кН | F2, кН | m, кН | а, м |
| 16 | 10 | 4,4 | 3 | 0,2 |
 рис. 1
рис. 1
Решение
1. Определить реакции в опорах балки
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
Для построения эпюры поперечных сил и изгибающих моментов, провести расчет по характерным точкам
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
Построение эпюры поперечных сил и изгибающих моментов

Подобрать необходимые размеры поперечных сечений
Условие прочности при изгибе:
 ,
,
откуда

____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
Практическая работа №15
Построение эпюр поперечных сил и изгибающих моментов.
Расчеты на прочность
Задача
Для двухопорной балки (рис. 1), нагруженной сосредоточенными силами и парой сил с моментом, определить реакции в опорах, построить эпюры поперечных сил и изгибающих моментов. Найти максимальный момент, и используя условие прочности, подобрать необходимые размеры поперечных сечений. Материал – сталь, допускаемое напряжение изгиба 160 МПа. Сечение – швеллер.
| Вариант | F1, кН | F2, кН | m, кН | а, м |
| 17 | 11 | 4,8 | 4 | 0,2 |
 рис. 1
рис. 1
Решение
1. Определить реакции в опорах балки
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
Для построения эпюры поперечных сил и изгибающих моментов, провести расчет по характерным точкам
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
Построение эпюры поперечных сил и изгибающих моментов

Подобрать необходимые размеры поперечных сечений
Условие прочности при изгибе:
 ,
,
откуда

____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
Практическая работа №15
Построение эпюр поперечных сил и изгибающих моментов.
Расчеты на прочность
Задача
Для двухопорной балки (рис. 1), нагруженной сосредоточенными силами и парой сил с моментом, определить реакции в опорах, построить эпюры поперечных сил и изгибающих моментов. Найти максимальный момент, и используя условие прочности, подобрать необходимые размеры поперечных сечений. Материал – сталь, допускаемое напряжение изгиба 160 МПа. Сечение – швеллер.
| Вариант | F1, кН | F2, кН | m, кН | а, м |
| 18 | 12 | 7,8 | 5 | 0,3 |
 рис. 1
рис. 1
Решение
1. Определить реакции в опорах балки
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
Для построения эпюры поперечных сил и изгибающих моментов, провести расчет по характерным точкам
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
Построение эпюры поперечных сил и изгибающих моментов

Подобрать необходимые размеры поперечных сечений
Условие прочности при изгибе:
 ,
,
откуда

____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
Практическая работа №15
Построение эпюр поперечных сил и изгибающих моментов.
Расчеты на прочность
Задача
Для двухопорной балки (рис. 1), нагруженной сосредоточенными силами и парой сил с моментом, определить реакции в опорах, построить эпюры поперечных сил и изгибающих моментов. Найти максимальный момент, и используя условие прочности, подобрать необходимые размеры поперечных сечений. Материал – сталь, допускаемое напряжение изгиба 160 МПа. Сечение – швеллер.
| Вариант | F1, кН | F2, кН | m, кН | а, м |
| 19 | 13 | 8,4 | 6 | 0,3 |
 рис. 1
рис. 1
Решение
1. Определить реакции в опорах балки
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
Для построения эпюры поперечных сил и изгибающих моментов, провести расчет по характерным точкам
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
Построение эпюры поперечных сил и изгибающих моментов

Подобрать необходимые размеры поперечных сечений
Условие прочности при изгибе:
 ,
,
откуда

____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
Практическая работа №15
Построение эпюр поперечных сил и изгибающих моментов.
Расчеты на прочность
Задача
Для двухопорной балки (рис. 1), нагруженной сосредоточенными силами и парой сил с моментом, определить реакции в опорах, построить эпюры поперечных сил и изгибающих моментов. Найти максимальный момент, и используя условие прочности, подобрать необходимые размеры поперечных сечений. Материал – сталь, допускаемое напряжение изгиба 160 МПа. Сечение – швеллер.
| Вариант | F1, кН | F2, кН | m, кН | а, м |
| 20 | 14 | 12 | 7 | 0,4 |
 рис. 1
рис. 1
Решение
1. Определить реакции в опорах балки
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
Для построения эпюры поперечных сил и изгибающих моментов, провести расчет по характерным точкам
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
Построение эпюры поперечных сил и изгибающих моментов

Подобрать необходимые размеры поперечных сечений
Условие прочности при изгибе:
 ,
,
откуда

____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
Практическая работа №15
Построение эпюр поперечных сил и изгибающих моментов.
Расчеты на прочность
Задача
Для двухопорной балки (рис. 1), нагруженной сосредоточенными силами и парой сил с моментом, определить реакции в опорах, построить эпюры поперечных сил и изгибающих моментов. Найти максимальный момент, и используя условие прочности, подобрать необходимые размеры поперечных сечений. Материал – сталь, допускаемое напряжение изгиба 160 МПа. Сечение – швеллер.
| Вариант | F1, кН | F2, кН | m, кН | а, м |
| 21 | 15 | 12,8 | 7 | 0,4 |
 рис. 1
рис. 1
Решение
1. Определить реакции в опорах балки
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
Для построения эпюры поперечных сил и изгибающих моментов, провести расчет по характерным точкам
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
Построение эпюры поперечных сил и изгибающих моментов

Подобрать необходимые размеры поперечных сечений
Условие прочности при изгибе:
 ,
,
откуда

____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
Практическая работа №15
Построение эпюр поперечных сил и изгибающих моментов.
Расчеты на прочность
Задача
Для двухопорной балки (рис. 1), нагруженной сосредоточенными силами и парой сил с моментом, определить реакции в опорах, построить эпюры поперечных сил и изгибающих моментов. Найти максимальный момент, и используя условие прочности, подобрать необходимые размеры поперечных сечений. Материал – сталь, допускаемое напряжение изгиба 160 МПа. Сечение – швеллер.
| Вариант | F1, кН | F2, кН | m, кН | а, м |
| 22 | 16 | 17 | 6 | 0,5 |
 рис. 1
рис. 1
Решение
1. Определить реакции в опорах балки
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
Для построения эпюры поперечных сил и изгибающих моментов, провести расчет по характерным точкам
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
Построение эпюры поперечных сил и изгибающих моментов

Подобрать необходимые размеры поперечных сечений
Условие прочности при изгибе:
 ,
,
откуда

____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
Практическая работа №15
Построение эпюр поперечных сил и изгибающих моментов.
Расчеты на прочность
Задача
Для двухопорной балки (рис. 1), нагруженной сосредоточенными силами и парой сил с моментом, определить реакции в опорах, построить эпюры поперечных сил и изгибающих моментов. Найти максимальный момент, и используя условие прочности, подобрать необходимые размеры поперечных сечений. Материал – сталь, допускаемое напряжение изгиба 160 МПа. Сечение – швеллер.
| Вариант | F1, кН | F2, кН | m, кН | а, м |
| 23 | 17 | 18 | 5 | 0,5 |
 рис. 1
рис. 1
Решение
1. Определить реакции в опорах балки
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
Для построения эпюры поперечных сил и изгибающих моментов, провести расчет по характерным точкам
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
Построение эпюры поперечных сил и изгибающих моментов

Подобрать необходимые размеры поперечных сечений
Условие прочности при изгибе:
 ,
,
откуда

____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
Практическая работа №15
Построение эпюр поперечных сил и изгибающих моментов.
Расчеты на прочность
Задача
Для двухопорной балки (рис. 1), нагруженной сосредоточенными силами и парой сил с моментом, определить реакции в опорах, построить эпюры поперечных сил и изгибающих моментов. Найти максимальный момент, и используя условие прочности, подобрать необходимые размеры поперечных сечений. Материал – сталь, допускаемое напряжение изгиба 160 МПа. Сечение – швеллер.
| Вариант | F1, кН | F2, кН | m, кН | а, м |
| 24 | 18 | 22,8 | 4 | 0,6 |
 рис. 1
рис. 1
Решение
1. Определить реакции в опорах балки
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
Для построения эпюры поперечных сил и изгибающих моментов, провести расчет по характерным точкам
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
Построение эпюры поперечных сил и изгибающих моментов

Подобрать необходимые размеры поперечных сечений
Условие прочности при изгибе:
 ,
,
откуда

____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
Практическая работа №15
Построение эпюр поперечных сил и изгибающих моментов.
Расчеты на прочность
Задача
Для двухопорной балки (рис. 1), нагруженной сосредоточенными силами и парой сил с моментом, определить реакции в опорах, построить эпюры поперечных сил и изгибающих моментов. Найти максимальный момент, и используя условие прочности, подобрать необходимые размеры поперечных сечений. Материал – сталь, допускаемое напряжение изгиба 160 МПа. Сечение – швеллер.
| Вариант | F1, кН | F2, кН | m, кН | а, м |
| 25 | 19 | 24 | 3 | 0,6 |
 рис. 1
рис. 1
Решение
1. Определить реакции в опорах балки
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
Для построения эпюры поперечных сил и изгибающих моментов, провести расчет по характерным точкам
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
Построение эпюры поперечных сил и изгибающих моментов

Подобрать необходимые размеры поперечных сечений
Условие прочности при изгибе:
 ,
,
откуда

____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
Просмотр содержимого документа
«Практическая работа №16»
Практическая работа №16
Расчет бруса круглого поперечного сечения
при сочетании основных деформаций
Задача
Для промежуточного вала редуктора (рис. 1), передающего мощность Р при угловой скорости  , определить вертикальную и горизонтальную составляющие реакций подшипников, построить эпюры крутящего момента и изгибающих моментов в вертикальной и горизонтальной плоскостях. Определить диаметр вала, приняв [
, определить вертикальную и горизонтальную составляющие реакций подшипников, построить эпюры крутящего момента и изгибающих моментов в вертикальной и горизонтальной плоскостях. Определить диаметр вала, приняв [ ]=60 МПа и полагая
]=60 МПа и полагая  . Расчет произвести по гипотезе максимальных касательных напряжений.
. Расчет произвести по гипотезе максимальных касательных напряжений.
| Вариант | Р, кВт |
| а, мм | d1, мм | d2, мм |
| 1 | 40 | 70 | 60 | 60 | 250 |
 рис. 1
рис. 1
Решение
1. Определить окружную и радиальную силу
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
2. Определить крутящий момент на валу _______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Определить изгибающий момент в двух плоскостях
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
_____________________________________________________________________________________
_____________________________________________________________________________________
Определить суммарные изгибающие моменты
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
Определить эквивалентный момент по третьей теории прочности
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Определить диаметр вала круглого поперечного сечения из условия прочности
 ,
,
откуда

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Округляем полученную величину:______________________________
Практическая работа №16
Расчет бруса круглого поперечного сечения
при сочетании основных деформаций
Задача
Для промежуточного вала редуктора (рис. 1), передающего мощность Р при угловой скорости  , определить вертикальную и горизонтальную составляющие реакций подшипников, построить эпюры крутящего момента и изгибающих моментов в вертикальной и горизонтальной плоскостях. Определить диаметр вала, приняв [
, определить вертикальную и горизонтальную составляющие реакций подшипников, построить эпюры крутящего момента и изгибающих моментов в вертикальной и горизонтальной плоскостях. Определить диаметр вала, приняв [ ]=60 МПа и полагая
]=60 МПа и полагая  . Расчет произвести по гипотезе максимальных касательных напряжений.
. Расчет произвести по гипотезе максимальных касательных напряжений.
| Вариант | Р, кВт |
| а, мм | d1, мм | d2, мм |
| 2 | 38 | 65 | 70 | 70 | 240 |
 рис. 1
рис. 1
Решение
1. Определить окружную и радиальную силу
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
2. Определить крутящий момент на валу _______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Определить изгибающий момент в двух плоскостях
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
_____________________________________________________________________________________
_____________________________________________________________________________________
Определить суммарные изгибающие моменты
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
Определить эквивалентный момент по третьей теории прочности
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Определить диаметр вала круглого поперечного сечения из условия прочности
 ,
,
откуда

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Округляем полученную величину:______________________________
Практическая работа №16
Расчет бруса круглого поперечного сечения
при сочетании основных деформаций
Задача
Для промежуточного вала редуктора (рис. 1), передающего мощность Р при угловой скорости  , определить вертикальную и горизонтальную составляющие реакций подшипников, построить эпюры крутящего момента и изгибающих моментов в вертикальной и горизонтальной плоскостях. Определить диаметр вала, приняв [
, определить вертикальную и горизонтальную составляющие реакций подшипников, построить эпюры крутящего момента и изгибающих моментов в вертикальной и горизонтальной плоскостях. Определить диаметр вала, приняв [ ]=60 МПа и полагая
]=60 МПа и полагая  . Расчет произвести по гипотезе максимальных касательных напряжений.
. Расчет произвести по гипотезе максимальных касательных напряжений.
| Вариант | Р, кВт |
| а, мм | d1, мм | d2, мм |
| 3 | 36 | 62 | 80 | 80 | 230 |
 рис. 1
рис. 1
Решение
1. Определить окружную и радиальную силу
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
2. Определить крутящий момент на валу _______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Определить изгибающий момент в двух плоскостях
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
_____________________________________________________________________________________
_____________________________________________________________________________________
Определить суммарные изгибающие моменты
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
Определить эквивалентный момент по третьей теории прочности
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Определить диаметр вала круглого поперечного сечения из условия прочности
 ,
,
откуда

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Округляем полученную величину:______________________________
Практическая работа №16
Расчет бруса круглого поперечного сечения
при сочетании основных деформаций
Задача
Для промежуточного вала редуктора (рис. 1), передающего мощность Р при угловой скорости  , определить вертикальную и горизонтальную составляющие реакций подшипников, построить эпюры крутящего момента и изгибающих моментов в вертикальной и горизонтальной плоскостях. Определить диаметр вала, приняв [
, определить вертикальную и горизонтальную составляющие реакций подшипников, построить эпюры крутящего момента и изгибающих моментов в вертикальной и горизонтальной плоскостях. Определить диаметр вала, приняв [ ]=60 МПа и полагая
]=60 МПа и полагая  . Расчет произвести по гипотезе максимальных касательных напряжений.
. Расчет произвести по гипотезе максимальных касательных напряжений.
| Вариант | Р, кВт |
| а, мм | d1, мм | d2, мм |
| 4 | 34 | 58 | 90 | 90 | 220 |
 рис. 1
рис. 1
Решение
1. Определить окружную и радиальную силу
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
2. Определить крутящий момент на валу _______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Определить изгибающий момент в двух плоскостях
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
_____________________________________________________________________________________
_____________________________________________________________________________________
Определить суммарные изгибающие моменты
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
Определить эквивалентный момент по третьей теории прочности
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Определить диаметр вала круглого поперечного сечения из условия прочности
 ,
,
откуда

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Округляем полученную величину:______________________________
Практическая работа №16
Расчет бруса круглого поперечного сечения
при сочетании основных деформаций
Задача
Для промежуточного вала редуктора (рис. 1), передающего мощность Р при угловой скорости  , определить вертикальную и горизонтальную составляющие реакций подшипников, построить эпюры крутящего момента и изгибающих моментов в вертикальной и горизонтальной плоскостях. Определить диаметр вала, приняв [
, определить вертикальную и горизонтальную составляющие реакций подшипников, построить эпюры крутящего момента и изгибающих моментов в вертикальной и горизонтальной плоскостях. Определить диаметр вала, приняв [ ]=60 МПа и полагая
]=60 МПа и полагая  . Расчет произвести по гипотезе максимальных касательных напряжений.
. Расчет произвести по гипотезе максимальных касательных напряжений.
| Вариант | Р, кВт |
| а, мм | d1, мм | d2, мм |
| 5 | 32 | 64 | 100 | 100 | 210 |
 рис. 1
рис. 1
Решение
1. Определить окружную и радиальную силу
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
2. Определить крутящий момент на валу _______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Определить изгибающий момент в двух плоскостях
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
_____________________________________________________________________________________
_____________________________________________________________________________________
Определить суммарные изгибающие моменты
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
Определить эквивалентный момент по третьей теории прочности
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Определить диаметр вала круглого поперечного сечения из условия прочности
 ,
,
откуда

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Округляем полученную величину:______________________________
Практическая работа №16
Расчет бруса круглого поперечного сечения
при сочетании основных деформаций
Задача
Для промежуточного вала редуктора (рис. 1), передающего мощность Р при угловой скорости  , определить вертикальную и горизонтальную составляющие реакций подшипников, построить эпюры крутящего момента и изгибающих моментов в вертикальной и горизонтальной плоскостях. Определить диаметр вала, приняв [
, определить вертикальную и горизонтальную составляющие реакций подшипников, построить эпюры крутящего момента и изгибающих моментов в вертикальной и горизонтальной плоскостях. Определить диаметр вала, приняв [ ]=60 МПа и полагая
]=60 МПа и полагая  . Расчет произвести по гипотезе максимальных касательных напряжений.
. Расчет произвести по гипотезе максимальных касательных напряжений.
| Вариант | Р, кВт |
| а, мм | d1, мм | d2, мм |
| 6 | 30 | 50 | 60 | 110 | 200 |
 рис. 1
рис. 1
Решение
1. Определить окружную и радиальную силу
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
2. Определить крутящий момент на валу _______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Определить изгибающий момент в двух плоскостях
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
_____________________________________________________________________________________
_____________________________________________________________________________________
Определить суммарные изгибающие моменты
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
Определить эквивалентный момент по третьей теории прочности
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Определить диаметр вала круглого поперечного сечения из условия прочности
 ,
,
откуда

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Округляем полученную величину:______________________________
Практическая работа №16
Расчет бруса круглого поперечного сечения
при сочетании основных деформаций
Задача
Для промежуточного вала редуктора (рис. 1), передающего мощность Р при угловой скорости  , определить вертикальную и горизонтальную составляющие реакций подшипников, построить эпюры крутящего момента и изгибающих моментов в вертикальной и горизонтальной плоскостях. Определить диаметр вала, приняв [
, определить вертикальную и горизонтальную составляющие реакций подшипников, построить эпюры крутящего момента и изгибающих моментов в вертикальной и горизонтальной плоскостях. Определить диаметр вала, приняв [ ]=60 МПа и полагая
]=60 МПа и полагая  . Расчет произвести по гипотезе максимальных касательных напряжений.
. Расчет произвести по гипотезе максимальных касательных напряжений.
| Вариант | Р, кВт |
| а, мм | d1, мм | d2, мм |
| 7 | 28 | 46 | 70 | 120 | 190 |
 рис. 1
рис. 1
Решение
1. Определить окружную и радиальную силу
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
2. Определить крутящий момент на валу _______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Определить изгибающий момент в двух плоскостях
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
_____________________________________________________________________________________
_____________________________________________________________________________________
Определить суммарные изгибающие моменты
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
Определить эквивалентный момент по третьей теории прочности
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Определить диаметр вала круглого поперечного сечения из условия прочности
 ,
,
откуда

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Округляем полученную величину:______________________________
Практическая работа №16
Расчет бруса круглого поперечного сечения
при сочетании основных деформаций
Задача
Для промежуточного вала редуктора (рис. 1), передающего мощность Р при угловой скорости  , определить вертикальную и горизонтальную составляющие реакций подшипников, построить эпюры крутящего момента и изгибающих моментов в вертикальной и горизонтальной плоскостях. Определить диаметр вала, приняв [
, определить вертикальную и горизонтальную составляющие реакций подшипников, построить эпюры крутящего момента и изгибающих моментов в вертикальной и горизонтальной плоскостях. Определить диаметр вала, приняв [ ]=60 МПа и полагая
]=60 МПа и полагая  . Расчет произвести по гипотезе максимальных касательных напряжений.
. Расчет произвести по гипотезе максимальных касательных напряжений.
| Вариант | Р, кВт |
| а, мм | d1, мм | d2, мм |
| 8 | 26 | 42 | 80 | 130 | 180 |
 рис. 1
рис. 1
Решение
1. Определить окружную и радиальную силу
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
2. Определить крутящий момент на валу _______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Определить изгибающий момент в двух плоскостях
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
_____________________________________________________________________________________
_____________________________________________________________________________________
Определить суммарные изгибающие моменты
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
Определить эквивалентный момент по третьей теории прочности
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Определить диаметр вала круглого поперечного сечения из условия прочности
 ,
,
откуда

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Округляем полученную величину:______________________________
Практическая работа №16
Расчет бруса круглого поперечного сечения
при сочетании основных деформаций
Задача
Для промежуточного вала редуктора (рис. 1), передающего мощность Р при угловой скорости  , определить вертикальную и горизонтальную составляющие реакций подшипников, построить эпюры крутящего момента и изгибающих моментов в вертикальной и горизонтальной плоскостях. Определить диаметр вала, приняв [
, определить вертикальную и горизонтальную составляющие реакций подшипников, построить эпюры крутящего момента и изгибающих моментов в вертикальной и горизонтальной плоскостях. Определить диаметр вала, приняв [ ]=60 МПа и полагая
]=60 МПа и полагая  . Расчет произвести по гипотезе максимальных касательных напряжений.
. Расчет произвести по гипотезе максимальных касательных напряжений.
| Вариант | Р, кВт |
| а, мм | d1, мм | d2, мм |
| 9 | 24 | 38 | 90 | 140 | 170 |
 рис. 1
рис. 1
Решение
1. Определить окружную и радиальную силу
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
2. Определить крутящий момент на валу _______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Определить изгибающий момент в двух плоскостях
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
_____________________________________________________________________________________
_____________________________________________________________________________________
Определить суммарные изгибающие моменты
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
Определить эквивалентный момент по третьей теории прочности
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Определить диаметр вала круглого поперечного сечения из условия прочности
 ,
,
откуда

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Округляем полученную величину:______________________________
Практическая работа №16
Расчет бруса круглого поперечного сечения
при сочетании основных деформаций
Задача
Для промежуточного вала редуктора (рис. 1), передающего мощность Р при угловой скорости  , определить вертикальную и горизонтальную составляющие реакций подшипников, построить эпюры крутящего момента и изгибающих моментов в вертикальной и горизонтальной плоскостях. Определить диаметр вала, приняв [
, определить вертикальную и горизонтальную составляющие реакций подшипников, построить эпюры крутящего момента и изгибающих моментов в вертикальной и горизонтальной плоскостях. Определить диаметр вала, приняв [ ]=60 МПа и полагая
]=60 МПа и полагая  . Расчет произвести по гипотезе максимальных касательных напряжений.
. Расчет произвести по гипотезе максимальных касательных напряжений.
| Вариант | Р, кВт |
| а, мм | d1, мм | d2, мм |
| 10 | 22 | 34 | 100 | 150 | 160 |
 рис. 1
рис. 1
Решение
1. Определить окружную и радиальную силу
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
2. Определить крутящий момент на валу _______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Определить изгибающий момент в двух плоскостях
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
_____________________________________________________________________________________
_____________________________________________________________________________________
Определить суммарные изгибающие моменты
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
Определить эквивалентный момент по третьей теории прочности
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Определить диаметр вала круглого поперечного сечения из условия прочности
 ,
,
откуда

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Округляем полученную величину:______________________________
Практическая работа №16
Расчет бруса круглого поперечного сечения
при сочетании основных деформаций
Задача
Для промежуточного вала редуктора (рис. 1), передающего мощность Р при угловой скорости  , определить вертикальную и горизонтальную составляющие реакций подшипников, построить эпюры крутящего момента и изгибающих моментов в вертикальной и горизонтальной плоскостях. Определить диаметр вала, приняв [
, определить вертикальную и горизонтальную составляющие реакций подшипников, построить эпюры крутящего момента и изгибающих моментов в вертикальной и горизонтальной плоскостях. Определить диаметр вала, приняв [ ]=60 МПа и полагая
]=60 МПа и полагая  . Расчет произвести по гипотезе максимальных касательных напряжений.
. Расчет произвести по гипотезе максимальных касательных напряжений.
| Вариант | Р, кВт |
| а, мм | d1, мм | d2, мм |
| 11 | 30 | 50 | 60 | 60 | 140 |
 рис. 1
рис. 1
Решение
1. Определить окружную и радиальную силу
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
2. Определить крутящий момент на валу _______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Определить изгибающий момент в двух плоскостях
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
_____________________________________________________________________________________
_____________________________________________________________________________________
Определить суммарные изгибающие моменты
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
Определить эквивалентный момент по третьей теории прочности
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Определить диаметр вала круглого поперечного сечения из условия прочности
 ,
,
откуда

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Округляем полученную величину:______________________________
Практическая работа №16
Расчет бруса круглого поперечного сечения
при сочетании основных деформаций
Задача
Для промежуточного вала редуктора (рис. 1), передающего мощность Р при угловой скорости  , определить вертикальную и горизонтальную составляющие реакций подшипников, построить эпюры крутящего момента и изгибающих моментов в вертикальной и горизонтальной плоскостях. Определить диаметр вала, приняв [
, определить вертикальную и горизонтальную составляющие реакций подшипников, построить эпюры крутящего момента и изгибающих моментов в вертикальной и горизонтальной плоскостях. Определить диаметр вала, приняв [ ]=60 МПа и полагая
]=60 МПа и полагая  . Расчет произвести по гипотезе максимальных касательных напряжений.
. Расчет произвести по гипотезе максимальных касательных напряжений.
| Вариант | Р, кВт |
| а, мм | d1, мм | d2, мм |
| 12 | 28 | 46 | 70 | 70 | 130 |
 рис. 1
рис. 1
Решение
1. Определить окружную и радиальную силу
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
2. Определить крутящий момент на валу _______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Определить изгибающий момент в двух плоскостях
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
_____________________________________________________________________________________
_____________________________________________________________________________________
Определить суммарные изгибающие моменты
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
Определить эквивалентный момент по третьей теории прочности
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Определить диаметр вала круглого поперечного сечения из условия прочности
 ,
,
откуда

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Округляем полученную величину:______________________________
Практическая работа №16
Расчет бруса круглого поперечного сечения
при сочетании основных деформаций
Задача
Для промежуточного вала редуктора (рис. 1), передающего мощность Р при угловой скорости  , определить вертикальную и горизонтальную составляющие реакций подшипников, построить эпюры крутящего момента и изгибающих моментов в вертикальной и горизонтальной плоскостях. Определить диаметр вала, приняв [
, определить вертикальную и горизонтальную составляющие реакций подшипников, построить эпюры крутящего момента и изгибающих моментов в вертикальной и горизонтальной плоскостях. Определить диаметр вала, приняв [ ]=60 МПа и полагая
]=60 МПа и полагая  . Расчет произвести по гипотезе максимальных касательных напряжений.
. Расчет произвести по гипотезе максимальных касательных напряжений.
| Вариант | Р, кВт |
| а, мм | d1, мм | d2, мм |
| 13 | 26 | 42 | 80 | 80 | 90 |
 рис. 1
рис. 1
Решение
1. Определить окружную и радиальную силу
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
2. Определить крутящий момент на валу _______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Определить изгибающий момент в двух плоскостях
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
_____________________________________________________________________________________
_____________________________________________________________________________________
Определить суммарные изгибающие моменты
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
Определить эквивалентный момент по третьей теории прочности
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Определить диаметр вала круглого поперечного сечения из условия прочности
 ,
,
откуда

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Округляем полученную величину:______________________________
Практическая работа №16
Расчет бруса круглого поперечного сечения
при сочетании основных деформаций
Задача
Для промежуточного вала редуктора (рис. 1), передающего мощность Р при угловой скорости  , определить вертикальную и горизонтальную составляющие реакций подшипников, построить эпюры крутящего момента и изгибающих моментов в вертикальной и горизонтальной плоскостях. Определить диаметр вала, приняв [
, определить вертикальную и горизонтальную составляющие реакций подшипников, построить эпюры крутящего момента и изгибающих моментов в вертикальной и горизонтальной плоскостях. Определить диаметр вала, приняв [ ]=60 МПа и полагая
]=60 МПа и полагая  . Расчет произвести по гипотезе максимальных касательных напряжений.
. Расчет произвести по гипотезе максимальных касательных напряжений.
| Вариант | Р, кВт |
| а, мм | d1, мм | d2, мм |
| 14 | 24 | 38 | 90 | 90 | 80 |
 рис. 1
рис. 1
Решение
1. Определить окружную и радиальную силу
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
2. Определить крутящий момент на валу _______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Определить изгибающий момент в двух плоскостях
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
_____________________________________________________________________________________
_____________________________________________________________________________________
Определить суммарные изгибающие моменты
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
Определить эквивалентный момент по третьей теории прочности
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Определить диаметр вала круглого поперечного сечения из условия прочности
 ,
,
откуда

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Округляем полученную величину:______________________________
Практическая работа №16
Расчет бруса круглого поперечного сечения
при сочетании основных деформаций
Задача
Для промежуточного вала редуктора (рис. 1), передающего мощность Р при угловой скорости  , определить вертикальную и горизонтальную составляющие реакций подшипников, построить эпюры крутящего момента и изгибающих моментов в вертикальной и горизонтальной плоскостях. Определить диаметр вала, приняв [
, определить вертикальную и горизонтальную составляющие реакций подшипников, построить эпюры крутящего момента и изгибающих моментов в вертикальной и горизонтальной плоскостях. Определить диаметр вала, приняв [ ]=60 МПа и полагая
]=60 МПа и полагая  . Расчет произвести по гипотезе максимальных касательных напряжений.
. Расчет произвести по гипотезе максимальных касательных напряжений.
| Вариант | Р, кВт |
| а, мм | d1, мм | d2, мм |
| 15 | 22 | 34 | 50 | 60 | 70 |
 рис. 1
рис. 1
Решение
1. Определить окружную и радиальную силу
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
2. Определить крутящий момент на валу _______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Определить изгибающий момент в двух плоскостях
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
_____________________________________________________________________________________
_____________________________________________________________________________________
Определить суммарные изгибающие моменты
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
Определить эквивалентный момент по третьей теории прочности
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Определить диаметр вала круглого поперечного сечения из условия прочности
 ,
,
откуда

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Округляем полученную величину:______________________________
Практическая работа №16
Расчет бруса круглого поперечного сечения
при сочетании основных деформаций
Задача
Для промежуточного вала редуктора (рис. 1), передающего мощность Р при угловой скорости  , определить вертикальную и горизонтальную составляющие реакций подшипников, построить эпюры крутящего момента и изгибающих моментов в вертикальной и горизонтальной плоскостях. Определить диаметр вала, приняв [
, определить вертикальную и горизонтальную составляющие реакций подшипников, построить эпюры крутящего момента и изгибающих моментов в вертикальной и горизонтальной плоскостях. Определить диаметр вала, приняв [ ]=60 МПа и полагая
]=60 МПа и полагая  . Расчет произвести по гипотезе максимальных касательных напряжений.
. Расчет произвести по гипотезе максимальных касательных напряжений.
| Вариант | Р, кВт |
| а, мм | d1, мм | d2, мм |
| 16 | 22 | 34 | 100 | 100 | 200 |
 рис. 1
рис. 1
Решение
1. Определить окружную и радиальную силу
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
2. Определить крутящий момент на валу _______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Определить изгибающий момент в двух плоскостях
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
_____________________________________________________________________________________
_____________________________________________________________________________________
Определить суммарные изгибающие моменты
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
Определить эквивалентный момент по третьей теории прочности
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Определить диаметр вала круглого поперечного сечения из условия прочности
 ,
,
откуда

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Округляем полученную величину:______________________________
Практическая работа №16
Расчет бруса круглого поперечного сечения
при сочетании основных деформаций
Задача
Для промежуточного вала редуктора (рис. 1), передающего мощность Р при угловой скорости  , определить вертикальную и горизонтальную составляющие реакций подшипников, построить эпюры крутящего момента и изгибающих моментов в вертикальной и горизонтальной плоскостях. Определить диаметр вала, приняв [
, определить вертикальную и горизонтальную составляющие реакций подшипников, построить эпюры крутящего момента и изгибающих моментов в вертикальной и горизонтальной плоскостях. Определить диаметр вала, приняв [ ]=60 МПа и полагая
]=60 МПа и полагая  . Расчет произвести по гипотезе максимальных касательных напряжений.
. Расчет произвести по гипотезе максимальных касательных напряжений.
| Вариант | Р, кВт |
| а, мм | d1, мм | d2, мм |
| 17 | 30 | 50 | 60 | 110 | 190 |
 рис. 1
рис. 1
Решение
1. Определить окружную и радиальную силу
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
2. Определить крутящий момент на валу _______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Определить изгибающий момент в двух плоскостях
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
_____________________________________________________________________________________
_____________________________________________________________________________________
Определить суммарные изгибающие моменты
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
Определить эквивалентный момент по третьей теории прочности
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Определить диаметр вала круглого поперечного сечения из условия прочности
 ,
,
откуда

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Округляем полученную величину:______________________________
Практическая работа №16
Расчет бруса круглого поперечного сечения
при сочетании основных деформаций
Задача
Для промежуточного вала редуктора (рис. 1), передающего мощность Р при угловой скорости  , определить вертикальную и горизонтальную составляющие реакций подшипников, построить эпюры крутящего момента и изгибающих моментов в вертикальной и горизонтальной плоскостях. Определить диаметр вала, приняв [
, определить вертикальную и горизонтальную составляющие реакций подшипников, построить эпюры крутящего момента и изгибающих моментов в вертикальной и горизонтальной плоскостях. Определить диаметр вала, приняв [ ]=60 МПа и полагая
]=60 МПа и полагая  . Расчет произвести по гипотезе максимальных касательных напряжений.
. Расчет произвести по гипотезе максимальных касательных напряжений.
| Вариант | Р, кВт |
| а, мм | d1, мм | d2, мм |
| 18 | 28 | 46 | 70 | 120 | 180 |
 рис. 1
рис. 1
Решение
1. Определить окружную и радиальную силу
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
2. Определить крутящий момент на валу _______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Определить изгибающий момент в двух плоскостях
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
_____________________________________________________________________________________
_____________________________________________________________________________________
Определить суммарные изгибающие моменты
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
Определить эквивалентный момент по третьей теории прочности
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Определить диаметр вала круглого поперечного сечения из условия прочности
 ,
,
откуда

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Округляем полученную величину:______________________________
Практическая работа №16
Расчет бруса круглого поперечного сечения
при сочетании основных деформаций
Задача
Для промежуточного вала редуктора (рис. 1), передающего мощность Р при угловой скорости  , определить вертикальную и горизонтальную составляющие реакций подшипников, построить эпюры крутящего момента и изгибающих моментов в вертикальной и горизонтальной плоскостях. Определить диаметр вала, приняв [
, определить вертикальную и горизонтальную составляющие реакций подшипников, построить эпюры крутящего момента и изгибающих моментов в вертикальной и горизонтальной плоскостях. Определить диаметр вала, приняв [ ]=60 МПа и полагая
]=60 МПа и полагая  . Расчет произвести по гипотезе максимальных касательных напряжений.
. Расчет произвести по гипотезе максимальных касательных напряжений.
| Вариант | Р, кВт |
| а, мм | d1, мм | d2, мм |
| 19 | 26 | 42 | 80 | 130 | 170 |
 рис. 1
рис. 1
Решение
1. Определить окружную и радиальную силу
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
2. Определить крутящий момент на валу _______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Определить изгибающий момент в двух плоскостях
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
_____________________________________________________________________________________
_____________________________________________________________________________________
Определить суммарные изгибающие моменты
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
Определить эквивалентный момент по третьей теории прочности
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Определить диаметр вала круглого поперечного сечения из условия прочности
 ,
,
откуда

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Округляем полученную величину:______________________________
Практическая работа №16
Расчет бруса круглого поперечного сечения
при сочетании основных деформаций
Задача
Для промежуточного вала редуктора (рис. 1), передающего мощность Р при угловой скорости  , определить вертикальную и горизонтальную составляющие реакций подшипников, построить эпюры крутящего момента и изгибающих моментов в вертикальной и горизонтальной плоскостях. Определить диаметр вала, приняв [
, определить вертикальную и горизонтальную составляющие реакций подшипников, построить эпюры крутящего момента и изгибающих моментов в вертикальной и горизонтальной плоскостях. Определить диаметр вала, приняв [ ]=60 МПа и полагая
]=60 МПа и полагая  . Расчет произвести по гипотезе максимальных касательных напряжений.
. Расчет произвести по гипотезе максимальных касательных напряжений.
| Вариант | Р, кВт |
| а, мм | d1, мм | d2, мм |
| 20 | 24 | 38 | 90 | 140 | 160 |
 рис. 1
рис. 1
Решение
1. Определить окружную и радиальную силу
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
2. Определить крутящий момент на валу _______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Определить изгибающий момент в двух плоскостях
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
_____________________________________________________________________________________
_____________________________________________________________________________________
Определить суммарные изгибающие моменты
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
Определить эквивалентный момент по третьей теории прочности
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Определить диаметр вала круглого поперечного сечения из условия прочности
 ,
,
откуда

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Округляем полученную величину:______________________________
Практическая работа №16
Расчет бруса круглого поперечного сечения
при сочетании основных деформаций
Задача
Для промежуточного вала редуктора (рис. 1), передающего мощность Р при угловой скорости  , определить вертикальную и горизонтальную составляющие реакций подшипников, построить эпюры крутящего момента и изгибающих моментов в вертикальной и горизонтальной плоскостях. Определить диаметр вала, приняв [
, определить вертикальную и горизонтальную составляющие реакций подшипников, построить эпюры крутящего момента и изгибающих моментов в вертикальной и горизонтальной плоскостях. Определить диаметр вала, приняв [ ]=60 МПа и полагая
]=60 МПа и полагая  . Расчет произвести по гипотезе максимальных касательных напряжений.
. Расчет произвести по гипотезе максимальных касательных напряжений.
| Вариант | Р, кВт |
| а, мм | d1, мм | d2, мм |
| 21 | 22 | 34 | 100 | 100 | 150 |
 рис. 1
рис. 1
Решение
1. Определить окружную и радиальную силу
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
2. Определить крутящий момент на валу _______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Определить изгибающий момент в двух плоскостях
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
_____________________________________________________________________________________
_____________________________________________________________________________________
Определить суммарные изгибающие моменты
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
Определить эквивалентный момент по третьей теории прочности
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Определить диаметр вала круглого поперечного сечения из условия прочности
 ,
,
откуда

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Округляем полученную величину:______________________________
Практическая работа №16
Расчет бруса круглого поперечного сечения
при сочетании основных деформаций
Задача
Для промежуточного вала редуктора (рис. 1), передающего мощность Р при угловой скорости  , определить вертикальную и горизонтальную составляющие реакций подшипников, построить эпюры крутящего момента и изгибающих моментов в вертикальной и горизонтальной плоскостях. Определить диаметр вала, приняв [
, определить вертикальную и горизонтальную составляющие реакций подшипников, построить эпюры крутящего момента и изгибающих моментов в вертикальной и горизонтальной плоскостях. Определить диаметр вала, приняв [ ]=60 МПа и полагая
]=60 МПа и полагая  . Расчет произвести по гипотезе максимальных касательных напряжений.
. Расчет произвести по гипотезе максимальных касательных напряжений.
| Вариант | Р, кВт |
| а, мм | d1, мм | d2, мм |
| 22 | 26 | 42 | 90 | 90 | 80 |
 рис. 1
рис. 1
Решение
1. Определить окружную и радиальную силу
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
2. Определить крутящий момент на валу _______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Определить изгибающий момент в двух плоскостях
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
_____________________________________________________________________________________
_____________________________________________________________________________________
Определить суммарные изгибающие моменты
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
Определить эквивалентный момент по третьей теории прочности
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Определить диаметр вала круглого поперечного сечения из условия прочности
 ,
,
откуда

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Округляем полученную величину:______________________________
Практическая работа №16
Расчет бруса круглого поперечного сечения
при сочетании основных деформаций
Задача
Для промежуточного вала редуктора (рис. 1), передающего мощность Р при угловой скорости  , определить вертикальную и горизонтальную составляющие реакций подшипников, построить эпюры крутящего момента и изгибающих моментов в вертикальной и горизонтальной плоскостях. Определить диаметр вала, приняв [
, определить вертикальную и горизонтальную составляющие реакций подшипников, построить эпюры крутящего момента и изгибающих моментов в вертикальной и горизонтальной плоскостях. Определить диаметр вала, приняв [ ]=60 МПа и полагая
]=60 МПа и полагая  . Расчет произвести по гипотезе максимальных касательных напряжений.
. Расчет произвести по гипотезе максимальных касательных напряжений.
| Вариант | Р, кВт |
| а, мм | d1, мм | d2, мм |
| 23 | 40 | 70 | 70 | 120 | 180 |
 рис. 1
рис. 1
Решение
1. Определить окружную и радиальную силу
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
2. Определить крутящий момент на валу _______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Определить изгибающий момент в двух плоскостях
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
_____________________________________________________________________________________
_____________________________________________________________________________________
Определить суммарные изгибающие моменты
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
Определить эквивалентный момент по третьей теории прочности
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Определить диаметр вала круглого поперечного сечения из условия прочности
 ,
,
откуда

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Округляем полученную величину:______________________________
Практическая работа №16
Расчет бруса круглого поперечного сечения
при сочетании основных деформаций
Задача
Для промежуточного вала редуктора (рис. 1), передающего мощность Р при угловой скорости  , определить вертикальную и горизонтальную составляющие реакций подшипников, построить эпюры крутящего момента и изгибающих моментов в вертикальной и горизонтальной плоскостях. Определить диаметр вала, приняв [
, определить вертикальную и горизонтальную составляющие реакций подшипников, построить эпюры крутящего момента и изгибающих моментов в вертикальной и горизонтальной плоскостях. Определить диаметр вала, приняв [ ]=60 МПа и полагая
]=60 МПа и полагая  . Расчет произвести по гипотезе максимальных касательных напряжений.
. Расчет произвести по гипотезе максимальных касательных напряжений.
| Вариант | Р, кВт |
| а, мм | d1, мм | d2, мм |
| 24 | 38 | 65 | 80 | 130 | 170 |
 рис. 1
рис. 1
Решение
1. Определить окружную и радиальную силу
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
2. Определить крутящий момент на валу _______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Определить изгибающий момент в двух плоскостях
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
_____________________________________________________________________________________
_____________________________________________________________________________________
Определить суммарные изгибающие моменты
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
Определить эквивалентный момент по третьей теории прочности
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Определить диаметр вала круглого поперечного сечения из условия прочности
 ,
,
откуда

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Округляем полученную величину:______________________________
Практическая работа №16
Расчет бруса круглого поперечного сечения
при сочетании основных деформаций
Задача
Для промежуточного вала редуктора (рис. 1), передающего мощность Р при угловой скорости  , определить вертикальную и горизонтальную составляющие реакций подшипников, построить эпюры крутящего момента и изгибающих моментов в вертикальной и горизонтальной плоскостях. Определить диаметр вала, приняв [
, определить вертикальную и горизонтальную составляющие реакций подшипников, построить эпюры крутящего момента и изгибающих моментов в вертикальной и горизонтальной плоскостях. Определить диаметр вала, приняв [ ]=60 МПа и полагая
]=60 МПа и полагая  . Расчет произвести по гипотезе максимальных касательных напряжений.
. Расчет произвести по гипотезе максимальных касательных напряжений.
| Вариант | Р, кВт |
| а, мм | d1, мм | d2, мм |
| 25 | 36 | 62 | 90 | 140 | 160 |
 рис. 1
рис. 1
Решение
1. Определить окружную и радиальную силу
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
2. Определить крутящий момент на валу _______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Определить изгибающий момент в двух плоскостях
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
_____________________________________________________________________________________
_____________________________________________________________________________________
Определить суммарные изгибающие моменты
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
Определить эквивалентный момент по третьей теории прочности
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Определить диаметр вала круглого поперечного сечения из условия прочности
 ,
,
откуда

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Округляем полученную величину:______________________________
Просмотр содержимого документа
«Практическая работа №17»
Практическая работа №17
Устойчивость сжатых стержней. Расчеты на устойчивость
Вариант №1
Задача №1
Рассчитать гибкость стержня (l=1,5м). Круглый стержень диаметром 24мм закреплен так, как показано на рис. 1.
 рис. 1
рис. 1
Решение
Гибкость стержня определяется по формуле:

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Определяем минимальный радиус инерции для круга:

_____________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
Коэффициент приведения длины для данной схемы крепления:

Задача №2
Проверить устойчивость стержня. Стержень длиной 1 м защемлен одним концом, сечение – швеллер №16, материал – Ст. 3, запас устойчивости трехкратный. Стержень нагружен сжимающей силой F=82 кН (рис. 2).
 рис. 2
рис. 2
Решение
1. Определяем основные геометрические параметры сечения стержня по ГОСТ 8240-89.
Швеллер №___: А=_____см2, Iу=_____см4, iу=_____см.
2. Определяем категорию стержня в зависимости от гибкости.
Предельная гибкость для материала _________ составляет  =_____.
=_____.
Расчетная гибкость:

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Расчет Fкр ведем по формуле Эйлера:

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
3. Допускаемая нагрузка на стержень:

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
4. Условие устойчивости:

_______________________. Устойчивость стержня ____________.
Практическая работа №17
Устойчивость сжатых стержней. Расчеты на устойчивость
Вариант №2
Задача №1
Рассчитать гибкость стержня (l=1м). Круглый стержень диаметром 26мм закреплен так, как показано на рис. 1.
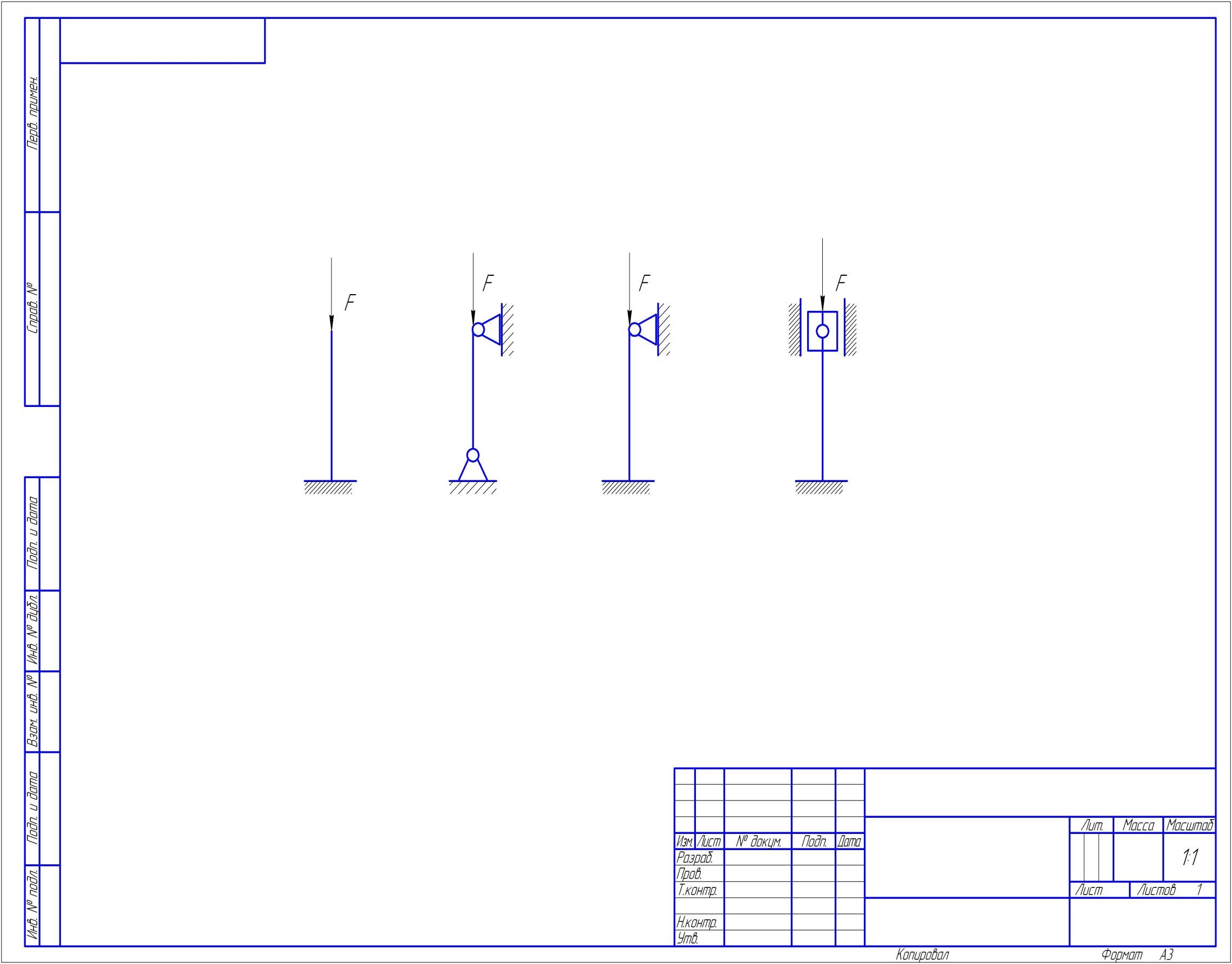 рис. 1
рис. 1
Решение
Гибкость стержня определяется по формуле:

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Определяем минимальный радиус инерции для круга:

_____________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
Коэффициент приведения длины для данной схемы крепления:

Задача №2
Проверить устойчивость стержня. Стержень длиной 1 м закреплен так, как показано на рис. 2, сечение – швеллер №14, материал – Ст. 2, запас устойчивости трехкратный. Стержень нагружен сжимающей силой F=80 кН (рис. 2).
 рис. 2
рис. 2
Решение
1. Определяем основные геометрические параметры сечения стержня по ГОСТ 8240-89.
Швеллер №___: А=_____см2, Iу=_____см4, iу=_____см.
2. Определяем категорию стержня в зависимости от гибкости.
Предельная гибкость для материала _________ составляет  =_____.
=_____.
Расчетная гибкость:

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Расчет Fкр ведем по формуле Эйлера:

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
3. Допускаемая нагрузка на стержень:

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
4. Условие устойчивости:

_______________________. Устойчивость стержня ____________.
Практическая работа №17
Устойчивость сжатых стержней. Расчеты на устойчивость
Вариант №3
Задача №1
Рассчитать гибкость стержня (l=1,5м). Круглый стержень диаметром 20мм закреплен так, как показано на рис. 1.
 рис. 1
рис. 1
Решение
Гибкость стержня определяется по формуле:

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Определяем минимальный радиус инерции для круга:

_____________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
Коэффициент приведения длины для данной схемы крепления:

Задача №2
Проверить устойчивость стержня. Стержень длиной 1 м закреплен так, как показано на рис. 2, сечение – швеллер №18, материал – Ст. 20, запас устойчивости трехкратный. Стержень нагружен сжимающей силой F=94 кН (рис. 2).
 рис. 2
рис. 2
Решение
1. Определяем основные геометрические параметры сечения стержня по ГОСТ 8240-89.
Швеллер №___: А=_____см2, Iу=_____см4, iу=_____см.
2. Определяем категорию стержня в зависимости от гибкости.
Предельная гибкость для материала _________ составляет  =_____.
=_____.
Расчетная гибкость:

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Расчет Fкр ведем по формуле Эйлера:

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
3. Допускаемая нагрузка на стержень:

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
4. Условие устойчивости:

_______________________. Устойчивость стержня ____________.
Практическая работа №17
Устойчивость сжатых стержней. Расчеты на устойчивость
Вариант №4
Задача №1
Рассчитать гибкость стержня (l=1,8м). Круглый стержень диаметром 28мм закреплен так, как показано на рис. 1.
 рис. 1
рис. 1
Решение
Гибкость стержня определяется по формуле:

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Определяем минимальный радиус инерции для круга:

_____________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
Коэффициент приведения длины для данной схемы крепления:

Задача №2
Проверить устойчивость стержня. Стержень длиной 1 м закреплен так, как показано на рис. 2, сечение – швеллер №20, материал – Ст. 3, запас устойчивости трехкратный. Стержень нагружен сжимающей силой F=96 кН (рис. 2).
 рис. 2
рис. 2
Решение
1. Определяем основные геометрические параметры сечения стержня по ГОСТ 8240-89.
Швеллер №___: А=_____см2, Iу=_____см4, iу=_____см.
2. Определяем категорию стержня в зависимости от гибкости.
Предельная гибкость для материала _________ составляет  =_____.
=_____.
Расчетная гибкость:

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Расчет Fкр ведем по формуле Эйлера:

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
3. Допускаемая нагрузка на стержень:

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
4. Условие устойчивости:

_______________________. Устойчивость стержня ____________.
Практическая работа №17
Устойчивость сжатых стержней. Расчеты на устойчивость
Вариант №5
Задача №1
Рассчитать гибкость стержня (l=1,0м). Круглый стержень диаметром 18мм закреплен так, как показано на рис. 1.
 рис. 1
рис. 1
Решение
Гибкость стержня определяется по формуле:

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Определяем минимальный радиус инерции для круга:

_____________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
Коэффициент приведения длины для данной схемы крепления:

Задача №2
Проверить устойчивость стержня. Стержень длиной 1 м защемлен одним концом, сечение – швеллер №22, материал – Ст. 2, запас устойчивости трехкратный. Стержень нагружен сжимающей силой F=100 кН (рис. 2).
 рис. 2
рис. 2
Решение
1. Определяем основные геометрические параметры сечения стержня по ГОСТ 8240-89.
Швеллер №___: А=_____см2, Iу=_____см4, iу=_____см.
2. Определяем категорию стержня в зависимости от гибкости.
Предельная гибкость для материала _________ составляет  =_____.
=_____.
Расчетная гибкость:

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Расчет Fкр ведем по формуле Эйлера:

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
3. Допускаемая нагрузка на стержень:

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
4. Условие устойчивости:

_______________________. Устойчивость стержня ____________.
Практическая работа №17
Устойчивость сжатых стержней. Расчеты на устойчивость
Вариант №6
Задача №1
Рассчитать гибкость стержня (l=1м). Круглый стержень диаметром 30мм закреплен так, как показано на рис. 1.
 рис. 1
рис. 1
Решение
Гибкость стержня определяется по формуле:

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Определяем минимальный радиус инерции для круга:

_____________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
Коэффициент приведения длины для данной схемы крепления:

Задача №2
Проверить устойчивость стержня. Стержень длиной 1 м закреплен так, как показано на рис. 2, сечение – швеллер №14, материал – Ст. 20, запас устойчивости трехкратный. Стержень нагружен сжимающей силой F=88 кН (рис. 2).
 рис. 2
рис. 2
Решение
1. Определяем основные геометрические параметры сечения стержня по ГОСТ 8240-89.
Швеллер №___: А=_____см2, Iу=_____см4, iу=_____см.
2. Определяем категорию стержня в зависимости от гибкости.
Предельная гибкость для материала _________ составляет  =_____.
=_____.
Расчетная гибкость:

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Расчет Fкр ведем по формуле Эйлера:

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
3. Допускаемая нагрузка на стержень:

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
4. Условие устойчивости:

_______________________. Устойчивость стержня ____________.
Практическая работа №17
Устойчивость сжатых стержней. Расчеты на устойчивость
Вариант №7
Задача №1
Рассчитать гибкость стержня (l=1,5м). Круглый стержень диаметром 28мм закреплен так, как показано на рис. 1.
 рис. 1
рис. 1
Решение
Гибкость стержня определяется по формуле:

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Определяем минимальный радиус инерции для круга:

_____________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
Коэффициент приведения длины для данной схемы крепления:

Задача №2
Проверить устойчивость стержня. Стержень длиной 1 м закреплен так, как показано на рис. 2, сечение – швеллер №22, материал – Ст. 3, запас устойчивости трехкратный. Стержень нагружен сжимающей силой F=90 кН (рис. 2).
 рис. 2
рис. 2
Решение
1. Определяем основные геометрические параметры сечения стержня по ГОСТ 8240-89.
Швеллер №___: А=_____см2, Iу=_____см4, iу=_____см.
2. Определяем категорию стержня в зависимости от гибкости.
Предельная гибкость для материала _________ составляет  =_____.
=_____.
Расчетная гибкость:

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Расчет Fкр ведем по формуле Эйлера:

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
3. Допускаемая нагрузка на стержень:

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
4. Условие устойчивости:

_______________________. Устойчивость стержня ____________.
Практическая работа №17
Устойчивость сжатых стержней. Расчеты на устойчивость
Вариант №8
Задача №1
Рассчитать гибкость стержня (l=1,8м). Круглый стержень диаметром 20мм закреплен так, как показано на рис. 1.
 рис. 1
рис. 1
Решение
Гибкость стержня определяется по формуле:

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Определяем минимальный радиус инерции для круга:

_____________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
Коэффициент приведения длины для данной схемы крепления:

Задача №2
Проверить устойчивость стержня. Стержень длиной 1 м закреплен так, как показано на рис. 2, сечение – швеллер №22, материал – Ст. 2, запас устойчивости трехкратный. Стержень нагружен сжимающей силой F=100 кН (рис. 2).
 рис. 2
рис. 2
Решение
1. Определяем основные геометрические параметры сечения стержня по ГОСТ 8240-89.
Швеллер №___: А=_____см2, Iу=_____см4, iу=_____см.
2. Определяем категорию стержня в зависимости от гибкости.
Предельная гибкость для материала _________ составляет  =_____.
=_____.
Расчетная гибкость:

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Расчет Fкр ведем по формуле Эйлера:

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
3. Допускаемая нагрузка на стержень:

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
4. Условие устойчивости:

_______________________. Устойчивость стержня ____________.
Практическая работа №17
Устойчивость сжатых стержней. Расчеты на устойчивость
Вариант №9
Задача №1
Рассчитать гибкость стержня (l=1,0м). Круглый стержень диаметром 26мм закреплен так, как показано на рис. 1.
 рис. 1
рис. 1
Решение
Гибкость стержня определяется по формуле:

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Определяем минимальный радиус инерции для круга:

_____________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
Коэффициент приведения длины для данной схемы крепления:

Задача №2
Проверить устойчивость стержня. Стержень длиной 1 м защемлен одним концом, сечение – швеллер №14, материал – Ст. 20, запас устойчивости трехкратный. Стержень нагружен сжимающей силой F=94 кН (рис. 2).
 рис. 2
рис. 2
Решение
1. Определяем основные геометрические параметры сечения стержня по ГОСТ 8240-89.
Швеллер №___: А=_____см2, Iу=_____см4, iу=_____см.
2. Определяем категорию стержня в зависимости от гибкости.
Предельная гибкость для материала _________ составляет  =_____.
=_____.
Расчетная гибкость:

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Расчет Fкр ведем по формуле Эйлера:

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
3. Допускаемая нагрузка на стержень:

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
4. Условие устойчивости:

_______________________. Устойчивость стержня ____________.
Практическая работа №17
Устойчивость сжатых стержней. Расчеты на устойчивость
Вариант №10
Задача №1
Рассчитать гибкость стержня (l=1,5м). Круглый стержень диаметром 28мм закреплен так, как показано на рис. 1.
 рис. 1
рис. 1
Решение
Гибкость стержня определяется по формуле:

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Определяем минимальный радиус инерции для круга:

_____________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
Коэффициент приведения длины для данной схемы крепления:

Задача №2
Проверить устойчивость стержня. Стержень длиной 1 м закреплен так, как показано на рис. 2, сечение – швеллер №24, материал – Ст. 3, запас устойчивости трехкратный. Стержень нагружен сжимающей силой F=100 кН (рис. 2).
 рис. 2
рис. 2
Решение
1. Определяем основные геометрические параметры сечения стержня по ГОСТ 8240-89.
Швеллер №___: А=_____см2, Iу=_____см4, iу=_____см.
2. Определяем категорию стержня в зависимости от гибкости.
Предельная гибкость для материала _________ составляет  =_____.
=_____.
Расчетная гибкость:

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Расчет Fкр ведем по формуле Эйлера:

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
3. Допускаемая нагрузка на стержень:

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
4. Условие устойчивости:

_______________________. Устойчивость стержня ____________.
Практическая работа №17
Устойчивость сжатых стержней. Расчеты на устойчивость
Вариант №11
Задача №1
Рассчитать гибкость стержня (l=1,8м). Круглый стержень диаметром 26мм закреплен так, как показано на рис. 1.
 рис. 1
рис. 1
Решение
Гибкость стержня определяется по формуле:

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Определяем минимальный радиус инерции для круга:

_____________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
Коэффициент приведения длины для данной схемы крепления:

Задача №2
Проверить устойчивость стержня. Стержень длиной 1 м закреплен так, как показано на рис. 2, сечение – швеллер №16, материал – Ст. 2, запас устойчивости трехкратный. Стержень нагружен сжимающей силой F=98 кН (рис. 2).
 рис. 2
рис. 2
Решение
1. Определяем основные геометрические параметры сечения стержня по ГОСТ 8240-89.
Швеллер №___: А=_____см2, Iу=_____см4, iу=_____см.
2. Определяем категорию стержня в зависимости от гибкости.
Предельная гибкость для материала _________ составляет  =_____.
=_____.
Расчетная гибкость:

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Расчет Fкр ведем по формуле Эйлера:

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
3. Допускаемая нагрузка на стержень:

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
4. Условие устойчивости:

_______________________. Устойчивость стержня ____________.
Практическая работа №17
Устойчивость сжатых стержней. Расчеты на устойчивость
Вариант №12
Задача №1
Рассчитать гибкость стержня (l=1,8м). Круглый стержень диаметром 30мм закреплен так, как показано на рис. 1.
 рис. 1
рис. 1
Решение
Гибкость стержня определяется по формуле:

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Определяем минимальный радиус инерции для круга:

_____________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
Коэффициент приведения длины для данной схемы крепления:

Задача №2
Проверить устойчивость стержня. Стержень длиной 1 м закреплен так, как показано на рис. 2, сечение – швеллер №22, материал – Ст. 3, запас устойчивости трехкратный. Стержень нагружен сжимающей силой F=100 кН (рис. 2).
 рис. 2
рис. 2
Решение
1. Определяем основные геометрические параметры сечения стержня по ГОСТ 8240-89.
Швеллер №___: А=_____см2, Iу=_____см4, iу=_____см.
2. Определяем категорию стержня в зависимости от гибкости.
Предельная гибкость для материала _________ составляет  =_____.
=_____.
Расчетная гибкость:

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Расчет Fкр ведем по формуле Эйлера:

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
3. Допускаемая нагрузка на стержень:

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
4. Условие устойчивости:

_______________________. Устойчивость стержня ____________.
Практическая работа №17
Устойчивость сжатых стержней. Расчеты на устойчивость
Вариант №13
Задача №1
Рассчитать гибкость стержня (l=1м). Круглый стержень диаметром 16мм закреплен так, как показано на рис. 1.
 рис. 1
рис. 1
Решение
Гибкость стержня определяется по формуле:

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Определяем минимальный радиус инерции для круга:

_____________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
Коэффициент приведения длины для данной схемы крепления:

Задача №2
Проверить устойчивость стержня. Стержень длиной 1 м защемлен одним концом, сечение – швеллер №18, материал – Ст. 2, запас устойчивости трехкратный. Стержень нагружен сжимающей силой F=102 кН (рис. 2).
 рис. 2
рис. 2
Решение
1. Определяем основные геометрические параметры сечения стержня по ГОСТ 8240-89.
Швеллер №___: А=_____см2, Iу=_____см4, iу=_____см.
2. Определяем категорию стержня в зависимости от гибкости.
Предельная гибкость для материала _________ составляет  =_____.
=_____.
Расчетная гибкость:

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Расчет Fкр ведем по формуле Эйлера:

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
3. Допускаемая нагрузка на стержень:

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
4. Условие устойчивости:

_______________________. Устойчивость стержня ____________.
Практическая работа №17
Устойчивость сжатых стержней. Расчеты на устойчивость
Вариант №14
Задача №1
Рассчитать гибкость стержня (l=1м). Круглый стержень диаметром 20мм закреплен так, как показано на рис. 1.
 рис. 1
рис. 1
Решение
Гибкость стержня определяется по формуле:

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Определяем минимальный радиус инерции для круга:

_____________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
Коэффициент приведения длины для данной схемы крепления:

Задача №2
Проверить устойчивость стержня. Стержень длиной 1 м закреплен так, как показано на рис. 2, сечение – швеллер №14, материал – Ст. 20, запас устойчивости трехкратный. Стержень нагружен сжимающей силой F=88 кН (рис. 2).
 рис. 2
рис. 2
Решение
1. Определяем основные геометрические параметры сечения стержня по ГОСТ 8240-89.
Швеллер №___: А=_____см2, Iу=_____см4, iу=_____см.
2. Определяем категорию стержня в зависимости от гибкости.
Предельная гибкость для материала _________ составляет  =_____.
=_____.
Расчетная гибкость:

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Расчет Fкр ведем по формуле Эйлера:

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
3. Допускаемая нагрузка на стержень:

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
4. Условие устойчивости:

_______________________. Устойчивость стержня ____________.
Практическая работа №17
Устойчивость сжатых стержней. Расчеты на устойчивость
Вариант №15
Задача №1
Рассчитать гибкость стержня (l=1,5м). Круглый стержень диаметром 18мм закреплен так, как показано на рис. 1.
 рис. 1
рис. 1
Решение
Гибкость стержня определяется по формуле:

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Определяем минимальный радиус инерции для круга:

_____________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
Коэффициент приведения длины для данной схемы крепления:

Задача №2
Проверить устойчивость стержня. Стержень длиной 1 м закреплен так, как показано на рис. 2, сечение – швеллер №20, материал – Ст. 2, запас устойчивости трехкратный. Стержень нагружен сжимающей силой F=100 кН (рис. 2).
 рис. 2
рис. 2
Решение
1. Определяем основные геометрические параметры сечения стержня по ГОСТ 8240-89.
Швеллер №___: А=_____см2, Iу=_____см4, iу=_____см.
2. Определяем категорию стержня в зависимости от гибкости.
Предельная гибкость для материала _________ составляет  =_____.
=_____.
Расчетная гибкость:

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Расчет Fкр ведем по формуле Эйлера:

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
3. Допускаемая нагрузка на стержень:

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
4. Условие устойчивости:

_______________________. Устойчивость стержня ____________.
Практическая работа №17
Устойчивость сжатых стержней. Расчеты на устойчивость
Вариант №16
Задача №1
Рассчитать гибкость стержня (l=1,6м). Круглый стержень диаметром 24мм закреплен так, как показано на рис. 1.
 рис. 1
рис. 1
Решение
Гибкость стержня определяется по формуле:

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Определяем минимальный радиус инерции для круга:

_____________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
Коэффициент приведения длины для данной схемы крепления:

Задача №2
Проверить устойчивость стержня. Стержень длиной 1 м закреплен так, как показано на рис. 2, сечение – швеллер №24, материал – Ст. 3, запас устойчивости трехкратный. Стержень нагружен сжимающей силой F=106 кН (рис. 2).
 рис. 2
рис. 2
Решение
1. Определяем основные геометрические параметры сечения стержня по ГОСТ 8240-89.
Швеллер №___: А=_____см2, Iу=_____см4, iу=_____см.
2. Определяем категорию стержня в зависимости от гибкости.
Предельная гибкость для материала _________ составляет  =_____.
=_____.
Расчетная гибкость:

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Расчет Fкр ведем по формуле Эйлера:

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
3. Допускаемая нагрузка на стержень:

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
4. Условие устойчивости:

_______________________. Устойчивость стержня ____________.
Практическая работа №17
Устойчивость сжатых стержней. Расчеты на устойчивость
Вариант №17
Задача №1
Рассчитать гибкость стержня (l=1,5м). Круглый стержень диаметром 28мм закреплен так, как показано на рис. 1.
 рис. 1
рис. 1
Решение
Гибкость стержня определяется по формуле:

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Определяем минимальный радиус инерции для круга:

_____________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
Коэффициент приведения длины для данной схемы крепления:

Задача №2
Проверить устойчивость стержня. Стержень длиной 1 м защемлен одним концом, сечение – швеллер №27, материал – Ст. 2, запас устойчивости трехкратный. Стержень нагружен сжимающей силой F=110 кН (рис. 2).
 рис. 2
рис. 2
Решение
1. Определяем основные геометрические параметры сечения стержня по ГОСТ 8240-89.
Швеллер №___: А=_____см2, Iу=_____см4, iу=_____см.
2. Определяем категорию стержня в зависимости от гибкости.
Предельная гибкость для материала _________ составляет  =_____.
=_____.
Расчетная гибкость:

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Расчет Fкр ведем по формуле Эйлера:

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
3. Допускаемая нагрузка на стержень:

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
4. Условие устойчивости:

_______________________. Устойчивость стержня ____________.
Практическая работа №17
Устойчивость сжатых стержней. Расчеты на устойчивость
Вариант №18
Задача №1
Рассчитать гибкость стержня (l=1,5м). Круглый стержень диаметром 20мм закреплен так, как показано на рис. 1.
 рис. 1
рис. 1
Решение
Гибкость стержня определяется по формуле:

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Определяем минимальный радиус инерции для круга:

_____________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
Коэффициент приведения длины для данной схемы крепления:

Задача №2
Проверить устойчивость стержня. Стержень длиной 1 м закреплен так, как показано на рис. 2, сечение – швеллер №14, материал – Ст. 20, запас устойчивости трехкратный. Стержень нагружен сжимающей силой F=76 кН (рис. 2).
 рис. 2
рис. 2
Решение
1. Определяем основные геометрические параметры сечения стержня по ГОСТ 8240-89.
Швеллер №___: А=_____см2, Iу=_____см4, iу=_____см.
2. Определяем категорию стержня в зависимости от гибкости.
Предельная гибкость для материала _________ составляет  =_____.
=_____.
Расчетная гибкость:

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Расчет Fкр ведем по формуле Эйлера:

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
3. Допускаемая нагрузка на стержень:

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
4. Условие устойчивости:

_______________________. Устойчивость стержня ____________.
Практическая работа №17
Устойчивость сжатых стержней. Расчеты на устойчивость
Вариант №19
Задача №1
Рассчитать гибкость стержня (l=1м). Круглый стержень диаметром 16мм закреплен так, как показано на рис. 1.
 рис. 1
рис. 1
Решение
Гибкость стержня определяется по формуле:

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Определяем минимальный радиус инерции для круга:

_____________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
Коэффициент приведения длины для данной схемы крепления:

Задача №2
Проверить устойчивость стержня. Стержень длиной 1 м закреплен так, как показано на рис. 2, сечение – швеллер №18, материал – Ст. 3, запас устойчивости трехкратный. Стержень нагружен сжимающей силой F=88 кН (рис. 2).
 рис. 2
рис. 2
Решение
1. Определяем основные геометрические параметры сечения стержня по ГОСТ 8240-89.
Швеллер №___: А=_____см2, Iу=_____см4, iу=_____см.
2. Определяем категорию стержня в зависимости от гибкости.
Предельная гибкость для материала _________ составляет  =_____.
=_____.
Расчетная гибкость:

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Расчет Fкр ведем по формуле Эйлера:

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
3. Допускаемая нагрузка на стержень:

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
4. Условие устойчивости:

_______________________. Устойчивость стержня ____________.
Практическая работа №17
Устойчивость сжатых стержней. Расчеты на устойчивость
Вариант №20
Задача №1
Рассчитать гибкость стержня (l=1,8м). Круглый стержень диаметром 20мм закреплен так, как показано на рис. 1.
 рис. 1
рис. 1
Решение
Гибкость стержня определяется по формуле:

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Определяем минимальный радиус инерции для круга:

_____________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
Коэффициент приведения длины для данной схемы крепления:

Задача №2
Проверить устойчивость стержня. Стержень длиной 1 м закреплен так, как показано на рис. 2, сечение – швеллер №16, материал – Ст. 2, запас устойчивости трехкратный. Стержень нагружен сжимающей силой F=90 кН (рис. 2).
 рис. 2
рис. 2
Решение
1. Определяем основные геометрические параметры сечения стержня по ГОСТ 8240-89.
Швеллер №___: А=_____см2, Iу=_____см4, iу=_____см.
2. Определяем категорию стержня в зависимости от гибкости.
Предельная гибкость для материала _________ составляет  =_____.
=_____.
Расчетная гибкость:

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Расчет Fкр ведем по формуле Эйлера:

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
3. Допускаемая нагрузка на стержень:

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
4. Условие устойчивости:

_______________________. Устойчивость стержня ____________.
Практическая работа №17
Устойчивость сжатых стержней. Расчеты на устойчивость
Вариант №21
Задача №1
Рассчитать гибкость стержня (l=1,5м). Круглый стержень диаметром 30мм закреплен так, как показано на рис. 1.
 рис. 1
рис. 1
Решение
Гибкость стержня определяется по формуле:

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Определяем минимальный радиус инерции для круга:

_____________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
Коэффициент приведения длины для данной схемы крепления:

Задача №2
Проверить устойчивость стержня. Стержень длиной 1 м защемлен одним концом, сечение – швеллер №20, материал – Ст. 20, запас устойчивости трехкратный. Стержень нагружен сжимающей силой F=92 кН (рис. 2).
 рис. 2
рис. 2
Решение
1. Определяем основные геометрические параметры сечения стержня по ГОСТ 8240-89.
Швеллер №___: А=_____см2, Iу=_____см4, iу=_____см.
2. Определяем категорию стержня в зависимости от гибкости.
Предельная гибкость для материала _________ составляет  =_____.
=_____.
Расчетная гибкость:

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Расчет Fкр ведем по формуле Эйлера:

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
3. Допускаемая нагрузка на стержень:

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
4. Условие устойчивости:

_______________________. Устойчивость стержня ____________.
Практическая работа №17
Устойчивость сжатых стержней. Расчеты на устойчивость
Вариант №22
Задача №1
Рассчитать гибкость стержня (l=1м). Круглый стержень диаметром 28мм закреплен так, как показано на рис. 1.
 рис. 1
рис. 1
Решение
Гибкость стержня определяется по формуле:

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Определяем минимальный радиус инерции для круга:

_____________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
Коэффициент приведения длины для данной схемы крепления:

Задача №2
Проверить устойчивость стержня. Стержень длиной 1 м закреплен так, как показано на рис. 2, сечение – швеллер №14, материал – Ст. 3, запас устойчивости трехкратный. Стержень нагружен сжимающей силой F=76 кН (рис. 2).
 рис. 2
рис. 2
Решение
1. Определяем основные геометрические параметры сечения стержня по ГОСТ 8240-89.
Швеллер №___: А=_____см2, Iу=_____см4, iу=_____см.
2. Определяем категорию стержня в зависимости от гибкости.
Предельная гибкость для материала _________ составляет  =_____.
=_____.
Расчетная гибкость:

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Расчет Fкр ведем по формуле Эйлера:

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
3. Допускаемая нагрузка на стержень:

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
4. Условие устойчивости:

_______________________. Устойчивость стержня ____________.
Практическая работа №17
Устойчивость сжатых стержней. Расчеты на устойчивость
Вариант №23
Задача №1
Рассчитать гибкость стержня (l=1,5м). Круглый стержень диаметром 22мм закреплен так, как показано на рис. 1.
 рис. 1
рис. 1
Решение
Гибкость стержня определяется по формуле:

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Определяем минимальный радиус инерции для круга:

_____________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
Коэффициент приведения длины для данной схемы крепления:

Задача №2
Проверить устойчивость стержня. Стержень длиной 1 м закреплен так, как показано на рис. 2, сечение – швеллер №20, материал – Ст. 3, запас устойчивости трехкратный. Стержень нагружен сжимающей силой F=88 кН (рис. 2).
 рис. 2
рис. 2
Решение
1. Определяем основные геометрические параметры сечения стержня по ГОСТ 8240-89.
Швеллер №___: А=_____см2, Iу=_____см4, iу=_____см.
2. Определяем категорию стержня в зависимости от гибкости.
Предельная гибкость для материала _________ составляет  =_____.
=_____.
Расчетная гибкость:

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Расчет Fкр ведем по формуле Эйлера:

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
3. Допускаемая нагрузка на стержень:

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
4. Условие устойчивости:

_______________________. Устойчивость стержня ____________.
Практическая работа №17
Устойчивость сжатых стержней. Расчеты на устойчивость
Вариант №24
Задача №1
Рассчитать гибкость стержня (l=1м). Круглый стержень диаметром 30мм закреплен так, как показано на рис. 1.
 рис. 1
рис. 1
Решение
Гибкость стержня определяется по формуле:

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Определяем минимальный радиус инерции для круга:

_____________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
Коэффициент приведения длины для данной схемы крепления:

Задача №2
Проверить устойчивость стержня. Стержень длиной 1 м закреплен так, как показано на рис. 2, сечение – швеллер №24, материал – Ст. 3, запас устойчивости трехкратный. Стержень нагружен сжимающей силой F=108 кН (рис. 2).
 рис. 2
рис. 2
Решение
1. Определяем основные геометрические параметры сечения стержня по ГОСТ 8240-89.
Швеллер №___: А=_____см2, Iу=_____см4, iу=_____см.
2. Определяем категорию стержня в зависимости от гибкости.
Предельная гибкость для материала _________ составляет  =_____.
=_____.
Расчетная гибкость:

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Расчет Fкр ведем по формуле Эйлера:

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
3. Допускаемая нагрузка на стержень:

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
4. Условие устойчивости:

_______________________. Устойчивость стержня ____________.
Практическая работа №17
Устойчивость сжатых стержней. Расчеты на устойчивость
Вариант №25
Задача №1
Рассчитать гибкость стержня (l=1,5м). Круглый стержень диаметром 20мм закреплен так, как показано на рис. 1.
 рис. 1
рис. 1
Решение
Гибкость стержня определяется по формуле:

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Определяем минимальный радиус инерции для круга:

_____________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________
Коэффициент приведения длины для данной схемы крепления:

Задача №2
Проверить устойчивость стержня. Стержень длиной 1 м защемлен одним концом, сечение – швеллер №16, материал – Ст. 2, запас устойчивости трехкратный. Стержень нагружен сжимающей силой F=92 кН (рис. 2).
 рис. 2
рис. 2
Решение
1. Определяем основные геометрические параметры сечения стержня по ГОСТ 8240-89.
Швеллер №___: А=_____см2, Iу=_____см4, iу=_____см.
2. Определяем категорию стержня в зависимости от гибкости.
Предельная гибкость для материала _________ составляет  =_____.
=_____.
Расчетная гибкость:

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Расчет Fкр ведем по формуле Эйлера:

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________
3. Допускаемая нагрузка на стержень:

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
4. Условие устойчивости:

_______________________. Устойчивость стержня ____________.

















 м
м м
м









