Презентация к уроку "Производная в задачах ЕГЭ", 11 класс

«Возможности приумножаются, если ими пользоваться»

• С её появлением математика перешагнула

из алгебры в математический анализ

• Ньютон назвал её «флюксией» и обозначал

точкой

• Бывает первой, второй,…

• Обозначается штрихом.

Тема урока

И это всё о ней…

(Производная в задачах ЕГЭ)

Цель урока: систематизировать знания и умения по теме «Производная» и рассмотреть применение полученных знаний при решении различного типа задач ЕГЭ.

Задачи урока:

• Образовательные: повторить теоретические сведения по теме по теме «Производная»: формулы и правила дифференцирования, геометрический и физический смысл производной.
• Развивающие: развивать мыслительную деятельность, формировать умения чётко и ясно излагать свои мысли, точно и лаконично формулировать свои ответы.
• Воспитательные: воспитывать умение работать в группе, слушать товарищей, проводить оценку и самооценку.

Производной функции в точке x 0 называется предел

отношения приращения функции к приращению

аргумента при условии, что приращение аргумента стремится к нулю .

Операция нахождение производной функции называется дифференцированием

Производные элементарных функций

Функция

Производная

C

x

kx

kx + b

x r

a x

e x

0

1

k

k

a x lna

e x

Производные элементарных функций

Функция

Производная

log a x

  lnx

sin x

cos x

tg x

ctg x

cosx

- sinx

Правила дифференцирования

1) Постоянный множитель можно вынести за знак производной

(k f(x)) '    = k f '   (x)

2) Производная суммы равна сумме производных

(f(x) + g(x)) '    = f '   (x) + g ' (x)

3) Производная произведения двух функций равна сумме

производной первой функции умноженной на вторую функцию

и первой функции умноженной на производную второй .

(f(x)g(x)) ' = f ' (x)g(x) + f(x)g ' (x)

4) Производная частного двух функций равна дроби, в числителе которой разность производной первой функции умноженной на вторую функцию и первой функции умноженной на производную второй, а в знаменателе квадрат второй функции.

5) Производная сложной функции равна произведению производной внешней функции на производную внутренней функции

(f(g(x))) ' = f ' (g(x))·g ' (x)

f(x) f ' (x)

f ' (x) = 2

f(x) = 2x

f ' (x) = 12x 2 – 2x

f(x) = 4x 3 –x 2

f(x) = e 2x

f ' (x) = 2e 2x

f(x) = 12sin3x

f ' (x) = 36cos3x

f(x) = cos3x

f ' (x) = –3sin3x

f(x) = ln (5-x)

f ' (x) = e x (5x – 1)+5e x

f(x)= e x (5x – 1)

f ' (x) = 78π

f(x) = 78πx

«Мало иметь хороший ум, главное – хорошо его применять» …

Рене Декарт

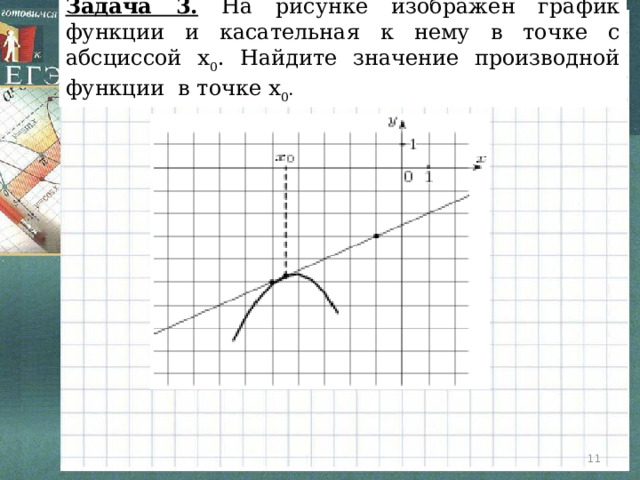
Задача 3. На рисунке изображён график функции и касательная к нему в точке с абсциссой x 0 . Найдите значение производной функции в точке x 0 .

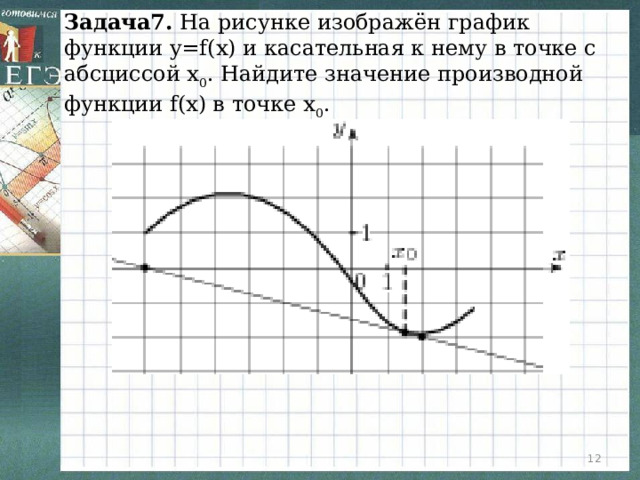
Задача7. На рисунке изображён график функции y=f(x) и касательная к нему в точке с абсциссой x 0 . Найдите значение производной функции f(x) в точке x 0 .

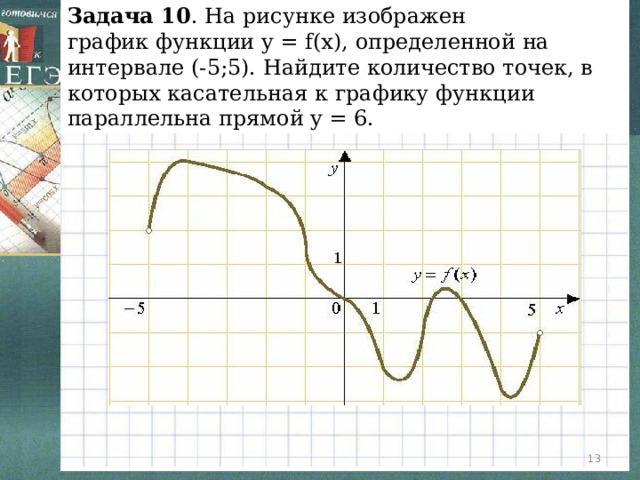
Задача 10 . На рисунке изображен график   функции y = f(x), определенной на интервале (-5;5). Найдите количество точек, в которых касательная к графику функции параллельна прямой y = 6.

Задача 2. Количество вещества, вступившего в химическую реакцию, задается зависимостью (моль). Найдите скорость химической реакции через 3 секунды.

Задача 6. Ма­те­ри­аль­ная точка дви­жет­ся пря­мо­ли­ней­но по за­ко­ну x(t) = 6t 2 – 48t +17 (где x  — рас­сто­я­ние от точки от­сче­та в мет­рах, t  — время в се­кун­дах, из­ме­рен­ное с на­ча­ла дви­же­ния). Най­ди­те ее ско­рость (в м/с) в мо­мент вре­ме­ни t  = 9 с.

Задача12. Ребенок на санках в первые 4 с движения с горки проезжал расстояние, которое задается формулой . Найдите его ускорение в момент времени t = 3 с.

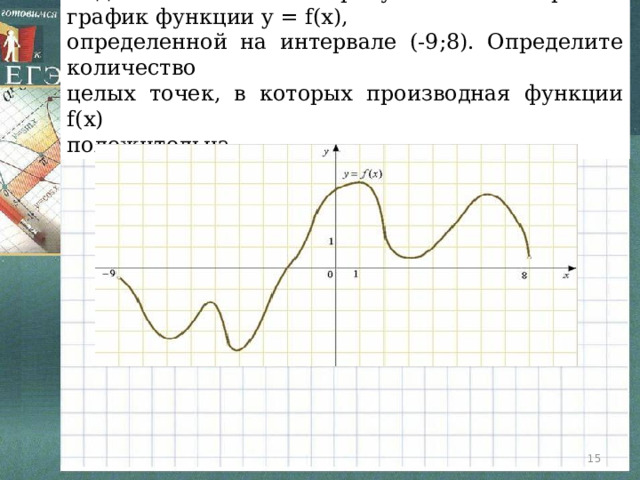
Задача1. На рисунке изображен график   функции y = f(x),

определенной на интервале (-9;8). Определите количество

целых точек, в которых производная функции f(x)

положительна.

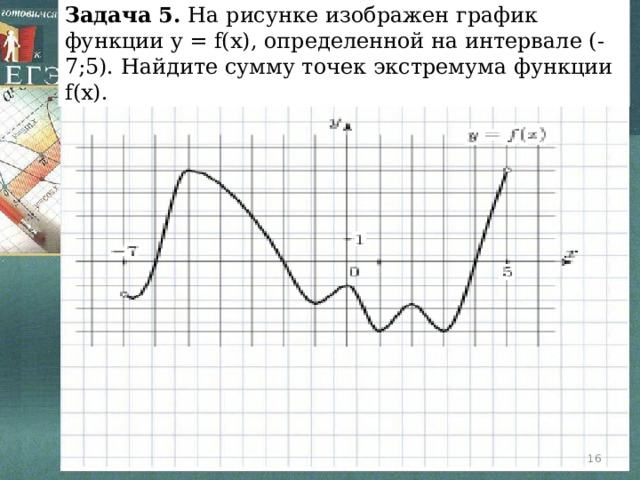
Задача 5. На рисунке изображен график функции y = f(x), определенной на интервале (-7;5). Найдите сумму точек экстремума функции f(x).

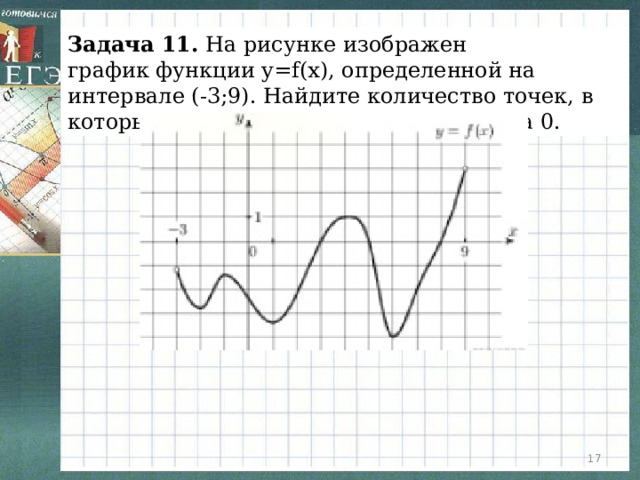
Задача 11. На рисунке изображен график функции y=f(x), определенной на интервале (-3;9). Найдите количество точек, в которых производная функции f(x) равна 0.

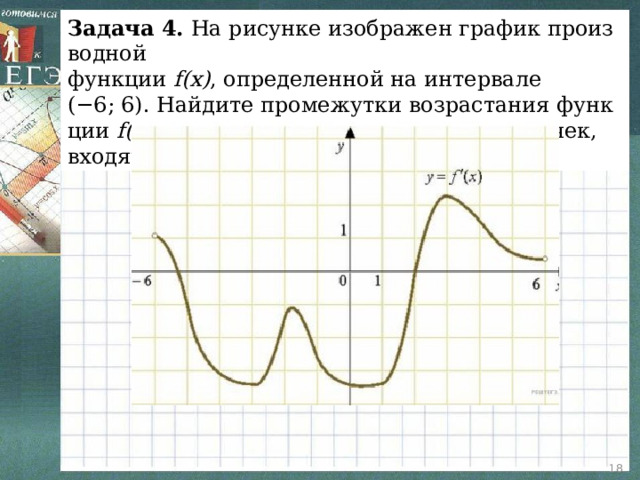
Задача 4. На ри­сун­ке изоб­ра­жен гра­фик про­из­вод­ной

функ­ции f(x) , опре­де­лен­ной на ин­тер­ва­ле (−6; 6). Най­ди­те про­ме­жут­ки воз­рас­та­ния функ­ции f(x) . В от­ве­те ука­жи­те сумму целых точек, вхо­дя­щих в эти про­ме­жут­ки.

Задача 8. На рисунке изображен график производной функции f(x) , определенной на интервале (-9;8). В какой точке отрезка [-8;-4] функция f(x) принимает наименьшее значение.

Задача 9 . На рисунке изображен график производной функции f(x), определенной на интервале (-4;16). Найдите количество точек максимума функции f(x) на отрезке[0;13].

Алгоритм нахождения точек экстремума

• Найти область определения функции.
• Найти производную функции  f  '( x ).
• Найти точки, в которых производная f  '( x ) не существует.
• Найти точки, в которых  f  '( x ) = 0.
• Отметить на числовой прямой область определения функции и все точки, в которых  f  '( x ) = 0 или не существует
• Определить знак  f  '( x ) для каждого промежутка.
• Определить по знакам производной промежутки возрастания и убывания функции и сделать выводы о наличии или отсутствии экстремума и его характере в каждой из критических точек.

Задача 1. Найдите точку максимума функции y = ln(x + 5) – 2x +9

Задача 2. Найти наименьшее значение функции y =(x 2 –4x +4)·e x на отрезке

Работа в парах

1. Найдите точку максимума функции y = ( x + 7)· e 7-x

2. Найдите точку минимума функции y = 4x − ln (x + 11) + 12

3. Найдите точку максимума функции y = x 3 – 108x +11

4. Найдите наименьшее значение функции  на

отрезке

5. Найдите наибольшее значение функции y = x 3 – 192x +11 на

отрезке

• Сегодня я повторил…
• На уроке мне пригодились знания…
• Для меня было сложно…
• На уроке мне понравилось…
• Я смогу на ЕГЭ…

«Сегодня мы учимся вместе: я, ваш учитель, и вы, мои ученики. Но в будущем ученик должен превзойти учителя»

В.А.Сухомлинский