Презентация к занятию по математике по теме Тригонометрические функции числового аргумента

Тема занятия:

«Тригонометрические

функции числового аргумента»

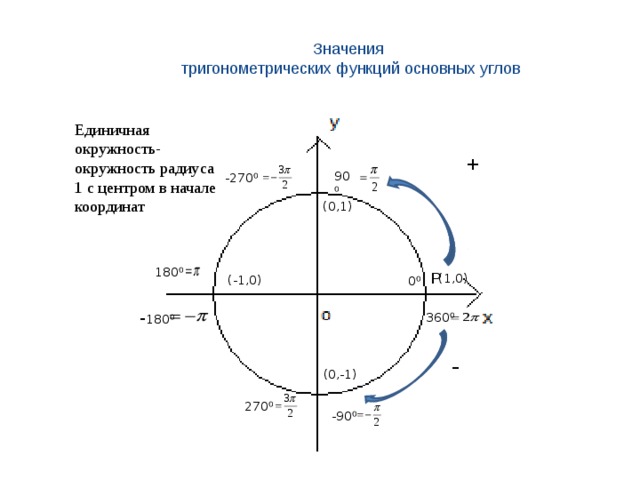
Значения тригонометрических функций основных углов

Единичная окружность-окружность радиуса 1 с центром в начале координат

+

90⁰

-270⁰

(0,1)

180⁰

Р

(1,0)

(-1,0)

0⁰

- 180⁰

360⁰

-

(0,-1)

270⁰

-90⁰

Определение синуса, косинуса, тангенса и котангенса угла поворота

• Синус угла поворота   α  - это ордината точки  A 1 , то есть,  sinα=y .
• Косинусом угла поворота   α  называют абсциссу точки  A 1 , то есть,  cosα=x .
• Тангенс угла поворота   α  - это отношение ординаты точки  A 1  к ее абсциссе, то есть,  tgα=y/x .
• Котангенсом угла поворота   α  называют отношение абсциссы точки  A 1  к ее ординате, то есть,  ctgα=x/y .

Определение синуса, косинуса, тангенса и котангенса числа

Синусом числа   t  называют ординату точки единичной окружности, соответствующей числу  t , то есть,  sint=y .

Косинусом числа   t  называют абсциссу точки единичной окружности, отвечающей числу  t , то есть,  cost=x .

Тангенсом числа   t  называют отношение ординаты к абсциссе точки единичной окружности, соответствующей числу  t , то есть,  tgt=y/x . В другой равносильной формулировке тангенс числа  t  – это отношение синуса этого числа к косинусу, то есть,  tgt=sint/cost .

Котангенсом числа   t  называют отношение абсциссы к ординате точки единичной окружности, соответствующей числу  t , то есть,  ctgt=x/y . Другая формулировка такова: тангенс числа  t  – это отношение косинуса числа  t  к синусу числа  t :  ctgt=cost/sint .

Функция sin  α ,  , называется  синусом.  Функция cos  α ,  , называется  косинусом . Функция tg  α ,  , называется  тангенсом . Функция ctg  α ,  , называется  котангенсом .

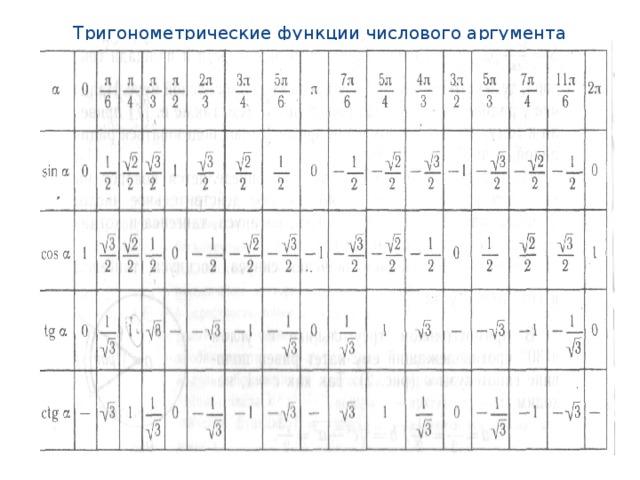
Тригонометрические функции числового аргумента

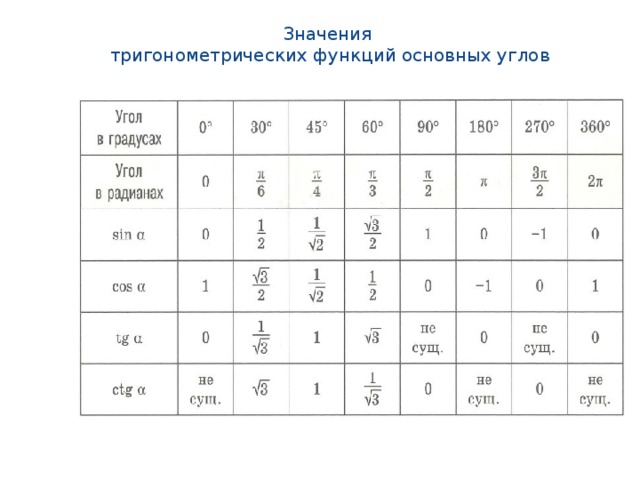
Значения тригонометрических функций основных углов

Знаки тригонометрических функций в четвертях единичной окружности

+

I

II

+

+

-

-

III

IV

-

I

II

III

IV

I

II

+

_

+

_

III

IV

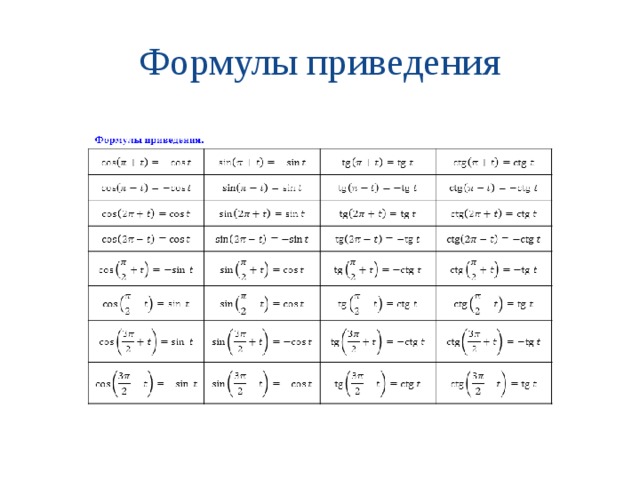
Формулы приведения

Формулы приведения

Название функции не меняется

Название функции меняется на «кофункцию »

Четность и нечетность тригонометрических функций

Формула (1) означает, что косинус – функция четная, а формулы (2), (3), (4) означают, что синус, тангенс и котангенс – функции нечетные, что и требовалось доказать.

Задание

Найдите

Задание

Найдите числовое значение выражения:

Задание

Задание

Самостоятельная работа

Вычислить:

• 1.
• 2.
• 3.
• 4.
• 5.

-

Ответы

1.

2.

3. _

4. _

5. 1