Презентация на тему " Квадратичная функция"

Её свойства и график

Урок алгебры в 8-м классе

Учитель математики: Инсаркин Сергей Борисович

• Функцию вида y = ax 2 + bx + c , где a, b, c - произвольные числа, причём a ≠ 0 , называют квадратичной функцией (« a » называют старшим коэффициентом).
• Примеры:

y = 3x 2 + 5 x + 6 ,

y = 5x 2 – 7x,

y = 1 / 2 x 2 + 1.

• Построить график функции y = x 2 + 8x +7 .
• Выделим полный квадрат, преобразовав функцию к виду: y = a(x + l) 2 + m .

y = x 2 + 2∙4∙x + 4 2 – 4 2 +7 =

= x 2 + 2∙4∙x + 16 – 16 +7

y = (x + 4) 2 – 9

y = x 2 ,  на 4,  на 9

График квадратичной функции – парабола .

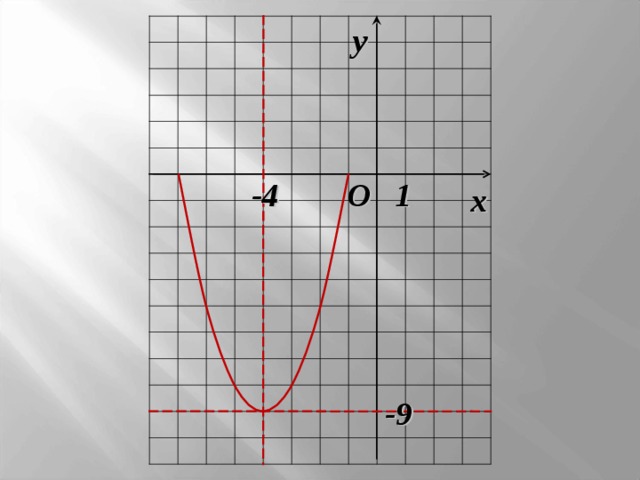
y

O

1

-4

x

-9

• Построить график функции y = x 2 + 3 x + 2 .

y = x 2 + 2∙ 1,5 ∙x + 1,5 2 – 1,5 2 + 2 =

= x 2 + 2∙ 1,5 ∙x + 2,25 – 2,25 + 2

y = (x + 1,5 ) 2 − 0,25

y = x 2 ,  на 1,5,  на 0,25

• Найти координаты вершины параболы А(х в , у в ) по формулам

построить эту точку в координатной плоскости, провести ось симметрии параболы.

• С правой стороны от оси симметрии взять 2-3 значения аргумента (х 1 , х 2 , х 3 ), вычислить значения функции f( х 1 ), f( х 2 ), f( х 3 ) . Отметить точки в координатной плоскости.
• С левой стороны от оси симметрии отметить симметричные точки, построить параболу.

y

y = 2 x 2 + 4 x – 1

А(-1; -3), a  0 – ветви параболы направлены вверх

x

0

1

• Куда направлены ветви параболы?
• Найдите координаты вершины параболы.
• Запишите уравнение прямой, которая является осью симметрии параболы.

• y = - x 2 + 2 x + 1
• y = -3 x 2 – 6 x + 1
• y = 3 x 2 – 12 x
• y = -2x 2 + 8x – 5
• y = x 2 + 4 x + 5

(1; 2), x = 1

(-1; 4), x = -1

(2; -12), x = 2

(2; 3), x = 2

(-2; 1), x = -2

y

Укажите по графику:

наименьшее значение функции;

промежутки убывания и возрастания;

значения аргумента, при которых y  0 ,

y  0 .

А(-2; -4), ветви направлены вверх,

т. к. a  0.

(-  ; - 4 )

( 0 ; +  )

-2

1

0

x

- 1

(- 4 ; 0 )

y

• Определить координаты вершины параболы.
• Уравнение оси симметрии параболы.
• Нули функции.
• Промежутки, в которых функция возрастает, убывает.
• Промежутки, в которых функция принимает положительные значения, отрицательные значения.
• Каков знак коэффициента a ?
• Как зависит положение ветвей параболы от коэффициента a ?

x