Просмотр содержимого документа
«Презентация на тему "Свойства функции (9 класс)"»

Свойства функции

3
Какой из графиков, изображенных на рисунках, задает функцию у=f(х). Почему?
1
у
2
у
х
х
у
у
х
х
4

Продолжите предложение:
- Говорят, что задана функция у=f(х) с областью определения Х, если даны множество Х и правило f…
- Независимая переменная х называется…
- Зависимая переменная у называется…
- Способы задания функции…

Найдите область определения функции.
в)
б)
а)
г)
д)
е)
![Какая из функций, заданных графиками, возрастает (убывает) на промежутке [a;b] ?](https://fsd.multiurok.ru/html/2020/04/20/s_5e9dbd8f407b1/img4.jpg)
Какая из функций, заданных графиками, возрастает (убывает) на промежутке [a;b] ?

Какая из функций ограничена снизу (сверху)?
у
у
3
2
х
х
0
0
у
у
х
х

ИЗУЧАЕМ НОВЫЙ МАТЕРИАЛ
![По графику данной функции найдите наибольшее и наименьшее значения функции. Наибольшее и наименьшее значения функции у у на отрезке . 4 [2;1] . х х 0 2 1](https://fsd.multiurok.ru/html/2020/04/20/s_5e9dbd8f407b1/img7.jpg)
- По графику данной функции найдите наибольшее и наименьшее значения функции.
Наибольшее и наименьшее значения функции
у
у
на
отрезке
.
4
[2;1]
.
х
х
0
2
1

Определение 1. Число m называют наименьшим значением функции у=f(х) на множестве Х, если 1.в Х существует такая точка b, что f(b)=m; 2. для всех х из Х выполняется неравенство f(х) ≥ f(b)
Определение 2.
Число M называют наибольшим значением функции у=f(x) на множестве Х, если
- в Х существует такая точка b, что f(b)=M ;
- Для всех х и Х выполняется неравенство f(x) ≤ f(b)

ВЫПУКЛОСТЬ ФУНКЦИИ
ФУНКЦИЯ ВЫПУКЛА ВНИЗ
ФУНКЦИЯ ВЫПУКЛА ВВЕРХ
У
У
.
.
.
.
Х
Х
0
0

Четные и нечетные функции
- Функцию
у =F(x),х € х
у = F(x), х € х,
Называют четной, если для любого значения х из множества х выполняется равенство
Называют нечетной, если для любого значения х из множества х выполняется равенство
F(-x)=F(x)
F(-x)=-F(x)

- График четной функции симметричен относительно оси у
- График нечетной функции симметричен относительно начала координат
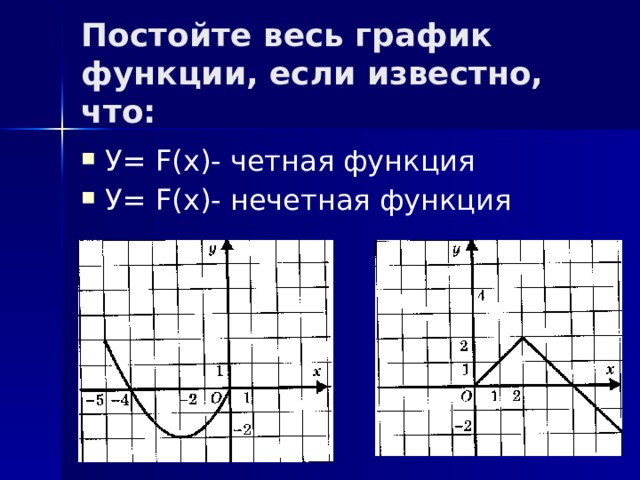
Постойте весь график функции, если известно, что:
- У= F(x)- четная функция
- У= F(x)- нечетная функция
![На каком рисунке изображен график непрерывной функции на отрезке[a, b] 1 2 . . . . . .](https://fsd.multiurok.ru/html/2020/04/20/s_5e9dbd8f407b1/img13.jpg)
На каком рисунке изображен график непрерывной функции на отрезке[a, b]
1
2
.
.
.
.
.
.

Свойства функции
- Область определения
- Монотонность (промежутки возрастания и убывания функции)
- Ограниченность
- Наименьшее и наибольшее значения функции
- Непрерывность функции
- Область значений
- Выпуклость
- Четность и нечетность функции
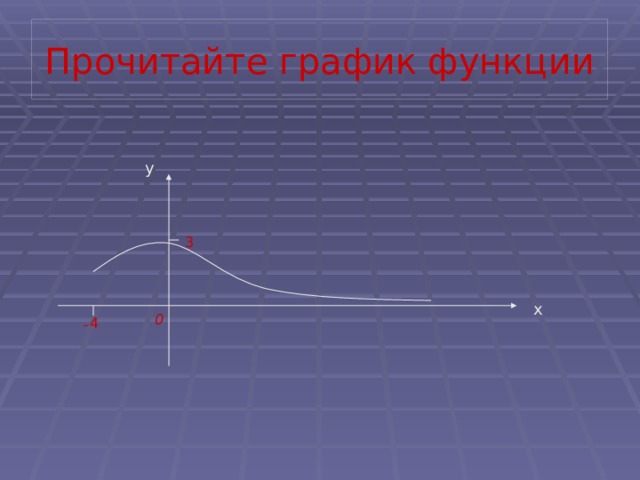
Прочитайте график функции
у
3
х
0
4

Ось отклика
Пословицы в графиках функций
- «Как аукнется, так и откликнется»
- Отклик = ауканью
у
2
1
х
0
1
2
ось ауканья

ИЗОБРАЗИТЕ ГРАФИЧЕСКИ ПОСЛОВИЦЫ
- «Чем дальше в лес, тем больше дров»
- «Выше меры конь не скачет»
- «Ни кола, ни двора»











![Какая из функций, заданных графиками, возрастает (убывает) на промежутке [a;b] ?](https://fsd.multiurok.ru/html/2020/04/20/s_5e9dbd8f407b1/img4.jpg)


![По графику данной функции найдите наибольшее и наименьшее значения функции. Наибольшее и наименьшее значения функции у у на отрезке . 4 [2;1] . х х 0 2 1](https://fsd.multiurok.ru/html/2020/04/20/s_5e9dbd8f407b1/img7.jpg)





![На каком рисунке изображен график непрерывной функции на отрезке[a, b] 1 2 . . . . . .](https://fsd.multiurok.ru/html/2020/04/20/s_5e9dbd8f407b1/img13.jpg)














