Презентация по теме "Строение Солнечной системы. Часть 2

5/21/18

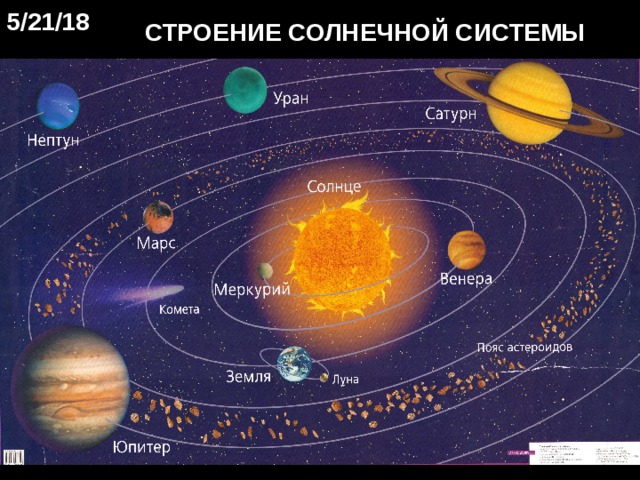
СТРОЕНИЕ СОЛНЕЧНОЙ СИСТЕМЫ

1. Определение расстояний

и размеров тел в Солнечной системе

Определение размеров Земли Эратосфеном

Идея Эратосфена

Измерить длину дуги земного меридиана в линейных единицах и определить какую часть полной окружности эта дуга составляет . Получив эти данные, можно вычислить длину дуги в 1 0 , а затем длину окружности и величину её радиуса, т. е. радиус земного шара. Очевидно, что длина дуги меридиана в градусной мере равна разности географических широт двух пунктов: φ В – φ А .

Эратосфен (276 г. до н.э. – 194 г. до н.э.

Базис

Определение расстояния до недоступного предмета

Угол АСВ , под которым из недоступного места виден базис, называется параллаксом .

С

В

А

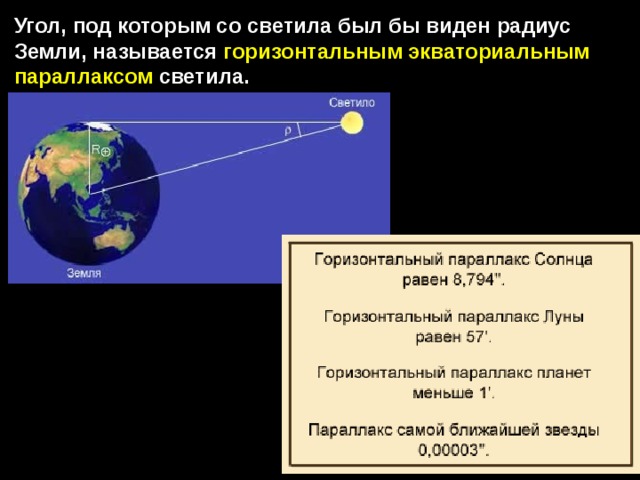
Угол, под которым со светила был бы виден радиус Земли, называется горизонтальным экваториальным параллаксом светила.

Определение расстояния до светила

о

D

о

Углы p о малы, поэтому их синусы можно заменить самими углами,

т.е. sin p о ≈ p о если величина угла выражена в радианах.

Если p о выражен в секундах дуги, то sin p о ≈ p о / 206 265 ” ,

т.к. 1 радиан = 57,3 o = 3 438 ’ = 206 265 ”.

Поэтому расстояние до светила определяют по формуле

Задача. Зная горизонтальный параллакс Луны и экваториальный радиус Земли (6378 км), найти расстояние от Земли до Луны.

D

Дано: Решение:

p  = 57’02’’ D  = 206 265‘‘ * R ⊕ / p 

R ⊕ = 6378 км D  = 206 265‘‘ * 6378 км / 3422‘‘

Найти: D  D  ≈ 384 400 км

Ответ: 384 400 км

Радиолокационный метод определения расстояний до планет.

Посылают кратковременный импульс, который затем принимают после отражения.

Скорость распространения радиоволн равна скорости света в вакууме:

с = 299 792 458 м/с .

Из радиолокационных наблюдений Венеры получено следующее значение астрономической единицы:

1 а.е. = 149 597 868 ± 0,7 км

Вычисление линейных размеров тел Солнечной системы

R

R

о

D



 - угловой радиус небесного тела

о

где, D – расстояние до светила

R = D sin 

R ⊕ = D sin p

R ⊕ - радиус Земли

R = R ⊕ sin  / sin p

ρ – угловой радиус светила

R = R ⊕  / p

p – горизонтальный параллакс

Задача. Во сколько раз линейный радиус Солнца превышает радиус Земли, если угловой радиус Солнца 16’?

Дано: Решение:

 = 16’ R  = R ⊕   / p

p = 8,8” R  = (16*60”/8,8”) R ⊕ ≈ 109 R ⊕

Найти: R 

Ответ: ≈ 109 R ⊕

2. Обобщение и уточнение Ньютоном законов Кеплера

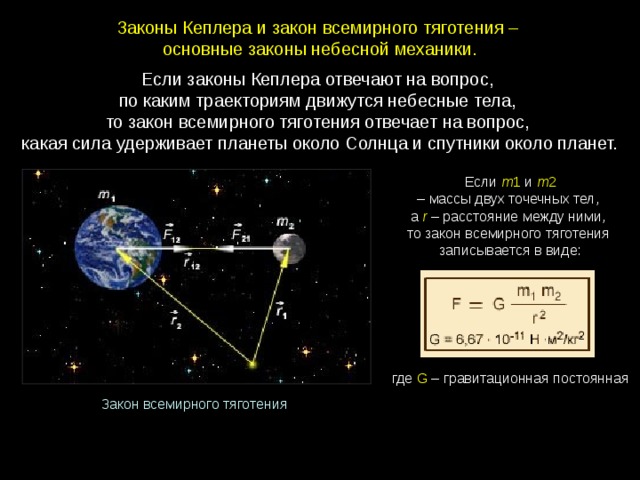
Законы Кеплера и закон всемирного тяготения –

основные законы небесной механики.

Если законы Кеплера отвечают на вопрос,

по каким траекториям движутся небесные тела,

то закон всемирного тяготения отвечает на вопрос,

какая сила удерживает планеты около Солнца и спутники около планет.

Если  m 1 и  m 2 – массы двух точечных тел,

а  r – расстояние между ними,

то закон всемирного тяготения 

записывается в виде:

где G – гравитационная постоянная

Закон всемирного тяготения

Уильям Гершель   (1738–1822) в 1781 году с помощью телескопа открыл планету  Уран , не видимую невооруженным глазом  

Так выглядит Уран

при наблюдении

в наземный телескоп

После открытия Урана астрономы обратили внимание на то, что его орбита

  не соответствовала закону всемирного тяготения Ньютона, претерпевая постоянные отклонения.

Это и навело на мысль о существовании еще одной планеты за Ураном,

которая могла бы своим гравитационным притяжением 

искажать траекторию движения седьмой планеты.

Нептун в наземный телескоп

Английский математик  Джон Адамс  и французский астроном  Урбен Леверье

в 1845 году независимо друг от друга сделали расчет примерного места расположения планеты, возмущающей движение Урана.

Сделав расчет Леверье , убедил астронома Берлинской обсерватории 

Иоганна Галле начать поиск новой планеты.

Расчеты были настолько точны, что неизвестная планета, названная Нептуном , была обнаружена в первую же ночь наблюдений 23 сентября 1846 года.

История открытия Нептуна полностью подтвердила 

закон всемирного тяготения Ньютона.

Это был триумф небесной механики, торжество гелиоцентрической системы.

Урбен Леверье

Поиски девятой планеты Солнечной системы в 1915 году организовал американский астроном  Персиваль Ловелл   , но только в 1930 году Плутон  открыл сотрудник обсерватории Ловелла  Клайд Томбо .

В августе 2006 года на ассамблее Международного астрономического союза решено лишить Плутон статуса планеты Солнечной системы. Теперь он имеет право называться лишь "карликовой планетой".

Около 2,5 тыс. астрономов, собравшихся на ассамблею, определили такие критерии планеты:

• объект должен находиться на орбите вокруг звезды, но сам не должен быть звездой;
• он должен обладать достаточной массой для того, чтобы его собственная гравитация позволяла ему сохранять более или менее сферическую форму;
• на его орбите не должно быть других небесных тел.

Открытый в 1930 году Плутон лишен планетного статуса, поскольку не соответствует третьему из этих параметров - его орбита пересекается с планетой Нептуна .

Таким образом теперь в Солнечной системе осталось только восемь планет: Юпитер, Сатурн, Уран, Нептун, Земля, Венера, Марс и Меркурий.

Клайд Томбо

Иоганн Кеплер открыл свои законы эмпирическим путем. Исаак Ньютон вывел законы Кеплера из закона всемирного тяготения. В 1679 году Исаак Ньютон показал, что  любое тело в поле тяготения шарообразного тела могут двигаться  по окружности, эллипсу, параболе и гиперболе . В этом заключается первый обобщенный Ньютоном закон Кеплера.

Конические сечения и космические орбиты

  Формулировка второго закона Кеплера не потребовала обобщения.

Для определения масс небесных тел важное значение имеет обобщение

Ньютоном третьего закона Кеплера на любые системы обращающихся тел.

В обобщенном виде  третий  закон Кеплера обычно формулируется так:

квадраты периодов обращения двух тел вокруг Солнца (T 1 2 и T 2 2 ) ,

помноженные на сумму масс каждого тела и Солнца (M 1 + М  и M 2 + М  ) ,

относятся как кубы больших полуосей их орбит (a 1 3 и  a 2 3 ) .

  Обобщенный третий закон Кеплера справедлив для любых двух независимых систем, каждая из которых состоит из центрального тела и спутников, взаимодействующих по закону всемирного тяготения.

  Масса планеты обычно велика по сравнению с массой спутника, поэтому с достаточной степенью точности можно вычислить отношения масс двух планет по формуле:

Задача. Вычислить массу Юпитера, зная, что один из его спутников (Ио) совершает

оборот вокруг планеты за 1,77 сут на расстоянии 422 тыс.км от Юпитера.   

Дано: Решение:

М 2 =1

Т 2 =27,32 д

а 2 =3,84*10 5 км М 1 = (Т 2 /Т 1 ) 2 (а 1 /а 2 ) 3 М 2

Т 1 =1,77 д М 1 = (27,32/1,77) 2 * (422000/384000) 3 * М 2

а 1 =4,22*10 5 км М 1 ≈ 316 М 2

Найти: М 1

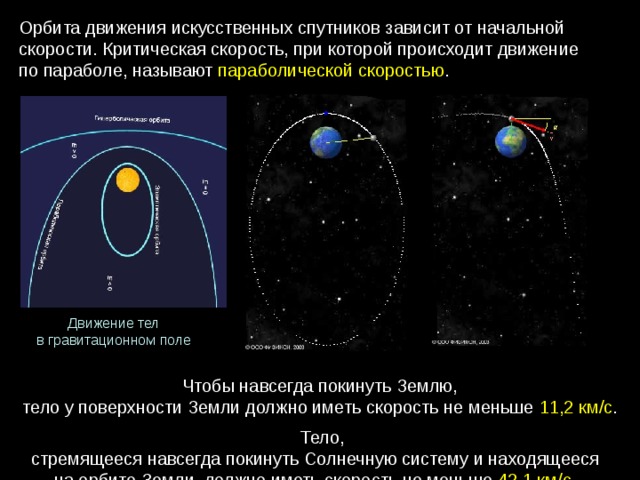
Орбита движения искусственных спутников зависит от начальной скорости. Критическая скорость, при которой происходит движение по параболе, называют параболической скоростью .

Движение тел 

в гравитационном поле 

Чтобы навсегда покинуть Землю, тело у поверхности Земли должно иметь скорость не меньше  11,2 км/с .

Тело, стремящееся навсегда покинуть Солнечную систему и находящееся 

на орбите Земли, должно иметь скорость не меньше  42,1 км/с .

Подготовить сообщения (доклады):

• Первый искусственный спутник Земли.

• Взгляды древних на строение мира

• Геоцентрическая система.

• Гелиоцентрическая система.

• Открытие планет Солнечной системы.

• Определение расстояний до тел Солнечной системы.

• Определение размеров тел Солнечной системы.

• Радиолокация тел Солнечной системы.