Рабочая программа учебного предмета «Геометрия» для 8 класса составлена в соответствии с ФГОС ООО (приказ Министерства образования и науки РФ от 17.12.2010 г. № 1897, с изменениями приказ от 31.12.2015 г. № 1577), с основной образовательной программой основного общего образования СОШ. Содержание реализуется с помощью учебника «Геометрия» для 7-9 класса , авторы: Л.С.Атанасян и др. М.: -2017
Планируемые результаты освоения учебного предмета
Программа обеспечивает достижение следующих результатов освоения образовательной программы основного общего образования:
личностные:
сформированность ответственного отношения к учению, готовность и способности обучающихся к саморазвитию и самообразованию на основе мотивации к обучению и познанию, выбору дальнейшего образования на базе ориентировки в мире профессий и профессиональных предпочтений, осознанному построению индивидуальной образовательной траектории с учётом устойчивых познавательных интересов;
сформированность целостного мировоззрения, соответствующего современному уровню развития науки и общественной практики;
сформированность коммуникативной компетентности в общении и сотрудничестве со сверстниками, старшими и младшими, в образовательной, общественно полезной, учебно-исследовательской, творческой и других видах деятельности;
умение ясно, точно, грамотно излагать свои мысли в устной и письменной речи, понимать смысл поставленной задачи, выстраивать аргументацию, приводить примеры и контрпримеры;
представление о математической науке как сфере человеческой деятельности, об этапах её развития, о её значимости для развития цивилизации;
критичность мышления, умение распознавать логически некорректные высказывания, отличать гипотезу от факта;
креативность мышления, инициатива, находчивость, активность при решении алгебраических задач;
умение контролировать процесс и результат учебной математической деятельности;
способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений.
метапредметные:
умение самостоятельно планировать альтернативные пути достижения целей, осознанно выбирать наиболее эффективные способы решения учебных и познавательных задач;
умение осуществлять контроль по результату и по способу действия на уровне произвольного внимания и вносить необходимые коррективы;
умение адекватно оценивать правильность или ошибочность выполнения учебной задачи, её объективную трудность и собственные возможности её решения;
осознанное владение логическими действиями определения понятий, обобщения, установления аналогий, классификации на основе самостоятельного выбора оснований и критериев, установления родовидовых связей;
умение устанавливать причинно-следственные связи; строить логическое рассуждение, умозаключение (индуктивное, дедуктивное и по аналогии) и выводы;
умение создавать, применять и преобразовывать знаково- символические средства, модели и схемы для решения учебных и познавательных задач;
умение организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками: определять цели, распределение функций и ролей участников, взаимодействие и общие способы работы; умение работать в группе: находить общее решение и разрешать конфликты на основе согласования позиций и учёта интересов; слушать партнёра; формулировать, аргументировать и отстаивать своё мнение;
сформированность учебной и общепользовательской компетентности в области использования информационно-коммуникационных технологий (ИКТ-компетентности);
9) первоначальные представления об идеях и о методах математики как об универсальном языке науки и техники, о средстве моделирования явлений и процессов;
умение видеть математическую задачу в контексте проблемной ситуации в других дисциплинах, в окружающей жизни;
умение находить в различных источниках информацию, необходимую для решения математических проблем, и представлять её в понятной форме; принимать решение в условиях неполной и избыточной, точной и вероятностной информации;
умение понимать и использовать математические средства наглядности (рисунки, чертежи, схемы и др.) для иллюстрации, интерпретации, аргументации;
умение выдвигать гипотезы при решении учебных задач и понимать необходимость их проверки;
умение применять индуктивные и дедуктивные способы рассуждений, видеть различные стратегии решения задач;
понимание сущности алгоритмических предписаний и умение действовать в соответствии с предложенным алгоритмом;
умение самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических проблем;
умение планировать и осуществлять деятельность, направленную на решение задач исследовательского характера.
предметные:
Предметным результатом изучения курса является сформированность следующих умений:
• пользоваться геометрическим языком для описания предметов окружающего мира;
• распознавать геометрические фигуры, различать их взаимное расположение;
• изображать геометрические фигуры; выполнять чертежи по условию задачи; осуществлять преобразования фигур;
• распознавать на чертежах, моделях и в окружающей обстановке основные пространственные тела, изображать их;
• в простейших случаях строить сечения и развертки пространственных тел;
• проводить операции над векторами, вычислять длину и координаты вектора, угол между векторами;
• вычислять значения геометрических величин(длин, углов, площадей, объемов); в том числе: для углов от 0 до 180° определять значения тригонометрических функций по заданным значениям углов; находить значения тригонометрических функций по значению одной из них, находить стороны, углы и вычислять площади треугольников, длины ломаных, дуг окружности, площадей основных геометрических фигур и фигур, составленных из них;
• решать геометрические задачи, опираясь на изученные свойства фигур и отношений
между ними, применяя дополнительные построения, алгебраический и тригонометрический аппарат, правила симметрии;
• проводить доказательные рассуждения при решении задач, используя известные теоремы, обнаруживая возможности для их использования;
• решать простейшие планиметрические задачи в пространстве.
Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
• описания реальных ситуаций на языке геометрии;
• расчетов, включающих простейшие тригонометрические формулы;
• решения геометрических задач с использованием тригонометрии;
• решения практических задач, связанных с нахождением геометрических величин (используя при необходимости справочники и технические средства);
• построений с помощью геометрических инструментов (линейка, угольник, циркуль,
транспортир).
В результате изучения геометрии обучающийся научится:
Наглядная геометрия
1) распознавать на чертежах, рисунках, моделях и в окружающем мире плоские и пространственные геометрические фигуры;
2) распознавать развёртки куба, прямоугольного параллелепипеда;
3) определять по линейным размерам развёртки фигуры линейные размеры самой фигуры и наоборот;
4) вычислять объём прямоугольного параллелепипеда.
Обучающийся получит возможность:
5) вычислять объёмы пространственных геометрических фигур, составленных из прямоугольных параллелепипедов;
6) углубить и развить представления о пространственных геометрических фигурах;
7) применять понятие развёртки для выполнения практических расчётов.
Геометрические фигуры
Обучающийся научится:
1) пользоваться языком геометрии для описания предметов окружающего мира и их взаимного расположения;
2) распознавать и изображать на чертежах и рисунках геометрические фигуры и их конфигурации;
3) находить значения длин линейных элементов фигур и их отношения, градусную меру углов от 0 до 180°, применяя определения, свойства и признаки фигур и их элементов, отношения фигур (равенство, подобие, симметрии, поворот, параллельный перенос);
4) оперировать с начальными понятиями тригонометрии
и выполнять элементарные операции над функциями углов;
5) решать задачи на доказательство, опираясь на изученные свойства фигур и отношений между ними и применяя изученные методы доказательств;
6) решать несложные задачи на построение, применяя основные алгоритмы построения с помощью циркуля и линейки;
7) решать простейшие планиметрические задачи в пространстве.
Обучающийся получит возможность:
8) овладеть методами решения задач на вычисления и доказательства: методом от противного, методом подобия, методом перебора вариантов и методом геометрических мест точек;
9) приобрести опыт применения алгебраического и тригонометрического аппарата и идей движения при решении геометрических задач;
10) овладеть традиционной схемой решения задач на построение с помощью циркуля и линейки: анализ, построение, доказательство и исследование;
11) научиться решать задачи на построение методом геометрического места точек и методом подобия;
12) приобрести опыт исследования свойств планиметрических фигур с помощью компьютерных программ.
Измерение геометрических величин
Обучающийся научится:
1) использовать свойства измерения длин, площадей и углов при решении задач на нахождение длины отрезка, длины окружности, длины дуги окружности, градусной меры угла;
2) вычислять длины линейных элементов фигур и их углы, используя формулы длины окружности и длины дуги окружности, формулы площадей фигур;
3) вычислять площади треугольников, прямоугольников, параллелограммов, трапеций, кругов и секторов;
4) вычислять длину окружности, длину дуги окружности;
5) решать задачи на доказательство с использованием формул длины окружности и длины дуги окружности, формул площадей фигур;
6) решать практические задачи, связанные с нахождением геометрических величин (используя при необходимости справочники и технические средства).
Обучающийся получит возможность:
7) вычислять площади фигур, составленных из двух или более прямоугольников, параллелограммов, треугольников, круга и сектора;
8) вычислять площади многоугольников, используя отношения равновеликости и равносоставленности;
9) приобрести опыт применения алгебраического и тригонометрического аппарата и идей движения при решении задач на вычисление площадей многоугольников.
| № § | Содержание материала | Авторская программа (Бурмистрова Т.А. «Геометрия 7-9 классы. Сборник рабочих программ». Москва; «Просвещение», для учебников авторов Л.С.Атанасян, В.Ф.Бутузов, С.Б.Кадомцев и др. «Геометрия. 7-9 классы») | Рабочая программа |
|
| Глава V. Четырехугольники | 14 | 14 |
|
| Глава VI. Площадь | 14 | 14 |
|
| Глава VII. Подобные треугольники | 19 | 19 |
|
| Глава VIII. Окружность | 17 | 17 |
|
| Повторение. Решение задач
| 4
| 6
|
| ИТОГО | 68 | 70 |
Календарно-тематическое планирование
| № урока | Наименования разделов и тем | Плановые сроки прохождения | Скорректи-рованные сроки прохождения |
|
| Повторение |
|
|
|
| 1 | Урок вводного повторения | 02.09-06.09 |
|
|
| 2 | Урок вводного повторения | 02.09-06.09 |
|
|
|
| Четырехугольники |
|
|
|
| 3 | Многоугольник. Выпуклый многоугольник | 09.09-13.09 |
|
|
| 4 | Четырехугольник | 09.09-13.09 |
|
|
| 5 | Параллелограмм | 16.09-20.09 |
|
|
| 6 | Свойства и признаки параллелограмма | 16.09-20.09 |
|
|
| 7 | Решение задач на свойства и признаки параллелограмма. | 23.09-27.09 |
|
|
| 8 | Трапеция | 23.09-27.09 |
|
|
| 9 | Теорема Фалеса. | 30.09-04.10 |
|
|
| 10 | Задачи на построение циркулем и линейкой. | 30.09-04.10 |
|
|
| 11 | Прямоугольник | 07.10-11.10 |
|
|
| 12 | Ромб и квадрат | 07.10-11.10 |
|
|
| 13 | Осевая и центральная симметрии | 14.10-18.10 |
|
|
| 14 | Решение задач. | 14.10-18.10 |
|
|
| 15 | Решение задач. | 21.10-25.10 |
|
|
| 16 | КОНТРОЛЬНАЯ РАБОТА №1 «Четырехугольники» | 21.10-25.10 |
|
|
|
| Площадь |
|
|
|
| 17 | Анализ контрольной работы. Понятие площади многоугольника. Площадь квадрата | 05.11-08.11 |
|
|
| 18 | Площадь прямоугольника | 05.11-08.11 |
|
|
| 19 | Площадь параллелограмма | 11.11-15.11 |
|
|
| 20 | Площадь треугольника | 11.11-15.11 |
|
|
| 21 | Площадь трапеции | 18.11-22.11 |
|
|
| 22 | Решение задач по теме «Площадь треугольника» | 18.11-22.11 |
|
|
| 23 | Решение задач «Площадь многоугольника» | 25.11-29.11 |
|
|
| 24 | Тестирование по теме «Решение задач на нахождение площади» | 25.11-29.11 |
|
|
| 25 | Теорема Пифагора | 02.12-06.12 |
|
|
| 26 | Теорема, обратная теореме Пифагора | 02.12-06.12 |
|
|
| 27 | Решение задач на применение теоремы Пифагора и обратной ей теоремы. | 09.12-13.12 |
|
|
| 28 | Решение задач. | 09.12-13.12 |
|
|
| 29 | Решение задач. | 16.12-20.12 |
|
|
| 30 | КОНТРОЛЬНАЯ РАБОТА №2 «Площадь» | 16.12-20.12 |
|
|
|
| Подобные треугольники |
|
|
|
| 31 | Анализ контрольной работы. Понятие площади многоугольника. Площадь квадрата | 23.12-27.12 |
|
|
| 32 | Площадь прямоугольника | 23.12-27.12 |
|
|
| 33 | Площадь параллелограмма | 09.01-11.01 |
|
|
| 34 | Площадь треугольника | 09.01-11.01 |
|
|
| 35 | Площадь трапеции | 13.01-17.01 |
|
|
| 36 | Решение задач по теме «Площадь треугольника» | 13.01-17.01 |
|
|
| 37 | Решение задач «Площадь многоугольника» | 20.01-24.01 |
|
|
| 38 | Тестирование по теме «Решение задач на нахождение площади» | 20.01-24.01 |
|
|
| 39 | Теорема Пифагора | 27.01-31.01 |
|
|
| 40 | Теорема, обратная теореме Пифагора | 27.01-31.01 |
|
|
| 41 | Решение задач на применение теоремы Пифагора и обратной ей теоремы. | 03.02-07.02 |
|
|
| 42 | Решение задач. | 03.02-07.02 |
|
|
| 43 | Решение задач. | 10.02-14.02 |
|
|
| 44 | КОНТРОЛЬНАЯ РАБОТА №2 «Площадь» | 10.02-14.02 |
|
|
| 45 | Анализ контрольной работы. Взаимное расположение прямой и окружности | 17.02-21.02 |
|
|
|
| Окружность |
|
|
|
| 46 | Касательная к окружности | 17.02-21.02 |
|
|
| 47 | Касательная к окружности,. Решение задач | 24.02-28.02 |
|
|
| 48 | Градусная мера дуги окружности | 24.02-28.02 |
|
|
| 49 | Теорема о вписанном угле | 02.03-06.03 |
|
|
| 50 | Теорема об отрезках пересекающихся хорд | 02.03-06.03 |
|
|
| 51 | Решение задач по теме «Центральные и вписанные углы». | 09.03-13.03 |
|
|
| 52 | Свойства биссектрисы угла | 09.03-13.03 |
|
|
| 53 | Серединный перпендикуляр. | 16.03-20.03 |
|
|
| 54 | Теорема о точке пересечении высот треугольника | 16.03-20.03 |
|
|
| 55 | Вписанная окружность | 30.03-03.04 |
|
|
| 56 | Свойство описанного четырёхугольника | 30.03-03.04 |
|
|
| 57 | Описанная окружность | 06.04-10.04 |
|
|
| 58 | Свойство вписанного четырёхугольника | 06.04-10.04 |
|
|
| 59 | Решение задач | 13.04-17.04 |
|
|
| 60 | Тестирование по теме «Окружность» | 13.04-17.04 |
|
|
| 61 | КОНТРОЛЬНАЯ РАБОТА №5 «Окружность» | 20.04-24.04 |
|
|
|
| Итоговое повторение |
|
|
|
| 62 | Четырехугольники. | 20.04-24.04 |
|
|
| 63 | Площадь четырехугольника. | 27.04-01.05 |
|
|
| 64 | Подобные треугольники. | 27.04-01.05 |
|
|
| 65 | Окружность. | 04.05-08.05 |
|
|
| 66 | Касательная к окружности | 04.05-08.05 |
|
|
| 67 | Итоговое контрольная работа | 11.05-15.05 |
|
|
| 68 | Решение задач | 11.05-15.05 |
|
|
| 69 | Решение задач | 18.05-22.05 |
|
|
| 70 | Итоговый урок | 18.05-22.05 |
|
|
Входная контрольная работа по геометрии 8 класс
Часть 1.
При выполнении заданий с выбором ответа обведите номер выбранного ответа в работе. Если Вы обвели не тот номер, то зачеркните обведённый номер крестиком и затем обведите номер нового ответа.
A1. Через точку, не лежащую на прямой, можно провести …
две прямые, параллельные данной прямой
только одну прямую, параллельную данной
ни одной прямой, параллельной данной
множество параллельных прямых
A2. Один из смежных углов на 20° больше другого. Найдите больший угол.
700
800
900
1000
A3. Точка М делит отрезок АВ на две части, одна из которой в 3 раза больше другой. Найдите длину большей части, если длина отрезка АВ равна 60 см.
45 см
30 см
15 см
другой ответ
A4. По данным рисунка ответьте на следующий вопрос: в какой из указанных пар углы являются соответственными?
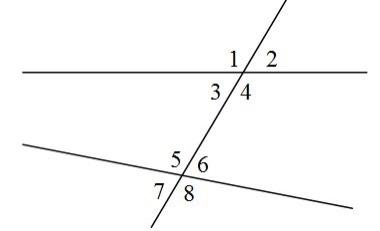
1 и 4
1 и 5
4 и 6
4 и 5
A5. Через две любые точки А и В можно провести:
только две прямые
только одну прямую
ни одной прямой
множество прямых
А6. Найдите сумму углов 1 + 2 + 3, изображенных на рисунке.
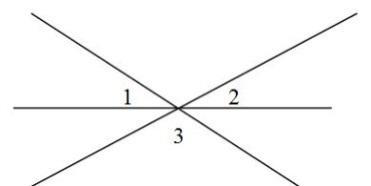
900
1500
1800
3600
А7. С какими из предложенных измерений сторон может существовать треугольник?
10 см, 6 см, 8 см
70 см, 30 см, 30 см
60 см, 30 см, 20 см
30 см, 30 см, 80 см
А8. Выберите верное утверждение из предложенных:
Градусная мера прямого угла равна 900
Градусная мера острого угла больше 900
При параллельных прямых и секущей накрест лежащие углы в сумме образуют 1800
Два треугольника равны, если соответствующие углы равны
А9. На луче с началом в точке А отмечены точки В и С. АВ = 19,2 см, АС=12,4 см. Чему равен отрезок ВС?
6,8 см
5,8 см
31,6 см
Недостаточно условий
А10. Хорда АВ равна 38 см. ОА и ОВ – радиусы окружности, причем угол АОВ равен 900. Найдите расстояние от точки О до хорды АВ.
30,5 см
26 см
19 см
12 см
А11. В прямоугольном треугольнике гипотенуза равна 10 см, а один из катетов – 5 см. Найдите наибольший из острых углов данного треугольника.
900
300
600
450
А12. Прямые а и b параллельны, с-секущая. Разность двух углов, образованных этими прямыми, равна 1500. Чему равно отношение большего из этих углов к меньшему?
14
10
11
9
А13. Выберите верное утверждение.
Через любую точку можно провести только одну прямую
Сумма смежных углов равна 1800
Если при пересечении двух прямых третьей прямой соответственные углы составляют в сумме 1800, то эти две прямые параллельны
Через любые две точки проходит более одной прямой
А14. Выберите верное утверждение.
Если две параллельные прямые пересечены третьей прямой, то внутренние односторонние углы равны
Смежные углы равны
Две прямые, перпендикулярные к третьей, не пересекаются
Если угол равен 300, то смежный с ним равен 600
А15. Выберите верное утверждение.
Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны
Каждая сторона треугольника меньше разности двух других сторон
Если две стороны и угол одного треугольника соответственно равны двум сторонам и углу другого треугольника, то такие треугольники равны
Если три угла одного треугольника соответственно равны трем углам другого треугольника, то такие треугольники равны
Часть 2.
Полученный ответ на задание записывается в отведённом для этого месте. Каждое задание предполагает краткий ответ. В задаче в ответ запишите только число или числа (наименования указывать не надо). Если ответ содержит несколько чисел, разделяйте их точкой с запятой (;) и записывайте числа в порядке возрастания. Если ответом является обыкновенная дробь, то переведите ее в десятичную дробь и запишите в ответ десятичную дробь.
В случае записи неверного ответа зачеркните его и запишите рядом новый.
B1. Дан отрезок АВ=46 см. Точка М – середина отрезка АВ, точка К – середина отрезка МВ. Найти длину отрезка АК.
Ответ:____________________________________
B2. Один из смежных углов в семь раз меньше другого. Найдите эти углы.
Ответ:____________________________________
B3. Сумма гипотенузы СЕ и катета CD прямоугольного треугольника СDE равна 31, а их разность равна 3 см. Найдите расстояние от вершины С до прямой DE.
Ответ:____________________________________
В4. Два острых угла прямоугольного треугольника относятся как 4 : 5. Найдите больший острый угол. Ответ дайте в градусах.
Ответ:____________________________________
В5. В равнобедренном треугольнике АВС с основанием АС внешний угол при вершине С равен 1430. Найдите величину угла АВС. Ответ дайте в градусах.
Ответ:___________________________________
Контрольная работа №1
Четырехугольники
Вариант 1
А1. Периметр параллелограмма ABCD равен 80 см.  А = 30о, а перпендикуляр ВН к прямой АD равен 7,5 см. Найдите стороны параллелограмма
А = 30о, а перпендикуляр ВН к прямой АD равен 7,5 см. Найдите стороны параллелограмма
А2. Докажите, что у равнобедренной трапеции углы при основании равны.
А3. Постройте ромб по двум диагоналям. Сколько осей симметрии у ромба?
В1. Точки Р, К, L, M – середины сторон ромба АВСD. Докажите, что четырехугольник РКLM – прямоугольник.
Вариант 2
А1. Диагональ квадрата равна 4 см. Сторона его равна диагонали другого квадрата. Найдите сторону последнего.
А2. Докажите, что середины сторон прямоугольника являются вершинами ромба.
А3. Постройте квадрат по диагонали. Сколько осей симметрии имеет квадрат?
В1. В трапеции АВСD меньшее основание ВС равно 4 см. Через вершину В проведена прямая, параллельная стороне СD. Периметр образовавшегося треугольника равен 12 см. Найдите периметр трапеции.
Контрольная работа №2
Площади фигур
Вариант 1
А1. В прямоугольнике ABCD АВ = 24 см, АС = 25 см. Найдите площадь прямоугольника.
А2. Найдите площадь прямоугольного треугольника, если гипотенуза его равна 40 см, а острый угол равен 60о.
А3. Найдите площадь ромба, если его диагонали равны 14 и 6 см.
А4. Найдите площадь равнобедренной трапеции, у которой высота равна 16 см, а диагонали взаимно перпендикулярны.
В1. Середины оснований трапеции соединены отрезком.
Докажите, что полученные две трапеции равновелики.
Вариант 2
А1. В ромбе ABCD АВ = 10 см, меньшая диагональ АС = 12 см. Найдите площадь ромба.
А2. Найдите площадь равнобедренного треугольника, если его боковая сторона равна 6 см, а угол при вершине равен 60о.
А3. Найдите площадь прямоугольника, если его диагональ равна 13 см, а одна из сторон 5 см.
А4. Найдите площадь равнобедренной трапеции, у которой высота равна 16 см, а диагонали взаимно перпендикулярны.
В1. Докажите, что медиана треугольника разбивает его на два треугольника одинаковой площади.
Контрольная работа №3
Признаки подобия треугольников
Вариант 1
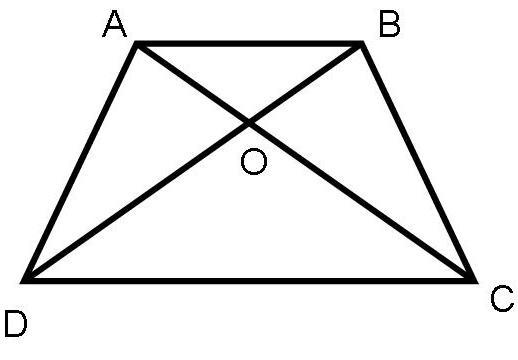
А1. На рисунке АВ || CD.
а) Докажите, что АО : ОС = ВО : OD.
б) Найдите АВ, если OD = 15 см, ОВ = 9 см,
CD = 25 см.
А2. Найдите отношение площадей треугольников ABC и KMN, если АВ = 8 см, ВС = 12 см, АС = 16 см, КМ = 10 см, MN = 15 см, NK = 20 см.
В1. Докажите, что в подобных треугольниках отношение двух сходственных сторон равно отношению двух сходственных высот.
Вариант 2
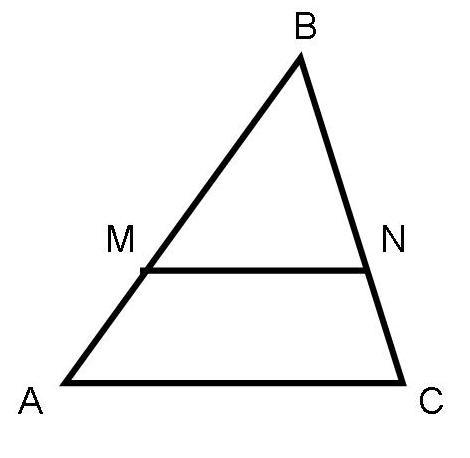
А1. На рисунке MN || АС.
а) Докажите, что  .
.
б) Найдите MN, если AM = 6 см, ВМ = 8 см,
АС = 21 см.
А2. Даны стороны треугольников PКМ и ABC:
PК = 16 см, КМ = 20 см, РМ = 28 см и АВ = 12 см,
ВС = 15 см, АС = 21 см. Найдите отношение площадей этих треугольников.
В1. Докажите, что в подобных треугольниках отношение двух сходственных сторон равно отношению двух сходственных биссектрис.
Контрольная работа №4
Подобные треугольники
Вариант 1
А1. Отрезки АВ и СМ пересекаются в точке О так, что АС || ВМ. Найдите длину отрезка СМ, если АО=12 см, ОВ=3 см, СО=8 см.
А2. В треугольнике АВС точка К принадлежит стороне АВ, а точка Р – стороне АС. Отрезок КР|| BC. Найдите периметр треугольника АКР, если АВ=9 см, ВС=12 см, АС=15 см и АК : КВ=2:1.
А3. В треугольнике АВС угол С=900. АС=15см, ВС=8 см. Найдите 
В1. Между пунктами А и В находится болото. Чтобы найти расстояние между А и В, отметили вне болота произвольную точку С, измерили расстояние АС = 600 м и ВС = 400 м, а также  АСВ = 62°.
АСВ = 62°.
Начертите план в масштабе 1 : 10 000 и найдите по нему расстояние между пунктами А и В.
Вариант 2
А1. Отрезки АВ и СМ пересекаются в точке О так, что АС || ВМ. Найдите длину отрезка СМ, если АС=15 см, ВМ=3 см, СО=10 см.
А2. В треугольнике АВС точка К принадлежит стороне АВ, а точка Р – стороне АС. Отрезок КР|| BC. Найдите периметр треугольника АКР, если АВ=16 см, ВС=8 см, АС=15 см и АК =4 см.
А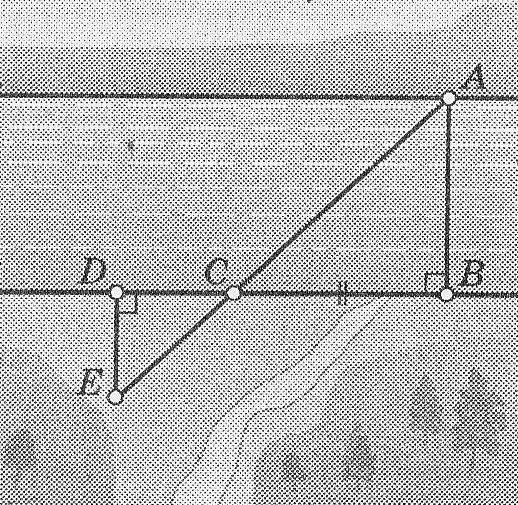 3. В треугольнике АВС угол С=900. АС=4 см, АВ=5 см. Найдите
3. В треугольнике АВС угол С=900. АС=4 см, АВ=5 см. Найдите 
В1. На рисунке показано, как можно определить ширину реки АВ, построив на местности подобные треугольники. Обоснуйте: какие построения выполнены; чем мы пользуемся для определения ширины реки? Выполните необходимые измерения и определите ширину реки
(масштаб рисунка 1 : 1000).
Контрольная работа №5
Окружность
Вариант 1
А1. Из точки данной окружности проведены диаметр и хорда, равная радиусу. Найдите угол между ними.
А2. Хорда АВ стягивает дугу, равную 125о, а хорда АС – дугу в 52о. Найдите угол ВАС
А3. Постройте окружность, описанную около тупоугольного треугольника.
В1. Основание равнобедренного треугольника равно 18 см, а боковая сторона равна 15 см. Найдите радиусы вписанной в треугольник и описанной около треугольника окружностей.
Вариант 2
А1. Через точку данной окружности проведены касательная и хорда, равная радиусу. Найдите угол между ними.
А2. Хорда АВ стягивает дугу, равную 75о, а хорда АС – дугу в 112о. Найдите угол ВАС
А3. Постройте окружность, вписанную в данный треугольник.
В1. Высота, проведенная к основанию равнобедренного треугольника, равна 9 см, а само основание равно 24 см. Найдите радиусы вписанной в треугольник и описанной около треугольника окружностей.
Контрольная работа №6
Итоговая контрольная работа за курс геометрии 8 класса
Вариант 1
А1. В прямоугольном треугольнике найдите гипотенузу с, если его катеты равны: а=5 см, b=12 см.
А2. В треугольнике АВС  . Найдите
. Найдите  .
.
А3. В равнобедренном треугольнике боковая сторона равна 10 дм и основание равно 12 см. Найдите: а)высоту треугольника, проведенную к основанию треугольника; б) площадь треугольника.
А4. Постройте равнобедренный треугольник по боковой стороне и углу при основании.
В1. Около остроугольного треугольника АВС описана окружность с центром О. Расстояние от точки О до прямой АВ равно 6 см,  .
.
Найдите: а) угол АВО; б) радиус окружности.
Вариант 2
А1. В прямоугольном треугольнике гипотенуза с=25 см, один из его катетов: а=24 см. Найдите другой катет b.
А2. В прямоугольном треугольнике АВС  . Найдите
. Найдите  .
.
А3. В равнобедренном треугольнике боковая сторона равна 13 дм и основание равно 10 см. Найдите: а)высоту этого треугольника, проведенную к основанию треугольника; б) площадь треугольника.
А4. Постройте окружность данного радиуса, проходящую через две данные точки.
В1. В треугольник АВС с прямым углом С вписана окружность с центром О, касающаяся сторон АВ, ВС и СА в точках DE и F соответственно. Известно, что  .
.
Найдите: а) радиус окружности; б) углы EOF и EDF.
СОГЛАСОВАНО
Протокол заседания школьного
Методического объединения учителей
естественно-математического цикла
от «____» ___________2019г № ____
СОГЛАСОВАНО
Заместитель директора по УВР
________________ О.Н.Гамзина
«____» ________________ 2019 г








 А = 30о, а перпендикуляр ВН к прямой АD равен 7,5 см. Найдите стороны параллелограмма
А = 30о, а перпендикуляр ВН к прямой АD равен 7,5 см. Найдите стороны параллелограмма

 .
.
 АСВ = 62°.
АСВ = 62°.  3. В треугольнике АВС угол С=900. АС=4 см, АВ=5 см. Найдите
3. В треугольнике АВС угол С=900. АС=4 см, АВ=5 см. Найдите  . Найдите
. Найдите  .
. .
.  . Найдите
. Найдите  .
. 









