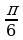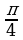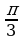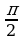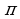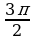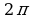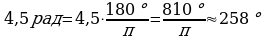Предмет: Алгебра Класс: 10 Дата_____ Номер урока____
Тема урока: «Радианная мера углов».
Цели урока:
1) учебные:
дать понятие о радианном измерении углов,
изучить связь между градусной и радианной мерами измерения углов,
познакомиться с формулами перевода градусной меры в радианную меру и наоборот,
получить представление о вычисление длины дуги с использование значений углов в радианах,
научиться применять формулы, изученные на уроке для решения задач и упражнений.
2) развивающие:
получение учащимися представлений о появлении тригонометрии как науки, о её практическом применении,
развитие навыков абстрактного мышления,
развитие представлений о разностороннем подходе к решению задач,
воспитывающие: активизировать интерес к изучаемому материалу.
Ход урока.
1.Организационный момент. Проверка готовности к уроку.
2. Мотивация урока.
Проверяется подготовленность классного помещения и готовность учащихся к уроку.
Сегодня у нас первый урок нового для нас раздела математики – тригонометрии. С отдельными тригонометрическими понятиями вы уже могли встречаться на уроках геометрии и алгебры в 8-9 классах. Но полноценное знакомство с этой наукой мы начинаем именно сегодня.
В древности люди следили за светилами и по этим наблюдениям вели календарь, рассчитывали сроки сева, время разлива рек; корабли на море, караваны на суше ориентировались в пути по звездам. Все это привело к потребности научиться вычислять стороны в треугольнике, две вершины которого находятся на земле, а третья представляется точкой на звездном небе. Исходя из этой потребности и возникла наука – тригонометрия – наука, изучающая связи между сторонами в треугольнике.
Как вы думаете, достаточно ли уже известных нам соотношений для решения таких задач?
Цель сегодняшнего урока – исследовать новые связи и зависимости, вывести соотношения, применяя которые на следующих уроках геометрии, вы сможете такие задачи решать.
Давайте почувствуем себя в роли научных работников и вслед за гениями древности Фалесом, Евклидом, Пифагором пройдем путь поиска истины. Для этого нам нужна теоретическая база.
3. Актуализация опорных знаний. Проверка д/з.
Что называется углом? виды углов, единицы измерения. Транспортир. Построение углов.
1°=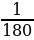 часть развернутого угла.
часть развернутого угла.
Синусом острого угла прямоугольного треугольника называется… отношение противолежащего катета к гипотенузе.
Косинусом острого угла прямоугольного треугольника называется… отношение прилежащего катета к гипотенузе.
Тангенсом острого угла прямоугольного треугольника называется… отношение противолежащего катета к прилежащему катету.
4. Изучение нового материала.
Просмотр презентации. Творческое задание.
В тригонометрии угол-это фигура, образованная при повороте луча на плоскости около начальной точки. Работа с учебником с.234.
Измерение углов.
Каждому углу как фигуре ставится в соответствие угол поворота, с помощью которого образован этот угол.
Направление поворота против часовой стрелки положительное, а по часовой стрелке - отрицательное. Выполнить задание 1 (нечетные) с.238.
В математике и физике. Кроме градусной меры углов. Используется радианная мера.
Углом в один радиан называют центральный угол, которому соответствует длина дуги, равная длине радиуса окружности.
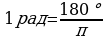 ;
; 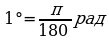 ;
; 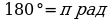 ;
; 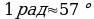
Переход от градусной меры углов к радианной
Найдём радианную меру угла72 °
Так как 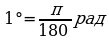 , то
, то 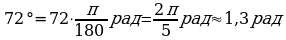
При записи радианной меры угла, обозначение «рад» часто опускают.
Например: 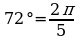 .
.
Заполнить таблицу:
| α °
α рад | 0°
0 | 30°
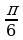 | 45°
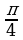 | 60°
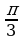 | 90°
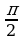 | 180°
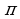 | 270°
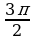 | 360°
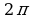 |
Переход от радианной меры углов к градусной
Выразим в градусах 4,5 рад.
Так как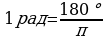 , то
, то 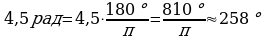
Историческая пауза.
В IV-V веках появился уже специальный термин в трудах по астрономии великого индийского учёного Ариабхаты, именем которого назван первый индийский спутник Земли. Дугу он назвал ардхаджива (ардха – половина, джива – тетива лука, которую напоминает хорда). Позднее появилось более краткое название джива. Арабскими математиками в IX веке это слово было заменено на арабское слово джайб (выпуклость). При переводе арабских математических текстов в веке оно было заменено латинским синус (sinus – изгиб, кривизна).
Слово косинус намного моложе. Косинус – это сокращение латинского выражения completely sinus, т. е. “дополнительный синус” (или иначе “синус дополнительной дуги”; cosa = sin( 90° - a)).
Название «тангенс», происходящее от латинского tanger (касаться), появилось в 1583 г. Tangens переводится как «касающийся» (линия тангенсов – касательная к единичной окружности).
Термин «тригонометрия» означает дословно треугольникомерие или измерения в треугольнике.
5. Закрепление нового материала.
Решение у доски: пример 1, 2 с.236, 2, 4 (нечетные)
6. Повторение. Понятие множества.
7. Итоги урока. Рефлексия. Д\З.






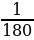 часть развернутого угла.
часть развернутого угла.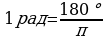 ;
; 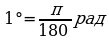 ;
; 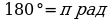 ;
; 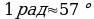
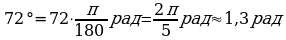
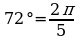 .
.