Тема: Решение примеров на нахождение производных функций
Задание 1. Самостоятельная работа
В.1 В.2
Найдите производные функций:
1. у = х4 – 4х3 – 8х2 + 13 1. у = 2х7 – 3х5 – х - 10
2. у = 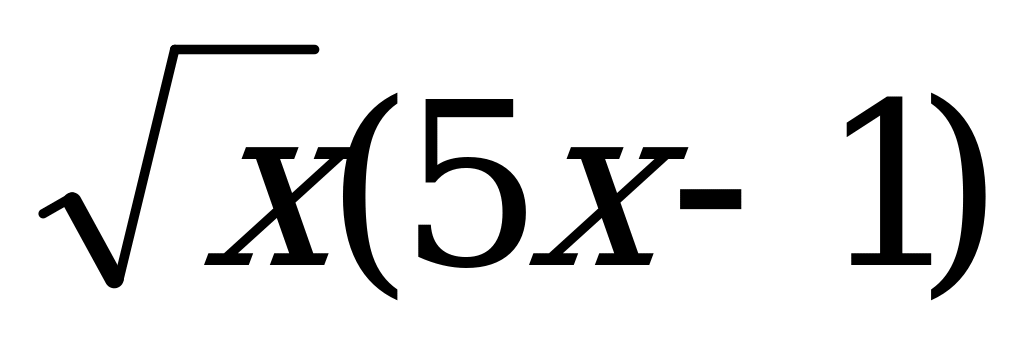 2. у =
2. у = 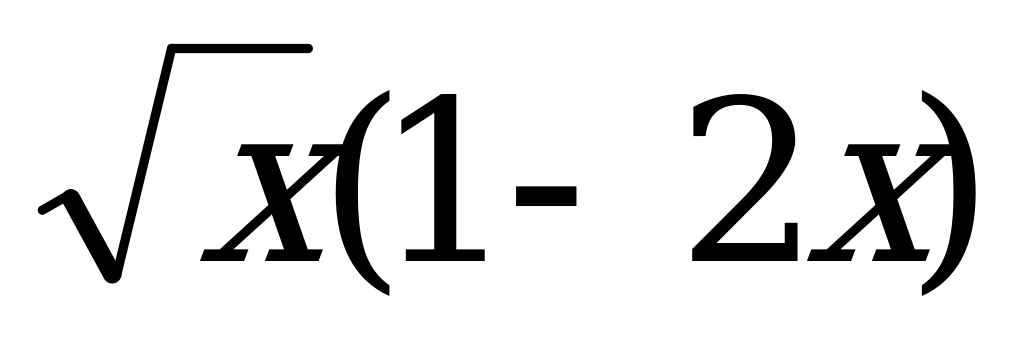
3. у = 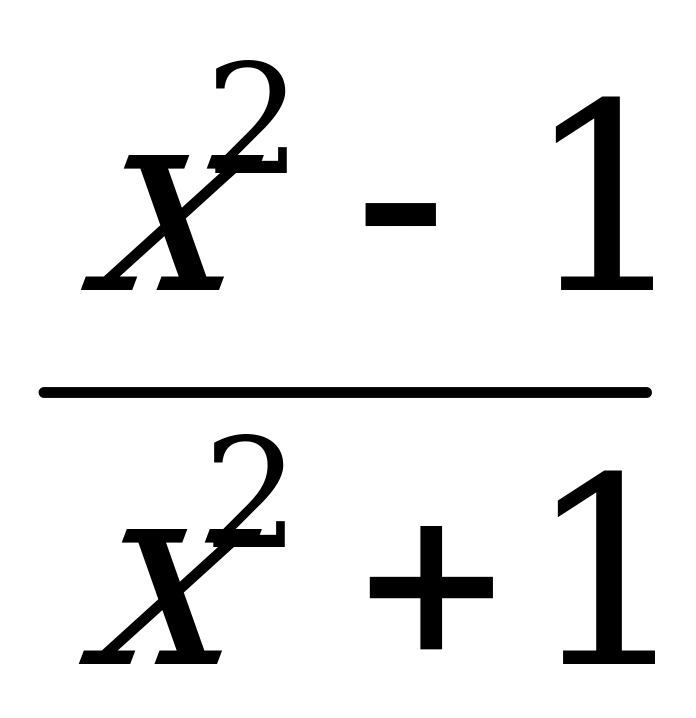 3. у =
3. у = 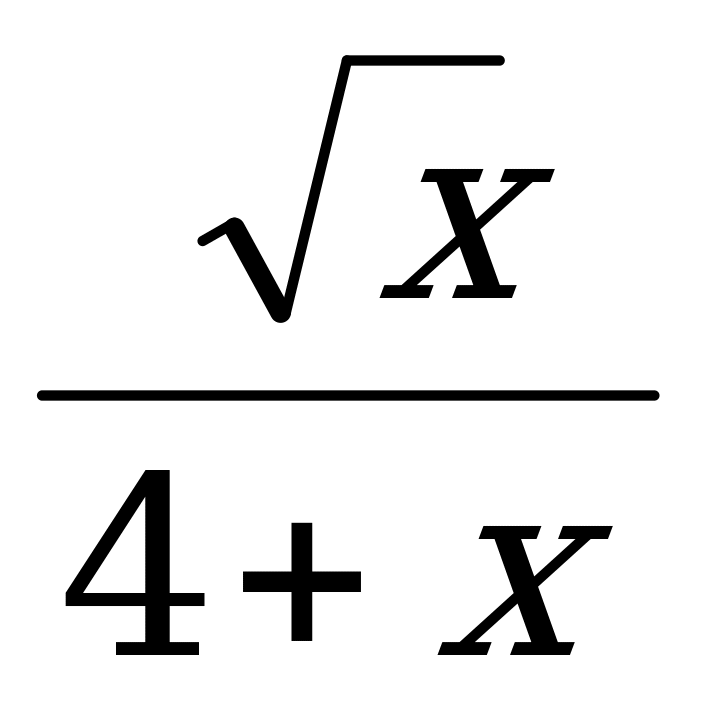
Задание 2. Найти значения х, при которых производная функции f равна нулю:
а) f(x) = х5 – 3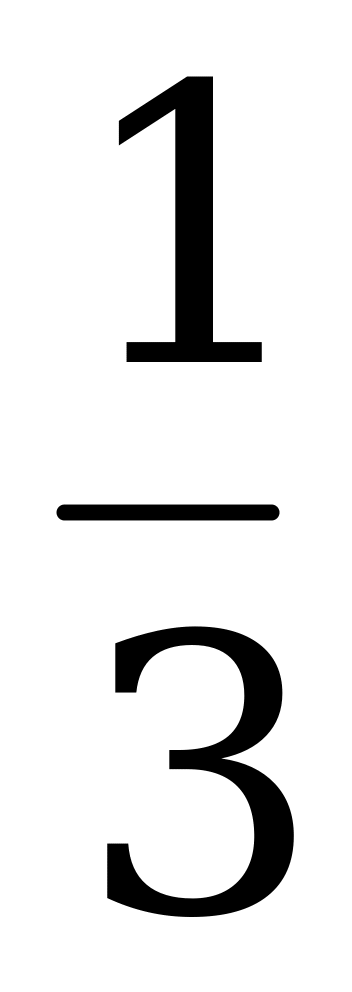 х3 + 5х в) f(x) = х4 + 4х
х3 + 5х в) f(x) = х4 + 4х
б) f(x) = 2х4 –х8 г) f(x) = х4 –12х2
Задание 3. Решить неравенство f / (х)
а) f(x) = х3 –6х2 - 63х в) f(x) = 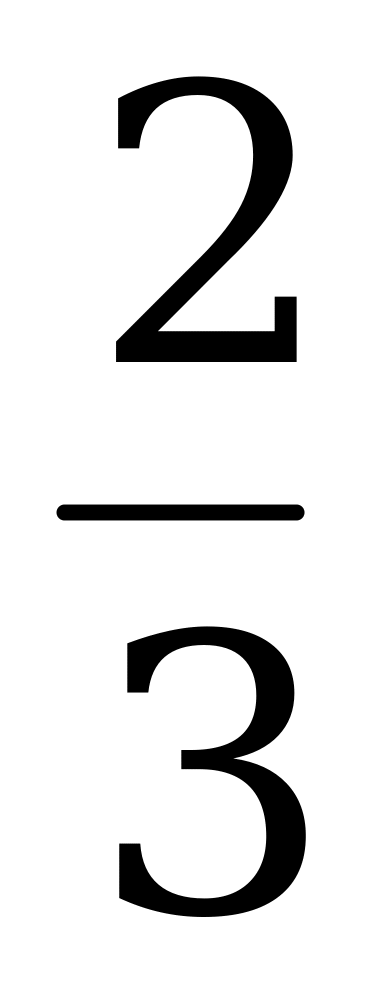 х3 - 8х
х3 - 8х
б) f(x) = 3х -5х2 + х3 г) f(x) = 3х2 – 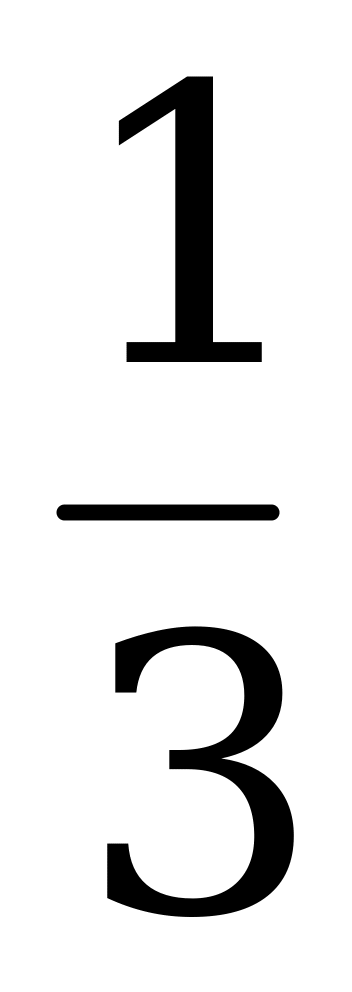 х3 - 9х
х3 - 9х
Задание 4. Задайте формулой хотя бы одну функцию, производная которой равна:
а) f(x) = 16х3 –0,4 в) f(x) = 8х – 2 д) f(x) = 2cos2х
б) f(x) = 9х2 – 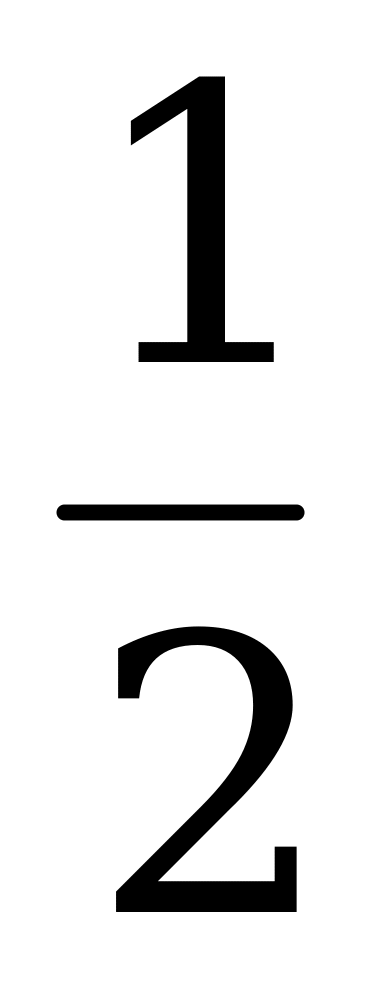 г) f(x) = 1 – sinх е) f(x) = 3sinх
г) f(x) = 1 – sinх е) f(x) = 3sinх
Задание 5. Найти производные функций:
1) у = 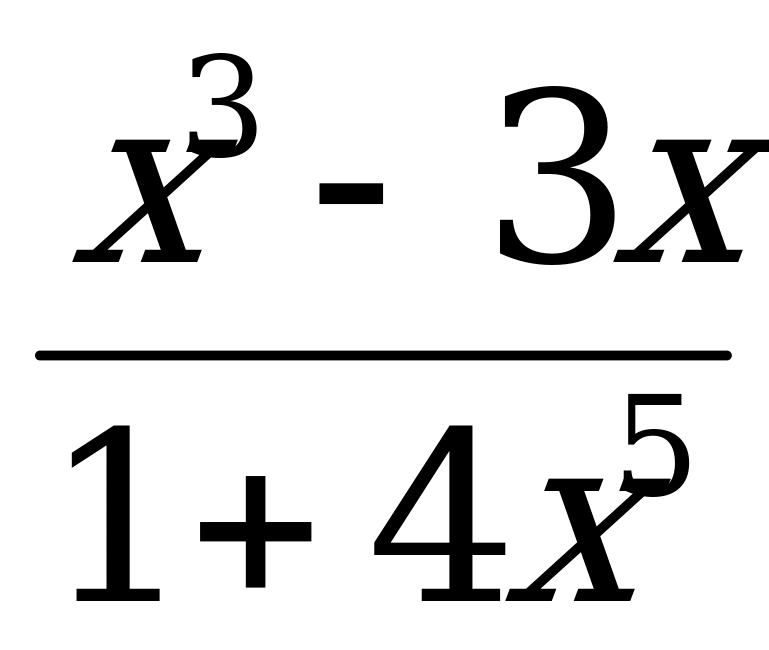 2) у =(
2) у =( 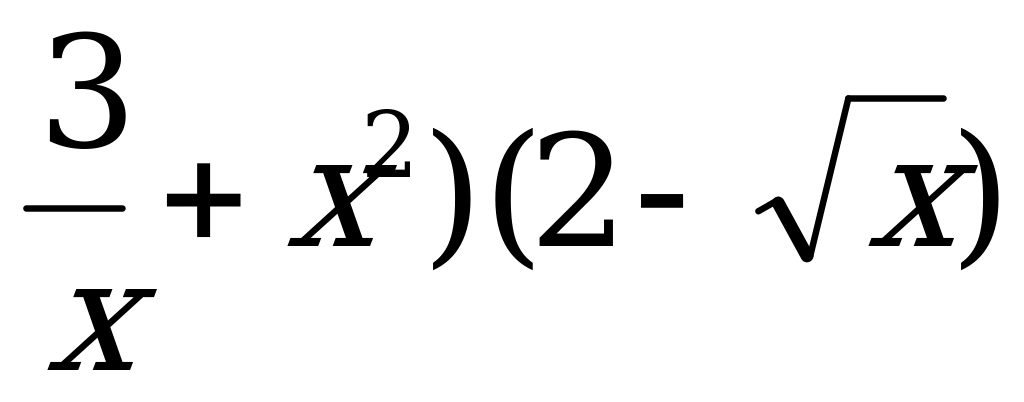
3) у = (2х – 7)8 4) у = (9х + 5)4
5) у = (х3 – 2х2 + 3)17 6) у = 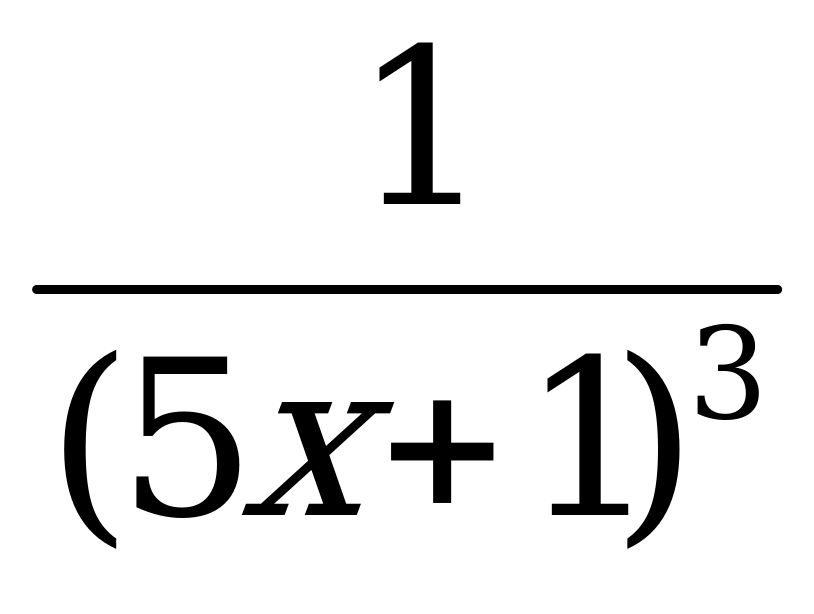
7) у = (3 - 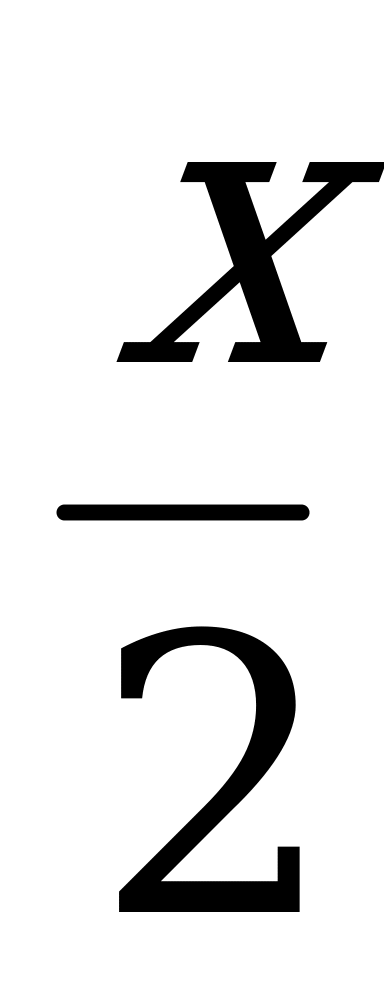 )-9 8) у =
)-9 8) у = 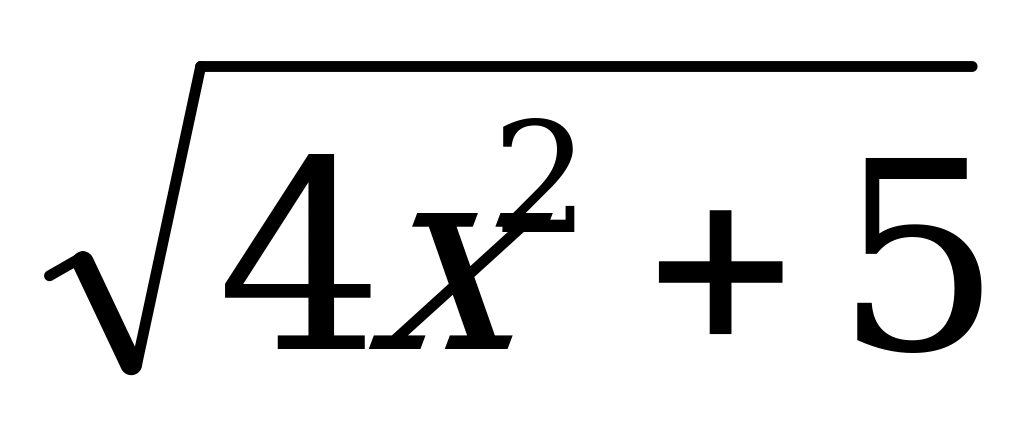
9) у = 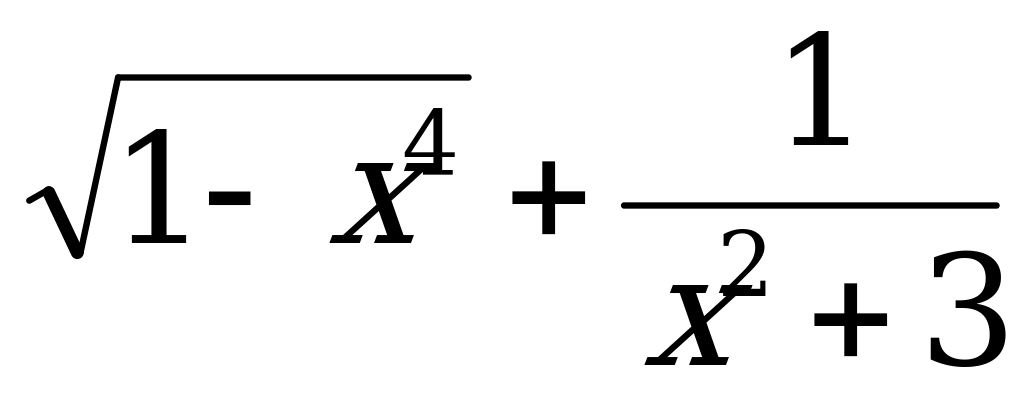 10) у = ( 3 – х3)5 +
10) у = ( 3 – х3)5 +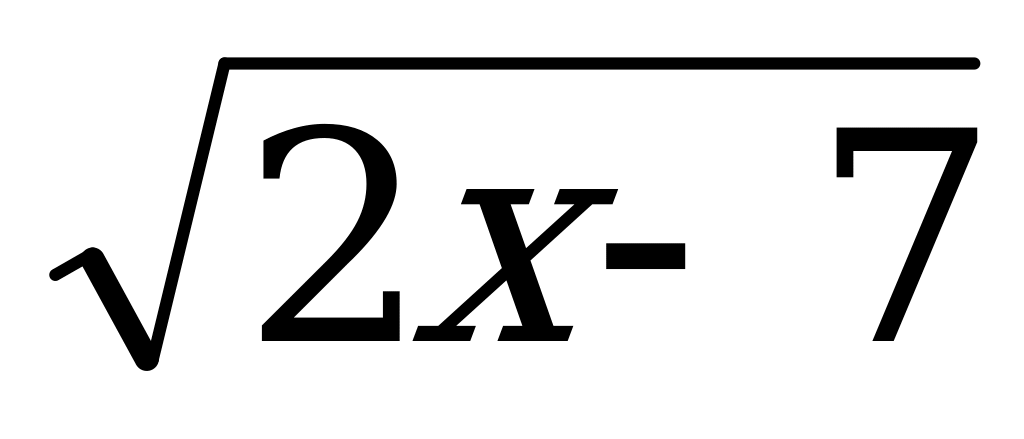
11) у = х3sin2х 12) у = 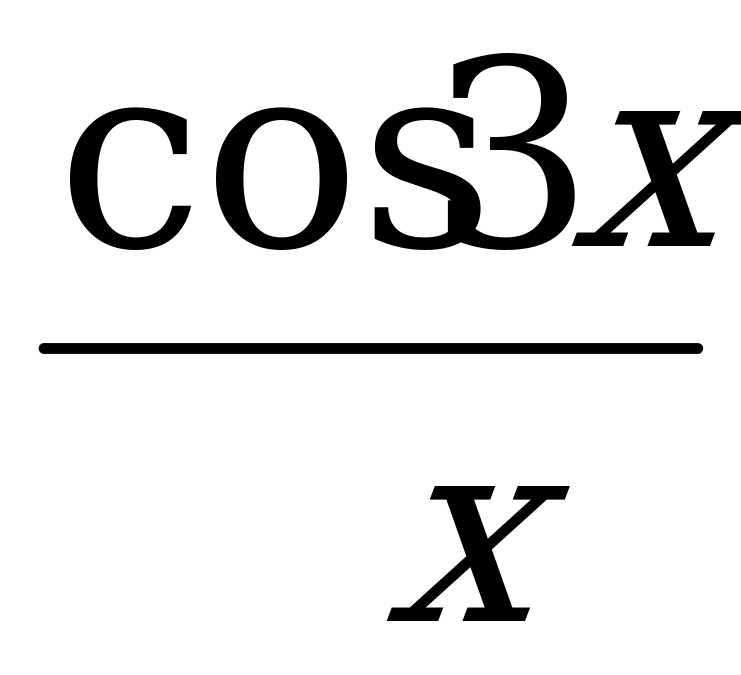
13) у = х4 + tg2х 14) у = sin2х
15) у = sin2х + cos2х 16) у =cos2хsinx + sin2xcosx
17) y = sin3xcos3x
Задание 6. Вычислить значения производных функций при заданных значениях аргумента:
а) f(х) = (3х2 – 7х + 2)(1 – 2х – 5х2), х0 = 1 в) f(х) = 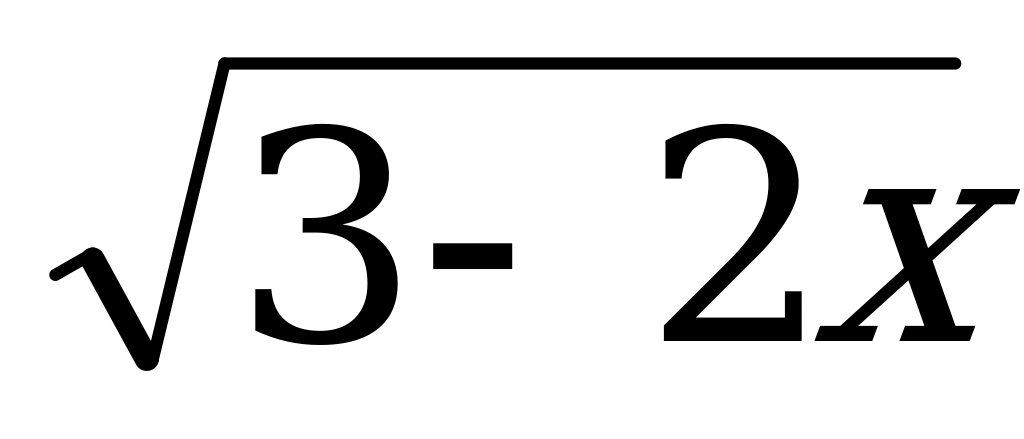 , х0 = 1
, х0 = 1
б) f(х) = 3 - sin2х, х0 = 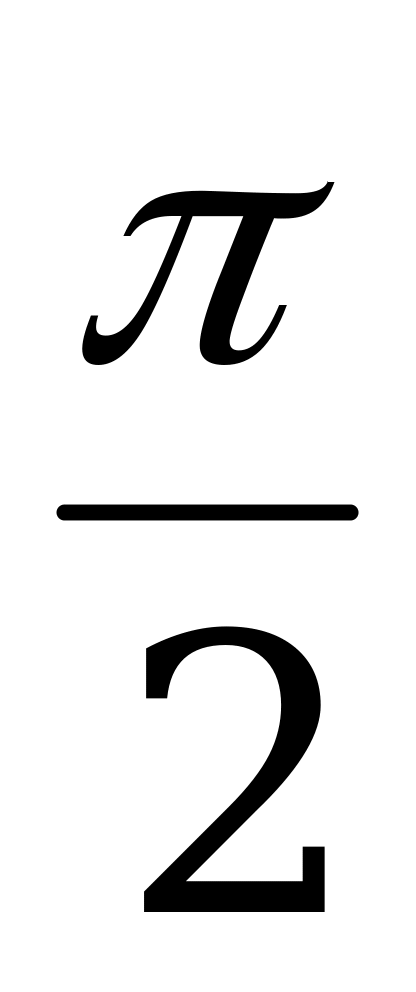 г) f(х) =
г) f(х) = 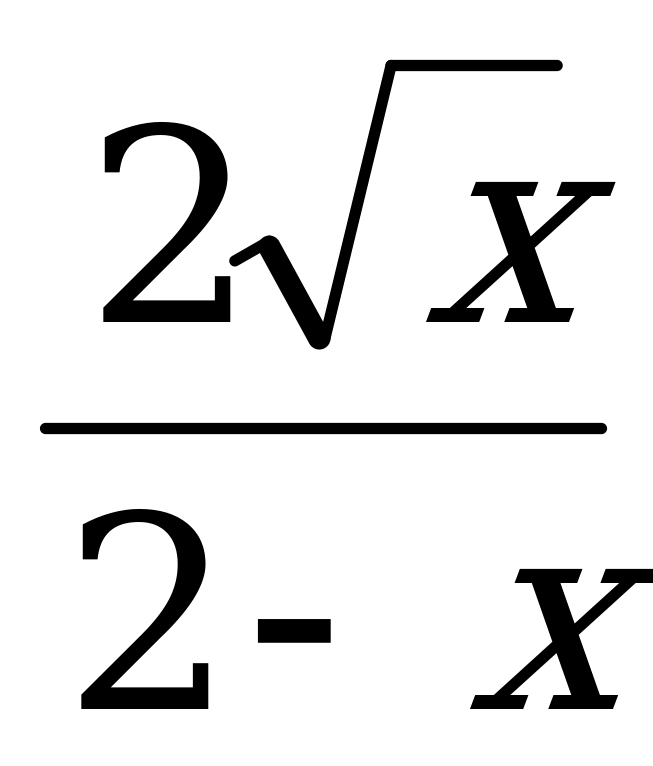 , х0 = 1
, х0 = 1
Тема:
Экстремум функции. Исследование функции на экстремум.
1. Найти промежутки возрастания и убывания функции:
а) f(х) = 3 - 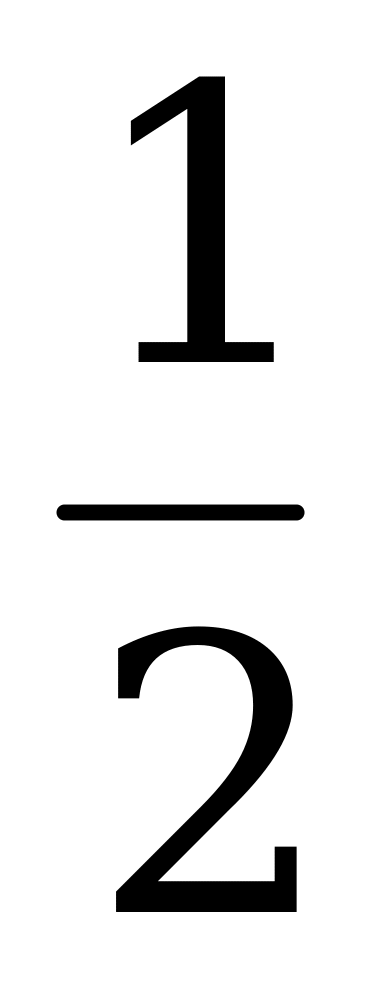 х б) f(x) = - x2 + 2x – 3 в) f(x) = 4х – 5
х б) f(x) = - x2 + 2x – 3 в) f(x) = 4х – 5
г) f(x) = 5х2 – 3х + 1 д) f(x) = х2 (х – 3) е) f(x) = x3 - 27x
ж) f(x) =12х + 3x2 - 2x3 з) f(x) = 4 – x4 и) f(x) = х (х2 – 12).
2. Исследовать функцию на экстремум:
а) f(x) = 4 – 2х + 7х2 б) f(x) = 5 + 12х – х3
в)f(x) = 4х - 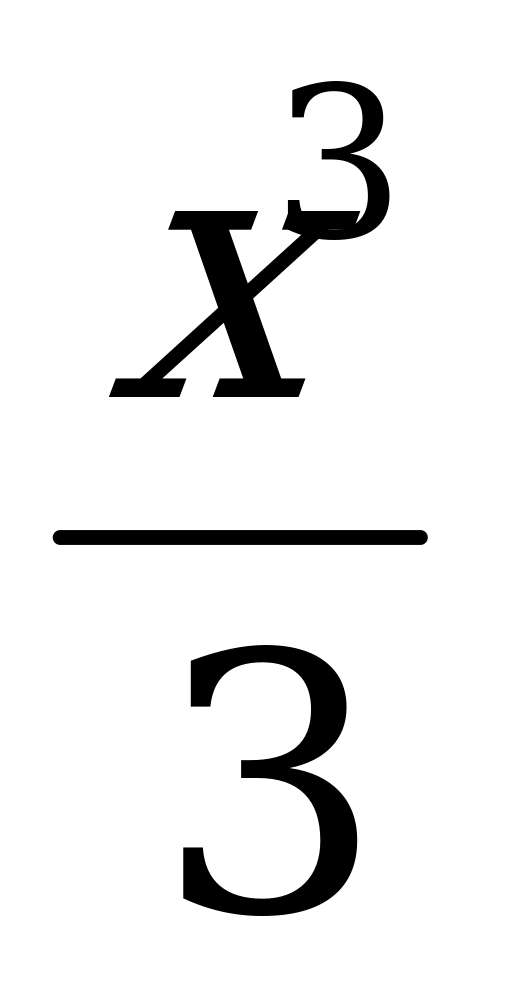 г) f(x) = 2х3 + 3х2 – 4
г) f(x) = 2х3 + 3х2 – 4
д) f(x) = 9 + 8х2 – х4 е) f(x) = 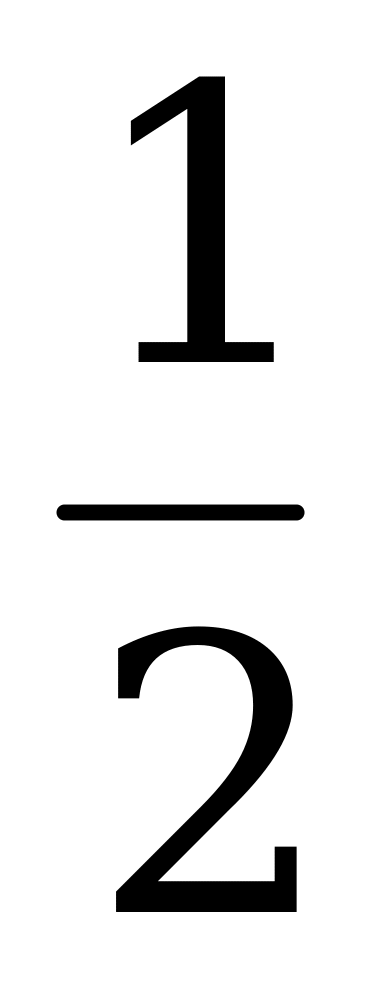 х4 – х2
х4 – х2
ж) f(x) = х3 – 4х + 8 з) f(x) = х4 – 18х2 +5.
Тема: Исследование функции и построение графика функции
1. Самостоятельная работа
В.1. В.2.
Дана функция
у = х3 – 3х2 + 4 у = 0,5х4 – 4х2
Найдите:
а) промежутки возрастания и убывания функции
б) точки экстремума.
Общая схема исследования функции и построение ее графика:
1. Найти область определения и область значений функции.
2. Исследовать функцию на четность.
3. Исследовать функцию на периодичность.
4. Определить точки пересечения графика функции с осями координат и промежутки
знакопостоянства.
5. Определить промежутки возрастания и убывания функции.
6. Определить точки экстремума функции и значения функции в этих точках.
7. Построить график функции.
2. Исследуйте функцию и постройте ее график:
а) f(x) = х2 – 2х + 8 б) f(x) = - х2 + 5х + 4 в) f(x) = - х3 + 3х – 2
г) f(x) = х3 + 3х + 2 д) f(x) = х4 – 2х2 – 3 е) f(x) = 3х2 – х3
ж) f(x) = х4 – 2х2 – 3 з) f(x) = 6х – 2х3 и) f(x) = 2х3 – 3х2
к) f(x) = 5х3 – 3х5 л) f(x) = х4 + 2х3 – 5х2.
3. Найти промежутки возрастания и убывания функции:
а) у = 1 + 1,5х – 3х2 – 2,5х3 б) у = 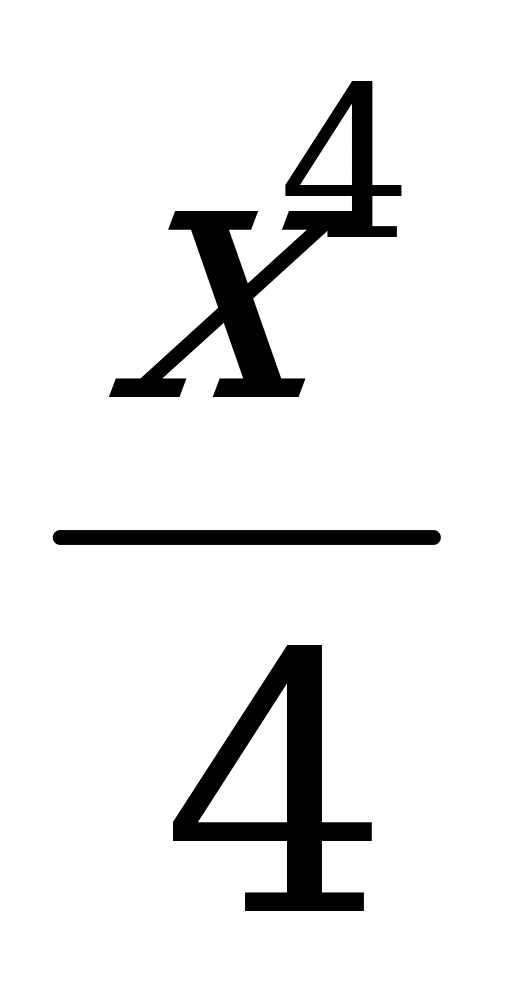 + 8х – 5
+ 8х – 5
в) у = 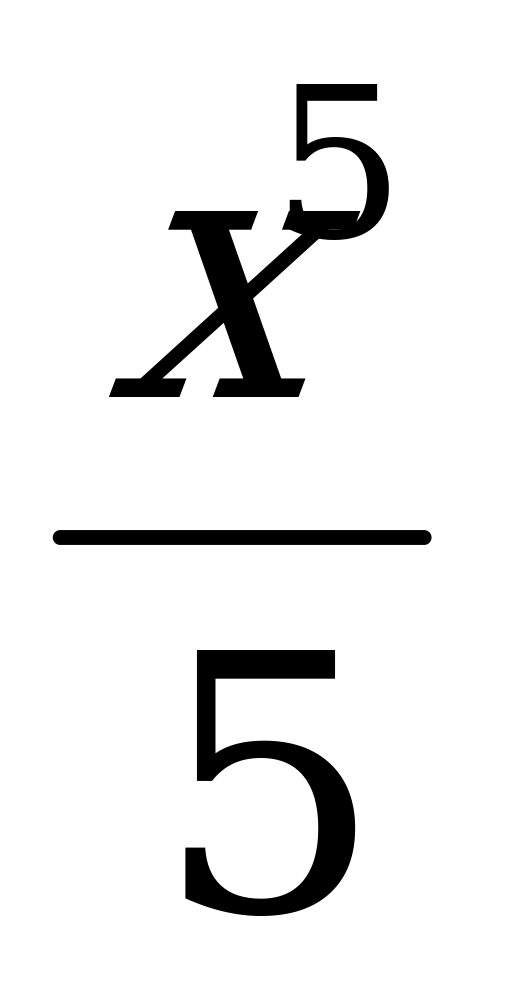 -
- 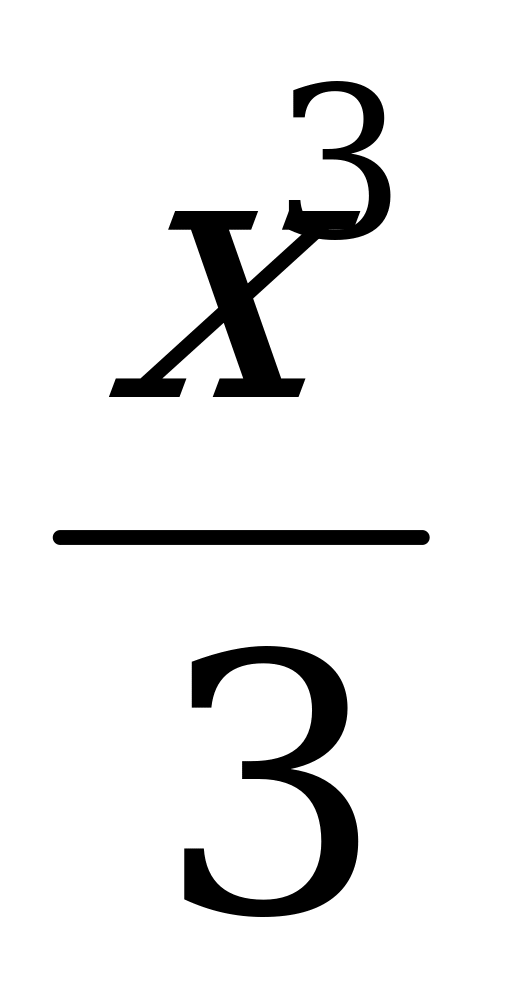 - 6х +1 г) у = х3 – 6х2 – 15х – 2.
- 6х +1 г) у = х3 – 6х2 – 15х – 2.
Экстремум функции. Исследование функции на экстремум.
1. Промежутки монотонности функции
Одной из основных задач исследования функции является нахождение промежутков ее возрастания и убывания. такое исследование легко проводить с помощью производной. Сформулируем соответствующие утверждения.
Определение:. Промежутки монотонности функции у = f(x) - это промежутки, в которых функция возрастает или убывает.
Теорема (о монотонности функции): Если функция f(х) во всех точках некоторого интервала имеет положительную производную (f (х) 0), то она возрастает на этом интервале, а если имеет отрицательную производную (f (х)
Пример 1. Найти промежутки монотонности функции у = 5х2 -3х +1.
Область определения функции D(f) = R. Производная данной функции равна:
f (х) = 10х – 3.
f (х) 0: 10х – 3 0, х 0,3
f (х)
Значит на промежутке (- ; 0,3] функция убывает, а на промежутке [ 0,3; + ) функция возрастает. (Точка х = 0,3 включается в промежутки монотонности, т.к. в этой точке функция определена и непрерывна).
2. Критические точки функции
Пример 2. Найти промежутки монотонности функцииf(x) = х – х2
f (х) = 1 – 2х
f (х) 0: 1- 2х 0, х ; 0,5].
f (х) 0,5. Функция убывает на [ 0,5; + ).
Если функция непрерывна в каком-либо из концов промежутка, то эту точку присоединяют к этому промежутку.
Точка х = 0,5 – это внутренняя точка области определения функции, в которой производная равна нулю. Такая точка называется критической точкой функции.
Точки, в которых производная равна нулю или не существует, разбивают область определения функции на промежутки, в каждом из которых f (х) сохраняет постоянный знак. поэтому для нахождения промежутков возрастания (убывания) удобно пользоваться обобщением метода интервалов.
Определение: Внутренние точки области определения функции, в которых ее производная равна нулю или не существует, называются критическими точками этой функции.
Правило нахождения промежутков возрастания (убывания) функции:
1. Найти производную функции f (х).
2. Найти критические точки функции, решив уравнение: f (х) = 0.
3. Найти знак производной на каждом интервале.
4. Согласно теореме о монотонности функции, найти промежутки возрастания и убывания функции.
Пример 3. Найти промежутки монотонности функции у = 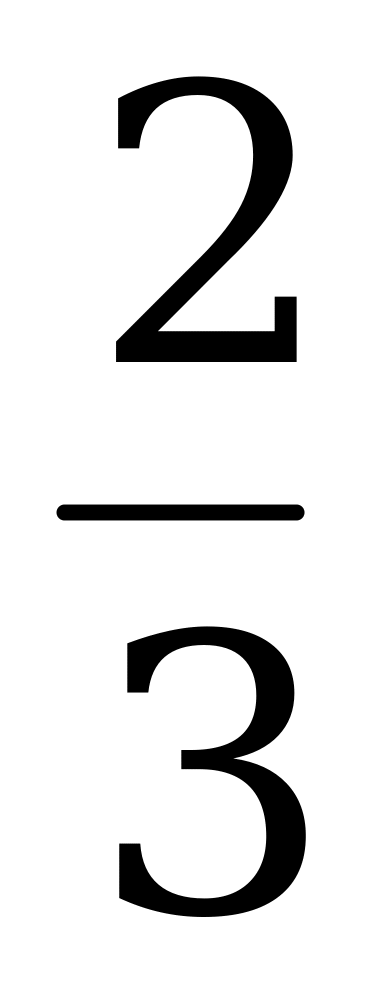 х3 – 2х + 1.
х3 – 2х + 1.
Данная функция определена и дифференцируема на всей числовой прямой: D(f) = R.
Найдем ее производную: f (х) = 2х2 – 2 = 2(х2 – 1) = 2(х – 1)(х + 1).
Решив уравнение f (х) = 0: 2(х – 1)(х + 1) = 0, найдем критические точки: х = 1 и
х = - 1. Используя метод интервалов, определим знаки производной на каждом интервале:
f (х)
f(x) 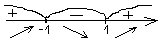
По теореме о монотонности функции данная функция возрастает на (- ; - 1] [ 1; + ) и убывает на [ -1; 1].
3. Исследование экстремумов функции
Определение: Точка х0 называется точкой минимума функции f(x), если существует такая окрестность точки х0, что для всех х х0 из этой окрестности выполняется неравенство: f(x) ≥ f(x0).
Определение: Точка х0 называется точкой максимума функции f(x), если существует такая окрестность точки х0, что для всех х х0 из этой окрестности выполняется неравенство: f(x) f(x0).
Определение: Точки максимума и минимума функции называются точками экстремума данной функции, а значения функции в точках максимума и минимума называются максимумом и минимумом функции или экстремумами функции.
Теорема ( об экстремумах дифференцируемой функции): Для того, чтобы функция у = f(x) имела в точке х0 экстремум, необходимо, чтобы f (х0) = 0 , и достаточно, чтобы
f (х) меняла знак при переходе через точку х0 (если слева от х0 имеем f (х)f (х) 0, то в точке х0 будет минимум, если наоборот – то максимум).
Правило нахождения экстремумов функции:
1. Найти критические точки функции f(x), т.е. точки, в которых производная функции f (х) равна нулю или не существует.
2. Исследовать знак производной f (х) в некоторой окрестности каждой критической точки. При этом, если f (х) меняет знак при переходе через такую точку, то функция f(x) в этой точке имеет экстремум. Т.е. если знак меняется с - на + , то в этой точке минимум, если с + на - , то в этой точке максимум. Если же знак f (х) не меняется при переходе через рассматриваемую точку, то функция f(x) не имеет экстремума в этой точке.
Пример 4. Найти экстремумы функции f(x) = 2х3 – 3х2 – 2.
1. Находим критические точки: f (х) = 6х2 – 6х, 6х2 – 6х = 0, 6х(х – 1) = 0, х = 0 и
х = 1.
2. Эти точки х = 0 и х = 1 разбивают область определения функции на три интервала. Определим знак производной на каждом из интервалов:
f (х) max min
f(x) 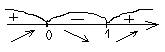
Следовательно, в точке х = 0 – max: f(0) = - 2
в точке х = 1 – min: f(1) = - 3.

















