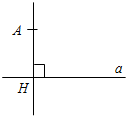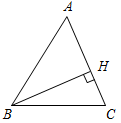Разработка урока геометрии по теме «Перпендикуляр к прямой. Медианы, биссектрисы и высоты треугольника»

Цель деятельности учителя

Создать условия для введения понятий перпендикуляра к прямой, медианы, биссектрисы и высоты треугольника, доказательства теоремы о перпендикуляре, обучения построению медианы, биссектрисы и высоты
треугольника

Термины и понятия

Треугольник, медиана, биссектриса, высота, перпендикуляр

Планируемые результаты

Предметные умения

Универсальные учебные действия

Научатся различать понятия медианы, высоты и биссектрисы треугольника, перпендикуляра к прямой.

Познавательные: научиться владеть логическими действиями определения понятий, обобщения, установления аналогий; научиться устанавливать причинно-следственные связи, строить логическое рассуждение, умозаключение.

Регулятивные: научиться самостоятельно планировать альтернативные пути достижения целей.

Коммуникативные: научиться организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками.

Личностные: проявляют познавательный интерес к изучению предмета

Организация пространства

Формы работы

Фронтальная (Ф); парная (П); индивидуальная (И)

Образовательные
ресурсы

• Задания для фронтальной, парной и индивидуальной работы.

Мультимедийная презентация.

I этап. Актуализация знаний учащихся

Цель деятельности

Совместная деятельность

Входной контроль

(Ф/И)

1. Выполнение заданий входного контроля.

2. Проверить готовность к уроку.

II этап. Учебно-исследовательская деятельность

Цель деятельности

Совместная деятельность

Ввести понятия
медианы, биссектрисы и высоты треугольника в ходе практической
деятельности

(Ф/И)

1. Выполнение практического задания.

– Начертите прямую а и отметьте точку А, не лежащую на прямой (рис. 1).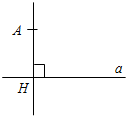

Рис. 1

– Через точку А проведите прямую, перпендикулярную прямой а. Точку пересечения прямых обозначьте Н.

– Запишите в тетрадях: «Отрезок АН – перпендикуляр, проведенный из точки А к прямой а, если: 1) АН  а;

2) А  а, Н  а».

Теорема о перпендикуляре: Из точки, не лежащей на прямой, можно провести перпендикуляр к этой прямой и притом только один.

Дано: а – прямая, точка А  а.

Доказать: 1) из точки А к прямой а можно провести перпендикуляр;

2) из точки А к прямой а можно провести единственный перпендикуляр.

Доказательство: см. п. 16 учебника.

2. Определение: Отрезок, соединяющий вершину треугольника с серединой противолежащей стороны, называется медианой треугольника.

На доске и в тетрадях рисунок (рис. 2) и запись: AM – медиана ∆АВС, если М  ВС, ВМ = МС.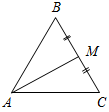

Рис. 2

– Начертите ∆MNK, постройте его медианы. (На доске это же задание выполняет один из учащихся по указанию учителя.)

На доске и в тетрадях рисунок (рис. 3) и запись: MB, KA, NC – медианы ∆MNK. MB  KA  NC = О.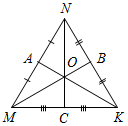

Рис. 3

3. Определение: Отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны, называется биссектрисой треугольника.

На доске и в тетрадях рисунок (рис. 4) и запись: BL – биссектриса ∆АВС, если L  АС, ABL = CBL.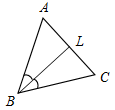

Рис. 4

– Начертите ∆DEF, постройте его биссектрисы. (На доске это же задание выполняет один из учащихся по указанию учителя.)

На доске и в тетрадях рисунок (рис. 5) и запись: DN, EK, FM – биссектрисы ∆DEF. DN  ЕK  ЕМ = О.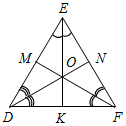

Рис. 5

4. Определение: Перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону, называется высотой треугольника.

На доске и в тетрадях рисунок (рис. 6) и запись: ВН – высота ∆АВС, если ВН  АС, Н  АС.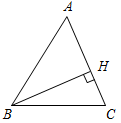

Рис. 6

– Начертите остроугольный, прямоугольный и тупоугольный треугольники и постройте их высоты.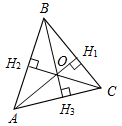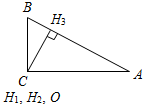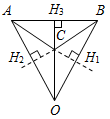

Рис. 7 Рис. 8 Рис. 9

(К доске вызвать трех учеников, первый из них строит высоты для остроугольного треугольника, второй – для прямоугольного, третий – для тупоугольного.)

III этап. Решение задач на закрепление изученного материала

Цель деятельности

Деятельность учителя

Деятельность учащихся

Совершенствовать навыки построения медиан, биссектрис и высот;

научиться организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками.

(П) Выполнить задание в парах

Выполняют задания на листочках для закрепления понятий.

IV этап. Итоги урока. Рефлексия

Деятельность учителя

Деятельность учащихся

(Ф/И)

- Заполните пропуски в определениях и теоремах.

– Какими свойствами обладают медианы, биссектрисы и высоты треугольника?

(И) Работа с раздаточным материалом, проверка с помощью презентации.

(И) Домашнее задание: изучить пункты 16 и 17; ответить на вопросы 5–9 на
с. 50; выполнить № 100-103