Сценарий урока в 6 классе по теме «Решение уравнений»
Цель урока: создание условий для получения и осмысления учениками новых знаний о способах решения уравнений, систематизация теоретического материала по указанной теме, отработка навыка решения уравнений различными методами; умение работать по алгоритму.
Целевые установки на достижение планируемых результатов:
- личностные: умение слушать и вступать в диалог, участвовать в обсуждении проблем, содействовать формированию и развитию нравственных, трудовых, эстетических качеств личности учащихся (дисциплинированность, ответственность, аккуратность, радость и сопереживание их успехам), формировать коммуникативную компетенцию учащихся;
- метапредметные: способствовать развитию устной и письменной речи, изложению своих мыслей с применением математической терминологии, обогащению ее словарного запаса, самостоятельного мышления, навыка самооценки, самопроверки и ведения записей в собственной тетради;
- предметные: создать условия для понимания алгоритма решения уравнений и использования свойств уравнений.
Задачи:
Образовательные (формирование познавательных УУД):
повторить решение уравнений на нахождение неизвестного множителя, закрепить примеры равносильных преобразований уравнений, алгоритм решения уравнения, используя перенос слагаемых из одной части уравнения в другую; извлекать необходимую информацию из прослушанного материала; структурировать информацию в виде записи выводов и определений.
Воспитательные (формирование коммуникативных и личностных УУД): умение слушать и вступать в диалог; формировать внимательность и аккуратность в вычислениях; воспитывать чувство взаимопомощи, уважительное отношение к чужому мнению, культуру учебного труда, требовательное отношение к себе и своей работе; развивать у учащихся умение работать индивидуально и в группах.
Развивающие (формирование регулятивных УУД): самостоятельно ставить новые учебные задачи путем задавания вопросов о неизвестном; планировать собственную деятельность, определять средства для ее осуществления; способствовать развитию творческой активности учащихся.
Планируемые результаты обучения.
Предметные: уметь в процессе реальной ситуации использовать понятия «уравнение», «равенство», «корень уравнения»; познакомиться со свойствами уравнений; новым способом решения уравнений; отрабатывать умение решать уравнения.
Регулятивные: самостоятельно ставить новые учебные задачи путем задавания вопросов о неизвестном; планировать собственную деятельность, определять средства для ее осуществления.
Познавательные: извлекать необходимую информацию из прослушанного материала; структурировать информацию в виде записи выводов и определений.
Коммуникативные: умение работать в парах, слушать собеседника и вести диалог, аргументировать свою точку зрения; эффективно сотрудничать и способствовать продуктивной кооперации.
Личностные: умение правильно излагать свои мысли, понимать смысл поставленной задачи.
1.Самоопределение к учебной деятельности
Здравствуйте, дорогие ребята! Садитесь! Я рада приветствовать Вас на уроке математики и прошу обратить внимание на доску.
«Учиться надо весело…. Чтобы усваивать знания, надо переваривать их с аппетитом»
А. Франц.
Как вы понимаете это высказывание? Согласны ли вы с ним?
Абсолютно верно! Это высказывание будет девизом нашего сегодняшнего урока!
2. Мотивация учебной деятельности учащихся.
Новые знания нам будет очень трудно осваивать без умения быстро и верно считать, поэтому, как всегда, начнем урок с устного счета:
1. Продолжите предложения:
- коэффициентом называется….
- подобные слагаемые – это слагаемые, у которых …
- привести подобные слагаемые – это выполнить действия с коэффициентами ….
- чтобы число умножить на сумму (разность), нужно …
- если перед скобкой стоит знак минус, то ….
- если перед скобкой стоит знак плюс, то …
2. Раскройте скобки:
-2(х – 5+а); 8(у+3-с); х ( - у+7 – с); -12(-2a+5b-4c+3d); (-3a-2b+5c+4d) ∙ (-15)
3. Актуализация знаний. Постановка цели и задач урока.
Задачи: организовать самостоятельное формулирование вопросов и постановку цели и задач урока; организовать самостоятельное планирование и выбор методов поиска информации.
На слайде представлена таблица. На столе у обучающихся карточки с примерами и ответы. Я предлагаю вам разгадать тему урока. Выполните вычисления в тетради, и в таблице напишите букву, соответствующую правильному ответу. Получившиеся слово – это тема урока. Я думаю, что вы справитесь с этим заданием за 4 минуты.
|
|
|
|
|
|
|
|
|
|
| 72 | -14 | -8 | -3,2 | -6 | 6 | -6 | -5,8 | 6 |
Раздаточный материал
| - 7,3 – 0,7 | 6 (Е) |
| -2,6 : (-0,4) | -8 (А) |
| -8*(-9) | -6 (Н) |
| 0,1 * (-32) | 72(У) |
| -19+5 | -5,8 (И) |
| 11,2-17 | -14 (Р) |
| -0,6 * 10 | -3,2 (В) |
Ребята по завершении времени называют буквы, соответствующие числам в таблице.
Верно, мы получили слово «уравнение». Запишите в тетрадях тему урока: «Уравнения».
Обратите внимание на записи.
b – 48:8 ; y ∙ 10=1800; 600 +1800: х ; 600 ∙ х=1800:3; a ∙ (56 - 40); у∙ 100 =600∙ 3;
k: (180:90) ; 600 ∙ х=1800; 5(х-3)= 20; х+8= -15; 6х=3х+9.
- Внимательно их изучите и ответьте на вопросы.
- На какие две группы можно разделить написанное?
- Как можно назвать каждую из групп?
- Интересна ли для нас 1 группа: выражения?
- А вторая? Почему?
– Какая тема сегодняшнего урока?
- Исходя из названия темы, давайте сформулируем цель нашего урока.
- Для того чтобы достичь цели урока, какие задачи нам надо поставить?
- Где можно узнать информацию по данной теме?
1) С уравнениями вы знакомы с начальной школы. Давайте вспомним: (1 мин)
- что такое уравнение;
- что значит решить уравнение;
- что такое корень уравнения?
2) Историческая справка: (2 мин)
Первым руководством по решению задач с неизвестным, получившим широкую известность, стал труд багдадского ученого IX в. Мухаммеда Бен Мусы аль-Хорезми. Слово "аль-джебр" из арабского названия этого трактата - "Китаб аль-джебр Валь-мукабала" (" Книга о восстановлении и противопоставлении") - со временем превратилось знакомое всем слово "алгебра". А само сочинение аль-Хорезми послужило отправной точкой в становлении науки о решении уравнений.
В сочинении аль-Хорезми неизвестные величины, так же как и все сопутствующие выкладки и преобразования уравнений, выражались словесно.
Такой стиль изложения, характерный для раннего этапа развития алгебры, историки науки называют риторическим (красноречивым).
Новый великий прорыв в алгебре связан с именем французского ученого XVI в. Франсуа Виета. Он первым из математиков ввел буквенные обозначения для коэффициентов уравнения и неизвестных величин. А традицией обозначать неизвестные величины последними буквами латинского алфавита (х, y или z) мы обязаны соотечественнику Виета - Рене Декарту.
3) Внимание (2 мин)
Перед вами уравнения. Выпишите в тетрадь те уравнения, которые вы не знаете, как решить. Что, именно, в выписанных уравнениях, вызывает у вас затруднение? Как решить остальные уравнения?
Обучающиеся выписывают уравнения №№2, 3, 5
| 1) | 2х + 3х = 15 |
| 2) | 8(х-2) = 40 |
| 3) | 5х =2х +6 |
| 4) | 3,2х = 0,64 |
| 5) | 2(2 – 3х) + 4 = 18 – (3 + х) |
| 6) | х :3 = – 9 |
4. Изучение нового материала.
Задача: организовать осмысленное восприятие новой информации.
1.Подготовительный этап.
– А что значит «решить уравнение»?
– Итак, уравнение – это равенство. А в жизни мы встречаемся с понятием равенство?
Актуализация и постановка проблемы.
– Давайте разберем такой пример. Весы находятся в равновесии. Что произойдет, если с одной чаши весов убрать груз?
– А что надо сделать, чтобы весы снова оказались в равновесии?
– Это свойство «весов» нам еще пригодится.
- Давайте вернемся к началу нашего урока. В тетрадях запишем уравнение и решим его. Какие существуют способы решения данного уравнения? [2]
- Хорошо! Давайте сначала решим уравнение, применив распределительное свойство умножения:
1 способ
8(x-2) = 40
8x-16=40
8x=40+16
8x=56
x=56:8
x=7
- А сейчас по правилу отыскания неизвестных компонентов
2 способ
8(x-2) = 40
- Что неизвестно в уравнении?
- Как найти неизвестный множитель?
x-2=40:8
x-2=5
x=5+2
x=7
-Что мы получили в итоге?
- Что называется корнем уравнения?
-Число 7 является корнем уравнения x-2=5 и уравнения8(x-2) = 40, так как 7-2=5 и
8(7-2)=40.
- Как из первого уравнения можно получить второе?
Мы с вами убедились, что корнем этих двух уравнений является одно и то же число. Поэтому:
Корни уравнения не изменяются, если обе части уравнения умножить или разделить на одно и тоже число, не равное нулю.
2. Снова вернемся к началу урока и теперь рассмотрим второе уравнение: x+8= - 15.
Как его можно решить?
Это уравнение решается с использованием зависимостей между компонентами и результатами математических действий. Но изучение отрицательных чисел дает возможность решить эти уравнения иначе.
- Вспомним, чему равна сумма противоположных чисел?
- Как можно получить в левой части уравнения только переменную x?
- Рассмотрим решение этих уравнений.
x+8= - 15
x+8-8= -15-8
x=-23
- Мы видим, что слагаемые без переменной перешли из левой части уравнения в правую с противоположным знаком.
- А сейчас рассмотрим третье уравнение и решим его: 5х=2х+6
- Чем данное уравнение отличается от предыдущего?
- Как его можно решить?
- Нужно получить такое уравнение, чтобы слагаемые с x были только слева. Что для этого необходимо сделать? (№3)
5х=2х+6
5x+ (-2x) = 2х+6+ (-2x)
5x+ (-2x) = 6
3x=6
x=6:3
x=2
- Хорошо! Давайте рассмотрим такой вопрос: Вы собираетесь за границу. О чем в первую очередь вы должны подумать, когда пересечете границу?
- Правильно, пересекая границу, вам обязательно надо поменять паспорт.
- Давайте представим, что знак «=» - это граница, а знак числа – это ваш паспорт. Когда мы пересекаем границу, меняем паспорт, то есть, если число переносим из одной части в другую, мы должны поменять знак.
Корни уравнения не изменяются, если какое – нибудь слагаемое перенести из одной части уравнения в другую, изменив при этом его знак.
-Хорошо, а уравнение под №5 решим на следующем уроке
5. Первичное осмысление и закрепление знаний.
Задачи: обеспечить осмысленное усвоение и закрепление знаний; выявление пробелов первичного осмысления изученного материала, коррекция выявленных пробелов, обеспечение закрепления в памяти детей знаний и способов действий, которые им необходимы для самостоятельной работы по новому материалу.
Принято при решении уравнений переносить слагаемые так, чтобы в левой части уравнения были неизвестные числа, а в правой - известные числа.
№1314 Перенесите из левой части уравнения в правую то слагаемое, которое не содержит неизвестного: а) 8х+ 5,9=7х+20; б) 6х-8= -5х -1,6.
и №1315 Соберите в левой части уравнения все слагаемые, содержащие неизвестное, а в правой – не содержащие неизвестное: а) 15y -8= - 6y +4,6;б) -16z+1,7 =2z -1 с комментированием на месте.
№1316 а) 6х-12=5х+4; б) -9а+8= -10а-2; (работа в парах).
№1318 а) -40(-7х+5)= -1600
6. Физкультминутка.
Дружно с вами мы решали и про числа рассуждали,
А теперь мы дружно встали, свои косточки размяли.
На счет раз кулак сожмем, на счет два в локтях сожмем.
На счет три — прижмем к плечам, на 4 — к небесам
Хорошо прогнулись, и друг другу улыбнулись
Про пятерку не забудем — добрыми всегда мы будем.
На счет шесть прошу всех сесть.
Числа, я и вы, друзья, вместе дружная семья.
7. Самостоятельная работа с самопроверкой по эталону.
Задачи: организовать выполнение учащимися самостоятельной работы на новое знание;
- организовать самопроверку по эталону;
- организовать выявление места и причины затруднений, работу над ошибками.
Вариант 1.
1.Решите уравнения:
а) 9х = -36;
б) 18х – 21 = 6 + 9х;
в) 7 – 4х = 14х + 7;
г)19х – 13= 23х - 21;
Вариант 2.
1.Решите уравнения:
а) -8х = 48;
б) 16х – 24 = 9 + 5х;
в) 1 – 2х = 12х + 1;
г)24х – 18= 27х - 24;
- У кого всё правильно?
- У кого есть ошибки?
- В каком месте ошибки?
- В чём причина? - Исправьте ошибки.
Выполняют самопроверку по эталону. Фиксируют «!», «?». Оценивают свою работу (по 1 баллу за каждое уравнение).
4 балла - оценка «5»;
3 балла - оценка «4»;
2 балла - оценка «3»;
1-0 баллов - надо еще поработать.
8. Включение в систему знаний и повторение.
Задачи: закреплять умение решать уравнения, применяя свойства уравнений
№1340 Старинная задача на составление уравнение :
-Скажи мне, учитель, сколько учеников посещают твою школу и слушают твои беседы.
-Вот сколько,- ответил учитель. – Половина изучает математику, четверть – природу, седьмая часть проводит время в размышлении, и кроме того, есть ещё три женщины.
Решение: Пусть х человек все ученики, тогда 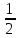 х –изучают математику,
х –изучают математику,  х –природу,
х –природу,  х-размышляют и + 3.
х-размышляют и + 3.
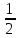 х +
х +  х +
х +  х + 3= х Ответ : 28 учеников.
х + 3= х Ответ : 28 учеников.
9. Информация о домашнем задании.
- На доске: Домашнее задание: п. 42, выучить правила; решить №1342(а; б; в; г) – на оценку «3», №1346 – на оценку «4», №1349– на оценку «5»- Ваши вопросы по домашнему заданию.
10. Рефлексия деятельности на уроке.
Задачи: зафиксировать новое содержание; осознание учащимися своей учебной деятельности, самооценка результатов деятельности своей и всего класса.
Что мы хотели узнать? Что мы узнали? На все ли вопросы мы получили ответы?
- Давайте еще раз вспомним определение уравнения, корня уравнения.
-Кто желает сформулировать правило решения уравнений нового вида?
-Что было самым сложным на уроке, а самым интересным?
-Кому не понадобится помощь при выполнении домашнего задания по этой теме?
Оценить отдельных учащихся
11. Домашнее задание. № 1341а-в; №1342а, в, е; 1344





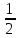 х –изучают математику,
х –изучают математику,  х –природу,
х –природу,  х-размышляют и + 3.
х-размышляют и + 3.









