| 3.Актуализация знаний, постановка проблемы и ее решение (20 мин) | В науке и практике часто встречаются задачи, решая которые приходится составлять различные комбинации из конечного числа элементов и подсчитывать число этих комбинаций. Вам в повседневной жизни часто приходится составлять различные комбинации. Например: в каком порядке можно сесть за парты на сегодняшнем занятии. А как же называется раздел математики, который занимается решением таких задач?
Сегодня основной целью нашего занятия будет: знакомство с понятиями «комбинаторика», размещения, перестановки и сочетания. А кто попробует своими словами дать определение понятию «комбинаторика»? Все верно. Слово «комбинаторика» произошло от латинского слова «combinare», что означает «соединять, сочетать». Отметим, что всякое случайное событие является следствием очень многих причин. Например, выпадение орла или решки при бросании монеты зависит от силы, с которой брошена монета, ее формы, сплава и многих других причин. Попадание или промах при стрельбе зависят от расстояния до мишени, формы и веса пули (снаряда), от направления и силы ветра и других случайных причин. В связи с этим невозможно заранее предсказать, произойдет единичное событие или нет. Иначе обстоит дело при изучении многократно повторяющихся опытов. Однородные случайные события при многократном повторении опыта подчиняются определенным закономерностям. Изучением этих закономерностей и занимается теория вероятностей. Каждый день вы встречаетесь с перебором различных вариантов. Задача 1. Давайте рассмотрим задачу из жизни. Если из города А в город В можно добраться тремя способами, а из города В в С – двумя способами, то из города А в город С можно добраться 2*3=6 способами. Как же это получается. Давайте разберем в виде схемы.
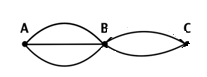
Из А в С можно добраться 2*3=6 способами. Данная задача приводит нас к основному правилу комбинаторики. Основное правило комбинаторики: пусть требуется выполнить одно за другим 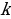 действий. Если первое действие можно выполнить действий. Если первое действие можно выполнить 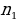 способами, второе способами, второе 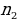 способами, третье - способами, третье - 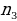 способами и т.д., то все способами и т.д., то все 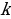 действий могут быть выполнены действий могут быть выполнены 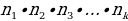 способами. способами. В нашей задаче из А в В можно добраться 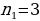 способами, из В в С можно добраться способами, из В в С можно добраться 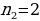 способами. Следовательно, из А в С можно добраться способами. Следовательно, из А в С можно добраться 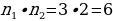 способами способами В комбинаторике есть три основные задачи: размещения, перестановки, сочетания.
Задача 2. В группе 20 обучающихся. Сколькими способами могут быть выбраны староста и заместитель старосты? Решение. Пусть сначала избирается староста. Поскольку каждый член группы может быть выбран старостой, то, очевидно, есть 20 способов его выбора. Тогда заместителем старосты может стать каждый из оставшихся 19 человек. На первом этапе мы используем 20 способов выбора старосты 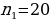 , на втором – 19 способов выбора заместителя старосты , на втором – 19 способов выбора заместителя старосты 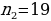 . В итоге, чтобы выбрать старосту и заместителя старосты применяем основное правило комбинаторики . В итоге, чтобы выбрать старосту и заместителя старосты применяем основное правило комбинаторики 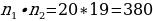 способов. способов. А теперь давайте немного порассуждаем. В качестве первого элемента может быть выбран любой из данных 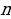 элементов, то первый элемент можно выбрать элементов, то первый элемент можно выбрать 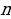 различными способами. Очевидно, что в качестве второго элемента можно выбрать любой из оставшихся различными способами. Очевидно, что в качестве второго элемента можно выбрать любой из оставшихся 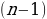 элементов, поэтому его можно выбрать элементов, поэтому его можно выбрать 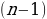 различными способами. Так как каждый из способов выбора первого элемента можно объединить с каждым из способов выбора второго элемента, то существуют различными способами. Так как каждый из способов выбора первого элемента можно объединить с каждым из способов выбора второго элемента, то существуют 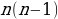 различных способов выбора первых двух элементов. А вот если таких элементов будет не два как в нашем случае, а различных способов выбора первых двух элементов. А вот если таких элементов будет не два как в нашем случае, а 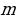 элементов, то основная формула комбинаторики будет выглядить так: элементов, то основная формула комбинаторики будет выглядить так: 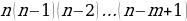 выбора выбора 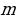 различных элементов. различных элементов. Такую формулу в комбинаторике назвали числом всех возможных размещений из 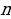 элементов по элементов по 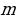 элементов и обозначают элементов и обозначают 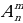 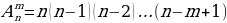 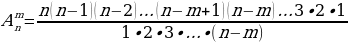 Факториал натурального числа n определяется как произведение всех натуральных чисел от 1 до n включительно: 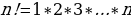 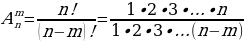 – формула числа размещений – формула числа размещений Определение: Размещениями из 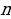 элементов по элементов по 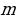 элементов называется упорядоченное подмножество, содержащее элементов называется упорядоченное подмножество, содержащее 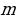 различных элементов данного множества. различных элементов данного множества. Решим нашу предыдущую задачу используя формулу числа размещений. Число всех возможных размещений 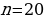 . А нам необходимо выбирать только по два, следовательно . А нам необходимо выбирать только по два, следовательно 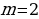 . . 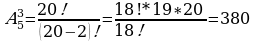 Задача 3. 10 молодых людей решили отпраздновать окончание института товарищеским обедом в ресторане. Когда все собрались, и первое блюдо было подано, заспорили о том, как усесться вокруг стола. Одни предлагали разместиться в алфавитном порядке, другие - по возрасту, третьи - по успеваемости, четвертые - по росту и т.д. Спор затянулся, суп успел остыть, а за стол никто не садился. Примирил всех официант, обратившийся к ним с такой речью: - Друзья мои, оставьте ваши пререкания. Сядьте за стол как придется и выслушайте меня. Как вы думаете какой способ предложил официант, чтобы прекратить данный спор. Теперь я вам зачитаю предложение официанта. Все сели как попало. Официант продолжал: пусть один из вас запишет, в каком порядке вы сейчас сидите. Завтра вы снова явитесь сюда пообедать, и разместитесь уже в ином порядке. Послезавтра сядете опять по-новому и т.д., пока не перепробуете все возможные размещения. Когда же придет черед вновь сесть так, как сидите вы здесь сегодня, тогда я начну ежедневно угощать вас бесплатно самыми изысканными обедами. Предложение понравилось. Решено было ежедневно собираться в этом ресторане и перепробовать все способы размещения за столом, чтобы скорее начать пользоваться бесплатными обедами. Однако дождаться этого дня им не пришлось. И не потому, что официант не исполнил обещания, а потому, что число всех возможных размещений за столом чересчур велико. Оно равняется, - ни мало, ни много, - 3 628 800. (Чуть позже поймем, как получили данное число). Такое число дней составляет почти 10 тысяч лет! Это, на первый взгляд, невероятно, но так оно и есть! Этот метод тоже можем отнести к методу «размещения», разница только в том, что 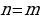 . Поэтому этому методу дали другое название «перестановки». . Поэтому этому методу дали другое название «перестановки». Определение: Перестановкой из 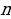 элементов называется размещение из элементов называется размещение из 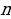 . элементов по . элементов по 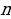 . элементов. . элементов. 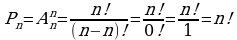 Применяем формулу и получаем 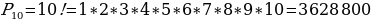 Следующую задачу решим у доски. Задача №4. В группе из 20 обучающихся нужно выделить четырех для работы на определенном участке. Сколькими способами это можно сделать? Для решения данной задачи я хочу вас познакомить с еще одним методом, который называется «сочетания». Определение: Сочетанием из 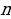 элементов по элементов по 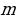 элементов называется любое подмножество, которое содержит элементов называется любое подмножество, которое содержит 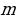 различных элементов данного множества. различных элементов данного множества. Следовательно, сочетания из n элементов по m элементов – это все m-элементные подмножества n-элементного множества, причем различными подмножествами считаются только те, которые имеют неодинаковый состав элементов. Число всех возможных сочетаний из 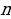 элементов по элементов по 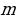 элементов обозначают элементов обозначают 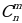 , где , где 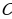 - первая буква французского слова combination– сочетание. - первая буква французского слова combination– сочетание. Число 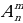 размещений из размещений из 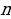 элементов по элементов по 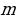 найдем следующим образом. Сначала составим все возможные подмножества, содержащие по найдем следующим образом. Сначала составим все возможные подмножества, содержащие по 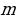 различных элементов. Их число равно различных элементов. Их число равно 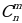 . Затем в каждом из полученных таким образом подмножеств (сочетаний) сделаем перестановки, в результате получим все размещения из . Затем в каждом из полученных таким образом подмножеств (сочетаний) сделаем перестановки, в результате получим все размещения из 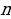 элементов по элементов по 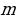 . Так как число перестановок из . Так как число перестановок из 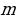 элементов равно элементов равно 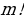 , то число , то число 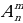 размещений из размещений из 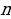 элементов по элементов по 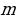 будет в будет в 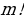 раз больше, чем число раз больше, чем число 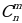 сочетаний из сочетаний из 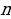 элементов по элементов по 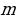 , т.е. , т.е. 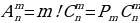 Отсюда получаем Формула: 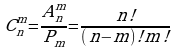 Теперь возвращаемся к решению задачи. 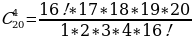 =4845 =4845 Вот мы и разобрали возможные варианты решения задач. Теперь пора сделать вывод: если порядок расположения элементов в выбираемых соединениях не важен, то для определения количества таких соединений используют формулу числа сочетаний 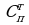 . Приведите пример: . Приведите пример: Если при выборе тех же студентов каждому из них выдаются разные задания, то порядок их выбора влияет на номер полученного задания, что является существенным.
Какую формулу применить? Молодцы. А теперь давайте проверим знания, полученные на данном занятии. |
Отвечают на вопрос: Данная наука называется комбинаторика. Записывают в тетрадь тему урока: «Размещения, перестановки и сочетания» Ответы учащихся: «комбинаторика», значит комбинировать, сочетать
Записывают в тетрадь: Основное правило комбинаторики: пусть требуется выполнить одно за другим 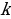 действий. Если первое действие можно выполнить действий. Если первое действие можно выполнить 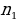 способами, второе способами, второе 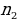 способами, третье - способами, третье - 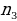 способами и т.д., то все способами и т.д., то все 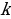 действий могут быть выполнены действий могут быть выполнены 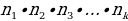 способами. способами. Задача 1. 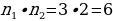 способов способов
Задача 2. 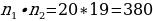 способов. способов.
Записывают в тетрадь: 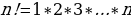
Размещениями из 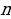 элементов по элементов по 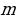 элементов называется упорядоченное подмножество, содержащее элементов называется упорядоченное подмножество, содержащее 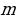 различных элементов данного множества. различных элементов данного множества. 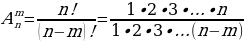 – формула числа размещений – формула числа размещений
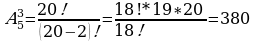
Обучающиеся предлагают различные свои варианты.
Перестановкой из 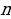 элементов называется размещение из элементов называется размещение из 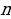 . элементов по . элементов по 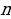 . элементов. . элементов. 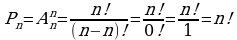 Задача 3: Задача 3: 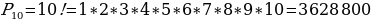
Сочетанием из 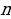 элементов по элементов по 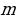 элементов называется любое подмножество, которое содержит элементов называется любое подмножество, которое содержит 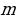 различных элементов данного множества. различных элементов данного множества.
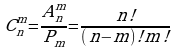 Задача 4: 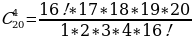 =4845 =4845
Ответы обучающихся: выбор 4 обучающихся из группы в 20 студентов для выполнения одинаковой работы.
В этом случае следует использовать формулу числа размещений 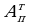 . . | Личностные: осознание своих возможностей; отвечая на поставленные вопросы по вероятности и комбинаторики, анализируя и сравнивая, находят необходимую информацию для решения задач. Регулятивные: целеполагание, прогнозирование |
| 4.Закрепление изученного материала (13 мин)
| Определите какую формулу необходимо применить: размещения, сочетания или перестановки. Задача №5 (решаем у доски) Сколькими способами могут быть присуждены первая, вторая и третья премии трём лицам из 10 соревнующихся?
Задача №6 (решаем у доски) Сколькими способами можно расставить на одной полке шесть различных книг?
Задача №7 Сколько матчей будет сыграно в футбольном чемпионате с участием 16 команд, если каждые две команды встречаются между собой один раз? 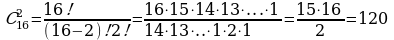 Ответ: 120 матчей (сочетания) А теперь давайте проверим свой знания математическим диктантом. На экране появятся задачи, вы должны на листочках написать какую формулу вы будете применять к каждой из заданных задач. Задача №8 Сколькими различными способами могут сесть на скамейку а) 5 человек; б) 7 человек.
Задача №9 Учащиеся должны посетить во вторник по расписанию 5 уроков по следующим предметам: литература, алгебра, география, физкультура и биология. Сколькими способами можно составить расписание на этот день, чтобы физкультура была пятым уроком? Задача №10 На станции имеется 8 запасных путей. Сколькими способами можно расставить на них четыре поезда.
Задача №11 Учащиеся школы изучают 12 различных предметов. Сколькими способами можно составить расписание уроков на один день, чтобы в нём было 5 различных предметов?
| Обучающиеся решают комбинаторные задачи Обучающийся у доски: Задача 5: 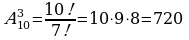 . . Ответ: 720 способов. (размещения) Задача 6: Решение: Искомое число способов равно числу перестановок из 6 элементов, .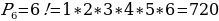 Ответ: 720 (перестановки) Задача 7: Учащиеся решают задачу самостоятельно
Решают индивидуальные задания, применяют таблицу 2 «Факториалы от 0 до 10», стр.53 Задача 8: Решение: а) Р5 = 5! = 120; б) Р7 = 7! = 5 040. Ответ: а) 120 способов; б) 5 040 способов. (перестановки)
Задача 9: Решение: Р4 = 4! = 24. Ответ: 24 способа. (перестановки)
Задача 10: Решение: 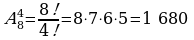 . . Ответ: 1 680 способов. (размещения) Задача 11: Решение: 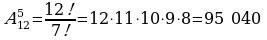 Ответ: 95 040 способов. Ответ: 95 040 способов. Результаты оценки собственных знаний заносят в оценочные листы. | Личностные: осознание своих возможностей, самоорганизация развитие логического мышления.
|








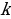 действий. Если первое действие можно выполнить
действий. Если первое действие можно выполнить 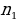 способами, второе
способами, второе 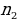 способами, третье -
способами, третье - 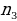 способами и т.д., то все
способами и т.д., то все 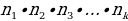 способами.
способами. 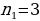 способами, из В в С можно добраться
способами, из В в С можно добраться 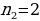 способами. Следовательно, из А в С можно добраться
способами. Следовательно, из А в С можно добраться 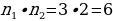 способами
способами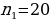 , на втором – 19 способов выбора заместителя старосты
, на втором – 19 способов выбора заместителя старосты 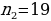 . В итоге, чтобы выбрать старосту и заместителя старосты применяем основное правило комбинаторики
. В итоге, чтобы выбрать старосту и заместителя старосты применяем основное правило комбинаторики 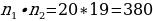 способов.
способов.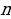 элементов, то первый элемент можно выбрать
элементов, то первый элемент можно выбрать 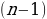 элементов, поэтому его можно выбрать
элементов, поэтому его можно выбрать 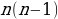 различных способов выбора первых двух элементов. А вот если таких элементов будет не два как в нашем случае, а
различных способов выбора первых двух элементов. А вот если таких элементов будет не два как в нашем случае, а 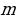 элементов, то основная формула комбинаторики будет выглядить так:
элементов, то основная формула комбинаторики будет выглядить так: 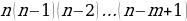 выбора
выбора 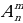
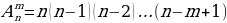
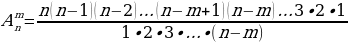
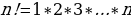
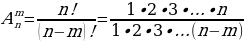 – формула числа размещений
– формула числа размещений 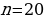 . А нам необходимо выбирать только по два, следовательно
. А нам необходимо выбирать только по два, следовательно 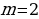 .
.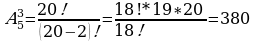
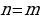 . Поэтому этому методу дали другое название «перестановки».
. Поэтому этому методу дали другое название «перестановки».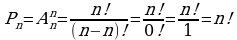
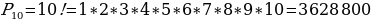
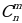 , где
, где 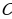 - первая буква французского слова combination– сочетание.
- первая буква французского слова combination– сочетание.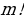 , то число
, то число 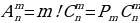
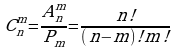
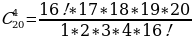 =4845
=4845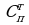 . Приведите пример:
. Приведите пример: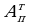 .
.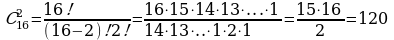
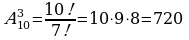 .
. 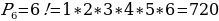
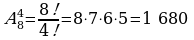 .
.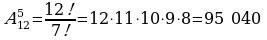 Ответ: 95 040 способов.
Ответ: 95 040 способов.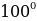 при нормальном атмосферном давлении, то обязательно наступит процесс кипения воды.
при нормальном атмосферном давлении, то обязательно наступит процесс кипения воды.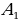 – «появилась стандартная деталь» и
– «появилась стандартная деталь» и 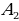 – «появилась нестандартная деталь» являются несовместными событиями. Пример 2. Брошена игральная кость. Событие
– «появилась нестандартная деталь» являются несовместными событиями. Пример 2. Брошена игральная кость. Событие 









