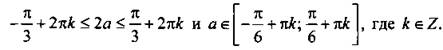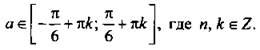План урока
Предмет: алгебра
Преподаватель: Амирханова А. К.
Дата проведения:____________
Тема урока: Зачетная работа по теме «Преобразование тригонометрических выражений»
Цель: проверить знания учащихся по вариантам одинаковой сложности.
Ход уроков
I. Сообщение темы и цели уроков
II. Характеристика зачетной работы
III. Варианты зачетной работы
Вариант 1
А
1. Дано:  Найдите sin a, tg a, ctg a.
Найдите sin a, tg a, ctg a.
2. Сравните числа cos14°cos74° и ½.
3. Вычислите 
4. Постройте график функции 
5. Решите уравнение 
6. Решите неравенство 
7. Упростите выражение 
В
8. Дано:  Найдите cos a - sin a.
Найдите cos a - sin a.
9. Сравните числа 
10. Найдите область значений функции 
11. Упростите выражение 
12. Найдите значение выражения  если
если 
13. Найдите множество значений функции 
14. Решите уравнение 
Вариант 2
А
1. Дано:  Найдите sin a, tg a, ctg a.
Найдите sin a, tg a, ctg a.
2. Сравните числа 
3. Вычислите 
4. Постройте график функции 
5. Решите уравнение 
6. Решите неравенство 
7. Упростите выражение 
В
8. Дано:  Найдите cos а - sin а.
Найдите cos а - sin а.
9. Сравните числа 
10. Найдите область значений функции у = 12 sin x + 5 cos x - 4.
11. Упростите выражение 
C
12. Найдите значение выражения  если
если 
13. Найдите множество значений функции 
14. Решите уравнение 
IV. Ответы и решения
Вариант 1

2. Второе число больше.

4. График у = 2|cos х|.

9. Первое число больше.
10. Е(у) = [-10; 16].
11. -1.
12. В подкоренных выражениях умножим числители и знаменатели дробей на сопряженную величину знаменателя. Получим

В силу ограниченности функции sin а при всех а величины  Так как
Так как  то cos a < 0 и |cos a| = -cos a. Поэтому выражение
то cos a < 0 и |cos a| = -cos a. Поэтому выражение  Для значения tg a = -1/3 найдем значение данного выражения:
Для значения tg a = -1/3 найдем значение данного выражения: 
Ответ: 2/3.
13. Используем метод введения вспомогательного угла и преобразуем функцию: 
 Учтем, что функция арксинуса возрастающая, и запишем неравенства
Учтем, что функция арксинуса возрастающая, и запишем неравенства 
 тогда -6 ≤ y ≤ 2. Таким образом, множество значений данной функции Е(у) = [-6; 2].
тогда -6 ≤ y ≤ 2. Таким образом, множество значений данной функции Е(у) = [-6; 2].
Ответ: [-6; 2].
14. Преобразуем сумму двух последних функций в произведение: sin x + 2 sin a cos х = 2. Используем метод введения вспомогательного угла. Разделим все члены уравнения на  Получаем:
Получаем:  Будем считать, что
Будем считать, что  тогда tgφ = 2 sin a и φ = arctg(2 sin a). Уравнение имеет вид:
тогда tgφ = 2 sin a и φ = arctg(2 sin a). Уравнение имеет вид:  решения которого
решения которого  и
и  При этом должно выполняться неравенство
При этом должно выполняться неравенство  Решим его и получим:
Решим его и получим:  или
или  илиcos 2a ≤ -1/2, откуда
илиcos 2a ≤ -1/2, откуда 
Ответ:  при
при 
Вариант 2

2. Второе число больше.

4. График у = 2|sin2x|.


9. Второе число больше.
10. Е(у) = [-9; 17].
11. 1.
12. В подкоренных выражениях умножим числители и знаменатели дробей на сопряженную величину знаменателя. Получим:

В силу ограниченности функции sin а при всех а величины  Так как
Так как  то cos a > 0 и |cos a| = cos a. Поэтому выражение
то cos a > 0 и |cos a| = cos a. Поэтому выражение  Для значения tg a = -1/2 найдем значение данного выражения: 2 · (-1/2) = -1.
Для значения tg a = -1/2 найдем значение данного выражения: 2 · (-1/2) = -1.
Ответ: -1.
13. Используем метод введения вспомогательного угла и преобразуем функцию: 
 Учтем, что функция арккосинуса убывающая, и запишем неравенства
Учтем, что функция арккосинуса убывающая, и запишем неравенства 
 тогда 3 ≥ у ≥ 0. Таким образом, множество значений данной функции Е(у) = [0; 3].
тогда 3 ≥ у ≥ 0. Таким образом, множество значений данной функции Е(у) = [0; 3].
Ответ: [0; 3].
14. Преобразуем сумму двух последних функций в произведение: sin х + 2 cos a cos x= 2. Используем метод введения вспомогательного угла. Разделим все члены уравнения на  Получим:
Получим:  Будем считать, что
Будем считать, что  тогда tg φ = 2 cos a и φ = arctg(2 cos a). Уравнение имеет вид:
тогда tg φ = 2 cos a и φ = arctg(2 cos a). Уравнение имеет вид:  решения которого
решения которого  и
и  При этом должно выполняться неравенство
При этом должно выполняться неравенство  Решим его и получим:
Решим его и получим:  или
или  или
или  откуда
откуда 
Ответ:  при
при 
Просмотр содержимого документа
«Тема урока: Зачетная работа по теме «Преобразование тригонометрических выражений»»
План урока
Предмет: алгебра
Преподаватель: Амирханова А. К.
Дата проведения:____________
Тема урока: Зачетная работа по теме «Преобразование тригонометрических выражений»
Цель: проверить знания учащихся по вариантам одинаковой сложности.
Ход уроков
I. Сообщение темы и цели уроков
II. Характеристика зачетной работы
III. Варианты зачетной работы
Вариант 1
А
1. Дано: 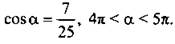 Найдите sin a, tg a, ctg a.
Найдите sin a, tg a, ctg a.
2. Сравните числа cos14°cos74° и ½.
3. Вычислите 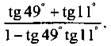
4. Постройте график функции 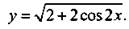
5. Решите уравнение 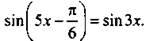
6. Решите неравенство 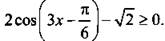
7. Упростите выражение 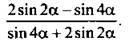
В
8. Дано: 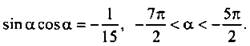 Найдите cos a - sin a.
Найдите cos a - sin a.
9. Сравните числа 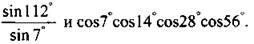
10. Найдите область значений функции 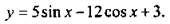
11. Упростите выражение 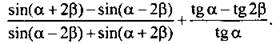
12. Найдите значение выражения 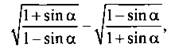 если
если 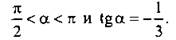
13. Найдите множество значений функции 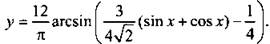
14. Решите уравнение 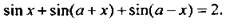
Вариант 2
А
1. Дано: 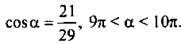 Найдите sin a, tg a, ctg a.
Найдите sin a, tg a, ctg a.
2. Сравните числа 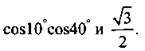
3. Вычислите 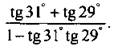
4. Постройте график функции 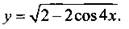
5. Решите уравнение 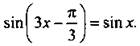
6. Решите неравенство 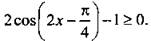
7. Упростите выражение 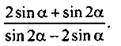
В
8. Дано: 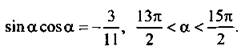 Найдите cos а - sin а.
Найдите cos а - sin а.
9. Сравните числа 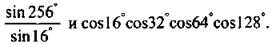
10. Найдите область значений функции у = 12 sin x + 5 cos x - 4.
11. Упростите выражение 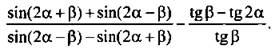
C
12. Найдите значение выражения 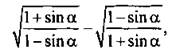 если
если 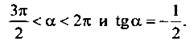
13. Найдите множество значений функции 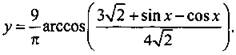
14. Решите уравнение 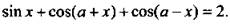
IV. Ответы и решения
Вариант 1
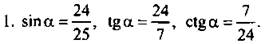
2. Второе число больше.
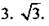
4. График у = 2|cos х|.
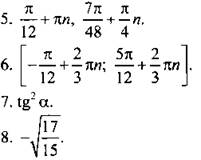
9. Первое число больше.
10. Е(у) = [-10; 16].
11. -1.
12. В подкоренных выражениях умножим числители и знаменатели дробей на сопряженную величину знаменателя. Получим
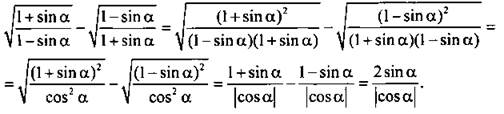
В силу ограниченности функции sin а при всех а величины 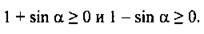 Так как
Так как 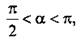 то cos a cos a| = -cos a. Поэтому выражение
то cos a cos a| = -cos a. Поэтому выражение 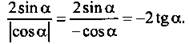 Для значения tg a = -1/3 найдем значение данного выражения:
Для значения tg a = -1/3 найдем значение данного выражения: 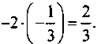
Ответ: 2/3.
13. Используем метод введения вспомогательного угла и преобразуем функцию: 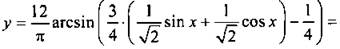
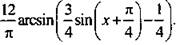 Учтем, что функция арксинуса возрастающая, и запишем неравенства
Учтем, что функция арксинуса возрастающая, и запишем неравенства 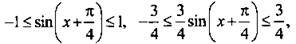
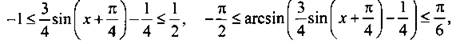 тогда -6 ≤ y ≤ 2. Таким образом, множество значений данной функции Е(у) = [-6; 2].
тогда -6 ≤ y ≤ 2. Таким образом, множество значений данной функции Е(у) = [-6; 2].
Ответ: [-6; 2].
14. Преобразуем сумму двух последних функций в произведение: sin x + 2 sin a cos х = 2. Используем метод введения вспомогательного угла. Разделим все члены уравнения на 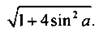 Получаем:
Получаем: 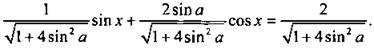 Будем считать, что
Будем считать, что 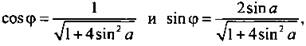 тогда tgφ = 2 sin a и φ = arctg(2 sin a). Уравнение имеет вид:
тогда tgφ = 2 sin a и φ = arctg(2 sin a). Уравнение имеет вид: 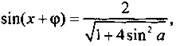 решения которого
решения которого 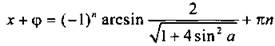 и
и 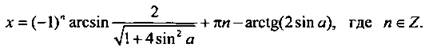 При этом должно выполняться неравенство
При этом должно выполняться неравенство 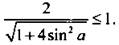 Решим его и получим:
Решим его и получим: 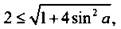 или
или 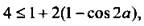 илиcos 2a ≤ -1/2, откуда
илиcos 2a ≤ -1/2, откуда 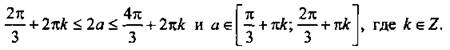
Ответ: 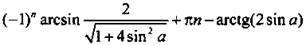 при
при 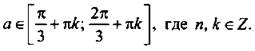
Вариант 2
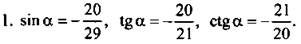
2. Второе число больше.
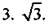
4. График у = 2|sin2x|.
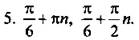
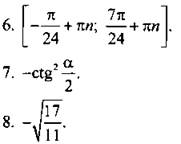
9. Второе число больше.
10. Е(у) = [-9; 17].
11. 1.
12. В подкоренных выражениях умножим числители и знаменатели дробей на сопряженную величину знаменателя. Получим:
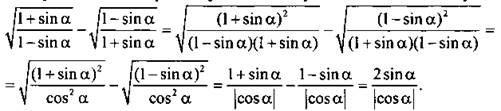
В силу ограниченности функции sin а при всех а величины 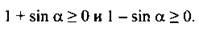 Так как
Так как 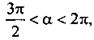 то cos a 0 и |cos a| = cos a. Поэтому выражение
то cos a 0 и |cos a| = cos a. Поэтому выражение 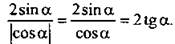 Для значения tg a = -1/2 найдем значение данного выражения: 2 · (-1/2) = -1.
Для значения tg a = -1/2 найдем значение данного выражения: 2 · (-1/2) = -1.
Ответ: -1.
13. Используем метод введения вспомогательного угла и преобразуем функцию: 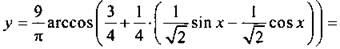
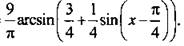 Учтем, что функция арккосинуса убывающая, и запишем неравенства
Учтем, что функция арккосинуса убывающая, и запишем неравенства 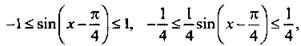
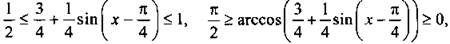 тогда 3 ≥ у ≥ 0. Таким образом, множество значений данной функции Е(у) = [0; 3].
тогда 3 ≥ у ≥ 0. Таким образом, множество значений данной функции Е(у) = [0; 3].
Ответ: [0; 3].
14. Преобразуем сумму двух последних функций в произведение: sin х + 2 cos a cos x= 2. Используем метод введения вспомогательного угла. Разделим все члены уравнения на 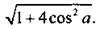 Получим:
Получим: 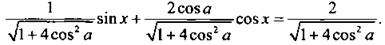 Будем считать, что
Будем считать, что 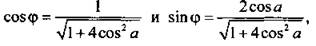 тогда tg φ = 2 cos a и φ = arctg(2 cos a). Уравнение имеет вид:
тогда tg φ = 2 cos a и φ = arctg(2 cos a). Уравнение имеет вид: 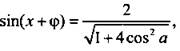 решения которого
решения которого 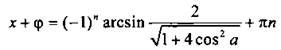 и
и 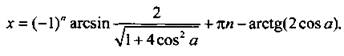 При этом должно выполняться неравенство
При этом должно выполняться неравенство 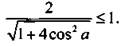 Решим его и получим:
Решим его и получим: 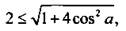 или
или 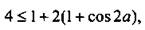 или
или 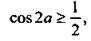 откуда
откуда 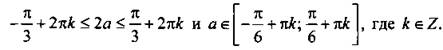
Ответ: 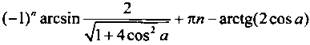 при
при 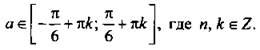






 Найдите sin a, tg a, ctg a.
Найдите sin a, tg a, ctg a.




 Найдите cos a - sin a.
Найдите cos a - sin a.


 если
если 


 Найдите sin a, tg a, ctg a.
Найдите sin a, tg a, ctg a.





 Найдите cos а - sin а.
Найдите cos а - sin а.

 если
если 






 Так как
Так как  то cos a < 0 и |cos a| = -cos a. Поэтому выражение
то cos a < 0 и |cos a| = -cos a. Поэтому выражение  Для значения tg a = -1/3 найдем значение данного выражения:
Для значения tg a = -1/3 найдем значение данного выражения: 

 Учтем, что функция арксинуса возрастающая, и запишем неравенства
Учтем, что функция арксинуса возрастающая, и запишем неравенства 
 тогда -6 ≤ y ≤ 2. Таким образом, множество значений данной функции Е(у) = [-6; 2].
тогда -6 ≤ y ≤ 2. Таким образом, множество значений данной функции Е(у) = [-6; 2]. Получаем:
Получаем:  Будем считать, что
Будем считать, что  тогда tgφ = 2 sin a и φ = arctg(2 sin a). Уравнение имеет вид:
тогда tgφ = 2 sin a и φ = arctg(2 sin a). Уравнение имеет вид:  решения которого
решения которого  и
и  При этом должно выполняться неравенство
При этом должно выполняться неравенство  Решим его и получим:
Решим его и получим:  или
или  илиcos 2a ≤ -1/2, откуда
илиcos 2a ≤ -1/2, откуда 
 при
при 





 Так как
Так как  то cos a > 0 и |cos a| = cos a. Поэтому выражение
то cos a > 0 и |cos a| = cos a. Поэтому выражение  Для значения tg a = -1/2 найдем значение данного выражения: 2 · (-1/2) = -1.
Для значения tg a = -1/2 найдем значение данного выражения: 2 · (-1/2) = -1.
 Учтем, что функция арккосинуса убывающая, и запишем неравенства
Учтем, что функция арккосинуса убывающая, и запишем неравенства 
 тогда 3 ≥ у ≥ 0. Таким образом, множество значений данной функции Е(у) = [0; 3].
тогда 3 ≥ у ≥ 0. Таким образом, множество значений данной функции Е(у) = [0; 3]. Получим:
Получим:  Будем считать, что
Будем считать, что  тогда tg φ = 2 cos a и φ = arctg(2 cos a). Уравнение имеет вид:
тогда tg φ = 2 cos a и φ = arctg(2 cos a). Уравнение имеет вид:  решения которого
решения которого  и
и  При этом должно выполняться неравенство
При этом должно выполняться неравенство  Решим его и получим:
Решим его и получим:  или
или  или
или  откуда
откуда 
 при
при 
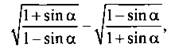 если
если 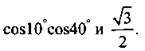
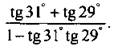
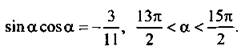 Найдите cos а - sin а.
Найдите cos а - sin а.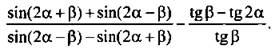
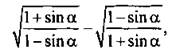 если
если 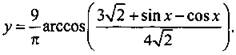
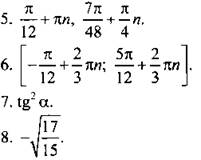
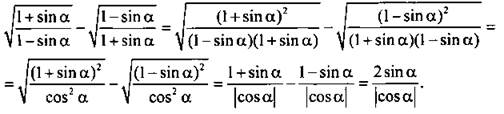
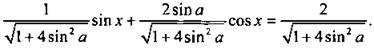 Будем считать, что
Будем считать, что 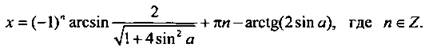 При этом должно выполняться неравенство
При этом должно выполняться неравенство 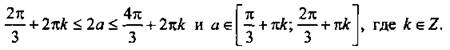
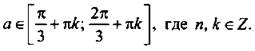
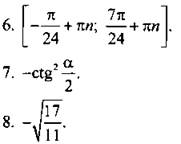
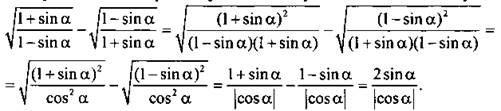
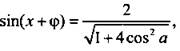 решения которого
решения которого 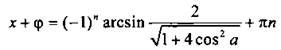 и
и 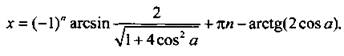 При этом должно выполняться неравенство
При этом должно выполняться неравенство