Теоремы в курсе планиметри. методика обучения доказательству теорем

_{ДЕПАРТАМЕНТ ОБРАЗОВАНИЯ И МОЛОДЕЖНОЙ ПОЛИТИКИ}

ХАНТЫ-МАНСИЙСКОГО АВТОНОМНОГО ОКРУГА – ЮГРЫ

БЮДЖЕТНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ

ХАНТЫ-МАНСИЙСКОГО АВТОНОМНОГО ОКРУГА-ЮГРЫ

«СУРГУТСКИЙ ГОСУДАРСТВЕННЫЙ ПЕДАГОГИЧЕСКИЙ УНИВЕРСИТЕТ»

Факультет управления

Кафедра высшей математики и информатики

ТЕОРЕМЫ В КУРСЕ ПЛАНИМЕТРИ. МЕТОДИКА ОБУЧЕНИЯ ДОКАЗАТЕЛЬСТВУ ТЕОРЕМ

Курсовая работа

Направление подготовки

44.03.05 Педагогическое образование

Направленность

Математика и Начальное образование

Уровень бакалавриата

Исполнитель: Онищенко Елизавета Александровна

обучающегося группы Б-7022

_____________

(подпись)

Научный руководитель: Суханова Н.В.,

кандидат педагогических наук, доцент

____________

(подпись)

Оценка: _________________

Заведующий кафедрой: Суханова Н.В.,

кандидат педагогических наук, доцент

_____________

(подпись)

Сургут

2021

Оглавление

Введение……………………………………………………………………	3
Глава 1. Теоретические основы методики обучения доказательству теорем планиметрии………………………………………………………..	5
1.1. Понятие теоремы и ее виды……………………………………	5
1.2 Методы доказательства математических теорем………………	12
Глава 2. Методические особенности доказательства теорем……………	20
2.1 Этапы работы с теоремами. Приемы мотивации изучения и доказательства теорем……………………………………………………...	20
2.2 Методика организации работы с теоремами при изучении курса планиметрии…………………………………………………………	30
Заключение………………………………………………………………….	36
Список использованной литературы……………………………………...	38
Приложение ………………………………………………………………...	43

 

Введение

Актуальностью исследования является то, что в настоящее время важнейшей задачей обучения на этапе основного общего образования является обеспечения результатов Федерального Государственного Образовательного Стандарта (далее ФГОС)[17]. Изучение предметной области "Математика и информатика" должно обеспечить комплекс задач, одной из которых является формирование представлений о математике как части общечеловеческой культуры, универсальном языке науки, позволяющем описывать и изучать реальные процессы и явления.

Безусловно, основными компонентами содержания математики являются понятия, задачи и теоремы. Задачи по арифметике и формулы связанные с геометрическими объектами уже встречались в египетских папирусах, написанных в III тысячелетии до н. э.. Однако в этих текстах не было самого главного — доказательств.

Методика преподавания математики всегда интересовали русских ученых – математиков и педагогов. Вопросом оказательства теорем занимались Е. Ф. Данилова, В. А. Далингер, Лященко, И. С. Градштейн и мн. другие.

В разработке методики преподавания математики участвует широкий круг ученых, методистов, учителей, которые печатают свои работы и делятся опытом на страницах журнала «Математика в школе», создают блоги в интернете и многое другое.

Обучение доказательству теорем нуждается в детальном рассмотрении. Известно, что учащиеся формально заучивают теорему и ее доказательство, не понимая его логического смысла [2]. Дополнительным вопросом учитель может выявить такое непонимание ученика, который как будто бы правильно доказал теорему. Формальное заучивание доказательства проявляется в затруднениях, которые испытывают школьники, если немного изменить, иначе расположить чертеж.

Формальное заучивание знаний, зубрежка, подкрепляемая бесконечным повторением, калечат мышление ученика. Как верно замечает Э. В. Ильенков[5], такое повторение «следовало бы назвать не матерью, а мачехой учения». Математического знания не существует, если учащийся просто запоминает материал, ибо работу мысли нельзя заменить работой памяти.

Чтобы учитель нас правильно понял, мы хотим подчеркнуть, что в обучении математике заучивание определений и формулировок теорем играет большую роль. А. Я. Хинчин [26] указывал на то, что «заучивание определений является актом высокой логической культуры, а не схоластической зубрежкой». Но такому заучиванию должна предшествовать работа, которая бы помогла школьнику осознать каждый элемент формулировки. Ученик иногда запоминает сочетания слов, которые от него часто требуют при обоснованиях, но при проверке можно обнаружить, что он говорит эти слова механически. Иногда, ученик, доказавший теорему, не может указать на чертеже те элементы, о которых он говорил при доказательстве [2].

Объект исследования: процесс обучения планиметрии.

Предмет исследования: методика обучения доказательству теорем.

Цель курсовой работы: раскрыть методические особенности обучения учащихся доказательству теорем при изучении планиметрии.

Задачи курсовой работы:

1. Раскрыть сущность понятия «теорема ее структуры и виды».

2. Выявить основные методы доказательства теорем.

3. Раскрыть особенности различных приемов работы с теоремами.

4. Разработать методические рекомендации, с некоторыми теоремами из курса планиметрии.

Работа состоит из 2 глав по 2 параграфа и заключения. Список использованных источников включает 38 наименований.

Глава 1. Теоретические основы методики обучения учащихся доказательству теорем

1. Понятие теоремы. Строение математических теорем

Формирование и использование умений рассуждать, проводить доказательства, аргументировать высказывания проводится во всех учебных предметах. Однако бесспорно, что развитию способностей школьников анализировать данные, принимать решения и обосновывать свой выбор в наибольшей мере способствует изучение математики.

А.В. Погорелов[19] цель преподавания геометрии в школе выразил так: «Главная задача преподавания геометрии в школе - научить учащихся логически рассуждать, аргументировать свои утверждения, доказывать. Очень немногие из окончивших школу будут математиками, тем более геометрами. Будут и такие, которые в их практической деятельности ни разу не воспользуются теоремой Пифагора. Однако вряд ли найдётся хотя бы один, которому не придётся рассуждать, анализировать, доказывать»

Для начала работы необходимо выяснить определить основные понятия, с которыми необходимо работать – это суждение, аксиома и теорема.

С.И. Ожегов в «Толковом словаре русского языка»[18] говорит, что «Суждение – форма мышления, представляющая собой сочетания понятий, из которых одно(субъект) определяется и раскрывается через другое (предикат)»

В большой Российской Энциклопедии [13] приводятся следующие определения суждение - (высказывание), логич. категория, обозначающая мысль, в которой утверждается или отрицается к.-л. положение дел в действительности (наличие или отсутствие связей между предметами и их свойствами или отношений между предметами), именно с данным понятием мы будем работать.

В зависимости от объёма и содержания отображаемых в суждении предметов и от характера связи предметов и свойств Н.И. Кондаков в «Логическом словаре-справочнике»[21]приводит следующие классификации суждений:

«Классификация суждений по Кондакову Н.И.»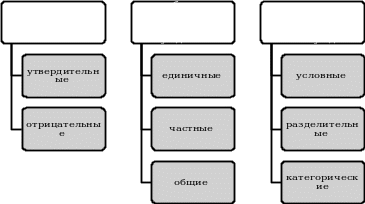

Рисунок 1

Принято выделять четыре основных вида суждений (табл.1):

Таблица 1

Виды суждений

Название суждения	Обозначение	Запись суждения на языке формальной логики	Запись суждения на языке логики предикатов
Общеутвердительное	A	Все S суть P	Каков бы ни был объект x, если он обладает свойством S, то обладает также свойством P
Частноутвердительное	I	Некоторые S суть P	Существует такой объект x, обладающий свойством S, который также обладает и свойством P.
Продолжение таблицы
Общеотрицательное	E	Никакое S не суть P (Все S суть не P)	Каков бы ни был объект x, если он обладает свойством S, то он не обладает свойством P
Частноотрицательное	O	Некоторые S не суть P	Существует такой объект x, который обладает свойством S и не обладает свойством P.

 

Примерами категорических суждений могут являться утверждения (табл.2).

Таблица 2

Название суждения	Пример
Общеутвердительное	«Все квадраты являются параллелограммами» «Все трапеции являются четырехугольниками»
Частноутвердительное	«Некоторые треугольники - равносторонние» «Некоторые хорды являются диаметрами»
Общеотрицательные	«Никакой парабалоид не есть алгебраическая линия первого порядка» «Никакой треугольник не является окружностью»
Частноотрицательные	«Некоторые хорды не являются диаметрами» «Некоторые параллелограммы не являются ромбами»

Наиболее часто в геометрии встречаются  общеутвердительные или общеотрицательные суждения. В математике вместо термина «суждение» часто используется термин «утверждение». аксиома - исходное утверждение науч. теории, принимаемое без доказательства [13]. В школах учащихся знакомят с понятием аксиомы. Так, в учебнике Л.С. Атанасяна и др. «Геометрия 7 – 9» [3] об аксиомах пишут так: «Некоторые утверждения о свойствах геометрических фигур принимаются в качестве исходных положений, на основе которых доказываются далее теоремы и, вообще, строится вся геометрия. Такие исходные положения называются аксиомами».

Наиболее важным понятием для школьной геометрии есть теорема.

В книге «Педагогика математики»[26] А. А. Столяра теорема является только общеутвердительные и Общеотрицательные истинные суждения. Авторы современных учебников [6,7] также придерживаются этого мнения.

Опишем понятие теорема, через понятие утверждение. «Толковый словарь русского языка» С.И. Ожегова под теоремой понимает «утверждение, истинность которого устанавливается путём доказательства»[18].

B «Математическом энциклопедическом словаре»: «Теорема - математическое утверждение, которого установлена путём доказательства»[20].

В Логическом словаре-справочнике помещено такое определение: «Теорема (греч. Theorema рассматриваю, обдумываю) положение, утверждение, устанавливаемое при помощи доказательства, основывающегося или на аксиомах, или на доказанных уже положениях»[21].

В школьных учебниках по геометрии теорема определяется так: «В математике каждое утверждение, справедливость которого устанавливается

путём рассуждений, называется теоремой» [3].

Кратко опишем структуру, теоремы.

В теореме должно быть ясно указано: во-первых, при каких условиях в ней рассматривается тот или иной объект и, во-вторых, что об этом объекте утверждается.

В каждой теореме высказывается какая-то зависимость между понятиями, утверждается, что наличие или отсутствие некоторых свойств или признаков влечет за собой наличие или отсутствие других свойств. Например, в теореме «Сумма углов треугольника равна 180°» утверждается, что углов треугольника равная 180° влечет за собой его существование.

В.Г. Болтянский [22] в структуре теоремы выделял 3 части (рис.2).

«Структура теоремы»

Рисунок 2

По его мнению, большинство встречающихся школьном курсе математики теорем может быть записано в форме: 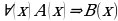, где в разъяснительной части должно быть указано, что означает переменная х, а затем пишутся два утверждения, соединенные знаком ⇒. Первое из этих утверждений называется условием теоремы, второе называется заключением теоремы. Условие и заключение теоремы представляют предикаты А(х) и B(x). Часто предикаты А и В обычно зависят не от одной переменной х, а от нескольких переменных.

Если обратиться к учебному пособию Далингера В.А. в «Обучение учащихся доказательству теорем»[22], то мы увидим, что для словесной формулировки теоремы используются 3 формы суждения:

« Формы суждений по В.А.Далингеру»

Рисунок 3

Известно, что разбор структуры теоремы будет усвоен эффективнее, когда она сформулирована в условной форме.

Условная форма теоремы позволяет определить, что характеризует данное утверждение свойство или признак. Для этого есть небольшое правило: Если объект, понятие находится в условии теоремы, то теорема выражает свойство этого понятия, если понятие или объект находится в заключении теоремы, то она выражает признак.

К примеру, теорема Пифагора: "В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов". Переформулировав теорему из категорической формы в условную, будем иметь: "Если треугольник прямоугольный, то квадрат гипотенузы равен сумме квадратов катетов". Поскольку понятие "прямоугольный треугольник" находится в условии теоремы, теорема выражает собой свойство этого понятия.

Теорема: "Если при пересечении двух прямых секущей, накрест лежащие углы равны, то прямые параллельны". Понятие "параллельные прямые" находится в заключении теоремы, а значит это теорема-признак.

Таким образом, мы выяснили, что теорема является суждением, утверждением. В свою очередь, существует четыре типа утверждений

• Общеутвердительное

• Частноутвердительное

• Общеотрицательные

• Частноотрицательные,

А сама теорема является математическим утверждением, истинность которого установлена путём доказательства. В структуре теоремы существует три части: разъяснительная часть, условие, заключение.

Так же мы выяснили, что при формулировке теорем используются три формы суждения: категорическая, условная, разделительная.

1.2.Методы доказательства математических теорем

Основную нагрузку по формированию у учащихся умения доказывать несёт курс геометрии. Д. Пойа указывал на важную роль, которую играют доказательства при построении геометрической системы: «Геометрическая система цементирована доказательствами. Каждая теорема связана с предшествующими аксиомами, определениями и теоремами каким-нибудь доказательством. Без понимания таких доказательств нельзя понять самую сущность системы»

Обратимся к Большой российской энциклопедии [2], где умозаключение- мыслительная процедура непосредственного выведения некоторого высказывания, или суждения (называемого заключением), из одного или нескольких др. высказываний (называемых посылками).

А вот в логическом словаре [21] этот термин определяется так : Умозаключение – это рассуждение, в ходе которого из одного или нескольких суждений, логически выводится новое суждение, называемое заключением или следствием.

Существуют частные и общие методы доказательств теорем. К частным методам доказательства относят метод геометрических преобразований, векторный, координатный, алгебраический методы и т. д. Но в данной работе более подробно остановимся на общих методах, которые более часто встречающиеся в школьном курсе математике, а именно синтетический, аналитический методы (нисходящий и восходящий анализ), доказательство от противного и т.д.

Среди всех методов доказательства теорем в школьном курсе геометрии основную нагрузку несет синтетический метод, ибо он является составной частью доказательства любым другим методом.

Доказательство математического предложения 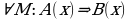называется синтетическим, если оно осуществляется по следующей логической схеме: 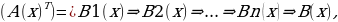^{где Т — определенная совокупность} предложенной той математической теории, в рамках которой доказывается данное предложение и ^{которой принадлежат В}1^{(х), В}2^{(х), ..., В}n^{(х), составляющих доказательство, а также суждения} А(х) и В(х).

Таким образом, при синтетическом методе доказательства теоремы цепочка силлогизмов строится так, что мысль движется от условия теоремы к ее заключению.

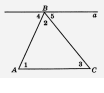
Рисунок 4

Рассмотрим синтетическое доказательство теоремы «о сумме внутренних углов треугольника».

Дано: АВС – треугольник (рис.1)

Доказать:

1+2+3=180

1. Проведем через вершину В прямую, а,

параллельную АС.

1. Рассмотрим 1 и 4; они являются накрест лежащими углами при пересечении параллельных прямых, а и АС и секущей АВ, а значит, 1=4

2. Рассмотрим 3 и 5; они накрест лежащие при пересечении параллельных прямых, а и АС и секущей ВС, а значит, 3=5.

3. Сумма 4, 2, 5 равна развернутому углу с вершиной В, т.е. 4+2+5= 180°.

4. Значит, 1+2+3=180

Теорема доказана[6].

Аналитический метод: при поиске доказательства мысль движется от заключения теоремы к ее условию. Преимущества этого метода – есть отправное звено доказательства, дополнительные построения мотивированы, увеличивается творческая активность учащихся. Недостатки – большие потери времени, искусственные дополнительные построения трудно обосновать.

Найдите углы треугольника, зная, что внешние углы при двух его вершинах равны 110° и 140°.

По условию в треугольнике нам известны только два внешних угла. Но зная, что внешний угол смежен с внутренним при этой вершине и что сумма смежных углов равна 180°, легко найдем два внутренних угла треугольника. А затем по теореме о сумме углов в треугольнике най­дем и третий угол.

Решение.

Учитель: Что нам дано в задаче?

Ребята: Нам дан треугольник, у которого внешние углы при двух вершинах равны 110° и 140°.

Учитель: Если это внешние углы, что можно о них сказать?

Ребята: Внешний угол смежен с внутренним углом при этой же вершине.

Учитель: А что мы знаем о смежных углах?

Ребята: Сумма смежных углов равна 180°. Значит, мы можем найти B и C : B = 180° – 110° = 70°, C = 180° – 140° = 40°.

Учитель: Хорошо, теперь мы знаем два угла треугольника. Как найти третий

угол?

Ребята: По теореме о сумме углов треугольника найдем  А.

A + B + С = 180°, тогда  А = 180° – (В + С),

А = 180° – (40° + 70°) = 70°.

Ответ: 70 ° и 40°.

В преподавании математики синтетический метод должен занять важ­ное место. Обучение надо вести так, чтобы учащиеся не только практически научились пользоваться синтетическим методом, но поняли его сущность и особенности, так как владение им очень важно в практической деятельности человека. Синтетическое изложение доказательств отличается исчерпываю­щей полнотой, сжатостью и краткостью. Однако вести все преподавание ма­тематики в таком стиле малоэффективно. Это связано в первую очередь с тем, что для начинающих изучать математику синтетические доказательства кажутся непонятными.

Любое аналитическое доказательство обратимо в синтетическое и наоборот. Это широко используется в учебном процессе. Технологии могут быть таковы:

1) синтетическое доказательство предваряется аналитическими поисками его плана;

2) синтетическое доказательство заменяется аналитическим, в качестве домашнего задания – изучение синтетического доказательства по учебнику;

3) при использовании лекционного метода (преимущественно за пределами курса основной школы) часто используется чисто синтетический метод доказательства.

Метод математической индукции не имеет распространения в геометрии, так как основан на свойствах множества натуральных чисел, выходит за рамки основной школы, поэтому мы не будет подвергать его специальному изучению.

Косвенное доказательство: истинность теоремы устанавливается посредством опровержения некоторых суждений, содержащихся в теореме.

Наиболее распространенный и единственно применимый в курсе планиметрии метод косвенного доказательства – доказательство от противного.

Логико-математическая сущность метода от противного: вместо прямой теоремы доказывается обратная .Отметим, что док-во методом от противного осуществляется по следующему плану :

«Сущность метода от противного»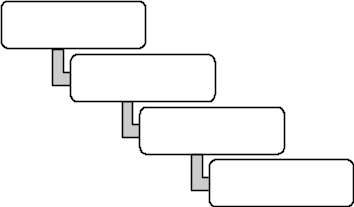

Рисунок 5

«Алгоритм доказательства от противного»

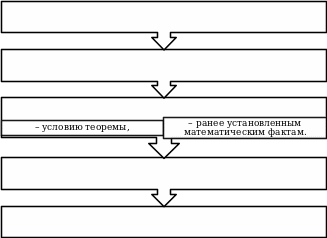
Рисунок 6

Мы описали основные логические методы доказательства теорем: прямые и косвенные, которые в свою очередь могут быть аналитическими и синтетическими, доказательствами от противного.

Можно говорить об основных математических методах доказательства теорем. В геометрии к ним можно отнести следующие базовые методы:

«Методы математического доказательства»

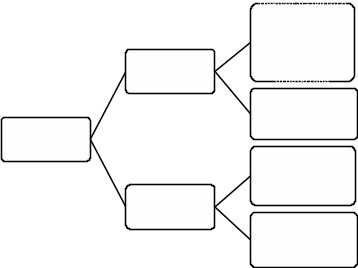
Рисунок 7

Кроме указанных базовых математических методов доказательства теорем планиметрии можно говорить о более частных методах: метод симметрии, метод поворота, векторный метод, алгебраический метод, метод подобия, координатный метод и др.

Различают два основных вида умозаключений – индукцию и дедукцию.

Индукция – это умозаключение, при котором из одного или нескольких единичных или частных суждений получают новое общее суждение. Различают два основных вида индукции – неполную и полную.

Неполная индукция – умозаключение, основанное на рассмотрении одного или нескольких, но не всех, единичных суждений.

Полной индукцией называется умозаключение, основанное на рассмотрении всех единичных и частных суждений, относящихся к рассматриваемой ситуации.

Заключение, сделанное на основе полной индукции, является вполне достоверным, полная индукция является методом логического доказательства. Однако используется этот метод редко по следующим причинам: 1) громоздкость, 2) невозможность рассмотрения всех единичных и частных суждений в силу того, что их бесконечно много.

Тем не менее, можно привести примеры использования полной индукции: при изучении вопроса об измерении вписанного угла рассматриваются все возможные случаи: 1) одна из сторон угла – диаметр окружности; 2) диаметр лежит между сторонами вписанного угла; 3) диаметр находится вне угла.

Дедукция – умозаключение, при котором из одного общего суждения и одного частного суждения получают новое, менее общее суждение.

Пример: первое суждение – общее, второе суждение – частное, новое суждение – вывод – новое, менее общее суждение.

Таким образом, сущность дедукции состоит в том, что данный частный случай подводится под общее положение.

Дедукция является основным методом логического доказательства.

Дедуктивное доказательство теорем характеризуется логической последовательностью шагов, обязательностью обоснований и их ссылками на уже признанные достоверными математические факты.

Выявляя основные методы доказательства теорем, можно сделать вывод , о том что аргументы к доказательству подразделяются на прямые и косвенные. Отметим, что для прямого аргументы применимы слущующие методы доказательства теорем:

• Синтетический метод:

• Аналитический метод

• Метод математической индукции

А для косвенного доказательства:

• доказательство от противного.

• математические методы доказательства теорем.

  1. метод геометрических преобразований:

  2. метод равенства и подобия треугольников

• Метод дедукции

Глава 2. Методические особенности обучения доказательству теорем

2.1.Этапы работы с теоремами. Приемы

доказательства теорем

При изучении теорем в курсе геометрии перед каждым школьником предстоят две задачи, это узнать новое свойство или признак геометрического объекта, или связь нескольких объектов ; а так же логически обосновать истинность предлагаемых утверждений.

Для того, чтобы решить вторую учебную задачу, необходимо разделить всю работу с теоремами на этапы .

В данной работе мы опираемся на опыт Г.И.Саранцева [25]. Педагог выделяет следующие этапы изучения теорем:

1. Мотивация изучения теоремы.

2. Ознакомление с фактом, отраженным в теореме.

3. Формулировка теоремы и выяснение смысла каждого слова в формулировке теоремы.

4. Усвоение содержания теоремы;

5. Запоминание формулировки теоремы;

6. Ознакомление со способами ее доказательства;

7. Доказательство теоремы;

8. Применение теоремы;

9. Установление связей теоремы с ранее изученными теоремами. 

Зная данный универсальный алгоритм проработки любой геометрической теоремы, не так трудно становится работать с доказательством.

Безусловно, необходимо помнить об основных приемах доказательства теорем. Каждый прием, по своему, обеспечивает понимание материала учеником. Такие приемы указал В.А. Далингер в твоих трудах «Обучение учащихся доказательству теорем»[22]. Рассмотрим их детально :

Прием 1. Использование частично-поискового метода, так активизация класса происходит посредством эвристической беседы, которую ведет учитель с учащимися. Отметим, что доказательства должны соответствовать аналитико-синтетическому методу.

Прием 2.Учитель рассказывает о доказательстве теоремы, при этом редко обращается к учащимся. Так называемый объяснительно-иллюстративный метод позволяет ученикам увидеть верный ход мысли, при логическом рассуждении. Стоит помнить, что таким методом не стоит пользоваться часто, т.к. в момент объяснения ученики не смогут долго удерживать внимание, смогут устать, если доказательство затянется. Самым главным «минусом» данного метода заключается в том, что учащиеся в данный момент бездействуют, а значит, при длительном применении такого метода все обучение становится не эффективным.

Прием 3.Метод самостоятельного изучения доказательства теоремы с помощью учебника. Учитель в таком приеме объяснения выступает лишь консультантом, а основная нагрузка идет на учащихся. Однако, если работа строиться вместе с учебником , то этот метод становится схожим со вторым приемом, где ребята разбирают верный разбор доказательства, а далее доказывают по аналогии. Так же возникает еще одна трудность, ученикам виден целостный чертеж доказательства теоремы, а значит им самостоятельно необходимо выстроить весь порядок рассуждения и построения чертежа.

Для того, чтобы лучше понимать с какими определениями, приемами и формулировками встречается обучающийся, на курсе геометрии проведем анализ основных учебников геометрии, методических пособий для учителя и разработок самих учителей. Особое внимание уделим именно 7 классу, т.к именно в этот период определяются основные направления работы курса. Рассмотрим 3 основных учебника следующих авторских коллективов:

• Геометрия 7-9кл. Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б.[6]

• Геометрия 7 кл., 8кл., 9кл., Мерзляк А.Г., Поляков В.М.; под редакцией Подольского В.Е.[32,34,33]

• Геометрия 7-9 кл. Погорелов А.В.[7]

В каждом из учебных пособий мы проанализируем, каким образом представляется теорема и каковы методы ее доказательства.

Изучив первые страницы учебника геометрии Атанасян Л.С и др, выяснилось, что с первых страниц учебника авторы вводят аксиому «Через любые две точки, можно провести прямую и притом, только одну», несмотря на то , что это аксиома приводится обоснование, методом от обратного. Представим пример (рис.8) :

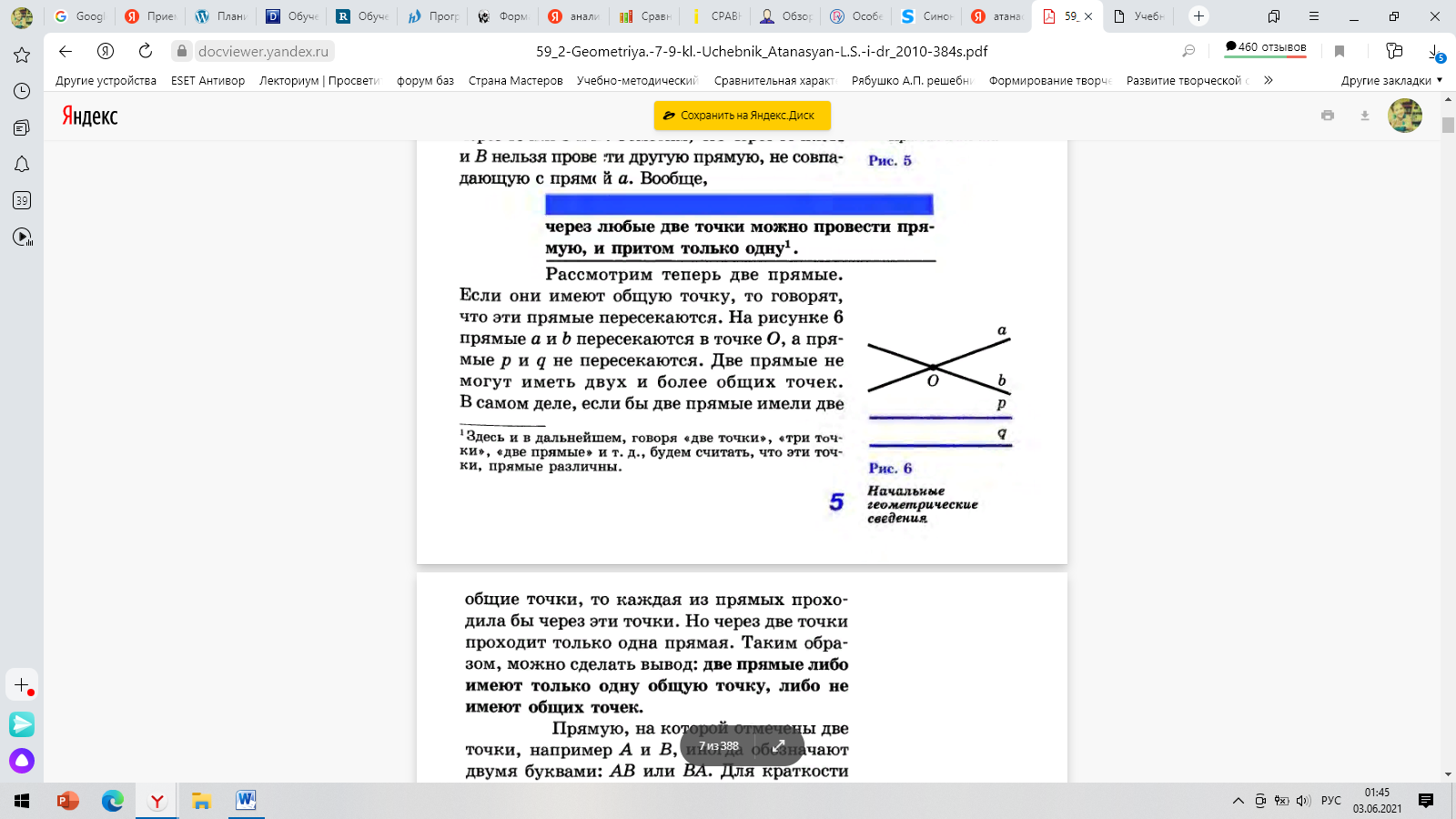
Рисунок 8

Так, с первых страниц учащимся показывают, необходимость обоснования каждого утверждения в геометрии.

Однако следующее обоснование встречается лишь в §4, в качестве решенной задачи, где обосновывается практическое решение задачи. Приведем пример (рис.9):

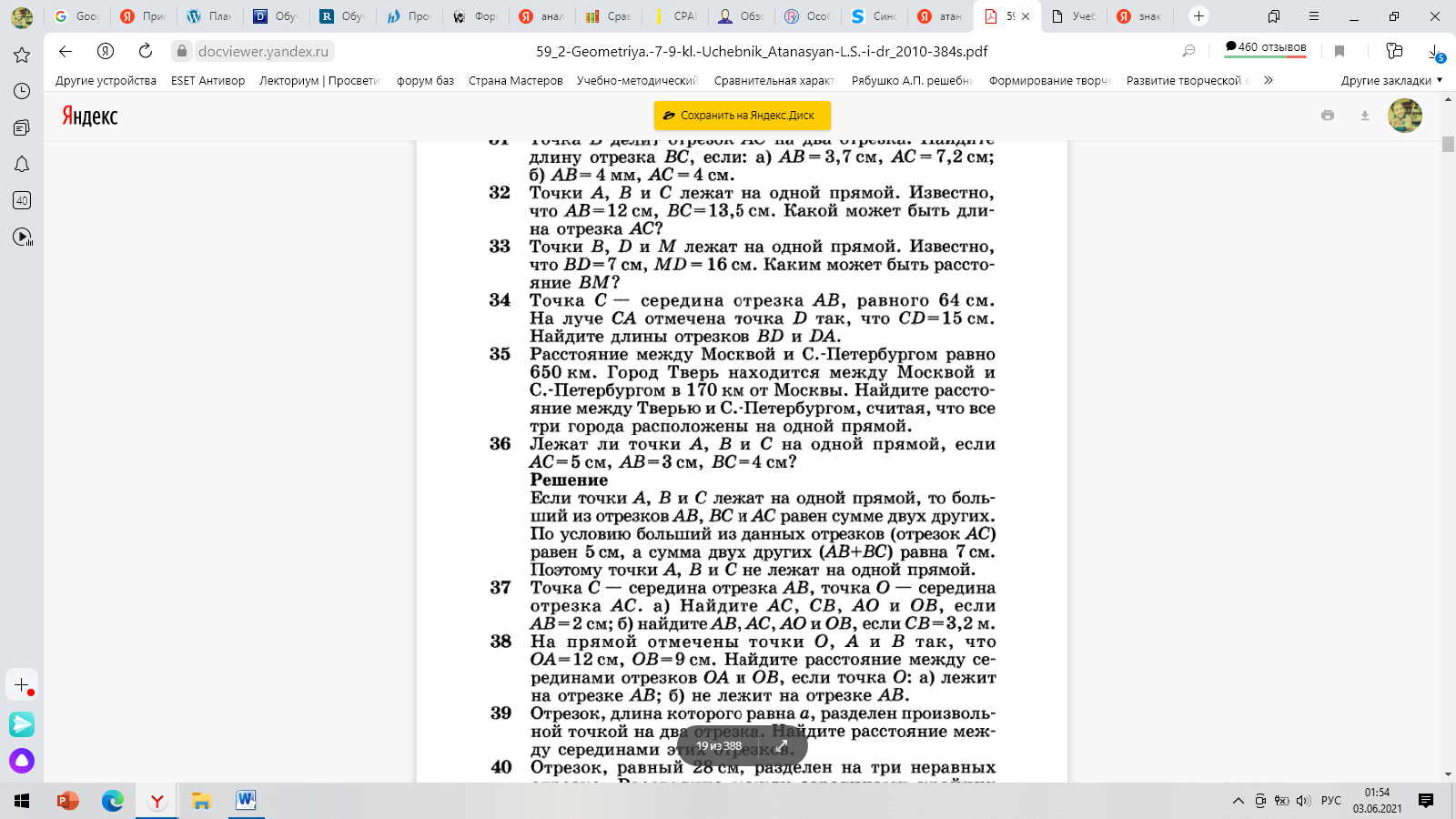
Рисунок 9

Отметим, что в данном учебном пособии задание на доказательство появляются раньше, чем само определение понятия «доказательство». Первое доказательство, где можно использовать третий прием, указанный выше, встречается на теме «Первый признак равенства треугольников». Приведем примеры заданий на доказательство:

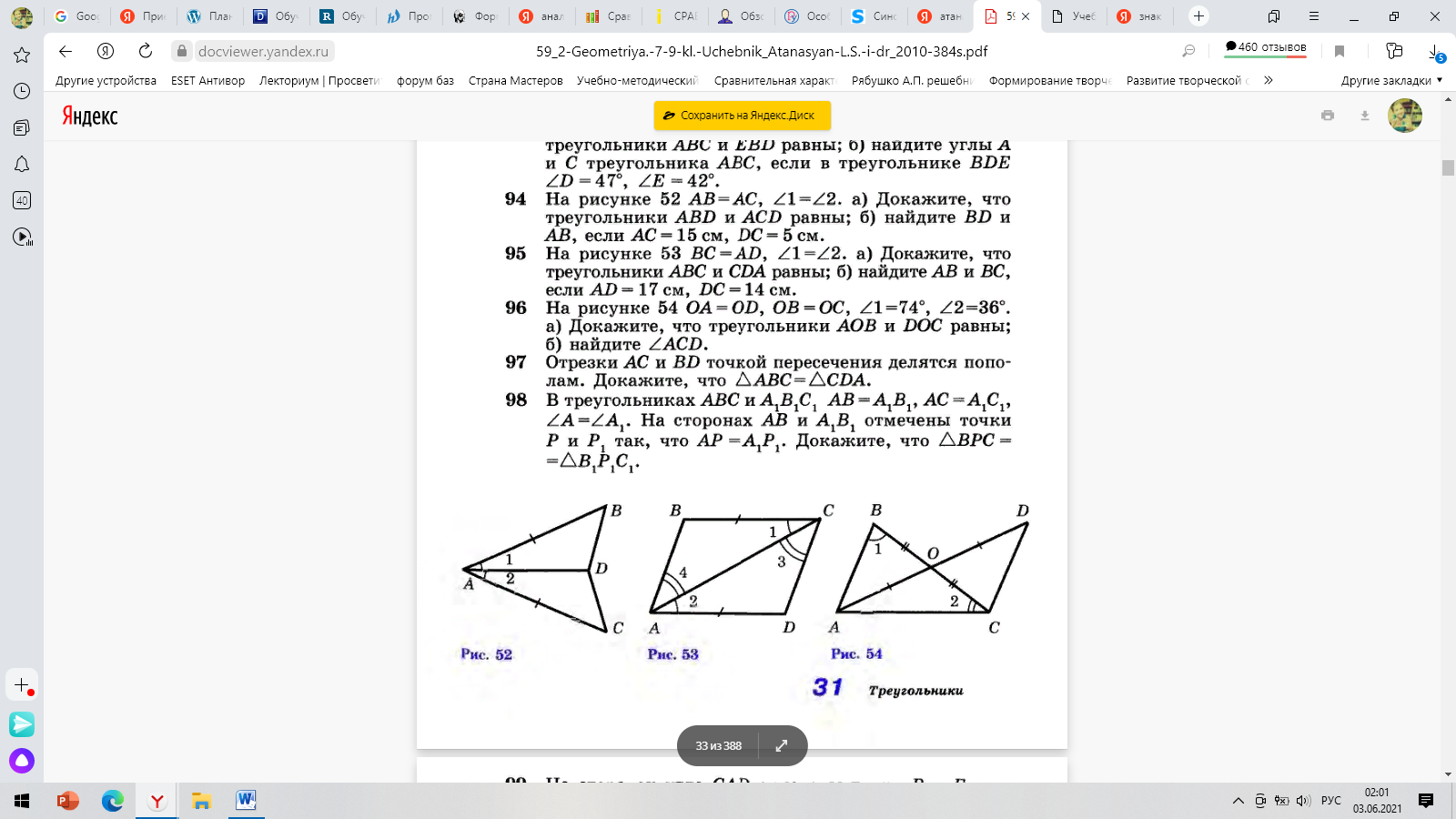
Рисунок 10

Отметим, что в учебнике не указано как правильно доказывать теоремы, оформлять задачи, как строить обоснование и на какие этапы его можно разбить.

С каждой новой темой заданий на доказательство становится все больше, приводятся различные примеры, где используются методы геометрических построений, индукции и дедукции.

Обратим внимание, что в курсе есть задачи, где уже приведены решения или доказательства. Это служит некоторой опорой и помощью в нахождение верного пути к ответу задачи , таким примером является задача № 378, где необходимо доказать, что параллелограмм выпуклый четырехугольник. (рис.11)

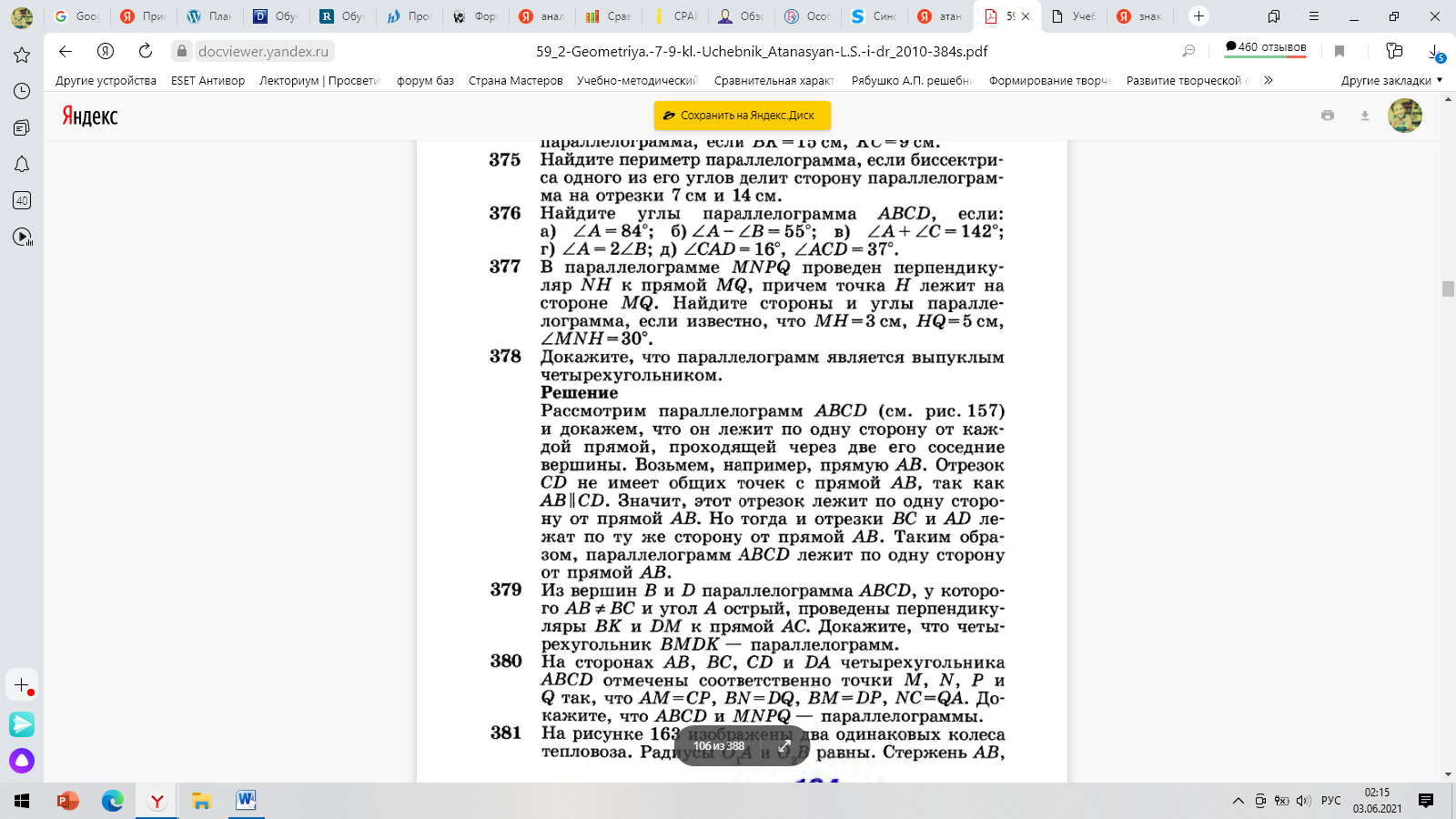
Рисунок 11

Подчеркнем, что не редко ребятам необходимо самостоятельно доказать какое-либо утверждение в теореме, опираясь на изученные теоремы и аксиомы.

Следуя далее, в курсе геометрии 8 и 9 класса, появляются задачи исследования. В них необходимо отметить и доказать верность геометрических построений.

Изучив, учебный материал, можно сделать вывод, что приведены доказательства различных теорем , заложенных в курс геометрии 7-9 классов, однако, использовать прием частично-поискового метода доказательства теорем затруднительно, т.к. представлено малое количество заданий, позволяющее это сделать.

Обратимся к методическим рекомендациям, которые прилагаются к данному учебнику[29,30,31]. Понятие доказательство вводиться во втором параграфе и указывается основная концепция работы с доказательством: « Доказательства большей части теорем курса строятся по схеме: поиск равных треугольников — доказательство их равенства — следствия, вытекающие из равенства треугольников». С методике самой работы предполагается фронтальная работа частично-поисковым приемом доказательства.

Стоит заметить, что в курсе геометрии 8 класса, большинство доказательств теорем производиться, через практическую деятельность – решение самих задач.

Анализируя последний год изучения планиметрии, можно сказать, что он нацелен на самостоятельную работу по всем видам заданий, в том числе доказательств теорем, пользуясь накопленным багажом знаний.

Подводя итог, можно сказать, что УМК Геометрия 7-9кл Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. , основной акцент делают на предметную часть – «решению задач должно быть уделено большое внимание. Все новые понятия, геометрических фигур, способы рассуждений должны усваиваться в процессе решения задач». Вышеуказанные методы и приемы доказательств теорем, смогут найти свое применение в данном УМК.

1. Рассмотрим следующий УМК Геометрия 7 кл., 8кл., 9кл., Мерзляк А.Г.Поляков В.М.; под редакцией Подольского В.Е.[14].

Анализируя данное пособие, можно отметить, что понятие аксиома, теорема и доказательство вводится в первом параграфе. Правда изначально доказательство представляют в виде логического рассуждения. Приведем пример объяснения (рис.6).

С первого параграфа учащихся просят провести обоснование на истинность своего решения. Примерами таких заданий могут служить следующие примеры:

«Правильность изготовления линейки можно проверить так. Через две точки с помощью линейки провести линию. Затем линейку перевернуть и через эти же точки вдоль того же края линейки вновь провести ещё одну линию. Если линии совпадут, то линейка изготовлена правильно. Объясните почему».

Учащемуся предстоит доказать достаточно очевидную вещь, однако он сможет воспользоваться аксиомой о точках и прямой.

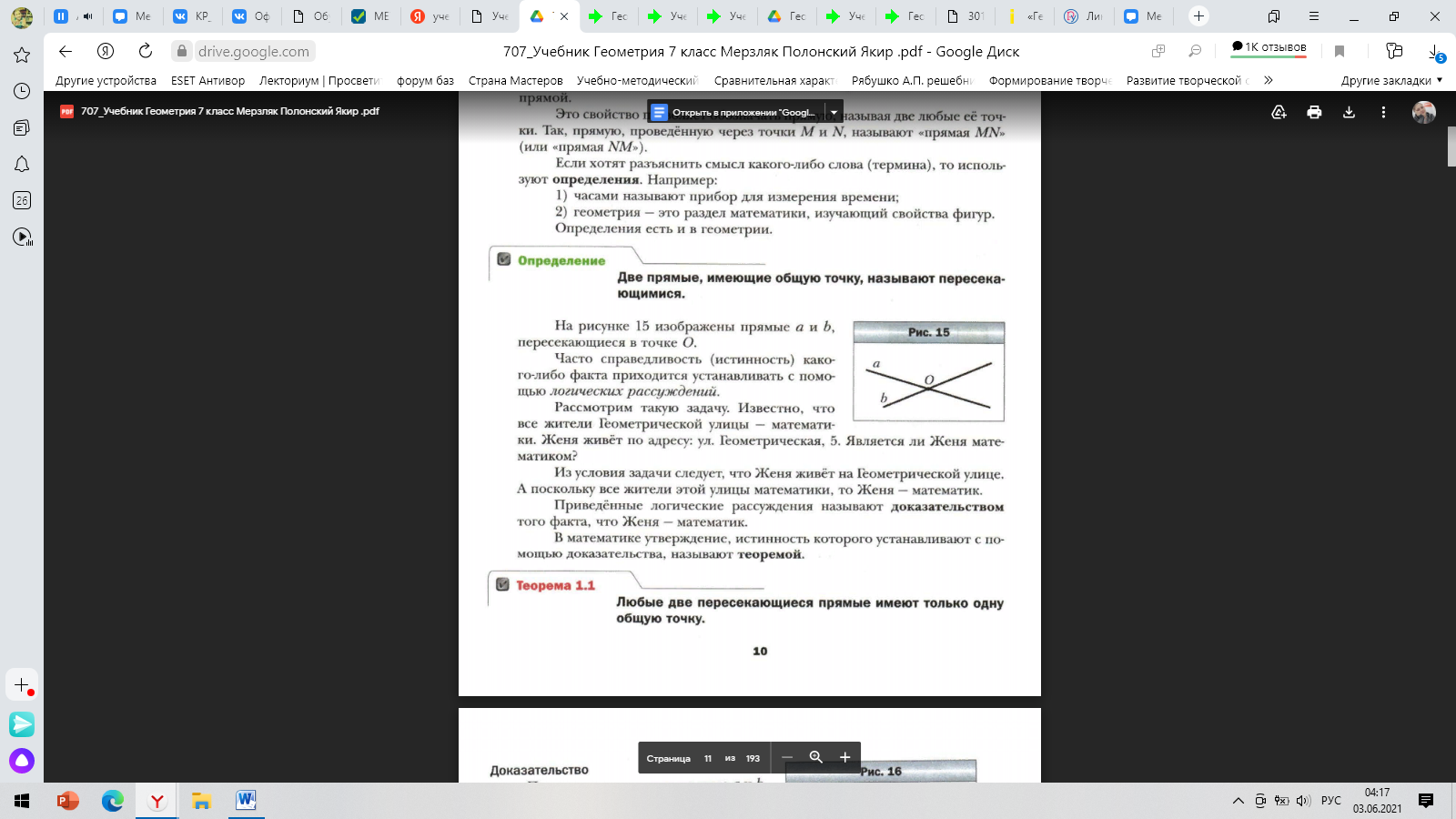
Рисунок 12

Доказательство сами теорем вводиться так же как и в предыдущем УМК, на теме смежных углов. Отличительной особенностью данного учебника является то, что существует отдельный параграф «Аксиома», описывающий историю возникновения аксиомы, и второй параграф «Теоремы», где описывают виды теорем и основы построения доказательств во второй. Так например, рассматриваются части теоремы (условие, заключение), о видах, например теоремы-признаки и теоремы-следствия. Важным аспектом является раскрытие метода доказательств – «метод от противного» и метод геометрического построения.

Отдельной особенностью УМК является особое внимание к теоретическому материалу курса. В каждой главе существуют задания направленные на самостоятельную формулировку суждений и их доказательств, определение истинности сказанного. Приведем пример (рис.7)

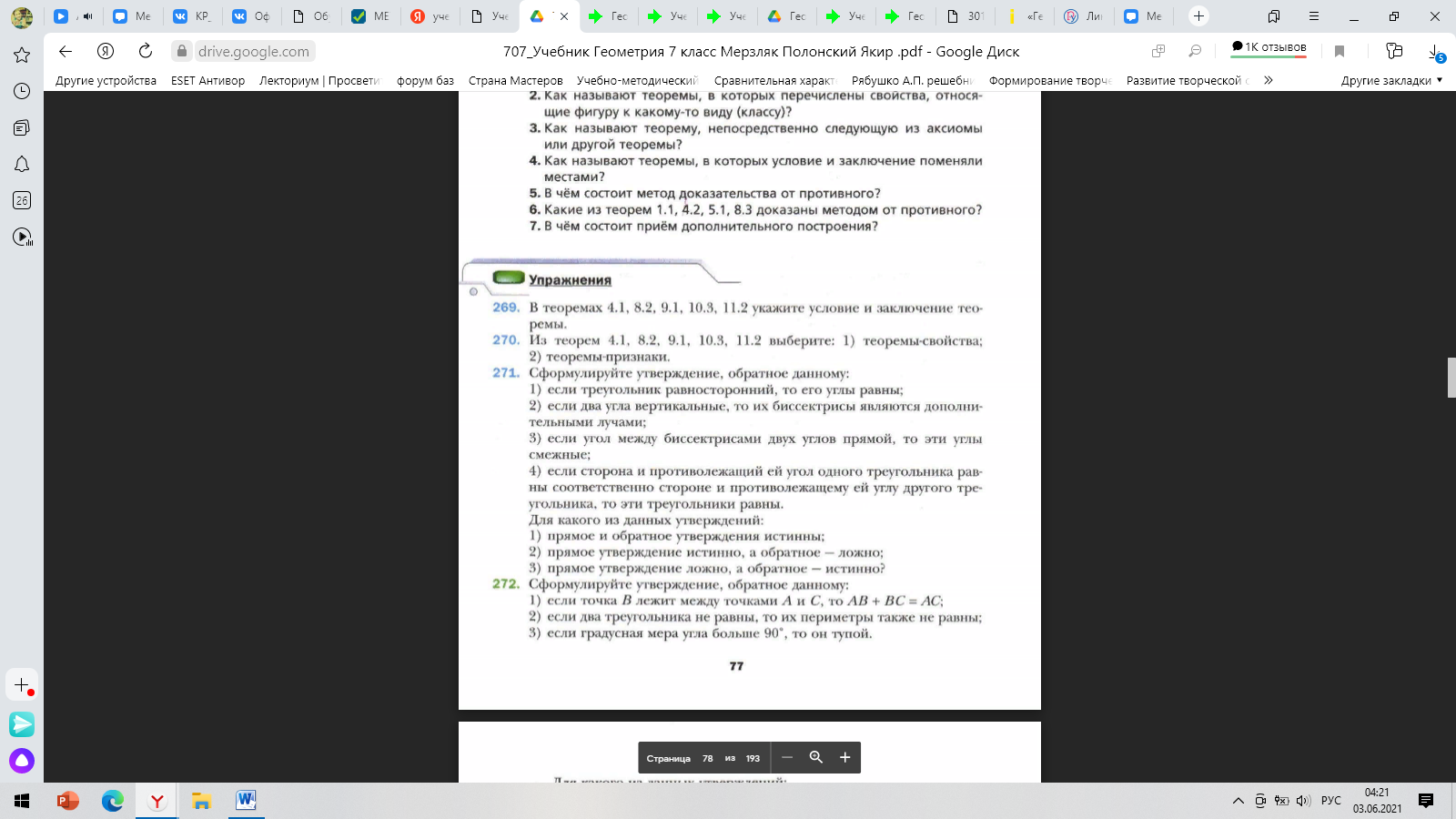
Рисунок 13

В учебнике геометрии за 8 класс вводится понятие теоремы-критерия и подробно описываются примеры таких теорем и доказательств. Отличительной особенностью всей методической линии является то, что пере изучением новой темы есть повторение предыдущего материала , что позволяет ребятам легче справиться с изучением нового материала самостоятельно.

В 9 классе учащимся самостоятельно предстоит вывести доказательство некоторых теорем, например теорему о площади параллелограмма через формулу синусов. Дополнительный материал уже несет в себе не структуру теоремы и ее доказательства, а дополнительный материал про предметный материал.

Обратимся к методическим рекомендациям данных курсов[]. В формулировке самой задачи всего курса не ставиться какой-либо особый упор на обучению доказательству. Но проанализировав все 3 методических пособия, сделаем вывод, о том , что учитель сможет уделить время для обучения ребят умению доказывать теоремы любым из приемов указанном выше.

Завершим наш обзорный анализ трем УМК . Рассмотрим УМК Геометрия 7-9 кл. Погорелов А.В.[7]. С первых страниц основные сведения геометрии представляются как определения, а далее идет задача, где необходимо обосновать ответ . Это не доказательство в чистом виде, но логические рассуждение и обоснование мыли имеется, что говорит обучающихся к пониманию обоснованности каждого определения в геометрии. Понятие доказательство вводится в первой главе, при этом нет его структуры, как и самого определения.

При изучении темы «Равенство треугольников», кратко описывается как необходимо работать с доказательством, но акцент делается, на то как использовать аксиомы и в каком порядке их писать, но не как определить порядок шагов при доказательстве .

Стоить отметить, что существует параграф, посвященный теме «Как готовиться по учебнику самостоятельно». Тут описывается примерный план работы разбора самой теоремы и примеры доказательств, некоторых формулировок.

Далее по всему курсу геометрии в 8 и 9 классах сохраняется структура самого учебника, приводится доказательство, а к нему есть готовое логическое умозаключение и обоснование. Есть задачи на доказательство для самостоятельной формулировки теоремы-признака или свойства. Например : «Докажите, что если в параллелограмме диагонали равны, то такой параллелограмм прямоугольник» .

Обратимся к методическим рекомендациям учебника [29]. В них указано, что аксиоматический метод доказательств не дается с первых уроков изучения, т.к. обучающиеся должны усвоить четкие формулировки и научиться выделять из текста главное. Метод доказательств традиционен для всех учебников геометрии – это работа с треугольниками. Работа с доказательством опирается на частично-поисковый метод или объяснительно-иллюстративный.

В курсе 8 класса основной упор на применение признаков равенства треугольников, и ребята смогут самостоятельно строить доказательства.

В 9 классе по геометрии больше применяется прием самостоятельного обоснования доказательства, с опорой на факты из 7 и 8 класса .

Подводя итог, проделанной работе , можно выяснить, что в каждом УМК применимы основные методы работы с доказательством. Однако не в каждом учебнике описана структура теоремы и тем более правила работы с ней, этапы и виды доказательств. Так, главная задача – обучить каждого учащегося умению обосновывать и доказывать теоремы ложиться на плечи учителя.

Поэтому обратимся к методическим работам учителей практиков.

Так, например, учитель математики МБОУ "Школа-гимназия"

г. Ярцево Смоленской области Демидова Л.А. на уроке «Рассуждение и доказательство от противного» начинает работу с доказательства суждений встречающихся или в алгебре или в обыденной жизни.( Приложение 1) Такой подход позволяет принять саму главную задачу –проверять каждое суждение его истинность.

Существует еще другой подход, где ребята сами могу работая в парах или в группах на начальном этапе определить необходимость доказательства своей гипотезы. Так Ведениктова С.П., учитель математики МБОУ СОШ № 14 с углублённым изучением отдельных предметов, г. Иркутска, публикует свои разработки [] с данным методом.

Таким образом , мы выяснили основные приемы методической работы учителя с доказательством на уроке геометрии, а именно

• Частично-поисковый

• Объяснительно иллюстративный

• Самостоятельного изучения

А так же выяснили, какие концепции в обучении доказательства теорем существуют в УМК по геометрии и каким образом они представлены. Так же уделили внимание некоторым методическим разработкам учителей практиков.

2.2. Методические рекомендации для работы с теоремами при изучении курса планиметрии

Анализируя, предыдущий параграф выяснилось, что в УМК недостаточно много материла посвященного структуре теоремы и ее доказательств. Основная часть методической работы ложиться на плечи учителя. Поэтому мы разберем примеры некоторых основных теорем в курсе планиметрии .

Для начала нам необходимо определиться с основными правилами доказательства теорем.

Правила доказательства теорем. Для выработки у учащихся умения доказывать теоремы необходимо:

1. Повторить предварительно с учащимися ранее изученный материал, используемый при доказательстве.

2. Перед доказательством теоремы убедитесь, что все учащиеся правильно поняли содержание теоремы, четко усвоили условие теоремы и заключение.

3. Перед тем, как приступить к доказательству, учитель должен убедить учащихся в необходимости доказательства.

4. Учащиеся должны хорошо понимать, что в процессе доказательства мы используем истинные доводы (предложения), доказанные ранее теоремы и следствия, аксиомы и определения, поэтому необходимо устно доказать

5. Проследить о наличии правильного чертежа, который будет помогать доказательству

6. Проработать каждый компонент доказательства.

7. Условие теоремы в процессе доказательства должно быть использовано полностью. Это часто помогает натолкнуть учащихся на продолжение доказательства, когда они его забывают.

8. При доказательстве целесообразно определяемое понятие заменить его определением. При изменении доказательства использовать то определение, которое наиболее соответствует характеру рассуждений (Если интересует угол между диагоналями квадрата, то квадрат – ромб, если длина диагоналей, то квадрат – прямоугольник).

9. Определение часто заменяется необходимым и достаточным признаком определяемого понятия.

10. Чтобы предупредить формализм (формальное заучивание) доказательства без достаточного осознания его, надо повторить доказательство теоремы на измененном чертеже, при других обозначениях.

Покажем выполнение данной работы на примере.

Теорема

Из точки, не лежащей на прямой, можно провести только один перпендикуляр к этой прямой.

Для начала необходимо повторить определение луч, отрезок, перпендикуляр, смежные углы, первый признак равенства

Луч- линия, имеющая начало, но не имеющая конца или часть прямой, состоящая из данной точки и всех точек, лежащих по одну сторону от неё.

Отрезок- ограниченная часть прямой [27].

Перпендикуляр - прямая, пересекающая данную прямую под прямым углом.[27]

Смежные углы - это два угла, у которых одна сторона общая, а две другие дополняют друг друга до прямой. Сумма двух смежных углов равна 180.

Первый признак равенства треугольников. Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

Теперь необходимо вернуться к формулировке теоремы и определить ее структуру.

В данной теореме определяется условие, что есть точка и прямая, следствием является то, что можно провести единственный перпендикуляр. В данном этапе необходимо убедиться, что каждый учащийся понимает употребляемые определения и связи между ними.

Рисунок 14

Определимся как будет доказывать, существуют несколько методов. Мы выбрали метод через признак равенства треугольников.

Определим чертеж , укажем прямую и очку, не лежащую на данной прямой (рис.14) Пусть точка А не лежит на прямой ВС.

Далее используем метод геометрических построений . Проведем луч ВА. Затем от луча ВС отложим угол СВD, равный углу АВС. На луче ВD отложим отрезок ВК, равный отрезку ВА (рис.15)

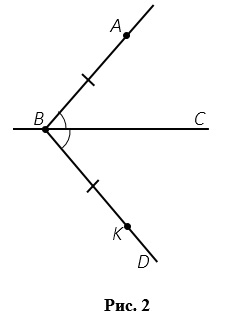
Рисунок 15

Проведем прямую АК, пусть Н - точка пересечения прямых ВС и АК (рис.16)

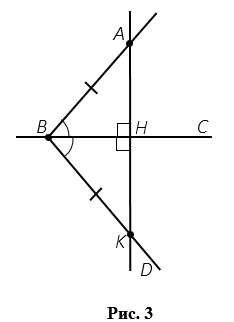
Рисунок 16

АВН = КВН по первому признаку равенства треугольников: ВН - общая сторона, ВА = ВК, АВН =КBН (по построению), ВНА =ВНD. Но ВНА и ВНD - смежные углы, тогда по свойству смежных углов ВНА +ВНD = 180°, следовательно, каждый из смежных улов прямой, т.е. ВНА =ВНD = 90°, а значит АНВС.

Мы доказали, что АН действительно является перпендикуляром, теперь докажем что он является единсвенным.

Предположим, что через точку А можно провести еще один перпендикуляр АН1 к прямой ВС, тогда получим, что две прямые АН и АН1, перпендикулярные к прямой ВС пересекаются в точке А (Рис.11).

Рисунок 17

Н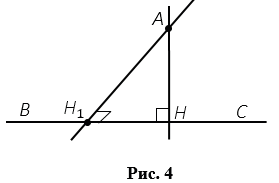
о по свойству перпендикулярных прямых, прямые АН и АН1 пересекаться не могут, значит, наше предположение неверно и через точку А можно провести только один перпендикуляр к прямой ВС. Теорема доказана.

Далее можно дать самостоятельно сформулировать обратную теорему или найти доказательство другим способом [6] . Например

Пусть А — точка, не лежащая на прямой ВС (рис. 18, а). Докажем сначала, что из точки А можно провести перпендикуляр к прямой ВС.

Отложим от луча ВС угол МВС, равный углу АВС, как показано на рисунке 18, а. Так как углы АВС и МВС равны, то первый из них можно наложить на второй так, что стороны В А и ВС первого угла совместятся со сторонами ВМ и ВС второго угла. Наглядно это наложение можно представить себе как перегибание рисунка по прямой ВС. При этом точка А совпадет с некоторой точку А₁ луча ВМ (рис. 18, б). Обозначим буквой Н точку пересечения прямых AA₁ и ВС. Отрезок АН и есть искомый перпендикуляр к прямой ВС. В самом деле, при указанном наложении (перегибании рисунка) луч НА совмещается с лучом НА₁ поэтому угол 1 совмещается с углом 2. Следовательно, ∠1 = ∠2. Но углы 1 и 2 — смежные, значит, каждый из них прямой. Итак, АН ⊥ ВС.

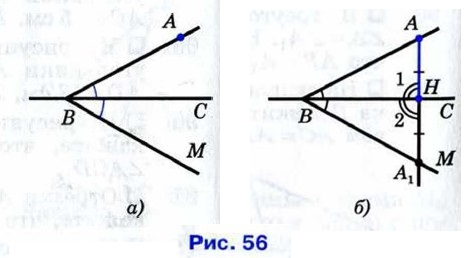
Рисунок 18

Докажем теперь, что из точки А можно провести только один перпендикуляр к прямой ВС.

Если предположить, что через точку А можно провести ещё один перпендикуляр АН₁ к прямой ВС, то получим, что две прямые АН и АН₁, перпендикулярные к прямой ВС, пересекаются (рис. 19). Но ранее в курсе геометрии было доказано, что это невозможно. Итак, из точки А можно провести только один перпендикуляр к прямой ВС. Теорема доказана.

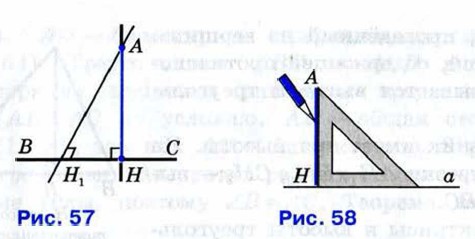
Рисунок 19

Таким образом мы рассмотрели пример доказательства на теорему из курса 7 класса геометрии , который может использоваться с любым методом и быть применим в любом уроке. Мы сформулировали основные методы работы и правила работы с доказательством теоремы

Заключение

В данной курсовой работе были освещены вопросы, касающиеся основных понятий темы, формулировок теорем, основные методы доказательства теорем.

Анализируя работу, можно сделать вывод, о том, что анализ наиболее оптимальный способ для изучения доказательств. [2].

Выяснили, что с учащимися надо проводить работу, связанную с необходимостью восстановления правильного смысла того или иного слова, понятия имеющего значение в теореме. Убедились, что целесообразно показывать учащимся различные формулировки одной и той же теоремы, которые могут им встретиться в школьных учебниках и методической литературе [5].

При преподавании геометрии, в частности доказательства необходимо использовать систему методов. Они должны уметь понимать текст, формулировать проблему, выделять закономерности, проводить исследование и подвергать сомнениям все выделенные установки и факты [5].

Так же выяснили, что использование таким таких общих методов доказательств, как анализ и синтез является одни из самых успешных инструментов для развития у учащихся потребностей обосновывать каждый шаг. Хотя первоначальное знакомство с таким обучением и требует значительной затраты времени, но в дальнейшем это все окупается. Чтобы такой урок дал эффект учителю необходимо продумывать каждый шаг, вести школьников от ступеньки к ступеньке, следить, чтобы мысли учащихся шли в нужном направлении, чтобы не ускользало от их внимания главное, чтобы все даже самые слабые ученики принимали участие в открытии нового. Не всегда, конечно, можно его применить, но там, где это, возможно, наблюдается наиболее глубокий интерес школьников, развивается логическое мышление, повышается познавательная активность.

Список использованной литературы

1. Ак­ту­аль­ные про­бле­мы обу­че­ния ма­те­ма­ти­ке и ин­фор­ма­ти­ке в шко­ле и пе­да­го­ги­че­ском ву­зе : кол­лек­тив. мо­ногр. / И. М. Смир­но­ва[и др.]. – М. : Про­ме­тей, 2017. – 238 с. : табл. – Биб­лиогр. в кон­це глав. – ISBN 978-5-906879-74-5.

2. Большая российская энциклопедия // Большая российская энциклопедия URL: https://bigenc.ru/ (дата обращения: 02.05.2021).

3. Ветошкина Е.С. Обучение учащихся проведению доказательств на уроках геометрии в основной школе: дис. канд. пед.наук : 13.00.02. - Коломна, 2004. - 196 с.

4. Виноградова Л.В. Методика преподавания математики в средней школе: учеб. пособие/ Л.В. Виноградова. – Ростов н/Д.: Феникс, 2005. – 252 с.

5. Гастева С.А., Крельштейн Б.И., Ляпин С.Е., Шидловская М.М. Методика преподавания математики в восьмилетней школе: кн. для учителя / под общей редакцией С.Е. Ляпина. – М.: Просвещение, 1965. – 743 с.

6. Геометрия : 7 класс : методическое пособие / Е.В. Буцко, А.Г. Мерзляк, В.Б. Полонский, М.С. Якир. — М. : Вен та на-Граф, 2016 — 128 с.

7. Геометрия : 7 класс: учебник для учащихся общеобразовательных организаций / А. Г. Мерзляк, В.Б. Полонский , М. Я. Якир. – М.: Вентана -Граф, 2015-193 с. 

8. Геометрия : 8 класс: учебник для учащихся общеобразовательных организаций / А. Г. Мерзляк, В.Б. Полонский , М. Я. Якир. – М.: Вентана -Граф, 2014-240 с. 

9. Геометрия : 9 класс : методическое пособие / Е.В. Буцко, А.Г. Мерзляк, В.Б. Полонский, М.С. Якир. — М. : Вентана-Граф, 2018. — 176 с.

10. Геометрия : 9 класс: учебник для учащихся общеобразовательных организаций / А. Г. Мерзляк, В.Б. Полонский , М. Я. Якир. – М.: Вентана -Граф, 2014-240 с. 

11. Геометрия, 7-9: учеб. для общеобразоват. учреждений/[Л. С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др.]. – 18-е изд. – М. : Просвещение, 2018. - 384 с.

12. Геометрия. 7-9 классы : учеб. для общеобразоват. организаций/А. В. Погорелов. – 2-е изд. – М.: Просвещение, 2014. – 240с. : ил.- ISBN 978-5-09-032301-7

13. Геометрия. Методические рекомендации. 7 класс. Учеб. пособие для общеобразоват. организаций / [Л. С. Атанасян, В. Ф. Бутузов, Ю. А. Глазков и др.]. — М. : Просвещение, 2015. — 95 с.

14. Геометрия. Методические рекомендации. 8 класс : учеб. пособие для общеобразоват. организаций / [Л. С. Атанасян, В. Ф. Бутузов, Ю. А. Глазков и др.]. — М. : Просвещение, 2015. — 110 с.

15. Геометрия. Методические рекомендации. 9 класс :учеб.пособие для общеобразоват. организаций[Л. С. Атанасян, В. Ф. Бутузов, Ю. А. Глазков др.]. — М. : Просвещение, 2015 — 96 с.

16. Гусев В. А. и др. Практикум по элементарной математике: Геометрия: Учеб. пособие для студентов физ.-мат. спец. пед. ин-тов и учителей / В. А. Гусев, В. Н. Литвиненко, А. Г Мордкович.— 2-е изд., перераб. и доп.— М.: Просвещение, 1992.— 352 с.

17. Далингер В. А. Методика обучения учащихся доказательству математических предложений: кн. для учителя / В. А. Далингер.— М. : Просвещение, 2019.— 338 с.

18. Далингер В.А. Методика работы над формулировкой, доказательством и закреплением теоремы: кн. для учителя / В.А. Далингер. – Изд-во: ОмИПКРО, 1995. – 198 с.

19. Епишева, О.Б. Технология обучения математике на основе деятельностного подхода : кн. для учителя / О.Б. Епишева. – М.: Просвещение, 2003. – 223 с. : ил, табл. – (Библиотека учителя). – Прил.: с. 181–200. – Терминолог. словарь: с. 201–211. – Библиогр.: с. 212–221. – ISBN 5-09-010905-2.

20. Закон Российской Федерации "ФГОС ООО" от 17.12.2010 № Приказ Минобрнауки России от 17.12.2010 N 1897 // Официальный интернет-портал правовой информации. – 2012– Режим доступа: свободный. – Текст: электронный

21. Игошин В.И. Математическая логика и теория алгоритмов : учеб. пособие для студ. высш. учеб. заведений / В. И. Игошин. — 2-е изд., стер. – М.: Издательский центр «Академия», 2008. – 448 с.

22. Конспект урока «Рассуждение и доказательство от противного» // https://www.yamg.ru URL: https://www.yamg.ru/metodicheskaya-rabota/metodicheskaya-kopilka (дата обращения: 02.05.2021).

23. Логический словарь-справочник // Bookree.org URL: https://bookree.org/reader?file=487443 (дата обращения: 02.05.2021). – Режим доступа: свободный. – Текст: электронный

24. Лященко Е. И. Лабораторные и практические работы по методике преподавания математики[Текст] / Е. И. Лященко, К. В. Зобкова, Т. Ф. Кириченко[и др.] ; под. ред. Е. И. Лященко. — М. : Просвещение, 1988. — 223 с.

25. Математический энциклопедический словарь // Bookree.org URL: https://bookree.org/reader?file=770058&pg=1 (дата обращения: 02.05.2021). – Режим доступа: свободный. – Текст: электронный

26. Методика обучения геометрии[Текст]: учеб. пособие для студентов бакалавриата вузов по направлению "Пед. образование" (профиль "Математика") / Г. И. Саранцев. - Казань: Центр инновац. технологий,2011. -220 с.: ил. - Библиогр. в конце глав. -ISBN 978-5-93962-493-0.

27. Методика обучения математике. Обучение учащихся доказательству теорем : учеб. пособие для СПО / В. А. Далингер. — 2-е изд., испр. и доп. — М. : Издательство Юрайт, 2018. — 338 с.

28. Методика преподавания математики в средней школе: Общая методика: Учеб. пособие для студентов пед. ин-тов по физ. мат. спец. / А. Я. Блох, В. А. Гусев, Г. В. Дорофеев и др.; Сост. В. И. Мишин. – М.: Просвещение, 1987. – 416 с.

29. Методическая разработка урока «Некоторые свойства прямоугольного треугольника». Урок доказательства теоремы. // Открытый урок URL: https://urok.1sept.ru/articles/671681 (дата обращения: 02.05.2021).

30. Ожегов,С.И. Толковый словарь русского языка[Текст] : 72500 слов и 7500 фразеологических выражений / С. И. Ожегов, Н. Ю. Шведова ; Российская АН, Ин-т рус. яз., Российский фонд культуры. - 2-е изд., испр. и доп. - Москва : Азъ, 1994. - 907,[1] с.; 27 см.; ISBN 5-85632-0077

31. Повторим математику. Учимся доказывать теорему. Режим доступа: http://viripit.ru/Pag1_3.htm (дата обращения 01.05.2021) – Текст: электронный

32. Погорелов, А.В. Аналитическая геометрия [Текст]:[Учебник для вузов]. - 3-е изд. - Москва : Наука, 1968. - 176 с. 

33. Саранцев, Г.И. Методика обучения математике в средней школе : учеб. пособие для студентов математ. специальностей пед. вузов и ун-тов : учеб. пособие для студентов вузов, обучающихся по специальности 032100 Математика / Г.И. Саранцев. – М.: Просвещение, 2002. – 223 с. – (Учебное пособие для вузов). – Библиогр. в конце гл. – ISBN 5-09-010148-5.

34. Столяр, А. А. Педагогика математики[Текст] : Курс лекций. - Минск : Вышэйш. школа, 1969. - 368 с

35. Теория и методика обучения математике: общая методика : учеб. пособие / Е. А. Суховиенко, З. П. Самигуллина, С. А. Севостьянова, Е. Н. Эрентраут. − Челябинск: Изд-во «Образование», 2010. − 65 с.

36. Хинчин, А. Я. Педагогические статьи : [статьи] / А. Я. Хинчин ; под ред. Б.В.Гнеденко. – М. : Изд-во Акад. пед. наук РСФСР, 1963. – 202, [2]с.

37. Частично-поисковый метод. Режим доступа: http://edu2.tsu.ru/html/1939/text/f2_2_s8.html (дата обращения 18.04.21)

38. Шарыгин И. Ф. Геометрия. 7—9 кл. — М.: Дрофа, 1997. — 352 с.

Приложение 1

Урок геометрии Демидовой Л.А. в 7 классе

«Рассуждение и доказательство от противного»

Место урока: пятый урок в теме « Параллельные прямые» Тип урока: урок усвоения нового материала.

Цель урока: сформировать у обучающихся знание о методе рассуждения и доказательства от противного и умение применять ориентировочную основу действия (ООД)

«доказательство от противного» в различных областях деятельности. Осуществлять косвенное доказательство (доказательство «от противоречащего», т.е. устанавливать истинность тезиса посредством доказательства ложности противоречащей ему мысли (антитезиса).

План урока.

I. Организационный момент.

II. Актуализация знаний (подготовка обучающихся к активному сознательному усвоению).

Разбор понятий, составляющих тему (фронтальное повторение)

Рассуждение – ряд мыслей, суждений, умозаключений на определённую тему, изложенных в логически последовательной форме. Цель рассуждения – получение нового знания о предмете или явлении.

Суждение – мысль, умозаключение, выражаемое повествовательным предложением и являющееся истинным или ложным.

Доказательство – рассуждение, устанавливающее истинность какого – либо утверждения путём приведения других утверждений, истинность которых уже доказана. Цель доказательства – установить истинность какого – либо утверждения.

«От противного» - от противоположного; от высказывания, противоположного по смыслу данному; от отрицания высказывания.

Итак, наша цель?

Научиться рассуждать и доказывать утверждения способом «от противного».

2. Разминка.

Задание: Составьте отрицание высказывания (ответы вписать в карточки)

ООД: используем частицу «не», глагол « не является», выражение «неверно, что …

1. Предмет геометрию начинают изучать в 7 классе.

2. Сегодня воскресенье.

3. Число а – чётное.

4. Число 135 делится на 2.

5. Число 25 – нечётное.

6. Число 48 – нечётное.

7. Число а меньше 10.

8. Число 5 меньше 10.

9. Треугольник АВС – равнобедренный.

10. Этот угол является прямым.

11. График прямой пропорциональности проходит через начало координат.

(Обсуждение результатов фронтально (слайд)

В каких случаях можно определить, истинно или ложно высказывание – отрицание?)

III. Этап усвоения новых знаний.

1. Постановка проблемы (беседа). (Предлагаются ситуации)

Первая: «Был сильный ураган: ветер ломал деревья, срывал крыши; на море поднимались сильные волны».

Вопрос: Что утверждается в этом предложении? Как автор доказывает своё утверждение? Вывод: признаки урагана подтверждают истинность высказывания. Вторая: «Этот предмет не является магнитом. Если бы это был магнит, он бы притягивал к себе металлические предметы, а он не притягивает»

Вопрос: Что утверждается в этом предложении? Как автор доказывает своё утверждение?

Вывод: Автор не имеет фактов, прямо указывающих, что предмет не является магнитом. Он доказывает это не прямо. А предполагает противоположное: предмет – магнит. Рассуждая, он приходит к противоречию между наблюдением и свойством магнита. Это противоречие опровергает его предположение. А поскольку отрицание факта неверно, то верен сам факт: предмет – не магнит.

(Практическая работа с предметами: магнит и др. предметами).

Итак. Проблема: Бывают ситуации, в которых для установления истинности (для доказательства) нет прямых фактов.

1. Решение проблемы: рассуждение (доказательство) от противного. Примеры:

1). Докажите, что в треугольнике может быть не более одного прямого угла.

(Если бы в треугольнике было хотя бы два прямых угла, то стороны, образующие эти углы с третьей стороной, были бы ей перпендикулярны. Но тогда по теореме о двух прямых, перпендикулярных третьей, эти прямые были бы параллельны, т.е. не пересекались бы и не образовывали треугольник. Это противоречит условию: дан треугольник.

Структуируем доказательство:

Доказать, что в треугольнике не может быть более одного прямого угла.

1. Предположим противное: в треугольнике более одного прямого угла, например, два.

2. Тогда… Приходим к противоречию…

3. Следовательно, наше предположение не верно, а верно, что…

4. Фронтально, устно (создание плана действий при рассуждении (доказательстве) от противного).

План доказательства от противного (ООД «доказательство от противного»):

1. Предположить противное тому, что надо доказать.

2. Провести рассуждение, основанное на известных фактах. Привести рассуждение к противоречию с другим известным фактом.

3. Сделать вывод: предположение не верно, а верно то, что надо было доказать. (слайд);

(учащимся раздаются памятки с ООД «доказательство от противного»).

IV. Этап закрепления новых знаний и умений.

1). (работа в парах, парам раздаются задания на карточках)

1. Докажите, что вы родились не в XX веке.

2. Докажите, что число 346 не делится на 3.

3. Докажите, что число 346 не делится на 5.

4. Докажите, что число 346 не делится на 9.

5. Докажите, что число 341 не делится на 2.

6. Докажите, что вычисление выполнено неверно: 536154523 * 2598563 =54276589321

7. Докажите единственность перпендикуляра, проведённого из данной точки к данной прямой.

2). Применение ООД «доказательство от противного» для доказательства следствий из аксиомы параллельных прямых (фронтально)

Аксиома: Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной. (вспомнили, проговорили в парах)

Следствие 1. Если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую. (ООД «доказательство от противного») (фронтально, оформление в тетради)

Предлагается начало (условие), по которому учащиеся выполняют чертёж и предлагают гипотезу – заключение. (Есть ли у нас прямые факты для доказательства.

Можем ли мы сказать: Да, прямая пересечёт вторую прямую, потому что…? Нет таких фактов. Тогда пробуем доказать от противного…

Следствие 2. Если две прямые параллельны третьей прямой, то они параллельны. (ООД «доказательство от противного»)

V. Этап подведения итогов, д. з

1. Что нового узнали сегодня?

2. Когда применяют доказательство (рассуждение) от противного?

3. В чем суть способа?

4. План доказательства?

5. Новые геометрические факты?

Д/задание