| Методическая информация |
| Тип урока | Урок обобщения и систематизации знаний |
| Цели урока
| Цель урока: обобщить и систематизировать знания учащихся по данной теме, повторить методы решения иррациональных уравнений, показать исторический характер теории иррациональности, проверить уровень сформированности умений и навыков учащихся по изучаемой теме. |
| Задачи урока | образовательные: развивающие: • развитие внимания, памяти, умения рассуждать и аргументировать свои действия через решение проблемной задачи; • развитие познавательного интереса к предмету; • формирование эмоционально-положительного настроя у учащихся путем применения активных форм ведения урока; • развитие рефлексивных умений через проведение анализа результатов урока и самоанализа собственных достижений. воспитательные: • развитие коммуникативных умений учащихся через организацию групповой, фронтальной работы на уроке. |
| Используемые методы и приемы | Методы организации работы: - словесные методы (беседа, чтение), - проблемно-поисковый, -метод рефлексивной самоорганизации Формы организации работы: - парная, - коллективная (фронтальная), - индивидуальная. |
| Время реализации урока | Третий урок по теме «Иррациональные уравнения» |
| Знания, умения, навыки и качества, которые актуализируют /приобретут/ закрепят/др. учащиеся в ходе урока | Знания, умения, навыки: -учащиеся должны знать и уметь применять свойства арифметического корня, решать квадратные уравнения. - ясно, точно, грамотно излагать свои мысли в устной и письменной речи, использовать различные языки математики (словесный, символический), - проводить доказательные рассуждения, аргументировать, выдвигать гипотезы и их обосновывать; - осуществлять поиск, систематизировать, анализировать и классифицировать информацию, использовать информационные источники, включая учебную литературу. |
| Дидактическое обеспечение урока | - карточки с заданиями, - карточки с практическим заданием по теме. |
| Список учебной и дополнительной литературы | Алгебра и начала математического анализа. 10-11 классы: учеб. для общеобразоват. учреждений: базовый уровень/ [Ш.А. Алимов, Ю.М. Колягин и др.]. –М.: Просвещение, 2013г. Самостоятельные и контрольные работы по алгебре и началам анализа для 10 – 11 кл. / А.П. Ершова, В.В. Голобородько. – М.: Илекса, 2005. Математика. 10-й класс. Тесты для промежуточной аттестации и текущего контроля: учебно-методическое пособие. Под ред. Ф.Ф. Лысенко, С.Ю. Кулабухова. / Ростов-на-Дону: Легион-М, 2011. |
| Ход и содержание урока |
| 1. Мотивация учебного процесса (1 мин)
| Здравствуйте, ребята! Сегодня у нас обобщающий урок по теме «Решение иррациональных уравнений». Повторяем, обобщаем, приводим в систему изученные виды, методы и приемы решения иррациональных уравнений. Записываем тему урока «Решение иррациональных уравнений» Перед вами стоит задача – показать свои знания и умения по решению иррациональных уравнений. |
| 2. Актуализация теоретических знаний (7 мин) | Преподаватель: Что такое иррациональные уравнения? (Уравнения, в которых переменная содержится под знаком корня) История развития теории иррациональности знает много ученых – исследователей. Назовем некоторых из них, отвечая на вопросы теории, которая является фундаментом, для решения иррациональных уравнений. Первый кроссворд.
1. Что требуется для полученных значений переменной при решении иррациональных уравнений? (проверка)
2. Способ, которым проводится проверка решений иррациональных уравнений (подстановка)
3. Как называется знак корня? (радикал)
4. Сколько решений имеет уравнение х2 = а, если, а 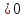 (ноль) (ноль) 5. Как называется уравнение, в котором под знаком корня содержится переменная? (иррациональное)
6. Как называется корень второй степени? (квадратный)
Получилось имя Евклид. Евклид – это великий ученый, он жил в 3 веке до нашей эры в Древней Греции. Известно, что он был приглашен в Александрию царем Птолемеем I для организации математической школы. Он был человеком мягкого характера, очень скромного, но независимого. Он сказал, что познание мира ведет к совершенствованию души. Предлагаю эти слова взять эпиграфом нашего урока. Необходимость введения иррациональных чисел была описана в работе Евклида, по которой потом занимались все творцы современной математики: Декарт и Ферма, Ньютон и Лейбниц, Колмогоров и Понтрягин.
Как называлась эта древняя книга, которая оказала наибольшее влияние на развитие европейской цивилизации? НАЧАЛА.
Именно в этом труде Евклид впервые заявил о необходимости введения новых неизведанных чисел. Понятие иррациональности ассоциируется с изображением корня. Греческие математики вместо слов “извлечь корень” говорили “найти сторону квадрата по его заданной величине (площади)”. Знак корня впервые появился в 1525 году. За это время его изображение менялось. Кто ввел это изображение? Об этом мы узнаем, ответив на следующие вопросы. Второй кроссворд.
1. Сколько решений имеет уравнение х2=0. (одно)
2. Корень какой степени существует из любого числа? (нечетной )
3. Как называется корень третьей степени? (кубический)
4. Сколько решений имеет уравнение х2=а, если а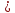 0? (два) 0? (два)
5. Как называется корень уравнения, который получается в результате неравносильных преобразований? (посторонний)
6. Корень, какой степени существует только из неотрицательного числа? (четной)
Итак, впервые изображение корня ввёл Декарт, французский ученый. Им положено начало исследования важных свойств алгебраических уравнений. Третий кроссворд.
Кто же ввел современное изображение корня? Ответим на следующие вопросы.
1. Как называется равенство двух алгебраических выражений? (уравнение)
2. Как называют значение переменной, при котором уравнение обращается в верное числовое равенство (корень)
3. Какая черта личности поможет при решении иррациональных уравнений? (трудолюбие)
4. Какой должен быть взгляд на уравнения, чтобы, не вычисляя сказать ответ? (пристальный)
5. Как называют уравнения, если они имеют одни и те же корни или не имеют корней вообще? (равносильные)
6. Как называется иррациональное выражение, содержащее противоположное арифметическое действие? (сопряженное)
Это Ньютон – английский физик, открывший основные законы природы, законы Ньютона. Он ввёл современное изображение корня.
Мы повторили теорию решения иррациональных уравнений, которая является фундаментом для познания мира. Преподаватель: -Давайте вспомним, какие основные методы решения иррациональных уравнений вы знаете? (Метод возведения в степень, равную показателю корня, метод пристального взгляда, метод введения новой переменной) |
| 3.Блоки уравнений (15 мин) | Методы решения иррациональных уравнений. Преподаватель: Сейчас вам предлагается решить первое иррациональное уравнение: 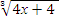 = -2 = -2
Преподаватель: Каким методом будем решать данное уравнение (Методом возведения в степень, равную показателю корня) Расскажите алгоритм решения методом возведения в степень, равную показателю корня.
1) Возведём обе части уравнения в степень, равную степени корня.
2) Решим полученное уравнение.
3) Выполним проверку. Решение: возведем в третью степень обе части уравнения, получим 4х+4= -8 4х=-8-4; 4х=-12;х=-12:4=-3. Так как степень корня нечетная, проверку делать не будем. Ответ: -3
Преподаватель: Решим уравнение 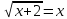 . . Возведём обе части уравнения в квадрат: 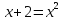 , ,
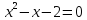 . .
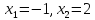 . . Проверка: 1) Если x=2, то 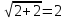 , -верно; , -верно; 2) Если x=-1, то 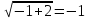 , ложно. , ложно. Ответ: 2. Преподаватель: Какой метод предполагает устное решение? (Метод “пристального взгляда”)
7. На каких свойствах иррациональных выражений основан этот метод? (Значение арифметического корня четной степени есть величина неотрицательная, а значит сумма, произведение и частное таких выражений будет величина неотрицательная. Предлагается решить несколько иррациональных уравнений устно. 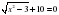 ; ; 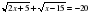 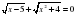 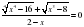
Преподаватель: Развиваем алгебраическую зоркость. На доске записано решение иррационального уравнения, в котором допущена ,,стандартная,, ошибка. Найдите её. | 1. Решить уравнение: 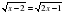
Решение: 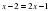
Ответ: -1 | Ошибка. Ученик возвел в квадрат формально. На области 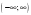 обе части уравнения не определены. обе части уравнения не определены. 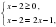 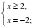
Ответ: нет решений. |
Преподаватель: Решите уравнение методом введения новой переменной: 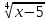 = 30- = 30- 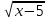
Введём новую переменную. Пусть 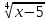 = а, а = а, а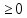 , тогда , тогда 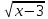 = а2. Получим уравнение а = 30 - = а2. Получим уравнение а = 30 - 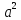 . Корни: -6 и 5. . Корни: -6 и 5. По условию подходит, а =5. 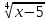 = 5. х - 5= 625; х= 630. Ответ:630. = 5. х - 5= 625; х= 630. Ответ:630. Давайте еще раз сделаем общий вывод: вспомним алгоритм решения иррациональных уравнений введением новой переменной. Алгоритм решения методом введения новой переменной: Введём новую переменную Решим полученное уравнение Найдём значение искомой переменной Выполним проверку. Преподаватель обобщает: итак, вы вспомнили основные методы решения иррациональных уравнений, которые обогатили ваш математический арсенал. В каждом методе есть свои тонкости, о которых надо помнить. Есть, конечно ряд других методов решения иррациональных уравнений. На столах у вас представлена схема, где отмечены все методы решения иррациональных уравнений. |
| 4. Практическое применение иррациональных уравнений. (5 мин) | Преподаватель: Конечно, недостаточно просто научиться решать иррациональные уравнения. Необходимо знать, где их можно ещё применить. Необходимость изучения решения иррациональных уравнений очевидна, иррациональным уравнением выражаются формулы, описывающие многие физические процессы:
• Равноускоренное движение
• 1 и 2 космические скорости
• среднее значение скорости теплового движения молекул
• период радиоактивного полураспада и другие.
А также иррациональные уравнения использует статистика Решить задачу: При движении ракеты её видимая для неподвижного наблюдателя длина, измеряемая в метрах, сокращается по закону , где  м – длина покоящейся ракеты, км/с – скорость света, а м – длина покоящейся ракеты, км/с – скорость света, а  – скорость ракеты (в км/с). Какова должна быть минимальная скорость ракеты, чтобы её наблюдаемая длина стала не более 4 м? Ответ выразите в км/с – скорость ракеты (в км/с). Какова должна быть минимальная скорость ракеты, чтобы её наблюдаемая длина стала не более 4 м? Ответ выразите в км/с Решение Найдём, при какой скорости длина ракеты станет равной 4м. Задача сводится к решению уравнения  . .
Длина покоящейся ракеты  =5м. =5м. Скорость света с=3 км/c. км/c. 5 =4; =4;  = = ; ; 1 - = =  ; ;  = =  ; ;  = = ; ; V=180000км/cРешение.Найдем, при какой скорости длина ракеты станет равна 4 м. Задача сводится к решению уравнения при заданном значении длины покоящейся ракеты  м и известной величине скорости света км/с: км/с.Если скорость будет превосходить найденную, то длина ракеты будет менее 4 метров, поэтому минимальная необходимая скорость равна км/с. Ответ: 180 000.Ответ: 180000 м и известной величине скорости света км/с: км/с.Если скорость будет превосходить найденную, то длина ракеты будет менее 4 метров, поэтому минимальная необходимая скорость равна км/с. Ответ: 180 000.Ответ: 180000 |
| 5. Самостоятельная работа в форме теста с взаимопроверкой. (10 мин) | Вариант 1. Какие из следующих уравнений являются иррациональными: а)  = 2 = 2 б) х = 1+ х = 1+ х в) у  = 2 = 2 г)  = 3 = 3 д) у2-3у = 4 = 4 2. Является ли число х = 4 корнем уравнения  = =  3.Решите уравнения: а)  = 4 = 4 б)  = -2 = -2 4. Решите уравнения. Установите соответствие. 1. = - 4; А. – 6;6. = - 4; А. – 6;6. 2. = - 3; С. Решений нет. = - 3; С. Решений нет. 3.  = 2 D. -30 = 2 D. -30 4.  =2; В. 4. =2; В. 4.
Вариант 2. Какие из следующих уравнений являются иррациональными: а)  = 1 = 1 б) х2 + 2 х+4 = 0 х+4 = 0 в) у2 – у =  +2 +2 г)  + + = 3 = 3 д) z = 1+ 2. Является ли число х = 2 корнем уравнения  = =   . Решите уравнения: . Решите уравнения: а)  = 3 = 3 б)  +2 = 0 +2 = 0 4. Решите уравнения. Установите соответствие. 1. = - 4; А. – 6;6. = - 4; А. – 6;6. 2. = - 3; С. Решений нет. = - 3; С. Решений нет. 3.  = 2 D. -30 = 2 D. -30 4.  =2; В. 4. =2; В. 4.
Ответы: 1 вариант: 1) а, в, г 2) нет 3) х=16, нет решений 4) А-4; В- 3; С-1; D-2 2 вариант: 1) а,г,д 2) да 3) х=27 ; нет решений 4) А-4; В- 3; С-1; D-2 Выполнив самостоятельную работу, ребята обмениваются тетрадями и проверяют, используя критерий: 1 -2 задание – «3» 3 задания – «4» 4 задания – «5» |
| 6. Рефлексия учебной деятельности на уроке (итог урока) (2 мин)
| Преподаватель: Сегодня мы с вами попытались обобщить и углубить знания по теме: Решения иррациональных уравнений» Проведём самооценку результатов своей деятельности, ответив на вопрос: Трудным ли для тебя был материал урока? На каком из этапов урока было труднее всего, легче всего? Что нового ты узнал на уроке? Чему научился? Работал ли ты на уроке в полную меру сил? Как эмоционально ты чувствовал себя на уроке. |
1. = - 4; А. – 6;6.
= - 4; А. – 6;6.
2. = - 3; С. Решений нет.
= - 3; С. Решений нет.
3.  = 2 D. -30
= 2 D. -30
4.  =2; В. 4.
=2; В. 4.
1. = - 4; А. – 6;6.
= - 4; А. – 6;6.
2. = - 3; С. Решений нет.
= - 3; С. Решений нет.
3.  = 2 D. -30
= 2 D. -30
4.  =2; В. 4.
=2; В. 4.
1. = - 4; А. – 6;6.
= - 4; А. – 6;6.
2. = - 3; С. Решений нет.
= - 3; С. Решений нет.
3.  = 2 D. -30
= 2 D. -30
4.  =2; В. 4.
=2; В. 4.
1. = - 4; А. – 6;6.
= - 4; А. – 6;6.
2. = - 3; С. Решений нет.
= - 3; С. Решений нет.
3.  = 2 D. -30
= 2 D. -30
4.  =2; В. 4.
=2; В. 4.







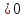 (ноль)
(ноль)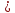 0? (два)
0? (два)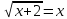 .
.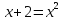 ,
,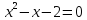 .
.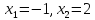 .
.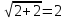 , -верно;
, -верно;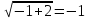 , ложно.
, ложно.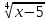 = 30-
= 30- 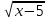
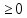 , тогда
, тогда 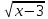 = а2. Получим уравнение а = 30 -
= а2. Получим уравнение а = 30 - 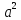 . Корни: -6 и 5.
. Корни: -6 и 5.









