Практическое занятие №2
Тема: «Разобрать с методическими комментариями типичные ошибки, допускаемые обучающимися при выполнении ГИА»
1)Тригонометрические функции.
Допускаемые ошибки:
1) ученики плохо понимают, что такое тригонометрическая окружность и как с нею связаны тригонометрические функции;
2) не владеют умением распознавать разные типы тригонометрических уравнений и применять нужные алгоритмы для их решения, выбирать решения уравнения, принадлежащие заданному интервалу;
3) допускают ошибки при определении знаков тригонометрических функций;
4) неправильно наносят точки поворота на целое число радиан;
5) вычислять значения тригонометрических выражений,
6) что такое обратные функции и как их находить;
Комментарии: Что касается свойств тригонометрических функций, то особое внимание следует обратить на:
- область определения и область значений, т.к. для синуса и косинуса есть ограничения по области значений, а для тангенса и котангенса ограничения по области определения;
- периодичность всех тригонометрических функций, наличие наименьшего ненулевого аргумента, добавление которого не меняет значение функции. Такой аргумент называют периодом функции и обозначают буквой 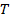 . Для синуса/косинуса и тангенса/котангенса эти периоды различны.
. Для синуса/косинуса и тангенса/котангенса эти периоды различны.
2) Тригонометрические преобразования
В преобразованиях очень часто допускают ошибку, что
tg600=2tg300; sin600=2sin300, т.е. tg2α=2tgα; sin2α=2sinα
Предупреждение этой ошибки можно проводить двумя способами:
а) с помощью графика функций.
Из графика видно, что тригонометрические функции не пропорциональны углам, поэтому sin2α ≠ 2sinα; tg2α ≠ 2tgα;
б) sin600≠2sin300; sin2α≠2sinα, т.к. 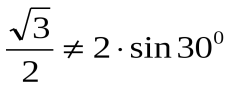 ;
; 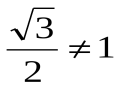
Поэтому необходимо постоянное повторение формул с помощью упражнений для устного счета и выполнения тестовых заданий.
3) Доказательство тождеств
При доказательстве тождеств чаще всего допускаются ошибки при использовании тригонометрических формул, формул зависимости между синусом и косинусом, тангенсом и косинусом, котангенсом и синусом, тангенсом и котангенсом при этом соблюдать алгоритм доказательств тождеств:
- преобразование правой части к левой;
- преобразование левой части к правой;
- установление того, что разность между правой и левой частями равна нулю;
- преобразование левой и правой части к одному и тому же выражению.
Пример:
Доказать тождество cos2 α = (1 – sin α)(1 + sin α).
Доказательство:
(1 – sin α)(1 + sin α) = 1 – sin2 α = cos2 α
Поэтому для выполнения тождественных преобразований тригонометрических выражений необходимо использовать не только данные тригонометрические тождества, но и другие формулы тригонометрии, а также алгебраические преобразования, например, действия с дробями, вынесение за скобки общего множителя, формулы сокращённого умножения.
4) Тригонометрические уравнения
В процессе формирования у школьников умений решать тригонометрические уравнения рекомендуется выделить три этапа:
1. подготовительный,
2. формирование умений решать простейшие тригонометрические уравнения и неравенства,
3. введение тригонометрических уравнений и неравенств других видов и установление приемов их решения.
При решении уравнений вида sin2x = 1,5 ученики допускают ошибки,
чтобы устранить их , надо еще раз вспомнить определение тригонометрической функции синус угла и обратить внимание на то, что синус угла – это единое целое, что это число и разрывать его нельзя.
При решении уравнения sin2x = 1,5 ученики начинают по таблицам искать угол 2x, по значению функции, забывая, что синус угла по абсолютной величине не превышает 1. Надо здесь поставить вопрос: «Какие значения принимает синус угла? Ученики дают верный ответ: Значит, sinα ≠ 1,5. Синус любого угла по абсолютной величине не больше 1, следовательно sin2х ≠ 1,5, т.е. данное уравнение не имеет решения.
5) Тригонометрические неравенства
В процессе формирования у школьников умений решать тригонометрические неравенства, также можно выделить 3 этапа.
1. подготовительный,
2. формирование умений решать простейшие тригонометрические неравенства;
3. введение тригонометрических неравенств других видов.
Допускают ошибки:
при решении тригонометрических неравенств , связанные с неправильным чтением числовых промежутков, изображенных на единичной окружности
при решении простейшие неравенства вида sinx 1, sinx x 1, cosx с помощью свойств функций синус и косинус;
при составлении двойных неравенства для дуг числовой окружности или для дуг графиков функций;
при выполнении различных преобразований тригонометрических выражений.
Учитель должен обратить внимание учащихся на различные способы выполнения задания, дать соответствующий образец решения неравенства и графическим способом и с помощью тригонометрического круга.
Решить неравенство 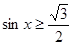
Решение неравенства с помощью круга.
Решим тригонометрическое неравенство 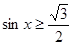 .
.
1. Начертим единичную окружность, отметим на оси ординат точку 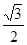 и проведем через нее прямую, параллельную оси абсцисс. Эта прямая пересечет единичную окружность в двух точках. Каждая из этих точек изображает числа, синус которых равен
и проведем через нее прямую, параллельную оси абсцисс. Эта прямая пересечет единичную окружность в двух точках. Каждая из этих точек изображает числа, синус которых равен 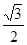 .
.
2. Эта прямая разделила окружность на две дуги. Выделим ту из них, на которой изображаются числа, имеющие синус больший, чем 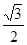 . Эта дуга расположена выше проведенной прямой.
. Эта дуга расположена выше проведенной прямой.

3. Выберем один из концов отмеченной дуги. Запишем одно из чисел, которое изображается этой точкой единичной окружности 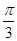 .
.
4. Для того чтобы выбрать число, соответствующее второму концу выделенной дуги, "пройдем" по этой дуге из названного конца к другому. При этом напомним, что при движении против часовой стрелки числа, которые мы будем проходить, увеличиваются (при движении в противоположном направлении числа уменьшались бы). Запишем число, которое изображается на единичной окружности вторым концом отмеченной дуги 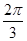 .Таким образом, мы видим, что неравенству
.Таким образом, мы видим, что неравенству 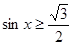 удовлетворяют числа, для которых справедливо неравенство
удовлетворяют числа, для которых справедливо неравенство 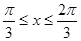 . Мы решили неравенство для чисел, расположенных на одном периоде функции синус. Поэтому все решения неравенства могут быть записаны в виде
. Мы решили неравенство для чисел, расположенных на одном периоде функции синус. Поэтому все решения неравенства могут быть записаны в виде 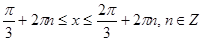
Поэтому, чтобы решить неравенство 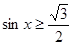 , надо составить соответствующее уравнение и решить его. Из полученной формулы найти корни
, надо составить соответствующее уравнение и решить его. Из полученной формулы найти корни 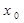 и
и 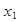 , и записать ответ неравенства в виде:
, и записать ответ неравенства в виде: 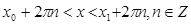 .
.
Преподавание темы «Тригонометрические функции» требует тщательного подбора содержания, средств и методов обучения, то есть разработки эффективной методики.
Изучение тригонометрических функций будет более эффективным в том случае, когда:
1) построение графиков осуществляется после исследования свойств тригонометрических функций, исходя из анализа поведения функции на числовой окружности;
2) каждое свойство функции четко обосновано и все они сведены в систему;
3) твердое знание всех формул, как в прямом, так и в обратном порядке.
Для предупреждения и устранения ошибок, необходимо больше уделять внимание решению задач и упражнений, как в школе, так и дома. Для развития и поддержания интереса к данной теме следует использовать на уроках упражнения практического характера по тригонометрии, рассмотреть тригонометрические функции в алгебраических и физических задачах.
Методика работы с задачами с ошибками может быть следующей:
Индивидуальная, парная или групповая работа. Задачи с ошибками могут быть представлены в раздаточном материале (карточки) или на слайдах презентации.
Совместное обсуждение ошибок.
Проверка результатов и подведение итогов учителем.
Примеры заданий с ошибками по многим темам можно составить самим или найти в литературных и интернет-источниках.
Черкасов О.Ю., Якушев А.Г. Математика для поступающих в ВУЗы.
Раздел пособия так и называется: «Учимся на чужих ошибках».
http://math4school.ru/rabota_nad_oshibkami.html
Раздел сайта «Мath4school» называется «Работа над ошибками», содержит большое количество примеров с решениями и подробным анализом ошибок.
















