Творческая работа "Отбор корней в тригонометрических уравнениях"

Кафедра математического образования

  Творческая работа

слушателя курсов повышения квалификации

по ДПП «Теория и методика преподавания математики»

учителя математики МОУ «СОШ п.Белоярский

Новобурасского района Саратовской области»

Дряпак Людмилы Николаевны

Руководитель: Костаева Т.В.,

зав. кафедрой математического

образования, доцент, к.п.н.

Отбор корней в

тригонометрических

уравнениях

1

2

3

4

sin х =    

y

x=(-1) k arcsin a + πk, k

Z

x

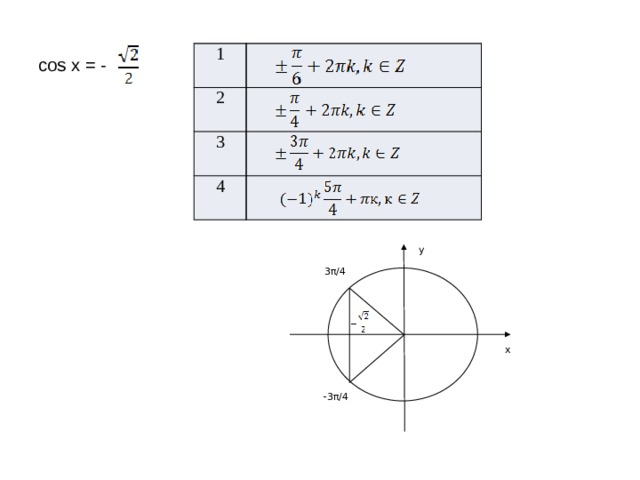
1

2

3

4

cos x = -

у

3π/4

х

-3π/4

Арифметический способ

Найти корни уравнения cos x = 0.5 , удовлетворяющие неравенству

Решение:

Проверим для полученных значений x выполнение условия

Для первой серии получаем .

Следовательно, первая серия является «посторонней».

Для второй серии получаем .

Ответ:

Перебор значений целочисленного параметра и вычисление корней

Укажите наименьший положительный корень уравнения

Если n=0, то x=10 0 Если n=0, то x=100 0

Ответ: 10

Отбор корней с использованием тригонометрической окружности

a) 2sin x(sin 2 x – 1) + cos 2 x = 0

2sin x( - cos 2 x) + cos 2 x = 0

cos 2 x( - 2sin x + 1) = 0

cos 2 x = 0 -2sin x + 1 = 0

cos x = 0 sin x = 1/2

Z x 2 =(- 1) k π/6 +πk, k

x 1 = π /2 + π n, n

Z

б) ищем корни, принадлежащие промежутку [-7π/2; -2π]

Z x 2 =(- 1) k π/6 +πk, k

Ответ: a) x 1 = π /2 + π n, n

Z

б) -7π/2, -19π/6, -5π/2

2 ) Сколько корней имеет уравнение?

ОДЗ:

Ответ: 5 корней.

Указание: решать уравнение не нужно!

Отбор корней непосредственно проверкой

Дано уравнение

А) Решите уравнение.

Б) укажите корни уравнения, принадлежащие отрезку .

Решение.

А) Преобразуем уравнение:

cosx(3cosx-1)=0.

Получаем: cosx=0 или cosx =

Б) Произведем отбор корней.

Если n=-1, то

Если

Если

Если

2.

При n=0 в серии содержится корень

принадлежащий отрезку .

При n=0 в серии содержится корень

принадлежащий отрезку .

.

.

Ответ: a)

б)

Отбор корней с использованием графиков функций

а) Решите уравнение .

б) Найдите все корни этого уравнения, принадлежащие промежутку .

Решение.

А)

Корни уравнения:

б) ) Корни, принадлежащие промежутку , отберем по графику . Прямая у=0 (осьОх ) пересекает график в единственной точке , абсцисса которой принадлежит промежутку .

пересекает график ровно в двух точках, абсциссы которых принадлежат

Прямая

Так как период функции

равен

.

, то эти абсциссы равны, соответственно,

и

.

содержатся три корня:

В промежутке

.

Ответ: а )

.

б)

Решение неравенства относительно неизвестного целочисленного параметра

и вычисление корней

Найдите число корней уравнения на промежутке

tgxcos5x+sin5x=sin6x ОДЗ: cosx

sin6x(1-cosx)=0

x=2, 3, …, 10

Ответ: 10 корней.

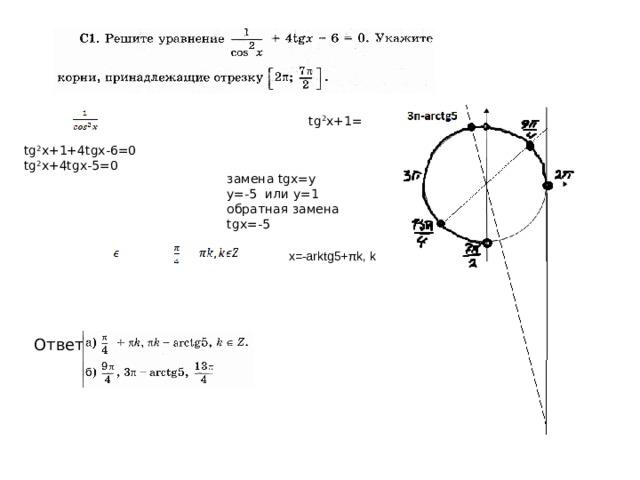
tg 2 x+1=

tg 2 x+1+4tgx-6=0

tg 2 x+4tgx-5=0

замена tgx=y

y=-5 или у=1

обратная замена

tgx=-5 tgx=1

+

x=-arktg5+πk, k

x=

Z

Ответ:

Домашнее задание