
4
29.01.22 г. Проверила замдир по УВР С. М. Асанаева
Учебная дисциплина: Математика. Продолжительность: 80 мин.
Тема: Симметрии в кубе, в параллелепипеде, в призме и пирамиде. Правильные многогранники.
Цели:
а) образовательная: развитие речи, мышления.
б) воспитательная, развивающая: формирование у обучающихся самостоятельности, наблюдательности, трудолюбия, умения сравнивать делать вывод; прививать чувства ответственности и сознательного отношения к изучаемому материалу.
Тип урока: Комбинированный урок.
Метод проведения: Сочетания фронтальной и индивидуальной работы с обучающимися.
Оборудование урока: портативный компьютер, конспект, книги.
ХОД УРОКА
Организационный момент: Приветствие группы, проверка дежурства, состояние кабинета, наличие студентов, готовность к занятиям.
Проверка знаний студентов: Проверка наличия и ведения конспектов; проверка домашнего задания; опрос.
Сообщение темы урока, постановка цели и задачи:
План:
Симметрия: определение и основные понятия.
Симметрия в кубе.
Симметрия в параллелепипеде.
Симметрия в призме.
Симметрия в пирамиде.
Представление о правильных многогранниках.
Изучение нового материала: Лекция.
(1) Однажды Л.Н. Толстой сказал: «Стоя перед чёрной доской и рисуя на ней мелом разные фигуры, я вдруг был поражён мыслью: почему симметрия приятна глазу? Что такое симметрия? Это врождённое чувство. На чём же оно основано?».
? Как вы понимаете, что такое симметрия? Где мы можем встретиться с симметрией? Приведите примеры симметрии в природе, технике, архитектуре, быту.
Совершенно верно. С симметрией мы встречаемся в природе, архитектуре, технике, быту. Мы часто видим симметричные творения природы (листья, цветы, птицы, животные) или творения человека (здания, техника) - все то, что окружает нас каждый день. В быту: молотки, рубанки, лопаты, трубы. Мы смотрим на себя в зеркало и видим, что части нашего лица симметричны друг другу. По улицам ездят автомобили, автобусы, правая и левая части которых симметричны. Таким образом, симметрия бывает не только на плоскости (кленовый лист), но и в пространстве (лицо).
В школьном курсе геометрии вы изучали симметрию на плоскости. А сегодня на уроке мы рассмотрим с вами симметрию в пространстве. Ни одно геометрическое тело не обладают таким совершенством и красотой, как многогранник. "Многогранников вызывающе мало, - написал когда-то Л. Кэролл, - но этот весьма скромный по численности отряд сумел пробраться в самые глубины различных наук".
«Симметрия» в переводе с греческого означает «соразмерность» (повторяемость). Симметричные тела и предметы состоят из равнозначных, правильно повторяющихся в пространстве частей. Особенно разнообразна симметрия кристаллов. Различные кристаллы отличаются большей или меньшей симметричностью. Она является их важнейшим и специфическим свойством, отражающим закономерность внутреннего строения.
Симметрия – это закономерная повторяемость элементов (или частей) фигуры или какого-либо тела, при которой фигура совмещается сама с собой при некоторых преобразованиях (вращение вокруг оси, отражение в плоскости).
Понятие симметрии включает в себя такие понятия, как: ось симметрии, центр симметрии и плоскость симметрии.
1) Ось симметрии - воображаемая ось, при повороте вокруг которой на некоторый угол, фигура совмещается сама с собой в пространстве (
2) Центр симметрии - это точка внутри многогранника, в которой пересекаются и делятся пополам прямые, соединяющие одинаковые элементы многогранника (грани, рёбра, углы) (С).
3) Плоскость симметрии делит многогранник на 2 зеркально равные части (Р).
4) Степенью симметрии называется совокупность всех элементов симметрии, которыми обладает данный многогранник. Например, куб обладает высокой степенью симметрии, т.к. в нём присутствуют 3 оси симметрии четвёртого порядка (3 , четыре оси симметрии 3 - го порядка (4
, четыре оси симметрии 3 - го порядка (4 , шесть осей второго порядка (6
, шесть осей второго порядка (6 В точке пресечения осей симметрии располагается центр симметрии куба. Кроме того в кубе можно провести 9 плоскостей симметрии (9Р).
В точке пресечения осей симметрии располагается центр симметрии куба. Кроме того в кубе можно провести 9 плоскостей симметрии (9Р).
( 2) Симметрия в кубе.
2) Симметрия в кубе.
Кубу свойственны все виды симметрии.
а) Центр симметрии (центр куба) - точка пресечения диагоналей куба.
б) Плоскости симметрии (9): 1) 3 плоскости симметрии, проходящие через середины параллельных ребер; 2) 6 плоскостей симметрии, проходящие через противолежащие ребра.
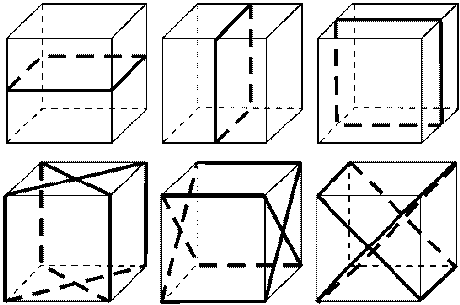
в) Оси симметрии (13): 1) 3 оси, проходящие через центры противолежащих граней; 2) 4 оси симметрии, проходящие через противолежащие вершины; 3) 6 осей, проходящие через середины противолежащих рёбер.
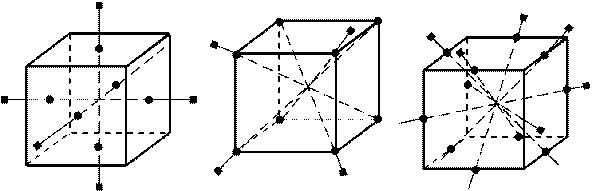

(3) Симметрия в параллелепипеде.
а) Центр симметрии - точка пересечения диагоналей прямоугольного параллелепипеда.
б) Плоскость симметрии. 3 плоскости симметрии, проходящие через середины параллельных рёбер.

в) Оси симметрии. 3 оси симметрии, проходящие через точки пересечения диагоналей противолежащих граней
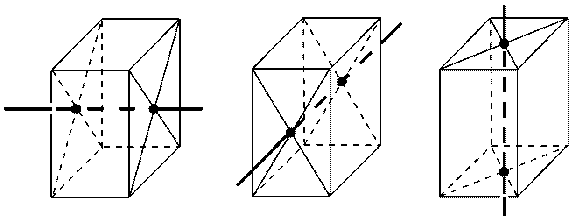
(4) Симметрия в призме.
1) Симметрия прямой призмы. Одна плоскость симметрии, проходящая через середины боковых рёбер.
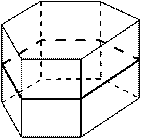
2) Симметрия правильной призмы.
а) Центр симметрии. При чётном числе сторон основания центр симметрии - это точка пересечения диагоналей правильной призмы.
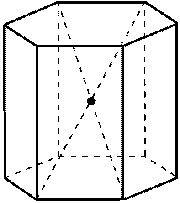
б) Плоскости симметрии: 1) плоскость, проходящая через середины боковых рёбер; 2) при чётном числе сторон основания - плоскости, проходящие через противолежащие рёбра.
1) 2)

в) Ось симметрии: а) при чётном числе сторон основания - ось симметрии проходит через центры оснований; б) оси симметрии, проходящие через точки пресечения диагоналей противолежащих боковых граней.
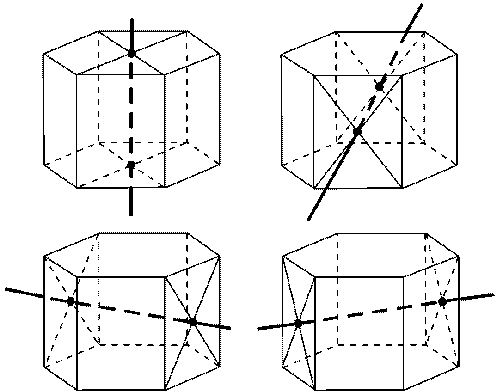

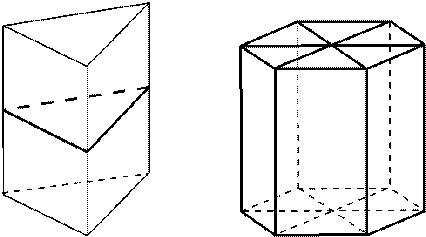
(5) Симметрия в пирамиде.
а) Плоскости симметрии: при четном числе сторон основания — а) плоскости, проходящие через противолежащие боковые ребра, и б) плоскости, проходящие через медианы, проведенные к основанию противолежащих боковых граней.

 б) Ось симметрии: при четном числе сторон основания — ось симметрии проходит через вершину правильной пирамиды и центр основания.
б) Ось симметрии: при четном числе сторон основания — ось симметрии проходит через вершину правильной пирамиды и центр основания.
(6) Самостоятельная работа по теме " Представление о правильных многогранниках". Задание: заполнить таблицу "Правильные многогранники".
| Определение правильного многогранника | Изображение | Число граней (Г) | Число вершин (В) | Число рёбер (Р) | Форма грани | Число граней, сходящихся в одной вершине | Сумма плоских углов при вершине |
| Тетраэдр - .... | 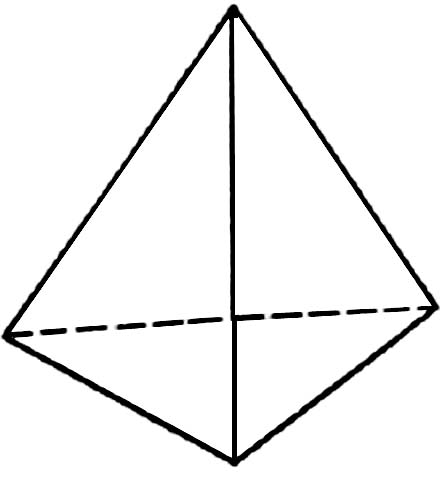
|
|
|
|
|
|
|
| Куб (гексаэдр) -... | 
|
|
|
|
|
|
|
| Октаэдр - ......... | 
|
|
|
|
|
|
|
| Икосаэдр -......... | 
|
|
|
|
|
|
|
| Додекаэдр - ...... |

|
|
|
|
|
|
|
Обсуждение и проверка заполненной таблицы.
Подведение итогов урока: Вывод о достижении цели занятия.
1) Что нового я сегодня узнал на уроке?
2) Чему научился на уроке?
3) Что вызвало трудности?









 , четыре оси симметрии 3 - го порядка (4
, четыре оси симметрии 3 - го порядка (4 , шесть осей второго порядка (6
, шесть осей второго порядка (6 В точке пресечения осей симметрии располагается центр симметрии куба. Кроме того в кубе можно провести 9 плоскостей симметрии (9Р).
В точке пресечения осей симметрии располагается центр симметрии куба. Кроме того в кубе можно провести 9 плоскостей симметрии (9Р). 2) Симметрия в кубе.
2) Симметрия в кубе.



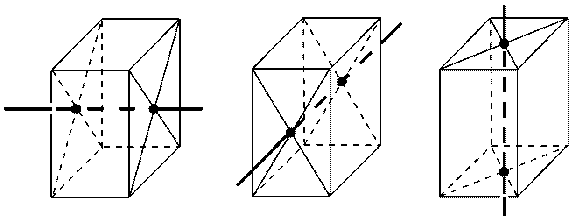





 б) Ось симметрии: при четном числе сторон основания — ось симметрии проходит через вершину правильной пирамиды и центр основания.
б) Ось симметрии: при четном числе сторон основания — ось симметрии проходит через вершину правильной пирамиды и центр основания. 













