Урок-игра в 7 классе по теме: «Признаки равенства треугольников».
Цель: Систематизация знаний, полученных на предыдущих уроках, проверить уровень усвоения
признаков равенства треугольников; показать их практическое применение на практике; развивать внимание, интерес к изучению геометрии, логическое мышление учащихся. Тип урока: Урок обобщения и систематизации знаний учащихся.
Ход урока. 1. Знакомство с правилами игры. Провести отборочный тур, класс разделиться на две группы: первая –это непосредственные участники игры, вторая—наблюдатели, которые среди участников определяют: ---самого сообразительного; ---самого внимательного; ---самого красноречивого. Кроме этого, наблюдатели по желанию могут выполнять индивидуальные задания. Правильно выполненное задание оценивается учителем, а потом приносит дополнительные баллы тому участнику, за которого данный ученик болеет.
2. Отборочный тур. Составить задачи на доказательство равенства треугольников по рисункам и устно решить их

(делим на две группы класс.)
3. Конкурс «Кто сообразительнее». Участникам необходимо ответить, правильны ли утверждения или нет, записывая против каждого утверждения «да» или «нет».
Первый раунд.
| № | Содержание вопроса | ответ |
| 1 | Через каждую точку плоскости можно провести бесконечное множество прямых. | Да |
| 2 | Две прямые пересекаются в одной точке. | Да |
| 3 | Соединяя попарно три данные точки на плоскости, всегда получим три прямые. | Нет |
| 4 | Если две различные линии на плоскости имеют две общие точки, то по крайней мере одна из них не является прямой. | Да |
| 5 | Через две различные точки всегда можно провести полупрямую, причём только одну. | НЕт |
| 6 | Для каждого угла можно построить только один вертикальный угол. | Да |
| 7 | Если один из смежных углов уменьшить в два раза, то другой угол увеличиться в два раза. | Нет |
| 8 | Через каждую точку прямой можно провести перпендикулярную ей прямую, причём только одну. | Да |
| 9 | Каждый угол, меньший прямого, острый. | ДА |
| 10 | Если три угла, образованные при пересечении двух прямых, равны, то прямые перпендикулярны. | Да |
| 11 | Каждый угол, больший прямого, тупой. | Нет |
| 12 | Если луч выходит из вершины угла, проходит между его сторонами и образует с ними равные углы, то он является биссектрисой. | Да |
| 13 | Биссектрисы вертикальных углов лежат на одной прямой. | Да |
| 14 | Если два угла равны, то смежные с ними углы также равны. | Да |
| 15 | Две прямые на плоскости или параллельны, или пересекаются. | Да |
| 16 | Если угол меньше развёрнутого, то его градусная мера меньше 180 градусов. | Да |
| 17 | Два тупых угла не могут быть смежными. | Да |
| 18 | Угол, смежный с острым, также острый. | Нет |
| 19
| Из двух углов больше тот, у которого стороны длинее. | Нет. |
После первого раунда из игры выбывает 2 участника, которые набрали наименьшее количество правильных ответов.
Второй раунд. Участники игры должны дать короткие письменные ответы на вопросы,
в конце раунда выбывает из игры ещё 2 участника с наименьшим количеством правильных ответов.
| № | Содержание вопроса | Ответ |
| 1 | Каково взаимное расположение двух прямых на плоскости, если они не имеют общих точек? | Прямые параллельны. |
| 2 | Какой наибольший угол можно образовать указательным и средним пальцем руки? | прямой |
| 3 | Как на практике показать, что треугольники равны? | Наложить друг на дру.га. |
| 4 | Какой угол образуют стрелки часов ,если они показывают 3 часа? | Прямой |
| 5 | Каким инструментом пользуются при измерении углов? | Транспортиром. |
| 6 | Какие основные геометрические фигуры на плоскости вам известны? | Точка и прямая. |
| 7 | Сколько прямых можно провести через какие-нибудь две точки на плоскости? | Одну. |
| 8 | Как называются основные свойства геометрических фигур, которые принимаются без доказательств? | Аксиомой. |
| 9 | Аксиомой, теоремой или определением является утверждение: «Две прямые на плоскости называются параллельными, если они не пересекаются»? | Определением. |
| 10 | Как называется треугольник, у которого две стороны равны? | Равнобедренным. |
| 11 | Какая теорема о вертикальных углах вам известна? | Вертикальные углы равны. |
| 12 | Как называются углы, у которых одна сторона общая, а две другие являются дополнительными полупрямыми? | Смежными. |
| 13 | Сколько прямых можно провести через одну точку плоскости? | Множество. |
| 14 | Как называется треугольник, у которого один угол тупой? | Тупоугольным. |
| 15 | Как называются различные полупрямые с общим началом и лежащие на одной прямой? | Дополнительными. |
| 16 | Как называют фигуру, состоящую из трёх точек, не лежащих на одной прямой, и трёх отрезков, попарно соединяющих эти точки? | Треугольником. |
| 17 | Как называются части, на которые разбивает плоскость прямая, которая лежит на ней? | Полуплоскостями. |
| 18 | Как называется треугольник, у которого все стороны равны? | Равносторонним. |
| 19 | По каким элементам треугольники будут равны по второму признаку равенства треугольников? | По стороне и прилежащим к ней углам. |
| 20 | Чем является медиана в равнобедренном треугольнике проведённая из вершины? | Высотой и биссектрисой. |
4 Работа в группах. Участники игры делятся на две группы. На доске выполнен рисунок, записано решение задачи. Ученикам нужно доказать, что записанный способ решения задачи правильный. Задача №1.
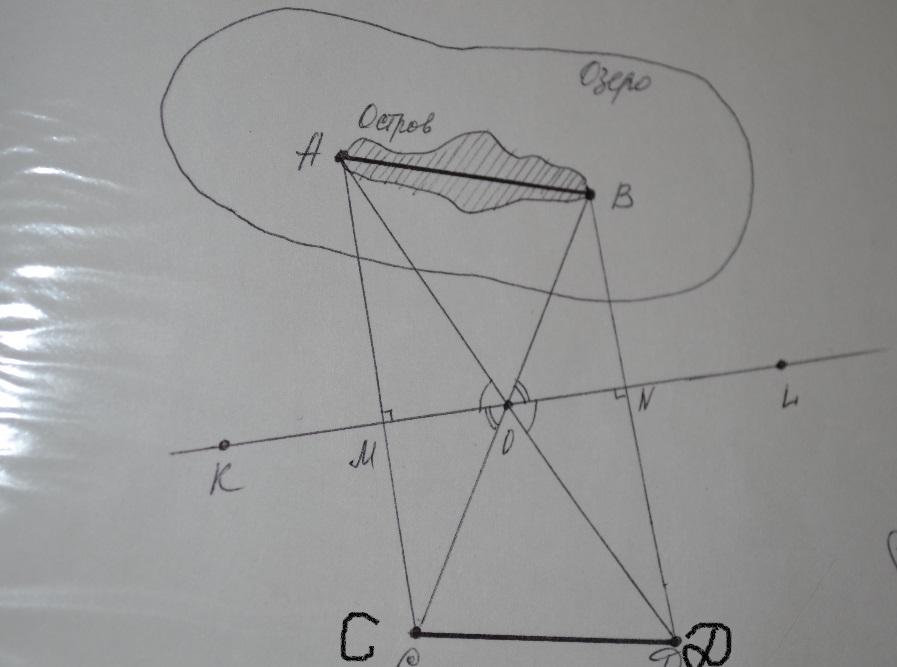 Стоя на берегу озера Свитязь , туристы решили определить длину острова, находящегося посередине озера . Для этого на берегу они забили два кола и протянули шнур KL. На прямой KL нашли такие точки М и N, что прямые АМ и BN перпендикулярны прямой KL (точки А и В конечные для острова). Потом нашли точку О, являющейся серединой МN, и такую точку С, что точки В, О и С лежат на одной прямой. Аналогично нашли точку Д . Они считают, что отрезок СД равен длине острова АВ. Докажите, что туристы выбрали правильный способ решения этой практической задачи. Решение. Треугольник МАО = треугольнику NDO по второму признаку равенства треугольников, т.к. МО=NO по построению, угол МОА равен углу NOD—как вертикальные, угол АМО равен углу DNO как прямые, тогда АО=ДО. Аналогично, доказано равенство треугольников BNO и CMO. Итак, из равенства треугольников следует, что АВ = СД.
Стоя на берегу озера Свитязь , туристы решили определить длину острова, находящегося посередине озера . Для этого на берегу они забили два кола и протянули шнур KL. На прямой KL нашли такие точки М и N, что прямые АМ и BN перпендикулярны прямой KL (точки А и В конечные для острова). Потом нашли точку О, являющейся серединой МN, и такую точку С, что точки В, О и С лежат на одной прямой. Аналогично нашли точку Д . Они считают, что отрезок СД равен длине острова АВ. Докажите, что туристы выбрали правильный способ решения этой практической задачи. Решение. Треугольник МАО = треугольнику NDO по второму признаку равенства треугольников, т.к. МО=NO по построению, угол МОА равен углу NOD—как вертикальные, угол АМО равен углу DNO как прямые, тогда АО=ДО. Аналогично, доказано равенство треугольников BNO и CMO. Итак, из равенства треугольников следует, что АВ = СД.
(Группа учеников, которая быстрее выполнит задание остаётся в игре и ей задача 2. )
Задача №2.
На острове озера Свитязь расположена база отдыха Д, которая имеет прямую телефонную связь с местным лесничеством О на берегу озера. Как не переплывая озера, определить длину телефонного кабеля, который при этом используется?
 Решение: Проведём через точку О произвольную прямую MN и прямую CD. Из точки D опустим перпендикуляр DB на прямую MN. Отложим на прямой MN отрезок АО= ОВ. Проведём прямую АС перпендикулярно к прямой MN, где С—точка пересечения прямых АС и ДО. Тогда треугольник АОС равен треугольнику ВОД-- по второму признаку равенства треугольников. Итак, ОС = ОД. А длину ОС измерить можно.
Решение: Проведём через точку О произвольную прямую MN и прямую CD. Из точки D опустим перпендикуляр DB на прямую MN. Отложим на прямой MN отрезок АО= ОВ. Проведём прямую АС перпендикулярно к прямой MN, где С—точка пересечения прямых АС и ДО. Тогда треугольник АОС равен треугольнику ВОД-- по второму признаку равенства треугольников. Итак, ОС = ОД. А длину ОС измерить можно.
Группа учеников, которая правильно и первой решит эту задачу , берёт участие в следующем конкурсе.
5. Конкурс. Среди двух учащихся, которые дошли до этого конкурса, необходимо определить того, кто преодолел все и станет победителем. Участникам конкурса предлагается сделать как можно больше « открытий» по рисунку, где АС = АК, ВС =ДК.
 Ученикам за 5 минут нужно из условия задачи получить как можно больше «открытий», например таких: 1. АВ =АД, 2. СД =КВ. 3. ВО = ДО. 4. ОК = ОС, …
Ученикам за 5 минут нужно из условия задачи получить как можно больше «открытий», например таких: 1. АВ =АД, 2. СД =КВ. 3. ВО = ДО. 4. ОК = ОС, …
6. Подведение итогов. Победителю конкурса присваивается звание «Самый умный». Его знания оцениваются оценкой---5. Наблюдатели вместе с учителем присваивают титулы: --самый сообразительный; -- самый внимательный; -- самый красноречивый. (Все участникам игры небольшие призы вручаются.)







 Стоя на берегу озера Свитязь , туристы решили определить длину острова, находящегося посередине озера . Для этого на берегу они забили два кола и протянули шнур KL. На прямой KL нашли такие точки М и N, что прямые АМ и BN перпендикулярны прямой KL (точки А и В конечные для острова). Потом нашли точку О, являющейся серединой МN, и такую точку С, что точки В, О и С лежат на одной прямой. Аналогично нашли точку Д . Они считают, что отрезок СД равен длине острова АВ. Докажите, что туристы выбрали правильный способ решения этой практической задачи. Решение. Треугольник МАО = треугольнику NDO по второму признаку равенства треугольников, т.к. МО=NO по построению, угол МОА равен углу NOD—как вертикальные, угол АМО равен углу DNO как прямые, тогда АО=ДО. Аналогично, доказано равенство треугольников BNO и CMO. Итак, из равенства треугольников следует, что АВ = СД.
Стоя на берегу озера Свитязь , туристы решили определить длину острова, находящегося посередине озера . Для этого на берегу они забили два кола и протянули шнур KL. На прямой KL нашли такие точки М и N, что прямые АМ и BN перпендикулярны прямой KL (точки А и В конечные для острова). Потом нашли точку О, являющейся серединой МN, и такую точку С, что точки В, О и С лежат на одной прямой. Аналогично нашли точку Д . Они считают, что отрезок СД равен длине острова АВ. Докажите, что туристы выбрали правильный способ решения этой практической задачи. Решение. Треугольник МАО = треугольнику NDO по второму признаку равенства треугольников, т.к. МО=NO по построению, угол МОА равен углу NOD—как вертикальные, угол АМО равен углу DNO как прямые, тогда АО=ДО. Аналогично, доказано равенство треугольников BNO и CMO. Итак, из равенства треугольников следует, что АВ = СД.  Решение: Проведём через точку О произвольную прямую MN и прямую CD. Из точки D опустим перпендикуляр DB на прямую MN. Отложим на прямой MN отрезок АО= ОВ. Проведём прямую АС перпендикулярно к прямой MN, где С—точка пересечения прямых АС и ДО. Тогда треугольник АОС равен треугольнику ВОД-- по второму признаку равенства треугольников. Итак, ОС = ОД. А длину ОС измерить можно.
Решение: Проведём через точку О произвольную прямую MN и прямую CD. Из точки D опустим перпендикуляр DB на прямую MN. Отложим на прямой MN отрезок АО= ОВ. Проведём прямую АС перпендикулярно к прямой MN, где С—точка пересечения прямых АС и ДО. Тогда треугольник АОС равен треугольнику ВОД-- по второму признаку равенства треугольников. Итак, ОС = ОД. А длину ОС измерить можно. Ученикам за 5 минут нужно из условия задачи получить как можно больше «открытий», например таких: 1. АВ =АД, 2. СД =КВ. 3. ВО = ДО. 4. ОК = ОС, …
Ученикам за 5 минут нужно из условия задачи получить как можно больше «открытий», например таких: 1. АВ =АД, 2. СД =КВ. 3. ВО = ДО. 4. ОК = ОС, … 









