Просмотр содержимого документа
«Урок в 11 классе "Задачи, приводящие к понятию производной. Геометрический смысл производной"»
№21 23.10.2017г.
Задачи, приводящие к понятию производной. Геометрический смысл производной.
11 класс.
Цели:
- обучающие: познакомить учащихся с новой математической моделью – производной функции; показать физический и геометрический смысл производной для решения физических и геометрических задач;
- развивающие: развитие памяти учащихся; развитие умений сравнивать, обобщать, правильно формулировать задачи и излагать мысли; развитие логического мышления, внимания и умения работать в проблемной ситуации;
- воспитательные: развитие познавательного интереса учащихся; развитие любознательности учащихся; развитие умений преодолевать трудности при решении математических задач; воспитание таких качеств характера, как настойчивость в достижении цели.
Тип урока. Урок «открытия» нового знания
Методы. Фронтальный опрос. Проблемный метод.
Оборудование. Проектор, учебник.
1. Проверка домашнего задания, воспроизведение и коррекция опорных знаний учащихся.
Фронтальный опрос:
Чему равен тангенс острого угла прямоугольного треугольника?
Как найти среднюю скорость движения?
Что такое приращение аргумента?
Что такое приращение функции?
2. Мотивация учебной деятельности учащихся. Сообщения темы, цели, задач урока и мотивация учебной деятельности школьников.
Понятие производной тесно связано с физикой и геометрией. Давайте выясним, почему?
Какие цели перед собой поставим? (узнать что такое производная, каков её физический и геометрический смысл)
А что мы должны сделать, чтобы достичь поставленных целей? (разобраться с задачами и понять взаимосвязь алгебра-физика и алгебра-геометрия)
3. Восприятие и первичное осознание нового материала, осмысление связей и отношений в объектах изучения
Определение 1. Пусть функция y = f(x) определена в некотором интервале, содержащем внутри себя точку x0. Дадим аргументу приращение Δx такое, чтобы не выйти из этого интервала. Найдем соответствующее приращение функции Δy (при переходе от точки x0 к точке x0 + Δx) и составим отношение . Если существует предел этого отношения при Δx → 0, то указанный предел называют производной функции y = f(x) в точке x0 и обозначают f '(x0).
Определение 2. Геометрический смысл производной состоит в следующем. Если к графику функции y = f(x)в точке с абсциссой х = а можно провести касательную, непараллельную оси у, то f '(а) выражает угловой коэффициент касательной: k= f '(а).
Показывает картинку 21.1 и 21.2
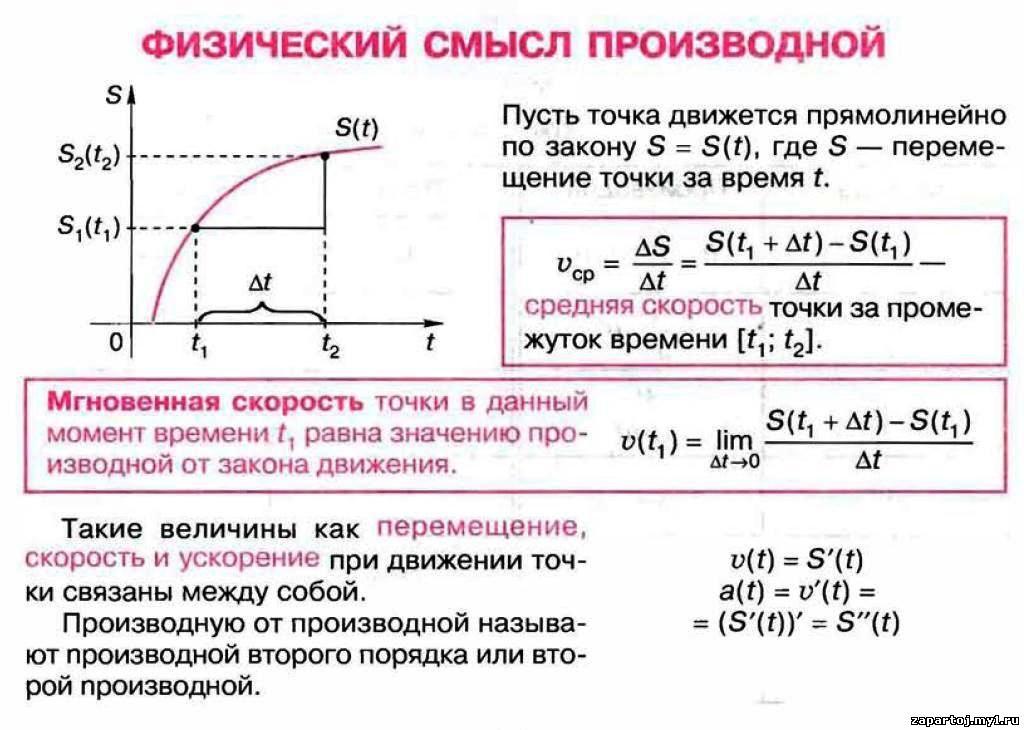
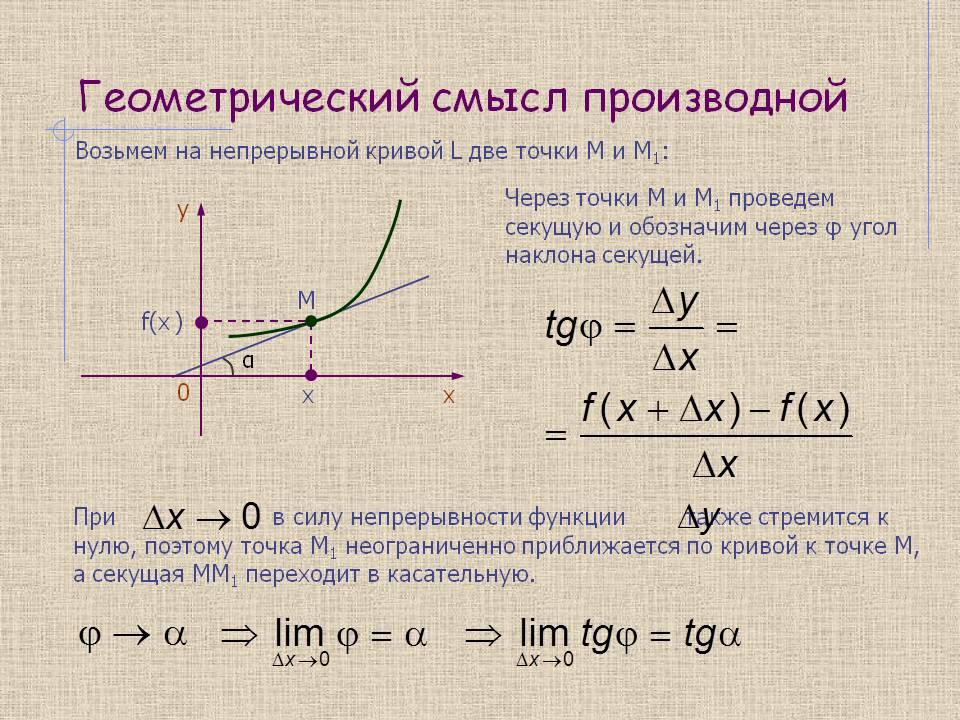
4. Первичная проверка понимания усвоенного, первичное закрепление усвоенного.
5. Подведение итогов урока (рефлексия) и сообщение домашнего задания.
Сегодня на уроке я узнал(ла)…
Трудности возникали…
Справились ли мы с поставленными задачами?
Достигнуты ли цели урока?
Сегодня я могу оценить себя….
Домашнее задание:



















