Задание 14. Вариант 19. ЕГЭ 2018 из 36 вариантов.

Задание 14. Вариант 19. ЕГЭ 2018 из 36 вариантов.

В правильной треугольной пирамиде SABC сторона основания АВ равна 60, а боковое ребро SA равно 37. Точки М и N — середины рёбер SA и SB соответственно. Плоскость a содержит прямую MN и перпендикулярна плоскости основания пирамиды.

а) Докажите, что плоскость a делит медиану СЕ основания в отношении 5:1, считая от точки С.

б) Найдите расстояние от вершины А до плоскости a.

Решение.

а) Сечение (плоскость  ) проходит через точки M и N, причем   - средняя линия. Это означает, что отрезок  . По условию секущая плоскость перпендикулярна плоскости ABC, следовательно, она пересекает плоскость ABC по уровню PQ, причем  . Таким образом, секущая плоскость представляет собой трапецию PMNQ.

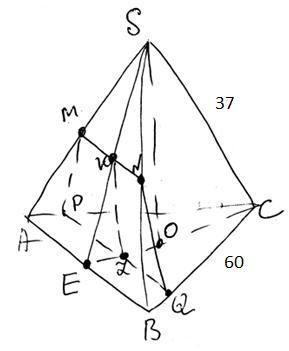
Рассмотрим прямоугольный треугольник SOE, где SO – высота правильной пирамиды. Точка O лежит на пересечении медиан правильного треугольника (в основании пирамиды) и делит их в отношении 2:1, то есть

.

Точка K является серединой отрезка MN, причем  , откуда следует, что  . Так как  , то  . Таким образом, получаем, что  .

б) Расстояние от точки A до плоскости   - это перпендикуляр от точки A до плоскости  , длина которого равна отрезку EZ. Так как  , найдем длину отрезка CE из прямоугольного треугольника ECB по теореме Пифагора:

.

Получаем расстояние

.