У

 чебный элемент
чебный элемент
Тема: «Логические основы обработки информации.» - 9 -
П редмет: «Информатика»
редмет: «Информатика»
Цели:
Изучив данный учебный элемент, Вы узнаете:
о принципах обработки информации компьютером;
логические основы работы компьютера:
основные логические операции;
логические схемы элементов компьютера;
примеры решения задач по данной теме.
Оборудование, материалы и вспомогательные средства:
персональный компьютер;
мультимедиа проектор;
презентация урока;
раздаточный материал.
Сопутствующие учебные элементы и пособия:
Учебник И.Г. Семакин, Т.Ю. Шеина, Л.В. Шестакова – 10 класс
Логические основы обработки информации основаны на Логике
Логика – это наука о формах и способах мышления.
Основные формы мышления
Понятие
Высказывание
Умозаключение
Понятие – это форма мышления, фиксирующая основные, существенные признаки объекта.
Высказывание – это форма мышления, в которой что-либо утверждается или отрицается о свойствах реальных предметов и отношениях между ними. Высказывание может быть либо истинно, либо ложно.
Умозаключение – это форма мышления, с помощью которой из одного или нескольких суждений(посылок) может быть получено новое суждение (заключение
В алгебре высказываний высказывания обозначаются именами логических переменных, которые могут принимать лишь два значения: «истина»(1) и «ложь»(0)
К базовым логическим операциям относятся:
Логическое умножение (конъюнкция) – «И»
Логическое сложение (дизъюнкция) – «ИЛИ»
Логическое отрицание (инверсия) – «НЕ»
Логическое умножение «И» на формальном языке принято обозначать значком «&» либо «^». Пример: высказывание F=A & B
Таблица истинности логического умножения
| A | B | F=A & B |
|
|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Пример. «2*2 =4 И 3*3 =10» по таблице определяем (А = 1), (В = 0), значит F = 0 – данное высказывание ложно
Логическое сложение «ИЛИ» на формальном языке алгебры логики обозначают «+» либо «v»
Пример: высказывание F=A V B
Таблица истинности логического сложения
| А | B | F=A V B |
|
|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
|
|
|
|
Пример: «2*2 = 4 ИЛИ 3*3 = 10» по таблице определяем (А = 1), (В = 0), значит F = 1 – данное высказывание истинно
Логическое отрицание в алгебре логики обозначают Ā
Пример: F = Ā
Таблица истинности логического отрицания
Таблица истинности - Импликация (логическое следование)

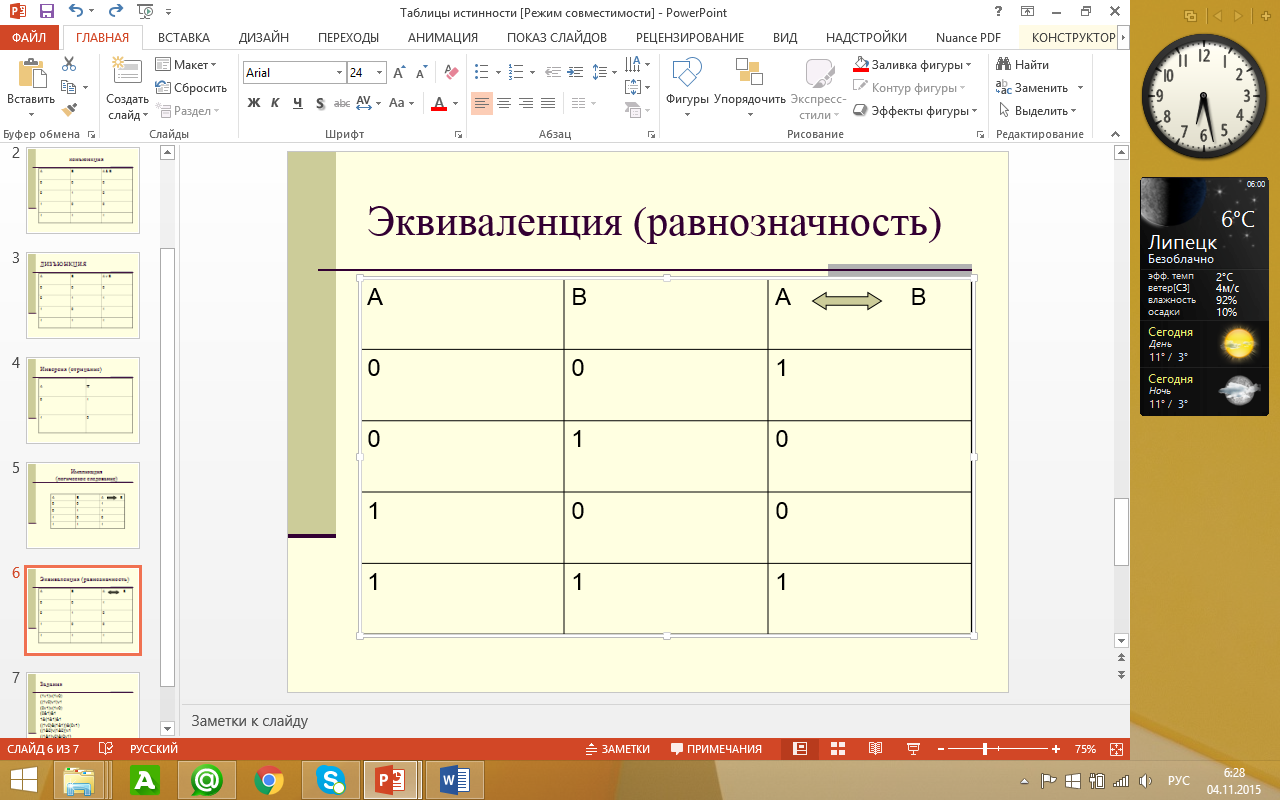
Таблица истинности - Эквивалентность (равнозначность)
Компьютер выполняет арифметические и логические операции при помощи так называемых базовых логических элементов, которые также еще называют вентилями.
Вентиль «И» – конъюнктор
Реализует конъюнкцию
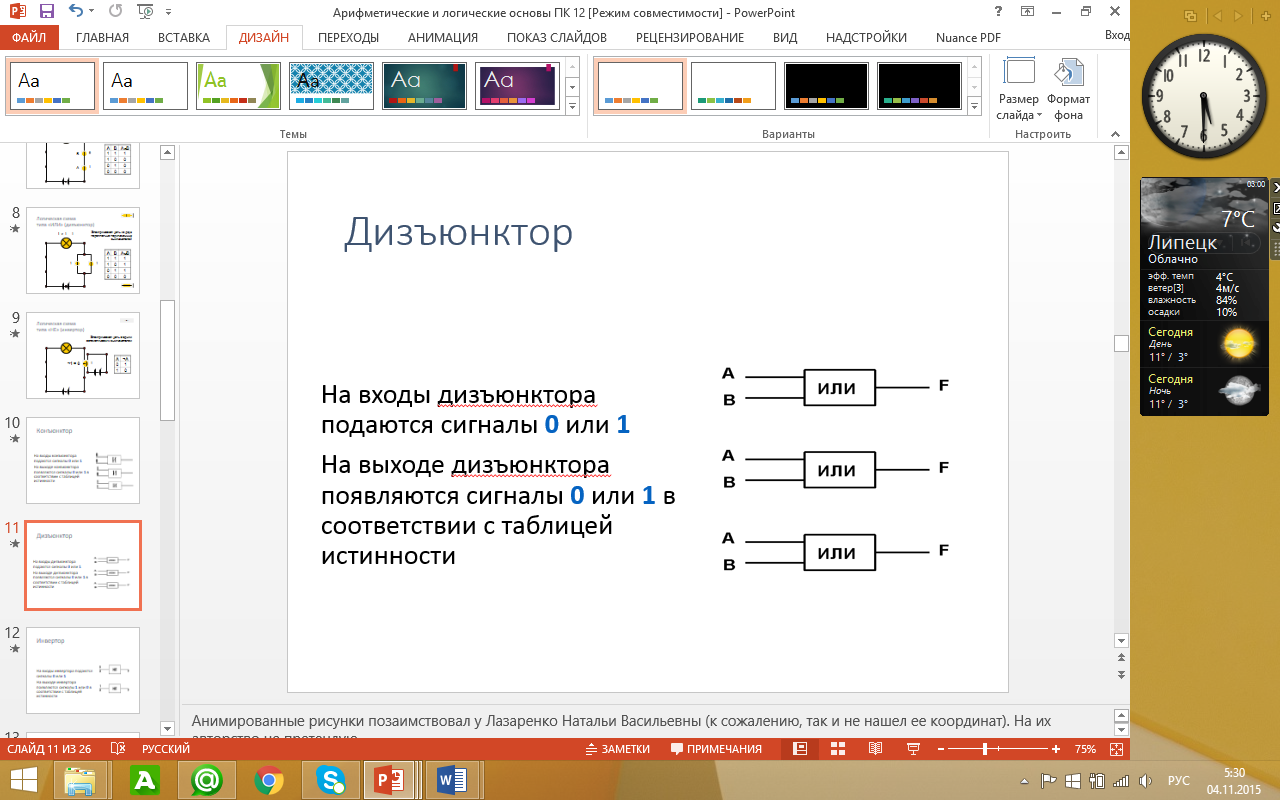
Вентиль «ИЛИ» – дизъюнктор
Реализует дизъюнкцию
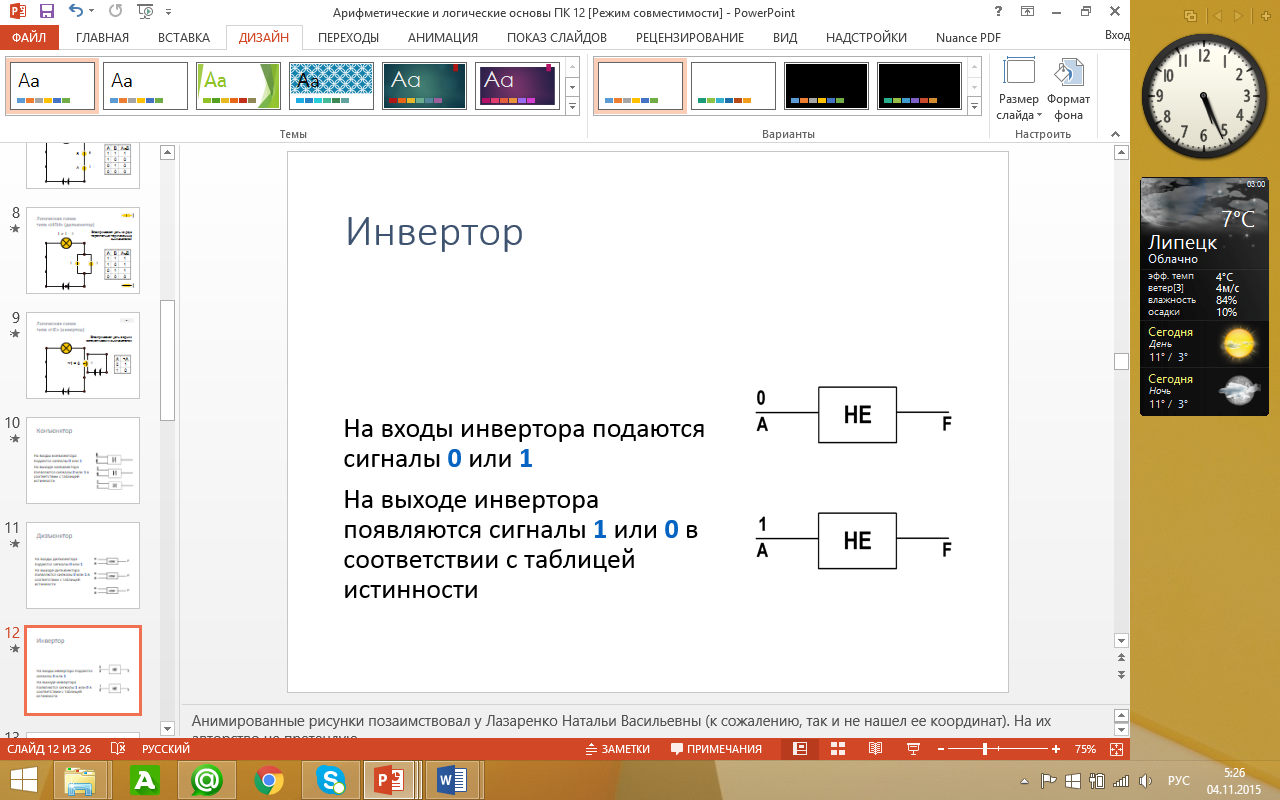
Вентиль «НЕ» – инвертор
Реализует инверсию
Любая логическая операция может быть представлена через конъюнкцию, дизъюнкцию и инверсию.
Любой сколь угодно сложный элемент компьютера может быть сконструирован из элементарных вентилей.
Вентили оперируют с электрическими импульсами:
Н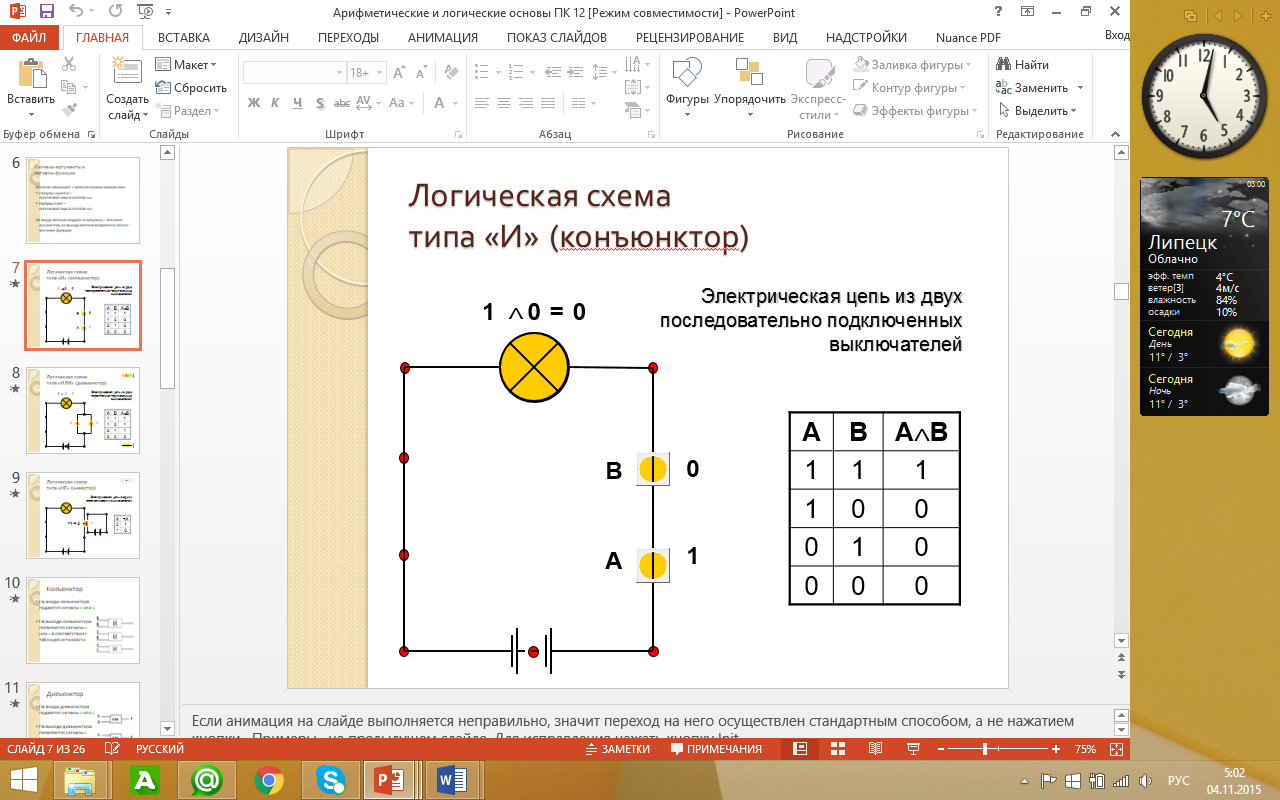 а входы вентиля подаются импульсы – значения аргументов, на выходе вентиля появляется сигнал – значение функции
а входы вентиля подаются импульсы – значения аргументов, на выходе вентиля появляется сигнал – значение функции





Пример.
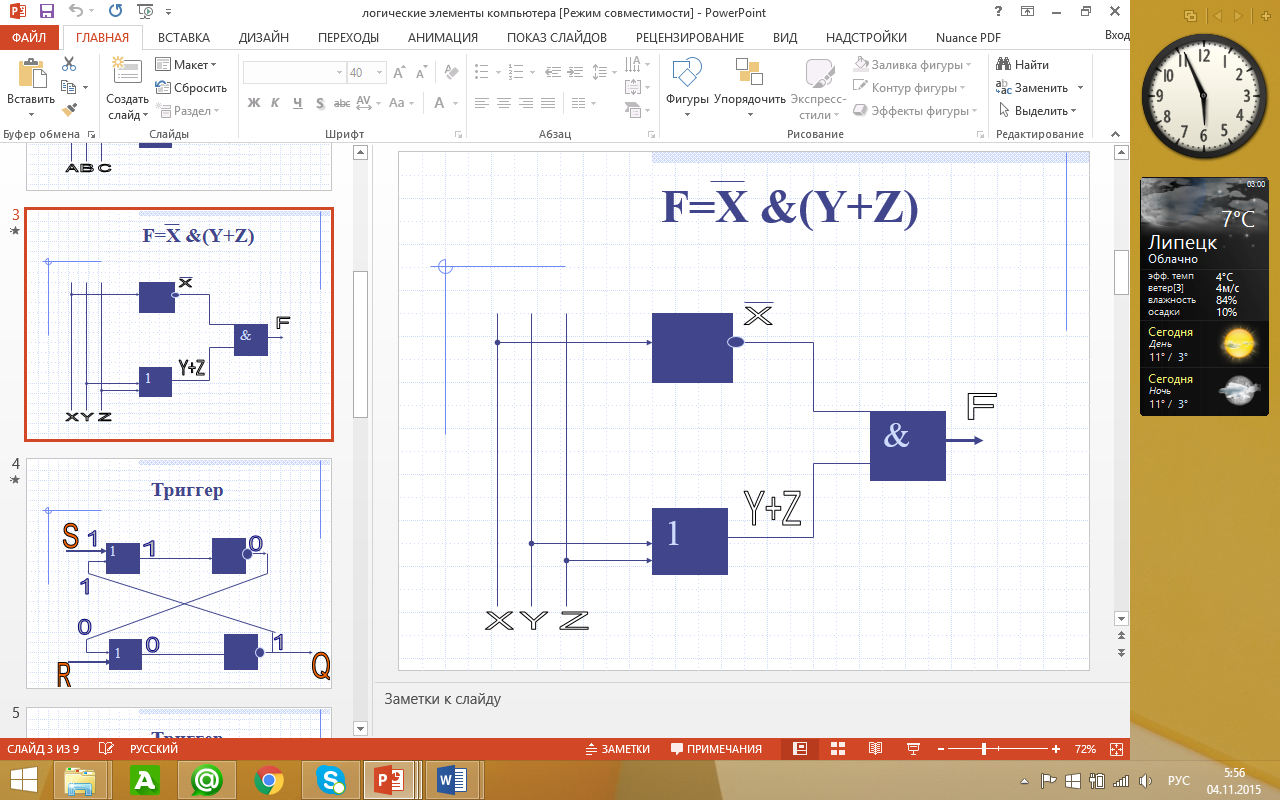
Сумматор двоичных чисел
Все математические действия в компьютере сводятся к сложению двоичных чисел. Основу микропроцессора составляют сумматоры двоичных чисел
Триггер
Важнейшая структурная единица оперативной памяти и регистров процессора. Состоит из двух логических элементов «ИЛИ» и двух логических элементов «НЕ»
Логическая схема триггера

Работа триггера
В обычном состоянии на входы триггера S и R подан сигнал «0» и триггер хранит «0».
При подаче сигнала «1» на вход S триггер принимает значение на выходе Q значение «1»
При подаче сигнала «1» на вход R триггер возвращается в свое исходное состояние – хранит «0».
Построение таблиц истинности логических выражений
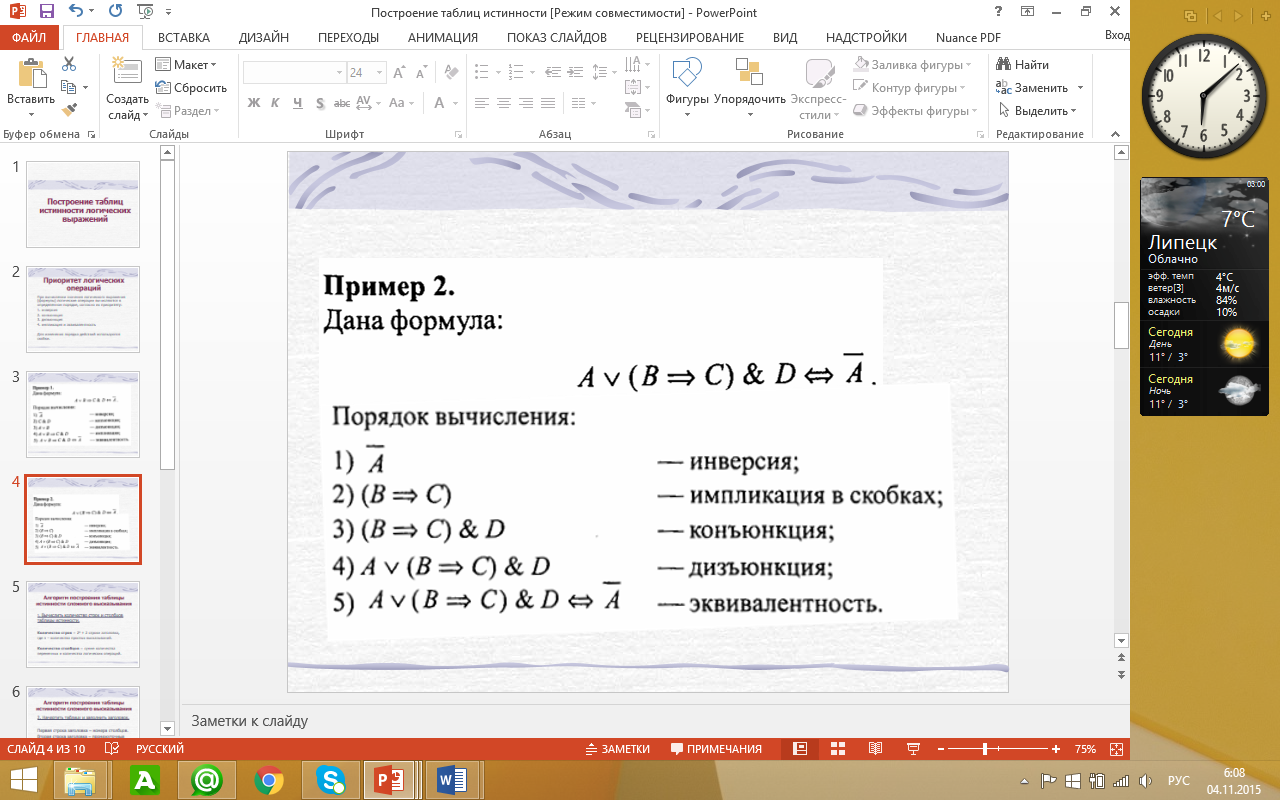
При вычислении значения логического выражения (формулы) логические операции вычисляются в определенном порядке, согласно их приоритету:
инверсия
конъюнкция
дизъюнкция
импликация и эквивалентность
Для изменения порядка действий используются скобки.
Самостоятельная работа
Задание 1
Выполнить логические операции:
(1 v 1) v (1 v )
((1 v 0) v 1) v 1
(0 v 1) v (1 v 0)
(0 & 1) & 1
1 & (1 & 1) & 1
((1 v 0) & (1 & 1)) & (0 v 1)
((1 & 0) v (1 & 0)) v 1
((1 & 1) v 0) & (0 v 1)
((0 & 0) v 0) & (1 v 1)
Задание 2
Построить таблицу истинности для логического выражения:
A & (B v B & C)
Задание 3
Доказать, что логические выражения A & B и A v B равносильны.
Контрольные вопросы
Дать определение науке «Логика».
Назвать логические операции.
Как изображаются логические схемы?
Рассказать о работе триггера.

Иванилова Т.С.
Липецкий политехнический техникум









 чебный элемент
чебный элемент редмет: «Информатика»
редмет: «Информатика»

 а входы вентиля подаются импульсы – значения аргументов, на выходе вентиля появляется сигнал – значение функции
а входы вентиля подаются импульсы – значения аргументов, на выходе вентиля появляется сигнал – значение функции



















