Тема: Логические основы ЭВМ
Даны простые высказывания:
А = {Принтер – устройство ввода информации},
В = {Процессор – устройство обработки информации},
С = {Монитор – устройство хранения информации},
D = {Клавиатура – устройство ввода информации}.
Определите истинность составных высказываний:
а) (АВ) (C D); б) (АВ) (C D);
в) (А В)↔(C D); г)  ↔
↔  .
.
Найдите значения логических выражений:
а) (11) (10); б) ((10) 1) 1;
в) (01) (10); г) (0&1)&1;
д) 1&(1&1)&1; е) ((10)&(1&1))&(01);
ж) ((1&0) (1&0)) 1; з) ((1&1) 0)&(01);
и) ((0&0) 0)&(11).
Составить таблицу истинности:
T=(((AB)B)C)(AC)
W=(((AB)B) C)(AC)
Дан фрагмент таблицы истинности выражения F.
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | F |
| 1 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 0 |
| 0 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
Какое выражение соответствует F?
1) (x2 x1) ¬x3 x4 ¬x5 x6 ¬x7 x8
2) (x2 x1) ¬x3 x4 ¬x5 x6 ¬x7 x8
3) ¬(x2 x1) x3 ¬x4 x5 ¬x6 x7 ¬x8
4) (x2 x1) x3 ¬x4 x5 ¬x6 x7 ¬x8
С х е м а И
Схема И реализует конъюнкцию двух или более логических значений. Условное обозначение на структурных схемах схемы И с двумя входами представлено на рис. 5.1.

Рис. 5.1
Таблица истинности схемы И
| x | y | x . y |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Единица на выходе схемы И будет тогда и только тогда, когда на всех входах будут единицы. Когда хотя бы на одном входе будет ноль, на выходе также будет ноль.
Связь между выходом z этой схемы и входами x и y описывается соотношением: z = x . y
(читается как "x и y"). Операция конъюнкции на структурных схемах обозначается знаком "&" (читается как "амперсэнд"), являющимся сокращенной записью английского слова and.
С х е м а ИЛИ
Схема ИЛИ реализует дизъюнкцию двух или более логических значений. Когда хотя бы на одном входе схемы ИЛИ будет единица, на её выходе также будет единица.
Условное обозначение на структурных схемах схемы ИЛИ с двумя входами представлено на рис. 5.2. Знак "1" на схеме — от устаревшего обозначения дизъюнкции как "=1" (т.е. значение дизъюнкции равно единице, если сумма значений операндов больше или равна 1). Связь между выходом z этой схемы и входами x и y описывается соотношением: z = x v y (читается как "x или y").

Рис. 5.2
Таблица истинности схемы ИЛИ
| x | y | x v y |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
С х е м а НЕ
Схема НЕ (инвертор) реализует операцию отрицания. Связь между входом x этой схемы и выходом z можно записать соотношением z =  , x где
, x где  читается как "не x" или "инверсия х".
читается как "не x" или "инверсия х".
Если на входе схемы 0, то на выходе 1. Когда на входе 1, на выходе 0. Условное обозначение на структурных схемах инвертора — на рисунке 5.3

Рис. 5.3
Таблица истинности схемы НЕ
| x | 
|
| 0 | 1 |
| 1 | 0 |
С х е м а И—НЕ
Схема И—НЕ состоит из элемента И и инвертора и осуществляет отрицание результата схемы И. Связь между выходом z и входами x и y схемы записывают следующим образом:  , где
, где  читается как "инверсия x и y". Условное обозначение на структурных схемах схемы И—НЕ с двумя входами представлено на рисунке 5.4.
читается как "инверсия x и y". Условное обозначение на структурных схемах схемы И—НЕ с двумя входами представлено на рисунке 5.4.

Рис. 5.4
Таблица истинности схемы И—НЕ
| x | y | 
|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
С х е м а ИЛИ—НЕ
Схема ИЛИ—НЕ состоит из элемента ИЛИ и инвертора и осуществляет отрицание результата схемы ИЛИ. Связь между выходом z и входами x и y схемы записывают следующим образом:  , где
, где  , читается как "инверсия x или y ". Условное обозначение на структурных схемах схемы ИЛИ—НЕ с двумя входами представлено на рис. 5.5.
, читается как "инверсия x или y ". Условное обозначение на структурных схемах схемы ИЛИ—НЕ с двумя входами представлено на рис. 5.5.

Рис. 5.5
Таблица истинности схемы ИЛИ—НЕ
| x | y | 
|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
Сигнал, выработанный одним логическим элементом можно подавать на вход другого логического элемента. Это дает возможность образовывать цепочки из отдельных логических элементов. На рисунке 15 показаны примеры таких цепочек.
|  а) а)
|  б) б)
|
Рисунок 15. Цепочка из нескольких логических элементов
На рисунке 15 а) элемент ИЛИ (дизъюнктор) соединен с элементом НЕ (инвертор), а на рисунке 15 б) - элемент И (конъюнктор) с элементом НЕ (инвертор). Каждую такую цепочку будем называть логическим устройством: поскольку она состоит из нескольких элементов.
Цепочку из логических элементов будем называть логическим устройством. Схемы, соответствующие таким устройствам, называют функциональными.
На рисунке 16 приведен пример более сложной функциональной схемы.
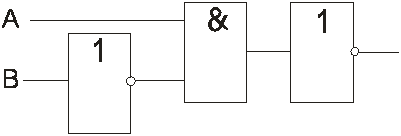
Рисунок 16. Сложная функциональная схема
Построить логическую схему ØХ& ØY


 . Вычерчиваем по логическому выражению функциональную схему.
. Вычерчиваем по логическому выражению функциональную схему.
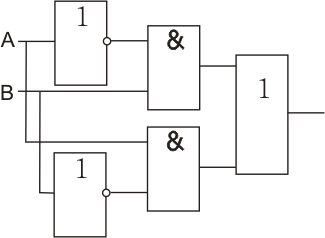
Рисунок 17. Функциональная схема логической функции  .
.

-(-А+-В) 
Домашнее задание:
Постройте логическую схему, соответствующую логическому выражению F=А&Вv (ВvА). Вычислить значения выражения для А=1,В=0.
Переменных две: А и В;
Логических операций три: & и две v; А&Вv (Вv А).
Схему строим слева направо в соответствии с порядком логических операций:












 а)
а) б)
б)













