Тема: Логические выражения и таблицы истинности.
Цели: - научить учащихся составлять таблицы истинности логических функций;
- формирование у учащихся компьютерной грамотности.
Ход урока.
Организационный момент.
Постановка цели.
Анализ практической работы.
Объяснение нового материала.
Логические выражения.
Каждое составное высказывание можно выразить в виде формулы (логического выражения), в которую входят логические переменные, обозначающие высказывания, и знаки логических операций, обозначающие логические функции.
Для записи составного высказывания в виде логического выражения на формальном языке (языке алгебры логики) в составном высказывании нужно выделить простые высказывания и логические связи между ними.
Например, пусть дано составное высказывание:
«(2 · 2 = 5 или 2 · 2 = 4) и (2 · 2 ≠ 5 или 2 · 2 ≠ 4)».
Оно содержит два простых высказывания:
А = «2 · 2 = 5» - ложно (0), В = «2 · 2 = 4» - истинно (1).
Тогда составное высказывание можно записать так:
«(А или В) и (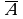 или
или 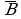 )».
)».
В форме логического высказывания:
F = (А 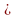 В) & (
В) & (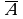
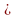
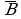 ) = (0
) = (0 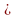 1) & (1
1) & (1 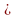 0) = 1 & 1 = 1.
0) = 1 & 1 = 1.
Таблицы истинности.
Для каждого составного высказывания можно построить таблицу истинности, которая определяет его истинность или ложность при всех возможных комбинациях исходных значений простых высказываний (логических переменных).
Для этого необходимо:
определить количество строк в таблице истинности: количество строк = 2n, где n – количество логических переменных (в нашем случае две переменные, значит количество строк 22 = 4).
определить количество столбцов в таблице истинности, которое равно количеству логических переменных плюс количество логических операций (в нашем случае две переменные плюс пять операций = 7).
построить количество строк и столбцов, обозначить столбцы и внести в таблицу возможные наборы значений исходных логических переменных.
заполнить таблицу истинности по столбцам, выполняя базовые логические операции в необходимой последовательности и в соответствии с их таблицами истинности, учитывая порядок действий (инверсия, конъюнкция, дизъюнкция).
| А | В | А 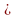 В В | 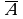
| 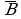
| 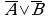
| 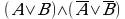
|
| 0 | 0 | 0 | 1 | 1 | 1 | 0 |
| 0 | 1 | 1 | 1 | 0 | 1 | 1 |
| 1 | 0 | 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 1 | 0 | 0 | 0 | 0 |
Наборы входных переменных, во избежание ошибок, рекомендуется перечислять следующим образом:
разделить колонку значений первой переменной пополам и заполнить верхнюю часть колонки нулями, а нижнюю единицами;
разделить колонку значений второй переменной на четыре части и заполнить каждую четверть чередующимися группами нулей и единиц, начиная с группы нулей;
продолжать деление колонок значений последующих переменных на 8, 16 и так далее частей и заполнение их группами нулей и единиц до тех пор, пока группы нулей и единиц не будут состоять из одного символа.
Например, для формулы 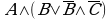 построить таблицу истинности.
построить таблицу истинности.
| 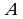
| 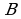
| 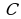
| 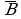
| 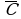
| 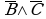
| 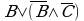
| 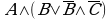
|
| 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 |
| 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 0 | 0 | 1 | 0 |
| 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 |
| 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 |
Равносильные логические выражения.
Логические выражения, у которых последние столбцы таблиц истинности совпадают, называются равносильными ( = ).
Например, докажем, что логические выражения 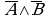 и
и 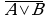 равносильны.
равносильны.
| 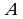
| 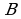
| 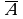
| 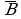
| 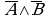
|
| 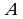
| 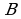
| 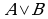
| 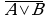
|
| 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 1 |
| 0 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 0 |
Значения в последних столбцах таблиц истинности совпадают, следовательно, логические выражения равносильны: 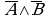 =
= 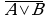 .
.
Подвести итоги. Выставить оценки. Д/З: стр. 129 – 132.







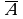 или
или 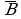 )».
)».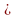 В) & (
В) & (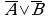
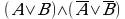
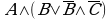 построить таблицу истинности.
построить таблицу истинности.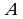
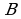
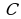
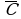
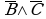
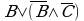
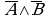 и
и 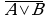 равносильны.
равносильны.