К началу учебного года! Готовые материалы для учителей на каждый урок со скидкой от 30%

СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ

Благодаря готовым учебным материалам для работы в классе и дистанционно

Выбрать материалы

Скидки до 50 % на комплекты
только до

Готовые ключевые этапы урока всегда будут у вас под рукой

Организационный момент

Проверка знаний

Объяснение материала

Закрепление изученного

Итоги урока

Логические задачи для начальной школы

Категория: Начальные классы

29.07.2024 16:04

Образовательный стандарт нового поколения ставит перед начальным образованием новые цели. Теперь в начальной школе ребёнка должны научить не только читать, считать и писать, ему должны привить две группы новых умений. Речь идёт, во-первых, об универсальных учебных действиях, составляющих умения учиться: навыках решения творческих задач и навыка поиска, анализа и интерпретации информации. Во-вторых, речь идёт о формировании у детей мотивации к обучению, саморазвитию, самопознанию. Учителю, который до этого занимался с ребятами просто математикой как таковой, теперь придётся на знакомом ему материале решать ещё и новые нестандартные задачи. Уже в начальной школе дети должны овладеть элементами логических действий (сравнения, классификации, обобщения, анализа и др.). Поэтому одной из важнейших задач, стоящих перед учителем начальных классов, является развитие самостоятельной логики мышления, которая позволила бы детям строить умозаключения, приводить доказательства, высказывания, логически связанные между собой, делать выводы, обосновывая свои суждения, и, в конечном итоге, самостоятельно приобретать знания. Математика именно тот предмет, где можно в большой степени это реализовывать.

Просмотр содержимого документа
«Логические задачи для начальной школы»

и 2 клоуна, 3 обезьяны, 5 собачек, 2 кошки, 4 кролика и

дрессировщица. Сколько животных на арене?

№ 21. Продолжи последовательность чисел

СОДЕРЖАНИЕ

Список творческой группы…………………………………………….2

План работы……………………………………………………….…….3

Пояснительная записка………………………………………………....4

Логические задания для 1 класса…………………………………..…. 6

Логические задания для 2 класса………………………………….…. 11

Логические задания для 3 класса………………………………….… 18

Логические задания для 4 класса………………………………….… 20

Олимпиадные логические задания 3-4 класс………………………. 26

Использованная литература………………………………………… 31

Состав творческой группы

№ п/п	ФИО учителя	Категория	Название МОУ
1.	Кобзарь Ирина Юрьевна (руководитель группы)	высшая квалификационная категория	МБОУ «ШКОЛА № 106 ГОРОДА ДОНЕЦКА»
2.	Кокарева Юлия Сергеевна	вторая квалификационная категория	МБОУ «Александровская школа Марьинского района»
3.	Самофалова Наталья Викторовна	специалист	МБОУ «ШКОЛА № 110 ГОРОДА ДОНЕЦКА»
4.	Шалимова Инна Александровна	вторая квалификационная категория	МБОУ «ШКОЛА № 101 ИМ. УДОДОВА ГОРОДА ДОНЕЦКА»

План работы

районной творческой группы учителей 2-х классов по теме:

«Логические задания по математике в начальной школе»

№	Мероприятия	Дата	Ответственные
1.	Вступительное заседание творческой группы. Обсуждение темы. Составление плана работы. Распределение заданий между членами группы.	Август 2023г.	Кобзарь И.Ю.
2.	Изучение проблемы, подбор материалов соответственно заданной теме, рекомендаций.	Октябрь-ноябрь 2023г.	Кобзарь И.Ю. учителя
3.	Практическое занятие. Рассмотрение подготовленного материала членами группы.	Январь 2024г.	Учителя
4.	Итоговое занятие. Анализ работы творческой группы.	Март 2024г.	Все

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА

Логика – наука о законах и формах правильного мышления. Она изучает формы рассуждений, отвлекаясь от конкретного содержания, устанавливает, что из чего следует, ищет ответ на вопрос: как мы рассуждаем? Основоположником логики как науки является древнегреческий философ и ученый Аристотель. Он впервые разработал теорию логического вывода.

Начальное образование призвано заложить базовые основы общего умственного развития детей, которые создали бы условия для воспитания самостоятельно мыслящего, критично оценивающего свои действия человека. В младшем школьном возрасте дети располагают значительными резервами развития, именно этот возраст является продуктивным в развитии логического мышления: дети включаются в новые для них виды деятельности и системы межличностных отношений, требующие от них наличия новых психологических качеств.

В первом классе система заданий предусматривает несколько групп систематически выстроенных задач и заданий, направленных преимущественно на выделение, прослеживание, распределение и изменение различных признаков и характеристик объектов.

Во втором классе продолжается работа по развитию умения производить простые логические действия. Задания на классификацию усложнились: они неразрывно связаны с развитием у детей способности строить цепочки логических рассуждений.

В 3-4-х классах школьники должны научиться анализировать связи между предметами и явлениями (часть и целое, противоположность, причина и следствие, наличие тех или иных функциональных отношений и др.).

К окончанию начальной школы у ребенка должны быть сформулированы такие операции логического мышления как обобщение, классификация, анализ и синтез. Учащийся должен научиться таким элементам анализа как выявление и других связей между понятиями: противоположность, наличие тех или иных функциональных отношений, часть и целое и т.д.

Таким образом, формирование логического мышления – это важная составная часть педагогического процесса. Помочь в полной мере проявить свои способности, развить инициативу, самостоятельность, творческий потенциал - одна из основных задач современной школы. Успешная реализация этой задачи во многом зависит от сформированности у учащихся логического мышления.Использование учителем начальной школы этих форм и методов развития логического мышления на уроках математики является не только желательным, но даже необходимым элементом обучения математике.

Систематическое использование на уроках математики и внеурочных занятиях специальных упражнений и заданий, направленных на развитие логического мышления, расширяют кругозор младших школьников, позволяет более уверенно ориентироваться в простейших закономерностях окружающей их действительности. Нужно помнить, что последовательность и систематичность в работе с детьми – залог успешного решения поставленных задач.

Задания для 1 класса с ответами.

№ 1. Лестница состоит из 9 ступенек. Какая ступенька находится на середине?

№ 2. У животного 3 правые ноги, 3 левые ноги, 3 ноги сзади, 3 ноги спереди. Сколько всего ног у животного?

№ 3. Три мальчика готовили елочные игрушки к Новому году. Втроем они работали 3 часа. Сколько часов работал каждый из них?

№ 4. Сумма трех нечетных чисел равна 15. Напиши эти числа, если известно, что слагаемые не равны между собой.

№ 5. Поставь знаки «+» или «-», чтобы получилось верное равенство:
8*5*4*3 = 10 10*2*7*4 = 1.

№ 6. Из-под ворот видно 12 щенячьих лап. Сколько щенят во дворе?

№ 7. Сколько получим, если добавим к самому большому двузначному числу 1?

№ 8. «Мой хвост, — сказала кошка, — имеет длину 10 см и еще половину моего хвоста». Какова длина хвоста кошки?

№ 9. Гриша, Артур, Саша и Вадим играли в шашки. Каждый сыграл с каждым по одной партии. Сколько всего партий сыграно?

№ 10. Лист бумаги согнули пополам, потом еще пополам и еще пополам. Затем лист разрезали по линиям сгиба. Сколько получилось листочков?

№ 11. Две дыни весят столько же, сколько один арбуз. Что тяжелее: 5 дынь или 3 арбуза?

№ 12. В ателье по пошиву женской одежды от рулона материи в 100 м ежедневно, начиная с 1 мая, отрезали по 10 м. Когда был отрезан последний кусок?

№ 13. На одном дереве сидело 10 ворон. Мимо проходил охотник, выстрелил и убил 7 ворон. Сколько ворон осталось на дереве?

№ 14. В корзине лежат груши. Известно, что их можно разделить поровну между 2 или 3 детьми. Сколько груш в корзине, если их меньше 10?

№ 15. Миша задумал число. Если из него вычесть 7 и прибавить 2, то получится 5. Какое число задумал Миша?

№ 16. У Веры было 50 рублей. Какие игрушки она может купить?
1) Куклу за 37 рублей и пенал за 15 рублей.
2) Мяч за 42 рубля и скакалку за 7 рублей.
3) Альбом за 35 рублей и зеленое ведерко за 17 рублей.
4) Набор карандашей за 22 рубля и детский утюг за 30 рублей.

№ 17. 8 + 2 меньше, чем Я,
7 + 5 больше, чем Я.
Кто Я?

№ 18. Сколько здесь чисел, которые меньше 7?
2, 5, 8, 3, 6, 9, 1, 4, 7.

№ 19. Гриша стоит в очереди за квасом третьим, за ним еще четверо. Сколько их всего?

№ 20. На цирковой арене выступали 2 клоуна, 3 обезьяны, 5 собачек, 2 кошки, 4 кролика и дрессировщица. Сколько животных на арене?

№ 21. Продолжи последовательность чисел
11, 8, 5, ... .

№ 22. В первом и третьем классах учится одинаковое количество отличников. Во втором классе отличников в 2 раза больше, чем в первом классе. В каком классе больше всего отличников?

№ 23. Таня поднялась с первого на шестой этаж. Чтобы подняться на один этаж, надо пройти 10 ступенек. Сколько всего ступенек прошла Таня?

№ 24. Какое число меньше 17 на 3?

№ 25. У Вани — три сестры, а у Пети — один брат. Сколько родителей у детей?

№ 26. Шли два отца и два сына, нашли три яблока. Стали делить — всем по одному досталось. Как это могло быть?

№ 27. У квадратного стола отпилили один угол по прямой линии. Столько стало углов у стола?

№ 28. Один оборот вокруг Земли спутник делает за 1 ч 40 мин, а другой — за 100 мин. Как такое может быть?

№ 29. В одной корзине Настя несла 1 кг железа, а в другой столько же ваты. Что было тяжелее нести?

№ 30. У него есть четыре, но если их все отрезать, то у него станет целых восемь. О чем идет речь?

№ 31. Если в 12 часов ночи идет дождь, то можно ли ожидать, что через 72 часа будет солнечная погода?

№ 32. Позавчера Артуру было 9 лет. В следующем году ему исполнится 12 лет. Как такое возможно?

№ 33. В классе 12 парт. Покрасили 5 парт. Сколько парт стало в классе?

№ 34. Термометр показывает 30 °С. Сколько градусов покажут два таких термометра?

№ 35. На дереве сидели 4 воробья, одного из них съела кошка. Сколько воробьев осталось на дереве?

№ 36. Как написать «девятнадцать», а затем, убрав единицу, получить «двадцать»?

№ 37. Сколько концов у двух палок? У трех с половиной?

№ 38. На подносе лежали 10 пирожков. 10 мальчиков взяли по пирожку. Но на подносе остался один пирожок. Как такое возможно?

№ 39. Собрались как-то ребята на пикник, всего 7 человек. Смотрят, а вместо 7 яблок они взяли 6. Как разделить яблоки поровну между всеми, чтоб никому не было обидно? Ни резать, ни ломать их нельзя.

№ 40. Три курицы несут три яйца за 3 дня. Сколько яиц снесут 12 куриц за 12 дней?

Ответы к задачам:

№1. Ответ: Пятая.

№ 2. Ответ: 8 ног.

№ 3. Ответ: 3 часа.

№ 4. Решение. 3 + 5 + 7 = (3 + 7) + 5 = = 10 + 5 = 15.

№ 5. Решение.
8-5 + 4 + 3 = 10.
10 + 2- 7- 4 = 1.

№ 6. Ответ: трое щенят.

№ 7. Ответ: 100.

№ 8.
Ответ: 20 см.

№ 9. Решение.
Г → А
↓ Х ↓
С → В
Ответ: Всего сыграно 6 партий.

№ 10. Ответ: 8 листочков.

№ 11. Решение.
Если один арбуз весит, как две дыни, то три арбуза будут весить столько же, сколько шесть дынь. Значит, три арбуза тяжелее пяти дынь.
Ответ: 3 арбуза.

№ 12. Решение.
1 мая — 10 м материи, 2 мая — 20 м, 3 мая — 30 м, 4 мая — 40 м, 5 мая — 50 м,
6 мая — 60 м, 7 мая — 70 м, 8 мая — 80 м,
9 мая — 90 м. Значит, последний кусок материи
отрезан 9 мая.
Ответ: 9 мая.

№ 13. Ответ: Ни одной, все улетели.

№ 14. Ответ: 6 груш.

№ 15. Решение.
Начнем с конца: 5 - 2 + 7 = 10.
Ответ: Миша задумал число 10.

№ 16. Решение.
Вера может купить мяч за 42 рубля и скакалку за 7 рублей:
42 + 7 = 49 (рублей).
Ответ: Мяч и скакалку.

№ 17. Решение.
8 + 2 = 10
7 + 5 = 12, 10 Ответ: 11.

№ 18. Ответ: Всего 6 чисел.

№ 19.
Решение.
Впереди Гриши двое, после него еще четверо, кроме того он сам. Всего будет 2 + 4 + 1 = = 7 человек.
Ответ: 7.

№ 20. Решение.
3 обезьяны, 5 собачек, 2 кошки, 4 кролика. Всего животных:
3 + 5 + 2 + 4 = 14.
Ответ: 14 животных.

№ 21. Ответ: 11, 8, 5, 2.

№ 22. Ответ: Во 2-м классе.

№ 23. Решение.
10 + 10 + 10 + 10 + 10 = 50 ступенек.
Ответ: Таня прошла 50 ступенек.

№ 24. Ответ: 14.

№ 25. Решение.
У Вани и его сестер одна мама и один папа.
У Пети и его брата тоже одна мама и один
папа. Вместе у детей 4 родителя.
Ответ: У детей 4 родителя.

№ 26. Ответ: Это были дед, отец и сын.

№ 27.
Ответ: Пять.

№ 28. Решение.
1 ч 40 мин = 60 мин + 40 мин = 100 мин. Ответ: Да, может, так как 1 ч 40 мин = 100 мин.

№ 29. Ответ: Одинаково.

№ 30. Ответ: Об углах четырехугольника.

№ 31. Ответ: Нет, так как через 72 часа опять будет полночь.

№ 32. Решение.
Если нынешний день 1 января, а день рождения у Артура 31 декабря. Позавчера (30 декабря) ему было еще 9 лет, вчера (31 декабря) исполнилось 10 лет, в нынешнем году исполнится 11 лет, а в следующем — 12.

№ 33. Ответ: 12 парт.

№ 34. Ответ: 30 °С.

№ 35. Решение.
Ни одного воробья не осталось, оставшиеся в живых разлетелись.
Ответ:
Ни одного.

№ 36. Ответ: XIX.

№ 37. Ответ: У двух палок — 4 конца, у трех с половиной 6 + 2 = 8 концов.

№ 38. Ответ: Последний из мальчиков взял пирожок вместе с подносом.

№ 39. Ответ: Нужно сварить компот.

№ 40. Решение.
Можно машинально ответить, что 12 куриц за 12 дней снесут 12 яиц. Однако это вовсе не так. Если три курицы за 3 дня несут 3 яйца, то одна курица за те же 3 дня снесет одно яйцо. Значит, за 12 дней она снесет: 12 : 3 = 4 яйца. А если куриц 12, то за 12 дней они снесут: 12 • 4 = 48 яиц.
Ответ: 48 яиц.

З адания для 2 класса с ответами и решением

Задача 1.
Имеется перекрёсток двух дорог. Вдоль каждой из дорог, по одну сторону на этом перекрёстке надо посадить по 11 деревьев. Каково наименьшее количество деревьев, которые можно посадить, выполняя это задание?
(Наименьшее количество деревьев 21)

Задача 2.
Тетрадь дешевле ручки, но дороже карандаша. Что дешевле?
( Дешевле карандаш)

Задача 3.
Какие три числа, если их сложить или перемножить, дают один и тот же результат?
( 1, 2, 3 (1 + 2 + 3 = 6, 1 * 2 * 3 = 6)

Задача 4.
В семье четверо детей, им 5, 8, 13 и 15 лет, а зовут их Таня, Юра, Света и Лена. Сколько лет каждому из них, если одна девочка ходит в детский сад, Таня старше, чем Юра, а сумма лет Тани и Светы делится на 3?
(Тане не может быть 15, т.к. 15 + 5 = 20 не кратно 3
Юре не может быть 5, т.к. младший из детей ходит в сад, и по условию это девочка.
Значит Тане 13. А Юре 8.
Свете не может быть 15, т.к. 15 + 13 = 28, не кратно 3. Значит Свете 5.
Остается сказать, что Лене 15.
Ответ : Свете 5 лет, Юре 8 лет, Тане 13 лет, Лене 15 лет).

Задача 5.
У бабушки два внука : Коля и маленький Олег. Бабушка купила им 16 конфет и сказала Коле, чтобы он дал Олегу на 2 конфеты больше, чем взял себе. Как Коля должен разделить конфеты?
(Решение :
16 - 2 = 14 конфет
14 : 2 = 7 конфет у каждого мальчика
7 + 2 = 9 конфет у Олега
Ответ : у Олега 9 конфет, 7 конфет у Коли)

Задача 6.
На весах, которые находятся в равновесии, на одной чашке лежит 1 морковка и 2 одинаковые редиски. На другой чашке – 2 такие же морковки и 1 такая же редиска. Что легче : морковка или редиска?
(Убираем с весов по одной редиске. На одной чаше останутся 1 морковь и 1 редиска, на другой чаше 2 морковки. Если морковки одинаковые, то с каждой чаш убираем по морковке. Получается вес редиски на одной чаше равен весу морковки.
Ответ : Масса морковки равна массе редиски)

Задача 7.
Отца одного гражданина зовут Николай Петрович, а сына – Алексей Владимирович. Как зовут гражданина?
( Владимир Николаевич)

Задача 8.
Ваня живет выше Пети, но ниже Сени, а Коля живет ниже Пети. На каком этаже четырёхэтажного дома живёт каждый из них?
1 этаж – Сеня
2 этаж – Ваня
3 этаж – Петя
4 этаж – Коля

Задача 9.

Двое подошли к реке. Лодка, на которой можно переправиться, вмещает одного человека. И все же, без посторонней помощи, они переправились на этой лодке. Как

им это удалось?
( Двое были на разных берегах реки. Сначала переправился один, а потом другой)

Задача 10.
Полтора лимона стоят полтора рубля. Сколько стоят десять лимонов?
(Так как поллимона стоят пол рубля, то целый лимон стоит 1 рубль, а 10 лимонов – 10 рублей. Ответ : 10 рублей)

Задача 11.
За книгу заплатили один рубль и ещё половину стоимости книги. Сколько стоит книга?
(Так как 1 рубль – это половина стоимости книги, то вторая половина стоимости еще 1 рубль. Итого книга стоит 2 рубля.)

Задача 12.
Стоят двое. Один смотрит на юг, другой на север.
Могут ли они увидеть друг друга, не поворачивая головы, не употребляя зеркал или каких – либо приспособлений?
(Они стоят лицом к лицу)

Задача 13.
Каждую минуту от бревна отпиливают метровый кусок. Во сколько минут распилят на такие куски бревно длиной 6 метров?
( Количество распилов на один меньше, количества полученных кусков. Например, чтобы получить два куска, надо сделать всего один распил. Бревно распилят за 5 минут)

Задача 14.
Два друга – Федя и Костя – получили в школе двойку и тройку.
Федины родители обычно ругают сына за тройки, а привыкшие к тройкам Костины родители ругают его только за двойки. Кому попадет на этот раз, если известно, что Федя не получил тройку?
(Федя – двойку, Костя – тройку).

Задача 15.
Даша и Маша получили в школе пятёрки : одна – по математике, другая – по чтению. По какому предмету получила пятёрку Даша, если Маша получила эту оценку не по математике?
( Маша по чтению, Даша по математике).

Задача 16.
В школьном буфете Наташа, Яна и Алёна покупали пирожные – бисквитное с вареньем, бисквитное с кремом и трубочку с кремом. Кто что купил, если каждая девочка съела по одному пирожному, Яна и Алёна любят пирожные с кремом, а Наташа и Алёна купили себе по бисквитному пирожному?
(Алена – бисквитное с кремом, Яна – трубочку с кремом, Наташа – бисквитное с вареньем).

Задача 17.
Бегемот тяжелее носорога, а носорог тяжелее быка. Кто из этих друзей самый лёгкий?
(Зебра)

Задача 18.
Вите, Пете и Андрею подарили по видеокассете : одну – с комедией, другую с веселыми мультфильмами, а третью с фантастическим фильмом.
Кто что получил в подарок, если известно, что Петя и Витя не любят смотреть мультфильмы, а Андрей и Петя в процессе просмотра хохотали до упаду?
(Вите – фантастический фильм, Пете – комедию, Андрею – мультфильмы).

Задача 19
У трёх подружек – Вики, Ани и Лены – очень красивые куртки – синяя и красная с капюшонами и синяя без капюшона. У кого какая куртка, если Аня и Лена ходят с капюшонами, а у Ани и Вики куртки синего цвета?
(У Вики – синяя, У Ани – синяя с капюшоном, У Лены – красная с капюшоном).

Задача 20.
Три девочки – Таня, Катя и Марина – занимаются в трёх различных кружках – вышивки, танцев и хорового пения. Катя не знакома с девочкой занимающейся танцами. Таня часто ходит в гости к девочке, занимающейся вышивкой. Подружка Кати –Марина, хочет в следующем году добавить к своим увлечениям занятия пением.
Кто из девочек чем занимается?
(Катя – пение, Таня – танцевальный, Марина – вышивку).

Задача 21.
Трое друзей – Игорь, Андрей и Владимир – имеют собак – овчарку, пуделя и добермана.
Игорь живет в одном подъезде с владельцем пуделя.
Доберман, выходя вечером гулять со своим хозяином, всегда очень радуется, встречая Владимира с его собакой, но не переваривает пуделя и всегда злобно облаивает его при встрече.
У кого из мальчиков какая собака?
(У Игоря – доберман, У Владимира – овчарка, У Андрея – пудель).

Задача 22.

В море плавало 9 пароходов. 2 парохода пристали к пристани. Сколько пароходов в море? (9).

Задача 23.

Неожиданно пошел сильный дождь. Но Таня, Саша, Лена не промокли. Почему? (Они наблюдали из окна; у них были плащи, зонты).

Задача 24.

В реке купались дети. Они постоянно ныряли в воду и невозможно их было пересчитать. На берегу были разбросаны кеды, всего 12 штук. Сколько детей купалось в реке? (6).

Задача 25.

Какой знак нужно поставить между 4-мя и 5-ю, чтобы результат оказался больше 4-х и меньше 5-ти? (Запятую)

Задача 26.

Брату и сестре вместе 10 лет. Сколько лет им будет вместе через пять лет? (20 лет)

Задача 27.

По улице шли два отца и два сына, да дедушка с внуком. Сколько всего человек шло по улице? (3 человека)

Задача 28.

Если один петух закукарекает, то человек проснётся. Сколько петухов должны закукарекать, чтобы проснулись три человека? (Один петух)

Задача 29.

На сколько больше наименьшее двузначное число, чем наибольшее однозначное? (На 1)

Задача 30

В автобусе ехало7 человек. На первой остановке вышло 3 пассажира, а село 12. На следующей — вышли 9 человек, зашли 5. Далее — вышли 7, зашли 8. Сколько было остановок? (3 остановки)

Задача 31.

На уроке физкультуры дети выстроились в одну шеренгу с интервалом 1 м. Шеренга растянулась на 20 м. Сколько детей было на уроке? (21 ученик).

Задача 32.

Карина гуляла и видела у реки 4 уток, 2 гусей, жука, 4 бабочки и соседскую собаку. Сколько птиц видела Карина? (6 птиц)

Задачи со спичками (палочками)

Задача 1.

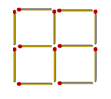
На рисунке можно увидеть 5 квадратов (4 маленьких и 1 большой). Уберите как можно меньше спичек, чтобы осталось ровно 3 одинаковых квадрата.

Ответ: убрать надо 2 спички:

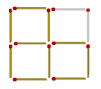
Задача 2.

На рисунке вы видите выложенное из спичек верное равенство. Переложите в нём одну спичку так, чтобы получилось новое верное равенство.

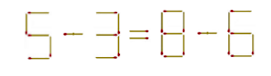
Ответ:

6 - 3 = 9 - 6

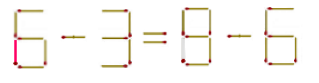
Задача 3.

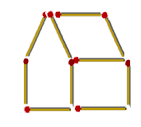
На рисунке сверху изображён домик. Переложив 2 спички, поверните домик в другую сторону.

Ответ:

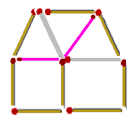
Задача 4. Семь квадратов

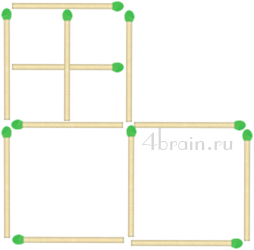
Переложите 2 спички так, чтобы образовать 7 квадратов.

Ответ. Чтобы решить эту достаточно сложную задачу нужно думать нешаблонно. Берем 2 любые спички, образующие угол самого большого внешнего квадрата и кладем их крест-накрест друг на друга в один из маленьких квадратов. Так мы получаем 3 квадрата 1 на 1 спичку и 4 квадрата со сторонами длиной в половину спички.

Задача 5.Оставить 1 треугольник

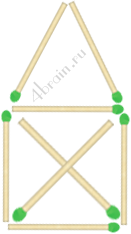
Передвиньте 1 спичку так, чтобы вместо 9 треугольников остался только один.

Решение. Эта головоломка не разгадывается стандартным способом. Для решения поставленной задачи нужно немного исхитриться. Нам нужно избавиться от креста в середине. Берем нижнюю спичку креста, так чтобы она подняла и верхнюю одновременно. Поворачиваем крест на 45 градусов, так чтобы он образовывал в центре домика не треугольники, а квадраты.

Задания для

3 класса

с ответами

№1. В болоте жила – была лягушка Квакушка и ее мама Кваквакушка. На обед Кваквакушка съедала 16 комаров, а Квакушка на 7 меньше, на ужин 15 комаров, а Квакушка на 5 меньше. Сколько комаров нужно лягушкам в день, если они не завтракают.

№2. Мышка- норушка и 2 лягушки- квакушки весят столько же, сколько 2 мышки – норушки и одна лягушка- квакушка. Кто тяжелей: мышка или лягушка?

№3. Курочка Ряба, снесла несколько золотых яиц. Дед с бабой стали их делить. Дед говорит: «Если мы возьмем по 3 яичка, то одно останется». А баба ответила: «Если захотим по 4, то одного не хватит». Пришла внучка и говорит: «У нас 8 яиц». Права ли внучка? Сколько яиц, снесла курочка Ряба?

№4. При постройке забора на квадратном участке в деревне Простоквашино пес Шарик, кот Матроскин и галчонок Хватайка вкапывали столбики. С каждой стороны участка нужно вкопать по 6 столбиков. Сколько столбиков понадобилось коту Матроскину, Шарику и Хватайке для постройки забора?

№5. Шнур 12 метров разрезали на 3 равные по длине части. Сколько разрезов пришлось для этого сделать?

№6. У Незнайки было пять целых груш, шесть половинок да восемь четвертинок. Сколько груш было у Незнайки?

№7. Ваня разложил камешки на столе на расстоянии 2 см один от другого. Сколько камешков разложил он на протяжении 10 см? Напиши ответ.

№8. Во дворе находятся куры и поросята. Всего 5 голов и 14 ног. Сколько во дворе кур и сколько поросят? Напиши ответ.

№9. Сто орехов разложили на пять nачек. В первой и во второй в сумме -51 орех, во второй и третьей – 44, в третьей и четвертой -31, а в четвертой, 5- 33. Найди количество орехов в каждой кучке. Напиши ответ.

№10. Бочонок, полный меда, весил 12 кг. Когда половину меда съели, бочонок стал весить 7 кг. Напиши, сколько он будет весить, когда весь мед съедят?

№11. Вдоль беговой дорожки расставлены столбы. Старт дан у первого столба. Через 12 минут бегун был у четвертого столба. Через сколько минут от начала старта бегун будет у седьмого столба? (скорость бегуна постоянная)

№12. Вова и Дима решали задачу за 10 минут. Сколько времени потратил на решение задачи каждый мальчик?

№13. У Данилы в двух карманах 20 рублей. Когда из одного кармана в другой он переложил 6 рублей, то в обоих карманах денег стало поровну. Сколько денег (в рублях) было первоначально в каждом кармане?

№14. Ручка дороже карандаша на 15 рублей. На сколько рублей 5 ручек стоят дороже 5 карандашей?

№15.Длина бревна 5 метров. В одну минуту от бревна отпиливают по одному метру, За сколько минут распилят все бревно?

№ 16. Аня, Боря, Вера и Гена – лучшие лыжники школы. Для участия в соревнованиях надо составить команду из трех лыжников. Сколькими способами можно составить такую команду?

№17. Гусь весит 2 кг. Сколько он будет весить, если встанет на одну ногу?

№18. У Миши несколько солдатиков, а у Саши их в два раза больше. Вместе у мальчиков 9 солдатиков. Сколько солдатиков у каждого мальчика?

№19. На дереве сидели три птички. К ним прилетели еще две птички. Кот подкрался и схватил одну птичку. Сколько птичек осталось на ветке?

№20. Трое играли в шашки. Всего сыграли 3 партии. Сколько партий сыграл каждый, если все сыграли поровну?

Ответы: (№ 1- 50 к; № 2- поровну; № 3- 7 шт.яиц; № 4- 20 с; № 5- 2 р; № 6-10; № 7- 6 к; № 8- 3 кур. 2 пор; № 9- в первой-33, во второй- 28, в третьей- 16, в четвертой-15, в пятой- 18; №10-2 кг. №11 – через 24 минуты; №12.- 10 минут; №13 – 16 и 4 рубля; №14 -75 рублей; №15- за 4 мин; №16- 4 способа; №17- 2 кг; №18- у Миши -3, у Саши -6; №19- ни одной; №20

Задания для

4 класса

с ответами

1. Катя, Вера и Рита нарисовали 3 цветка: василёк, ромашку, гвоздику. Какой цветок нарисовала каждая девочка, если Рита не рисовала василёк, Вера не рисовала ромашку и василёк?

2. Близнецов зовут Иван Петрович и Василий Петрович. Их отцу столько же лет, сколько обоим близнецам вместе. А его отцу Николаю Денисовичу столько же лет, сколько обоим близнецам и их отцу. Как зовут отца близнецов и сколько им лет, если Николаю Денисовичу 80 лет?

3. Вадим, Сергей и Михаил изучают различные иностранные языки: китайский, японский, арабский. На вопрос, какой язык изучает каждый из них, один ответил: «Вадим изучает китайский, Сергей не изучает китайский, а Михаил не изучает арабский». Впоследствии выяснилось, что в этом ответе только одно утверждение верное, а два других – ложные. Какой язык изучает каждый из молодых людей?

4. Бревно длиной 12 метров распилили на 6 равных частей. Сколько распилов сделали?

5. Коля, Петя и Ваня собирали грибы. Коля нашёл 10 сыроежек и столько белых, сколько подберёзовиков нашёл Ваня. Ваня нашёл лисичек в 2 раза меньше, чем сыроежек Коля, и 3 подберёзовика. Петя нашёл только лисички, которых у него больше, чем белых у Коли, но меньше, чем лисичек у Вани. Сколько грибов собрали ребята, если известно, что Коля нашёл только сыроежки и белые грибы, а Ваня – подберёзовики и лисички?

6. Фамилии Веры и Оли – Гордеева и Светлова. Какую фамилию имеет каждая девочка, если известно, что Вера и Гордеева одноклассницы?

7. Три сестры учились в разных классах одной школы: Таня, Катя и Лариса. Таня была старше Кати, а Катя старше Ларисы. Кто старше: Таня или Лариса?

8. Каждая из трёх подруг – Катя, Алиса и Аня – получили от Деда Мороза игрушки: медвежонка, зайчонка, слоника. Известно, что Катя не получала зайчика. Аня не получала ни слоника, ни медведя. Кто какую игрушку получил?

9. Три одноклассницы – Соня, Таня и Женя – занимаются в различных спортивных секциях. Одна из них – в гимнастической, другая – в лыжной, третья занимается плаванием. Каким видом спорта занимается каждая из них, если известно, что Соня плаваньем не увлекается, Таня в лыжную секцию никогда не ходила, а Женя является победителем в соревнованиях по лыжам?

10. Ира, Надя, Варя и Лена вышивали. Три девочки вышивали пейзаж, одна – натюрморт. Ира и Надя вышивали разные картины, Ира и Лена тоже разные. Что вышивала Ира?

11. У Кости в ведре ерши, пескари, окуни – всего 14 рыбок. Ершей на 10 больше, чем пескарей. Сколько ершей, пескарей и окуней в отдельности у мальчика?

12. Митя, Сеня Тима, Юля и Катя пришли в музей до его открытия и встали в очередь. Если бы Митя встал посередине очереди, то он стоял бы между Сеней и Катей, а если бы Митя встал в конце очереди, то рядом с ним стояла бы Юля. Но Митя встал впереди своих товарищей. Кто за кем стоит?

13. Имеются двое песочных часов на 3 минуты и 7 минут. Надо опустить яйцо в кипящую воду ровно на 4 минуты. Как это сделать с помощью данных часов?

14. Как с помощью 5-литровой кастрюли и 3-литровой банки налить из водопроводного крана в ведро ровно 4 л воды?

15. Группа туристов состоит из 6 иностранцев. Они говорят по-французски и по-английски. 4 человека говорят по-английски, 3 по-французски. Сколько человек говорят только на одном языку, а сколько – на двух?

16. Ваня съел на два пончика больше Кати и на два пончика меньше Оли. Вместе они съели 12 пончиков. Сколько пончиков съел каждый?

17. В магазине было 6 разных ящиков с гвоздями. Масса ящиков 6, 7, 8, 9, 10 и 11 кг. Два покупателя приобрели 5 ящиков. Причём каждому гвоздей досталось одинаково. Какой ящик остался в магазине?

18. Масса поросенка и пса 64 кг, барана и пса – тоже 64 кг, а пса и барана – 60 кг. Какова масса поросёнка?

19. Лестница состоит из 9 ступенек. На какую ступеньку надо встать. Чтобы оказаться на середине лестницы?

20. Маша и Петя встретились в вагоне электропоезда. Маша всегда садится в 5-й вагон от начала поезда, а Петя – в 5-й вагон от конца поезда. Сколько вагонов в поезде?

21. Вдоль одной стороны огорода надо поставить изгородь. Длина огорода 10 м. Сколько потребуется столбов. Чтобы поставить их по длине огорода на расстоянии 2 м друг от друга?

22. Три одинаковые ватрушки надо разделить поровну между 4 детьми. Как это сделать, выполнив наименьшее число разрезов?

23. Ширина занавески для окна 1м 20 см. Надо пришить 6 колец на одинаковом расстоянии друг от друга (первое и последнее кольца должны располагаться по краям занавески). Сколько сантиметров надо оставлять между кольцами?

24. Вдоль беговой дорожки через одинаковое расстояние выкопали столбы. Старт дан у первого столба. Через 12 минут бегун был у 4-го столба. Через сколько минут от начала старта бегун будет у 7-го столба, если он бежит с одинаковой скоростью?

25. Верёвку разрезали на 2 части так, что одна часть оказалась в 4 раза длиннее другой. Чему равна длина верёвки, если одна часть длиннее другой на 18 см?

26. Одного фермера спросили, сколько у него денег. Он ответил: «Мой брат втрое богаче меня, отец втрое богаче брата, дед втрое богаче отца, а всех у нас ровно 100 000 рублей. Узнайте, сколько у меня денег?»

27. Трое ребят были на рыбалке. Вместе они поймали 14 рыб. Андрей поймал рыбы меньше всех. Дима поймал в 3 раза больше рыб. Чем Вова. Сколько рыб поймал каждый мальчик?

28. По вертикальному столбу высотой 6 м движется улитка. За день она поднимается на 4 м, за ночь опускается на 3м. Сколько дней ей потребуется, чтобы добраться до вершины?

29. Катя, Соня, Галя, Тамара родились 2 марта, 17 мая, 2 июня,20 марта. Соня и Галя родились в одном месяце, а у Гали и Кати дни рождения обозначались одинаковыми числами. Кто какого числа и в каком месяце родился?

30. Трое ребят играли в шашки. Всего сыграли 3 партии. Сколько партий сыграл каждый мальчик?

РЕШЕНИЯ ЛОГИЧЕСКИХ ЗАДАЧ (3-4кл.)

1. Табличный способ решения:

Имя девочки	Василёк	Ромашка	Гвоздика
Катя	+	-	-
Вера	-	-	+
Рита	-	+	-

2. Способ рассуждения: Близнецы Петровичи, значит. Их отца зовут Пётр. Он сын Николая Денисовича, значит, он Николаевич. Его возраст вместе с возрастом близнецов равен возрасту Николая Денисовича, то есть 80 годам. А так как его возраст равен возрасту обоих близнецов, то он равен 40 годам, а возраст обоих близнецов равен 4о годам. Но близнецы имеют одинаковый возраст. Значит, каждому из них 20 лет.

ОТВЕТ: Пётр Николаевич; 20 лет.

3. Способ логического рассуждения:

Имеются три утверждения:

1) Вадим изучает китайский.

2) Сергей не изучает китайский.

3) Михаил не изучает арабский.

Если первое утверждение верное, то верное и второе, т.к. юноши изучают разные языки. Это противоречит условию задачи, поэтому первое утверждение – ложное.

Если второе утверждение верное, то первое и третье должны быть ложными. При этом получается, что никто не изучает китайский язык. Это противоречит условию, поэтому второе утверждение тоже ложное.

Остаётся считать верным третье утверждение. А первое и второе – ложными. Следовательно, Вадим не изучает китайский,китайский изучает Сергей. Михаил – японский, Вадим – арабский.

4. Решение. Строим чертёж___!___!___!___!___!___

ОТВЕТ: 5 распилов.

5. Способ доказательного умозаключения.

Так как Коля нашёл 10 сыроежек, а Ваня – в 2 раза меньше лисичек, то Ваня нашёл 5 лисичек. Ваня нашёл 3 подберёзовика, а Коля – столько же белых. Тогда число лисичек, найденных Петей, больше 3, но меньше 5, так что Петя нашёл 4 лисички. Отсюда следует, что всего собрали 25 грибов. ( 10+3+3+5+4=25)

6. ОТВЕТ: Вера Светлова и Оля Гордеева

7. ОТВЕТ: Таня (чертеж).

8. Таблица

Имя девочки	Медведь	Зайчик	Слоник
Катя	+	-	-
Алиса	-	+
Аня	-	-	+

9. Таблица:

Имя девочек	Гимнастика	Лыжи	Плаванье
Соня	+	-	-
Таня	-	-	+
Женя	-	+	-

10. ОТВЕТ: Ира вышивала натюрморт (рассуждение).

11. ОТВЕТ: 11 ершей, 1 пескарь, 2 окуня (подбором)

12. ОТВЕТ: Митя Тима Сеня Катя Юля ( Чертёж)

13. ОТВЕТ: Следует поставить часы для работы

одновременно. Когда песок в 3-минутных часах истечёт, положить яйцо в кипящую воду. Оставшееся время работы 7-минутных часов ровно 4 минуты. (рассуждение)

14. ОТВЕТ: 2 раза трёхлитровой банкой наполняем кастрюлю доверху, тогда в банке остается 1 л воды, её выливаем в ведро. Добавляем в ведро ещё 3 литра воды.

15. ОТВЕТ: Только по-английски говорят 3 человека, только по-французски 2 человека, на двух языках говорит 1 человек. ( с помощью диаграммы Венна) или

4-3=1(чел.) – на двух языках; 4-1=3(чел.) – только на английском; 3-1=2(чел.) – только на французском

16. ОТВЕТ: 2, 4, 6 пончиков (подбором)

Сколько съели бы дети, если бы Веня съел столько, сколько Коля? 12-2=10

На сколько Оля съела больше Коли? 2+2=4

Сколько съели бы дети, если бы и Оля , и Ваня съели каждый столько, сколько Коля? 10-4=6

Сколько съел Коля? 6:3=2

17. ОТВЕТ: Первый покупатель приобрёл ящики в 6кг, 7кг, 8кг, второй приобрёл ящики в 10кг и 11кг. Т есть каждый купил по 21кг гвоздей. Значит, остался ящик с 9кг гвоздей.

18. ОТВЕТ: Поросёнок весит 34 кг (рассуждение).

19. ОТВЕТ: На пятую ступеньку (рассуждение, рисунок).

20. ОТВЕТ: 9 вагонов. (чертёж).

21. ОТВЕТ: 6 столбов (чертёж).

22. ОТВЕТ: 2 ватрушки разрезать пополам, а третью – на 4 части. (рисунок).

23. ОТВЕТ: 120 : 5 = 24 см (чертёж).

24. ОТВЕТ: через 24 минуты (чертёж).

25. ОТВЕТ: 30см (схема)

26. ОТВЕТ: 2500 рублей. (схема или уравнение).

27. ОТВЕТ: Вова поймал 3 рыбы, Дима – 9 рыб, Андрей – 2 рыбы. (подбором).

28. ОТВЕТ: К концу 3 дня (чертёж).

29. ОТВЕТ: Галя -2марта, Соня – 20 марта, Катя – 2 июня, Тамара – 17 мая. (рассуждение, таблица)

30. ОТВЕТ: 2 партии ( схема-граф)

ОЛИМПИАДНЫЕ ЗАДАНИЯ 3-4 КЛАССЫ

3 класс

Выполните действия: 424 + 18 + 455 + 76 + 45 + 982 + 17. Укажите самый простой порядок выполнения действий.

Ответ: (424 + 76) + (18 + 982) + (455 + 45) + 17 = 2017 (порядок действий может быть и другой).

Обучающиеся агроботанической смены Центра “Стратегия” решили посадить на опытном участке три грядки клубники. На первой грядке они высадили 15 кустов клубники, а на каждой следующей грядке было на 5 кустов больше, чем на предшествующей. Сколько всего кустов клубники было посажено на трёх грядках?

Решение. 1. 15 + 5 = 20 кустов  на второй грядке. 2. 20 + 5 = 25 кустов  на третьей грядке. 3. 15 + 20 + 25 = 60 кустов  всего. Ответ: 60 кустов.

Когда в Калининграде 8 часов, в Липецке – 9 часов. Когда в Липецке 10 часов, в Якутске – 16. Какое время в Калининграде, когда в Якутске 12 часов? Решение. 9 – 8 + 16 – 10 = 7 часов – разница во времени между Калининградом и Якутском. Ответ: 5 часов.

Малыш и Карлсон разлили 4 литра варенья по двум банкам и понесли домой. Малыш устал и перелил 2 литра варенья из своей банки в банку Карлсона. От этого у Малыша варенья стало втрое меньше, чем у Карлсона. Сколько варенья стало у Карлсона? Решение. У Малыша варенья стало втрое меньше, чем у Карлсона. Значит, у Малыша осталась четвертая часть от всего варенья, т.е. 1 литр, а у Карлсона всё остальное: 3 литра. Ответ: 3 литра.

Фермер построил загон шестиугольной формы и разделил его на равные треугольники со стороной 1 м (как показано на рисунке). В некоторых треугольниках он решил посадить капусту, а в некоторые запустил коз. Теперь предприимчивому фермеру интересно, какой минимальной общей длины нужно построить забор по сторонам треугольников, чтобы ни одна коза не могла добраться до капусты. Определите длину полученного забора и объясните, как он расположен. Минимальность длины забора можно не доказывать.

Решение. Есть и другие способы построения забора длиной 7 м, забор меньшей длины построить нельзя. Ответ: 7 м.

Вася и Петя любят кольца. Однако Петя любит соединенные кольца, а Вася нет. Помогите Васе определить, какое минимальное количество колец надо разрезать, чтобы все три кольца, изображенные на рисунке, отделились друг от друга? Решение. Кольцо 3 находится над кольцом 2, поэтому, если разрезать кольцо 1, то все кольца отделятся друг от друга. Аналогично можно разрезать кольцо 3. Ответ: 1.
К Одинокой горе пришли всего 18 хоббитов и гномов. Во время похода каждый гном познакомился с 4 хоббитами, а каждый хоббит – с 5 гномами. Сколько всего в отряде было гномов и сколько хоббитов? (Пояснение: знакомство всегда взаимно.) Решение. Из условия задачи ясно, что хоббитов меньше, чем гномов, и их количества относятся, соответственно, как 4 : 5. Отсюда очевидно, что если всего персонажей 18, то хоббитов 2 ∙ 4 = 8, а гномов 2 ∙ 5 = 10. Ответ: 10 гномов и 8 хоббитов.
На круговом шоссе расположено 7 городов. Уникум обнаружил, что в каком бы городе он не оказался, до одного из двух ближайших по часовой стрелке городов он может доехать за 40 минут на велосипеде, а до другого, также по часовой стрелке,  за 20 минут на мопеде. И на мопеде, и на велосипеде Уникум движется с постоянной скоростью без остановок, причем на мопеде быстрее. За сколько минут Уникум сможет проехать один круг по всему шоссе на мопеде? Решение. 1. Пусть x, y м/мин – скорости, соответственно, велосипеда и мопеда. Назовем города, расположенные на круговом шоссе, как A, B, C, D, E, F, G (по часовой стрелке в указанном порядке). 2. По условию задачи расстояния между любыми парами соседних городов равны. Если расстояние между двумя соседними городами (например, B и C, C и D) равно 20y м, а городами B и D равно 40x м, то скорости велосипеда и мопеда равны, что не соответствует условию задачи. 3. Следовательно, расстояние между любыми двумя соседними городами (например, B и C, C и D) равно 40x м, а городами A и C, B и D, C и E равно 20y м. Так как расстояния между любыми парами соседних городов равны, то Уникум проезжает расстояние между соседними городами за 10 мин, а один круг на шоссе за – 70 мин. Ответ: 70 минут.
Обучающиеся детского технопарка “Кванториум” решили отправиться в лодочный поход. Если ребят посадить по четыре человека в лодку, то останется две незанятых лодки. Если же рассадить по три человека, то все лодки окажутся занятыми и еще пять человек останутся без места. Определите, сколько обучающихся решили отправиться в лодочный поход и сколько было лодок. Решение. 1. 4  2 + 5 = 13 человек – разность между количеством обучающихся в случае, когда в каждой лодке сидело по четыре человека, и случаем когда в каждой лодке сидело по три человека. Полученная разность равняется количеству лодок. 2. 4  (13  2) = 44  обучающихся решили отправиться в лодочный поход. Ответ: 44 обучающихся, 13 лодок.
Незнайка решил потренировать свои вычислительные навыки. Он написал на доске число 2017 и решил каждый день, за исключением выходных, прибавлять к числу, записанному на доске, или вычитать из него номер дня в неделе (в понедельник прибавляется или вычитается 1, во вторник  2, в среду  3, в четверг  4, в пятницу  5). После выполнения действия на доске записывается новое число, а старое стирается. Ровно через 7 недель Незнайка увидел, что на доске опять записано число 2017, не ошибся ли Незнайка в своих вычислениях? Знайка, который все 7 недель наблюдал за вычислениями Незнайки, утверждает, что должно было получиться число 2018. Могло ли в результате описанных вычислений получиться число 2018? Решение. 1. Каждую неделю Незнайка прибавляет к числу, записанному на доске, или вычитает из него поочередно числа 1, 2, 3, 4, 5. Среди указанных чисел три нечетных, поэтому через неделю на доске будет записано число другой четности. Исходное число было нечетным, следовательно, через нечетное число недель (через 7 недель) на доске будет записано четное число. Незнайка ошибся в вычислениях. 2. Для получения числа 2018, например, достаточно вы полнить следующие действия. Первые три недели числа только добавляются, следующие три недели числа только вычитаются. Тогда после 6 недель на доске будет опять записано число 2017. Действия в последнюю неделю 2017 + 1 + 2  3  4 + 5 = 2018. Возможны и другие способы получения числа 2018. Ответ: Незнайка ошибся в вычислениях, а число 2018 получиться могло.

класс

Выполните действия: 125 258 4 2017 . Укажите самый простой порядок выполнения действий. Решение. 125 258 411 (1258)(4 25) 2017  201 700 000 (порядок действий может быть и другой). Ответ: 201 700 000.
В 8 одинаковых бутылках 16 литров кваса (бутылки полностью наполнены). Сколько потребуется таких бутылок, чтобы разлить 24 литра кваса? Решение. 1. 16 : 8 = 2 литра  вместимость одной бутылки. 2. 24 : 2 = 12 бутылок  потребуется для 24 литров кваса. Для задачи можно составить выражение: 24 : (16 : 8). Ответ: 12 бутылок.
На столе лежат 17 монет. По крайней мере, одна из них двухрублевая. Какие бы две монеты не взять, хотя бы одна из них будет достоинством 5 рублей. Какая сумма лежит на столе? Решение. Если взять двухрублевую монету и любую другую, одна из них будет пятирублевой. Значит любая монета за исключением двухрублевой монеты – пятирублевая. И на столе лежит 5 ∙ 16 + 2 = 82 рубля. Ответ: 82 руб. 4. Малыш и Карлсон разлили 6 литров варенья по двум банкам и понесли домой. Малыш устал и перелил 2 литра варенья из своей банки в банку Карлсона. От этого у Малыша варенья стало вдвое меньше, чем у Карлсона. Сколько варенья было у Карлсона первоначально? Решение. У Малыша варенья стало вдвое меньше, чем у Карлсона. Значит, у Малыша осталась третья часть от всего варенья, т.е. 2 литра, а у Карлсона все остальное: 4 литра. Тогда первоначально у Карлсона было 2 литра варенья. Ответ: 2 литра.
Группа из 23 школьников стали делить грибы, которые они собрали в лесу, между собой. Если они разделят грибы из двух лукошек поровну (по количеству), то останется один лишний гриб. Если разделят грибы из трех лукошек поровну, то останется 13 лишних грибов. Определите, какое наименьшее количество грибов может быть в одном таком лукошке. Количество грибов во всех лукошках было одинаково. Решение. 1. Разность количества грибов, которые школьники поделили между собой, во втором и первом случаях должна делиться на 23. Эта разность равна количеству грибов в одном лукошке минус 12 грибов (если разность отрицательна и кратна 23, то число грибов в лукошке должно быть отрицательно, что невозможно). Наименьшее неотрицательное число, делящееся на 23, равно 0. Поэтому минимальное число грибов в лукошке 12. 2. Число 12 удовлетворяет условию задачи. Ответ: 12.
Вася и Петя любят кольца. Однако Петя любит соединенные кольца, а Вася нет. Помогите Васе определить, какое минимальное количество колец надо разрезать, чтобы все пять колец отделились друг от друга? Решение. 1. Кольцо 3 находится над кольцом 2, поэтому, если разрезать кольцо 1, то кольца 1, 2, 3, и 5 отделятся друг от друга. Для разделения колец 3 и 4 достаточно разрезать одно из них. 2. Меньше двух разрезов недостататочно, так как кольца 1 и 5, а также кольца 3 и 4 соединены между собой. Один разрез может убрать только одно из указанных соединений. Возможен выбор и других пар разрезаемых колец. Ответ: 2.
У Гендальфа есть необычная доска для игры в шахматы, она меньшего размера, чем обычно: 5 на 5. Сколькими способами можно заштриховать на этой доске одну или несколько клеток, чтобы они образовывали различные по расположению или размеру квадраты? Гендальфу удалось получить 32 таких квадрата, удастся ли Вам улучшить его результат? Решение. 1. 25 квадратов – из одной клетки. 2. 16 квадратов – из четырех клеток. Левой верхней клеткой выбранного квадрата, в этом случае может являться любая клетка квадрата 4 на 4.
9 квадратов – из девяти клеток. Левой верхней клеткой выбранного квадрата, в этом случае может являться любая клетка квадрата 3 на 3. 4. 4 квадрата – из 16 клеток. Левой верхней клеткой выбранного квадрата, в этом случае может являться любая клетка квадрата 2 на 2. 5. 1 квадрат (весь исходный квадрат) – из 25 клеток. 6. 25 + 16 + 9 + 4 + 1 = 55. Ответ: 55.
В трактире городка Бри близ Шира посетители на вечер выбирают роли лжецов и правдолюбов. Первые всегда говорят неправду, вторые всегда правдивы. Торин присел за столик с тремя местными жителями и спросил у каждого: “Сколько среди двух твоих друзей правдолюбов?” На что получил следующие ответы. Первый: “Ни одного”. Второй: “Один”. Что сказал третий? Решение. Предположим, что первый сказал правду. Тогда оба его соседа лгут. 1 2 3 П Л Л Но в этом случае второй сказал правду – противоречие. Значит, первый солгал. Предположим, что второй солгал. 1 2 3 Л Л Л Тогда третий должен также быть лжецом. Но в этом случае слова первого оказались правдивы, снова противоречие. Значит, второй сказал правду. 1 2 3 Л П П Но тогда и третий должен говорить правду. Тогда он скажет «один». Ответ: один.
Хоббиты Фили и Кили смотрят на аквариум и наблюдают за траекторией рыбки, перерисовывая ее себе на пергамент. Причем они смотрят на соседние стенки аквариума. Фили изобразил траекторию справа (на рисунке), Кили – слева (на рисунке). Какую траекторию изобразил бы Радагаст, который наблюдал за рыбкой сверху? Ответ:
Уникум знакомился с делением отрезка на части. Вначале он отметил на отрезке точки, делящие его на 15 равных частей. Затем он стер отмеченные точки и на том же отрезке нарисовал точки, делящие его на 25 равных частей. Далее он опять стер отмеченные точки и на том же отрезке нарисовал точки, делящие его на 35 равных частей. Затем Уникум задумался, на сколько частей удалось разделить отрезок, если бы точки не стирались? Помогите Уникуму решить эту задачу. Решение. Точек первого вида 14, второго – 24, третьего – 34. Причем точки, делящие отрезок на 5 частей, отмечались в каждом из трех случаев, так как 35 7 25 5 15 3 5 1    , 35 14 25 10 15 6 5 2    , 35 21 25 15 15 9 5 3    , 35 28 25 20 15 12 5 4    . Таким образом, на отрезке было отмечено 14 + 24 + 34 – 4 ∙ 2 = 64 различные точки. 64 различные точки делят отрезок на 65 частей. Ответ: 65.