Мастер – класс
Приготовила учитель математики МБОУ(К)Ш №60,Разработал урок учитель Гааг Клавдия Алексеевна.

Цель:
Цель мастер-класса: выявление теоретических и методических основ привития познавательного интереса в процессе учебной деятельности и решения заданий, имеющих несколько решений, способствующих формированию познавательного интереса при обучении математике, развитию творческого потенциала личности учащегося.
Класс делится на группы ,в каждой группе-лидер. Учитель предлагает по одному участнику из группы выйти к столу на котором лежат шарфы и повязать шарф так, чтобы у всех был завязан по разному.---Замечательно—просто класс! Применим это на задачах—решим одну задачу несколькими способами.
Для лучшего усвоения учащимися решения задач разных видов используется «Урок одной задачи».
Урок одной задачи – это поиск разных способов решения задач разных видов.
На этом уроке ученик может узнать различные приемы решения задач, у него появляется шанс найти свой способ решения, который понятен ему. Услышать разные рассуждения, мнения. Таким образом, он учиться думать, отстаивать свое мнение, находить выход из сложившейся ситуации.
В целях совершенствования преподавания математики целесообразно использовать такие уроки раз в четверть. Я использую этот метод при проведении консультаций, при подготовке к ЕГЭ или ГИА.
Решение задач различными способами требует применения комплекса ранее полученных знаний. Поэтому это процесс систематизации усвоенных учащимися знаний и умений. Этот метод помогает восполнить пробелы в ранее изученных темах, побуждает к поиску различных приемов решения задач. К тому же формирует умение исследовать, анализировать прочитанное, правильно оформлять свои записи, развивает гибкость ума и критическое мышление.
Решение задач различными способами – это увлекательный творческий процесс, развивающий воображение.
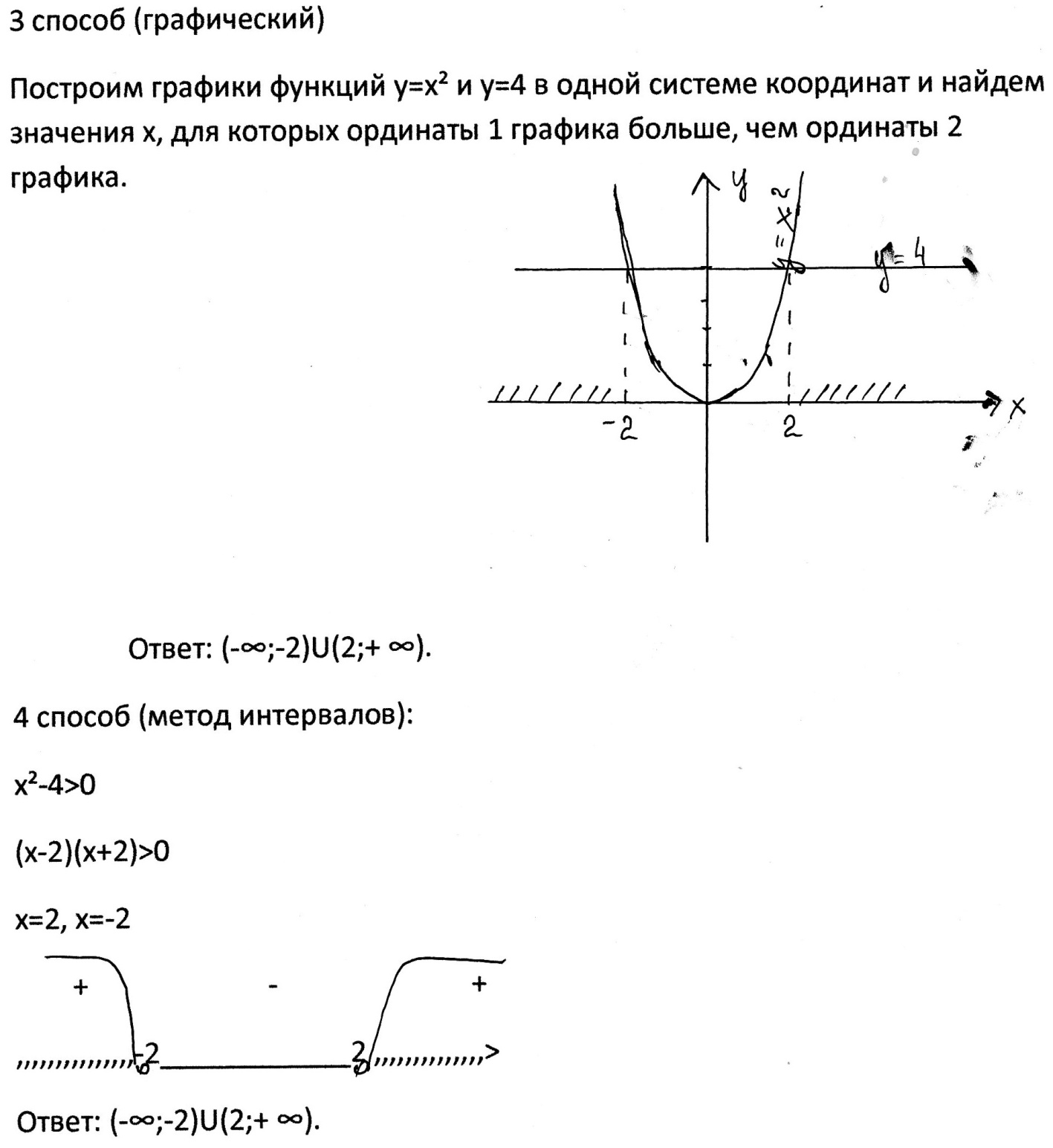
Решить неравенства
Предлагаю вам попробовать решить задачи, которые вам предложены, разными способами.
Задача на арифметическую прогрессию
Найти сумму первых 12-и членов арифметической прогрессии, если её четвертый член равен 3, а шестой равен -1,2.
Решение: чтобы найти сумму первых 12-и членов, надо найти а₁ и d арифметической прогрессии.
1 способ:{а₄=а₁+3d, = ˃{3=a₁+3d , =˃{ a₁=3-3d, =˃{a₁=3-3(-2,1),
{a₆=а₁+5d; {-1,2= а₁+5d; {-1,2=3-3d+5d; {d=-2,1;
=˃{а₁=9,3
{d=-2,1. S=-27.
2 способ: а₆=а₄+2d=3+2d
-1,2=3+2d
d=-2,1, а₄=а₁+3d=˃ a₁=a₄-3d=3-3(-2,1)=9,3 Sn=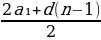
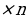 , S₁₂=-27
, S₁₂=-27
3 способ: Используем свойство арифметической прогрессии
an = (an + 1 + an – 1 )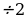 - среднее арифметическое
- среднее арифметическое
а₅=(а₄+а₆)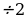 =0,9
=0,9
d=a₅-a₄=0,9-3=-2,1
а₁=а₄-3d=9,3 Sn=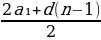
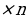 S₁₂=-27.
S₁₂=-27.
Геометрическая задача
В равностороннем треугольнике АВС сторона которого равна 6см, найти высоту треугольника.
Дано:
∆АВС
АВ=ВС=АС=6 см
Найти: ВD 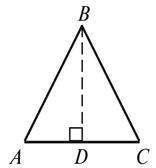
1 способ: по определению sin‹A: sin60=ВD AB, где ‹А=‹В=‹С=60,
AB, где ‹А=‹В=‹С=60,
√3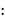 2=BD
2=BD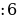 , BD=3√3см.
, BD=3√3см.
2 способ: по теореме Пифагора
∆АВD, ‹D=90, АВ=6, ‹А=60, тогда ‹АВD=30, АD=АВ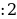 =3 см
=3 см
ВD²=АВ² - АD²=36-9=27, BD=3√3см.
3 способ: по теореме синусов
∆АВD, ‹D=90 ВD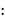 sin‹A=AB
sin‹A=AB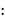 sin‹D
sin‹D
ВD=6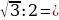 3√3см.
3√3см.
4 способ: по теореме косинусов
ВD²=АВ² +АD²-2АВ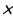 АD
АD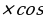 60=36+9-18=27, BD=3√3см.
60=36+9-18=27, BD=3√3см.

Рефлексия
Как вы думаете, для математического развития учащихся полезнее решить одну задачу несколькими способами или несколько однотипных задач одним способом?
Какие качества по вашему мнению, вырабатываются у школьника при отыскании различных способов решения задач?
Хочу отметить, что работа учителя – это постоянный поиск и творчество, поэтому каждый выбирает свои методы, пользуется своими индивидуальными приемами.
«Хороших методов существует ровно столько, сколько существует хороших учителей» (Д. Пойа)
Общие методы решения задач должны стать прочным достоянием учащихся, но наряду с этим необходимо воспитывать у них умение использовать индивидуальные особенности каждой задачи, позволяющие решить её проще. Отход от шаблона и конкретный анализ условий задачи являются залогом её успешного решения.
2







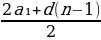
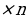 , S₁₂=-27
, S₁₂=-27 - среднее арифметическое
- среднее арифметическое
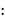 AB, где ‹А=‹В=‹С=60,
AB, где ‹А=‹В=‹С=60,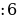 , BD=3√3см.
, BD=3√3см.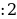 =3 см
=3 см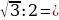 3√3см.
3√3см.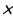 АD
АD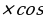 60=36+9-18=27, BD=3√3см.
60=36+9-18=27, BD=3√3см.











