Математическая модель "Производная"

Классная работа

«Производная

и её применение»

«Знание только тогда знание, когда оно приобретено усилиями своей мысли, а не памятью».  (Л.Н.Толстой )

«.. нет ни одной области в математике, как бы абстрактна она ни была , которая когда-либо не окажется применимой к явлениям действительного мира…»

1. Что называется производной функции в точке?

2. В чем заключается геометрический смысл производной?

3. В чем заключается механический смысл производной?

4. В чём заключается достаточный признак возрастания функции?

5. В чём заключается достаточный признак убывания функции?

6. Какие точки называют критическими точками функции?

7. Назовите необходимое условие экстремума.

8. Назовите признак максимума функции.

9. Назовите признак минимума функции.

Разминка

Найти производную функции

ответы

1

f(x)

а

f(x)= х ⁵+2х-6

б

3

5х+2

2

f(x)=(3х-4)²

5х ⁵ +2

в

6(3х-4)

f(x)=sin4x

4

-12(3х-4)

cos4x

г

5х  +2

f(x)= 6+cos²x

-cos4x

х  +2

2(3х-4)

2sinx

5

3(3х-4)

4cos4x

f(x)=7x+π

- 2sinx

4sin4x

7x

6+2cosx

7

-2cosxsinx

π

7+π

ответы

f(x)

1

f(x)= х ⁵+2х-6

а

2

f(x)=(3х-4)²

б

3

в

f(x)=sin4x

+

4

г

+

f(x)= 6+cos²x

5

+

f(x)=7x+π

+

+

Исаак Ньютон

Готфрид Лейбниц

Жозеф Лагранж

x

d x

f ’

«В мире не происходит ничего, в чем бы не был виден смысл какого-нибудь максимума или минимума». Леонард Эйлер.

Признак возрастания и убывания функции

=

y

По характеру изменения графика функции укажите, на каких промежутках производная положительна, на каких отрицательна. Каждая из функций определена на R

1

x

0

1

-1

2

на

на

Ответ:

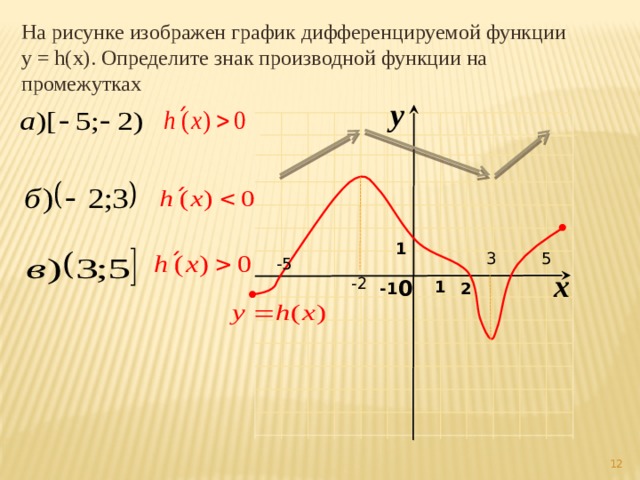
На рисунке изображен график дифференцируемой функции y = h(x). Определите знак производной функции на промежутках

y

1

5

3

-5

x

-2

0

1

-1

2

11

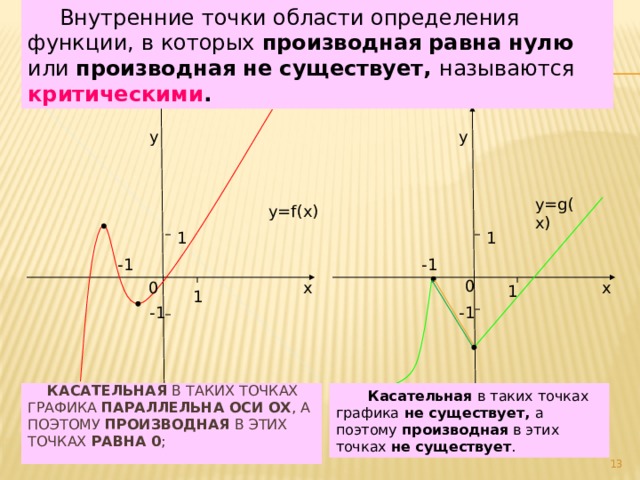
Внутренние точки области определения функции, в которых производная равна нулю или производная не существует, называются критическими .

у

у

y=g(x)

y=f(x)

1

1

-1

-1

0

0

х

х

1

1

-1

-1

Касательная в таких точках графика не существует, а поэтому производная в этих точках не существует .

Касательная в таких точках графика параллельна оси ОХ , а поэтому производная в этих точках равна 0 ;

12

плавные линии

угловатые линии

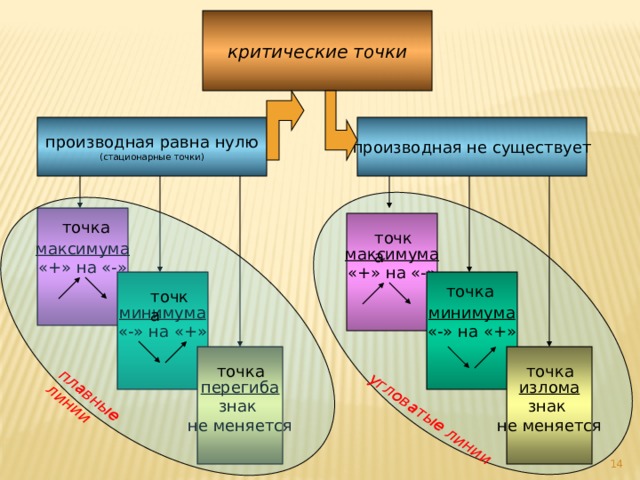
критические точки

производная равна нулю

производная не существует

(стационарные точки)

максимума

«+» на «-»

максимума

точка

«+» на «-»

точка

минимума

минимума

«-» на «+»

«-» на «+»

точка

точка

излома

перегиба

знак

знак

не меняется

не меняется

точка

точка

12

Достаточное условие существования экстремума функции :

• Если при переходе через критическую точку х 0 функции f(x) ее производная меняет знак с «+» на «-», то х 0 – точка максимума функции f(x).

• Если при переходе через критическую точку х 0 функции f(x) ее производная меняет знак с «-» на «+», то х 0 – точка минимума функции f(x).

3) Если при переходе через критическую точку х 0 функции f(x) ее производная не меняет знака, то в точке х 0 экстремума нет.

12

Тест 2 Cвязь свойств функций и производной.

1 вариант

монотонно

у'= -5

возрастает

имеет максимум во внутренней точке

у'=2-х

имеет минимум во внутренней точке

у'= 1+2х

постоянна

у'= 0

монотонно убывает

у'= 5

2 вариант

у'= 0

монотонно

у'=-1,5

имеет максимум во внутренней точке

возрастает

имеет минимум во внутренней точке

у'= -0,5х

постоянна

у'= х-2

у'= 1,5

монотонно убывает

взаимопроверка

1 вариант

у'= - 5

монотонно

возрастает

имеет максимум во внутренней точке

у'=2-х

имеет минимум во внутренней точке

у'= 1+2х

постоянна

у'= 0

монотонно убывает

+

+

у'= 5

+

+

+

2 вариант

у'= 0

монотонно

у'=-1,5

имеет максимум во внутренней точке

возрастает

имеет минимум во внутренней точке

у'= -0,5х

постоянна

у'= х-2

+

у'= 1,5

монотонно убывает

+

+

+

+

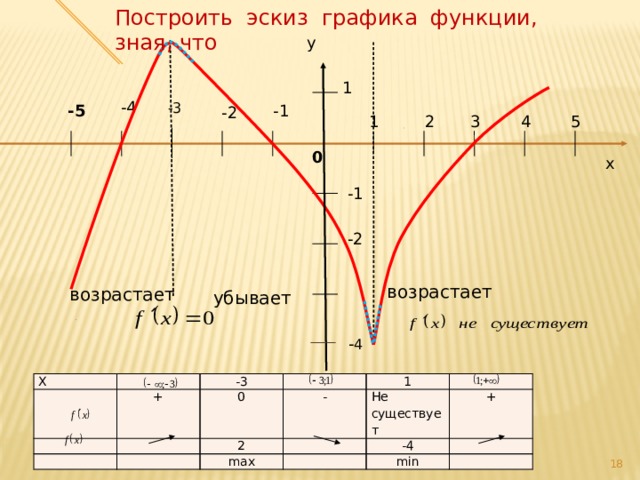
Построить эскиз графика функции, зная, что

y

1

-4

-3

-5

-1

-2

1

2

4

5

3

0

x

-1

-2

возрастает

возрастает

убывает

- 4

X

-3

+

0

2

-

1

Не существует

max

-4

+

min

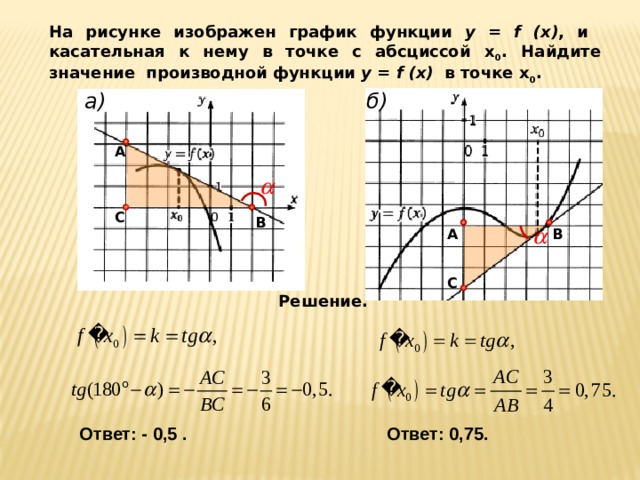
На рисунке изображен график функции y = f (x) , и касательная к нему в точке с абсциссой х 0 . Найдите значение производной функции y = f (x) в точке х 0 .

б)

a)

А

С

В

В

А

С

Решение.

Ответ: 0,75.

Ответ: - 0,5 .

Задача 8 (2) На рисунке изображен график производной функции f (x) , определенной на интервале (—7; 5). Найдите точку экстремума функции f (x ) на отрезке [-6; 4].

-3

+

-

-6

4

Решение.

Отметим на рисунке границы отрезка, о котором идет речь в условии задачи.

На этом отрезке производная функции один раз обращается в 0 (в точке -3) и при переходе через эту точку меняет знак, откуда ясно, что точка -3 и есть искомая точка экстремума функции на отрезке.

Ответ: -3.

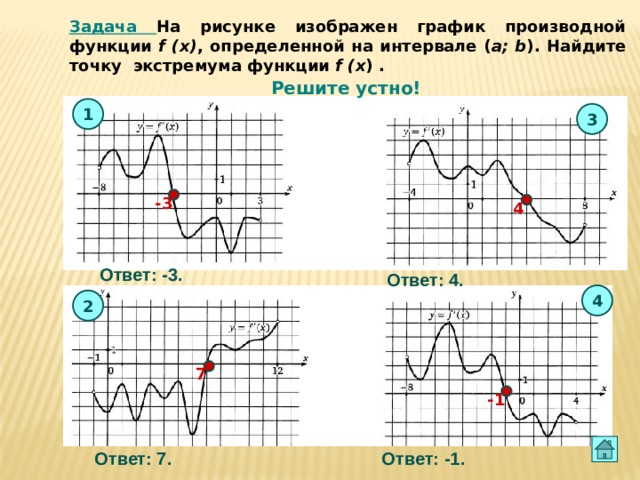
Задача На рисунке изображен график производной функции f (x) , определенной на интервале ( a; b ). Найдите точку экстремума функции f (x ) .

Решите устно!

1

3

-3

4

Ответ: -3.

Ответ: 4.

4

2

7

-1

Ответ: -1.

Ответ: 7.

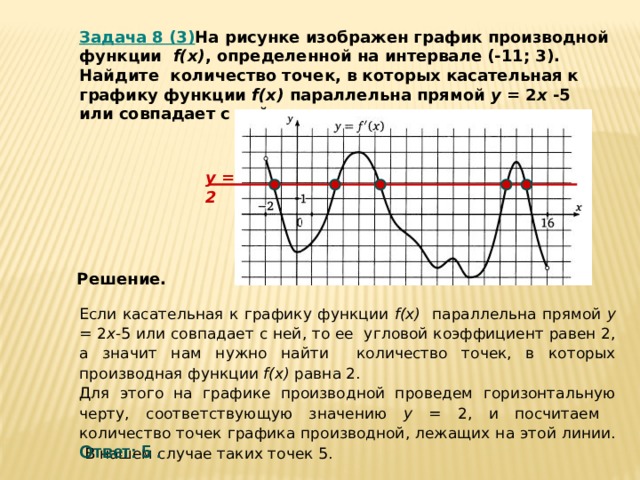
Задача 8 (3) На рисунке изображен график производной функции f(x) , определенной на интервале (-11; 3). Найдите количество точек, в которых касательная к графику функции f(x) параллельна прямой y = 2 x -5 или совпадает с ней.

y = 2

Решение.

Если касательная к графику функции f(x) параллельна прямой y = 2 x -5 или совпадает с ней, то ее угловой коэффициент равен 2, а значит нам нужно найти количество точек, в которых производная функции f(x) равна 2.

Для этого на графике производной проведем горизонтальную черту, соответствующую значению y = 2, и посчитаем количество точек графика производной, лежащих на этой линии. В нашем случае таких точек 5.

Ответ: 5 .

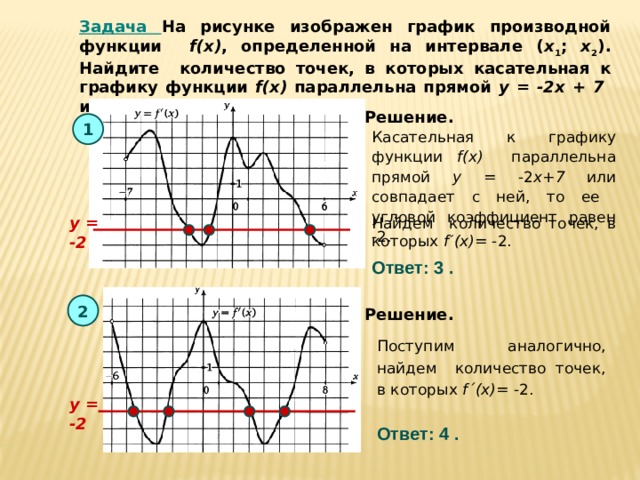
Задача На рисунке изображен график производной функции f(x) , определенной на интервале ( x 1 ; x 2 ). Найдите количество точек, в которых касательная к графику функции f(x) параллельна прямой y = -2x + 7 или совпадает с ней.

Решение.

1

Касательная к графику функции f(x) параллельна прямой y = -2 x+7 или совпадает с ней, то ее угловой коэффициент равен -2.

y = -2

Найдем количество точек, в которых f ´ (x) = -2.

Ответ: 3 .

2

Решение.

Поступим аналогично, найдем количество точек, в которых f´(x) = -2.

y = -2

Ответ: 4 .

График функции и график производной

Установите соответствие между графиками функций и графиками производных

1 вариант

2 вариант

РЕФЛЕКСИЯ

Анализ своей работы

1.Вам все на уроке

было понятно и со всеми заданиями вы справились

2.Вам все на уроке

было понятно, но не со всеми заданиями вы справились

3. На уроке было много

непонятного и с всеми заданиями вы не справились

Домашнее задание

• Заполните кроссворд
• Исследовать функцию у=0,2(х³+4х² -11х -30)

" Мысли в фокус"(клетки с числами не заполнять)

1. Угол ее наклона выражает геометрический смысл производной.

2. Великий немецкий ученый, философ, математик, физик, юрист, языковед,создатель математического анализа, основоположник большой математической школы.

3. Раздел физики, помогающий понять смысл производной.

4. Точка интриганка, точка

5."Microsoft Windows в переводе на русский "Компания…"

6. Имя английского физика и математика, автора сочинения "Математические начала натуральной философии"

7. Маленькая, серенькая на коврике лежит. Что это?

8. Утверждение, которое в ходе исследовательской работы подтверждается или опровергается.

9. Синоним понятию "дифференциальное исчисление"

10. Производная- это….

11. Внешний носитель информации в компьютере.

12. Устройство вывода информации в компьютере.

13. Одна из эффективных форм проверки знаний учащихся.

14. "Любите … - источник знаний".

15. Соответствие, при котором каждому числу х из множества D сопоставляется по некоторому правилу число y, зависящее от х.

14

1

15

6

8

9

5

12

4

10

11

13

3

2

7