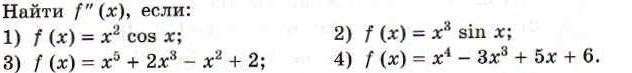Математика группа 1-10 на 22.04

Предмет: математика

Дата проведения: 22.04.2020г.

Группа: 1-10 Преподаватель: Касымова У.Ш

Литература: А.Ш.Алимов

Цель: повторить понятие производной функции, ее физический смысл, основные формулы дифференцирования;

ввести понятие первообразной функции, научить учащихся определять является ли функция F(x) первообразной для функции f(x).

Развивающие: развивать у учащихся грамотную устную и письменную математическую речь, научное мировоззрение.

Воспитательные: воспитывать умение участвовать в диалоге, понимать точку зрения собеседника, признавать право на иное мнение.

Тема: определение первообразной

Ход урока:

1.орг.момент

2.новая тема

     Прежде чем знакомиться с понятием первообразной, давайте в самых общих чертах вспомним самую обычную производную. Не углубляясь в занудную теорию пределов, приращений аргумента и прочего, можно сказать, что нахождение производной (или дифференцирование) – это просто математическая операция над функцией. И всё. Берётся любая функция (допустим, f(x) = x²) и по определённым правилам преобразовывается, превращаясь в новую функцию. И вот эта самая новая функция и называется производной.

        В нашем случае, до дифференцирования была функция f(x) = x², а после дифференцирования стала уже другая функция f’(x) = 2x.

        Производная – потому, что наша новая функция f’(x) = 2x произошла от функции f(x) = x². В результате операции дифференцирования. И причём именно от неё, а не от какой-то другой функции (x³, например).

        Математики – народ неугомонный. На каждое своё действие стремятся найти противодействие. :) Есть сложение – есть и вычитание. Есть умножение – есть и деление. Возведение в степень – извлечение корня. Синус – арксинус. Точно также есть дифференцирование – значит, есть и… интегрирование.)

        А теперь поставим такую интересную задачу. Есть у нас, допустим, такая простенькая функция f(x) = 1. И нам надо ответить на такой вопрос:

        Производная КАКОЙ функции даёт нам функцию f(x) = 1?

Так от какой же исходной функции (назовём её F(x)) произошла наша производная функция f(x) = 1? Или, в математической форме, для какой функции F(x) выполняется равенство: 

        F’(x) = f(x) = 1?

      F(x) так, чтобы равенство сработало. :) Ну как, подобрали? Да, конечно! F(x) = x. Потому, что:

        F’(x) = x’ = 1 = f(x).

        Разумеется, найденную мамочку F(x) = x надо как-то назвать, да.) Знакомьтесь!

        Первообразной для функции f(x) называется такая функция F(x), производная которой равна f(x), т.е. для которой справедливо равенство F’(x) = f(x).

        Вот и всё. Больше никаких научных хитростей. В строгом определении добавляется ещё дополнительная фраза "на промежутке Х". Но мы пока в эти тонкости углубляться не будем, ибо наша первоочередная задача – научиться находить эти самые первообразные.

        В нашем случае как раз и получается, что функция F(x) = x является первообразной для функции f(x) = 1.

        Почему? Потому что F’(x) = f(x) = 1. Производная икса есть единица. Возражений нет.)

        Термин "первообразная" по-обывательски означает "родоначальница", "родитель", "предок". Сразу же вспоминаем самого родного и близкого человека.) А сам поиск первообразной – это восстановление исходной функции по известной её производной. Иными словами, это действие, обратное дифференцированию. И всё! Сам же этот увлекательный процесс тоже называется вполне научно – интегрирование. Но об интегралах – позже. Терпение, друзья!)

        Запоминаем: 

        Интегрирование — это математическая операция над функцией (как и дифференцирование).

        Интегрирование — операция, обратная дифференцированию.

        Первообразная — результат интегрирования.

     А теперь усложним задачу. Найдём теперь первообразную для функции f(x) = x. То есть, найдём такую функцию F(x), чтобы её производная равнялась бы иксу:

        F’(x) = x

        Кто дружит с производными, тому, возможно, на ум придёт что-то типа:

        (x²)’ = 2x.

     Что ж, респект и уважуха тем, кто помнит таблицу производных!) Верно. Но есть одна проблемка. Наша исходная функция f(x) = x, а (x²)’ = 2x. Два икс. А у нас после дифференцирования должен получиться просто икс. Не катит. Но…

       Мы ведь хотим, чтобы справа остался чистый икс, верно? А двойка мешает… Вот и берём соотношение для производной (x²)’ = 2x и делим обе его части на эту самую двойку:

  Полученное равенство как раз и означает, что искомой первообразной для функции f(x) = x служит функция F(x) = x²/2.

3.закрепление

4. домашнее задание

Показать, что функция F(x) является первообразной

для функции f(х):

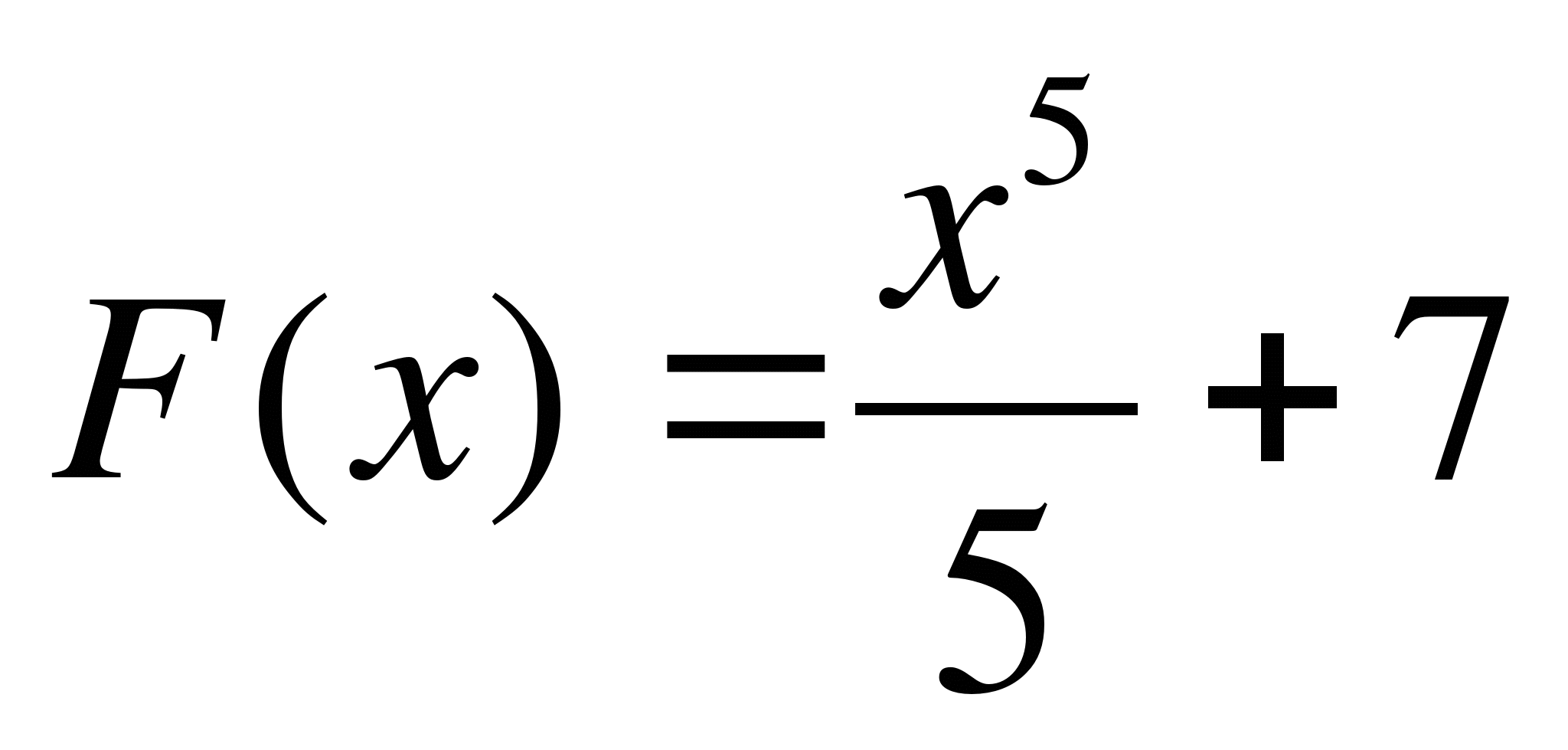
1 )

2)   1) F(x) = x³-2x+1     f(x)=3x²-2

   3) F(x)= x⁴-7           f(x)=4x³

^{5.итог урока} Ответы присылайте на почту:

[email protected]

Укажите дату, ФИО и группу

 Предмет: математика

Дата проведения: 23.04.2020г.

Группа: 1-10 Преподаватель: Касымова У.Ш

Литература: А.В. Погорелов

Цель: ввести понятие о свойствах первообразной

Тема: основные свойства первообразной

Ход урока.

1.орг. момент

2. новая тема

Основное свойство первообразной

Будет справедлива следующая теорема. Теорема: любая первообразная для некоторой функции f на промежутке А может быть записана в виде:

F(x) +C, где F(x) – одна из первообразных для данной функции f на промежутке A, а С – некоторая произвольная постоянная.

Теорема, приведенная выше, называется еще основным свойством первообразной. Разберем её более подробно, так как в ней скрывается целых два свойства первообразной функции.

1. При подстановке любого числа вместо С в эту формулу получим первообразную функции f на промежутке А.

2. Если взять любую первообразную Ф для функции f на некотором промежутке А. То для этой производной можно подобрать некоторое число С, такое что для любого х будет выполняться следующее равенство: Ф(х) = F(x)+C.

Это свойство можно очень наглядно интерпретировать. Графики первообразных одной и той же функции будут получаться один из другого параллельным переносом вдоль оси Оу. И таких графиков будет бесконечно много.

Рассмотрим следующий пример: найти общий вид первообразных, для функции f(x) = -x^3 на всей числовой оси.

Одной из первообразных будет являться функция –(x^4)/4, так как (–(x^4)/4)’ = -x^3. Следовательно, по теореме об основном свойстве первообразной, представленной выше, общий вид первообразных для функции f = -x^3 будет следующий:

F(x) = –(x^4)/4 + C.

При нахождении первообразных функции f промежуток, на котором задана функция f, обычно не указывают - для краткости записи. При этом, всегда имеются ввиду такие промежутки, чтобы они были как можно большей длины. 

3.закрепление

1). Найти общий вид первообразных для функций f:

а) f (х)=5; б) f (х)=х⁴; в) f (х)=; г) f (х)=4; д) f (х)=3

е) f (х)= 1; ж) f (х)=3х³-5х²; з) f (х)=; и) f (х)=+1

;

2) . Найти первообразную функции: 2х + 1.

А) х(х+1)+с; В) х²+1+с; С) х(х-1)+с; Д) х²+2х+с.

3) Вместо точек поставьте какую — нибудь функцию, удовлетворяющую равенству:

а) (….)´= 7х;  б)(....)´= cosx;     в)(....)´= -  1  ;   г)(....)´=       1    ;    

                                                                     х²                        2√х                    

4. домашнее задание

1. а)найдите первообразную данной функции F(x) =4х³

б)найдите первообразную данной функции F(x) = 5x⁴-3

в) найдите первообразную данной функции F(x) = 6x⁵-4

2. найти производную функции f= х²+2х+9

5. Итог урока

Ответы присылайте на почту:
[email protected]

Укажите дату, ФИО и группу

Предмет: математика

Дата проведения: 24.04.2020г.

Группа: 1-10 Преподаватель: Касымова У.Ш

Литература: А.Ш.Алимов

Цель: закрепить понятие о первообразной и решение примеров

Тема: определение первообразной

Ход урока:

1. Фронтальный опрос:

1.Что называется производной

2. Как называется процесс нахождения производной;

3. Назовите основные формулы дифференцирования:

а)Чему равна производная степенной функции. Назовите производную функции х⁸, х^-9,

.

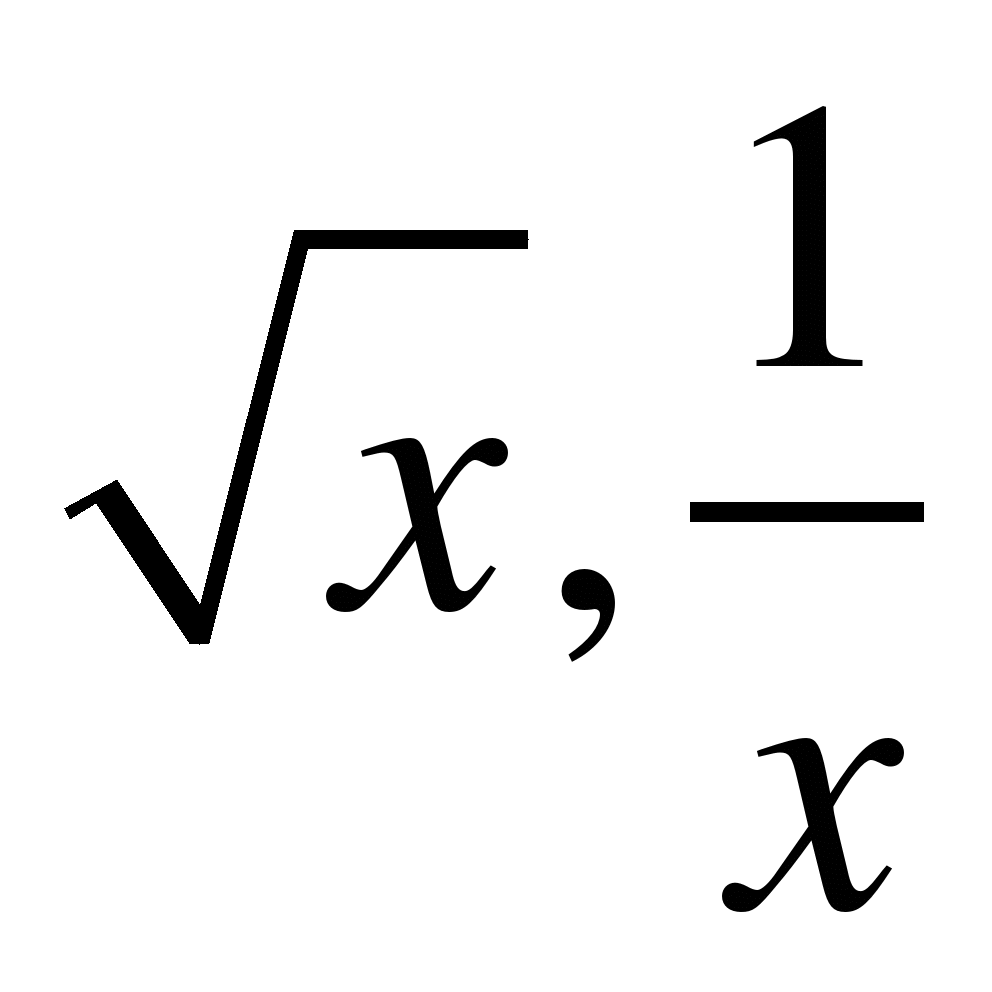б) производные тригонометрических функций;

в) производная сложной функции.

4. Сформулируйте правила вычисления производных.

3. Проверочная работа с выбором ответа (с самопроверкой) (выполняется на листочках)

Найти производную функции

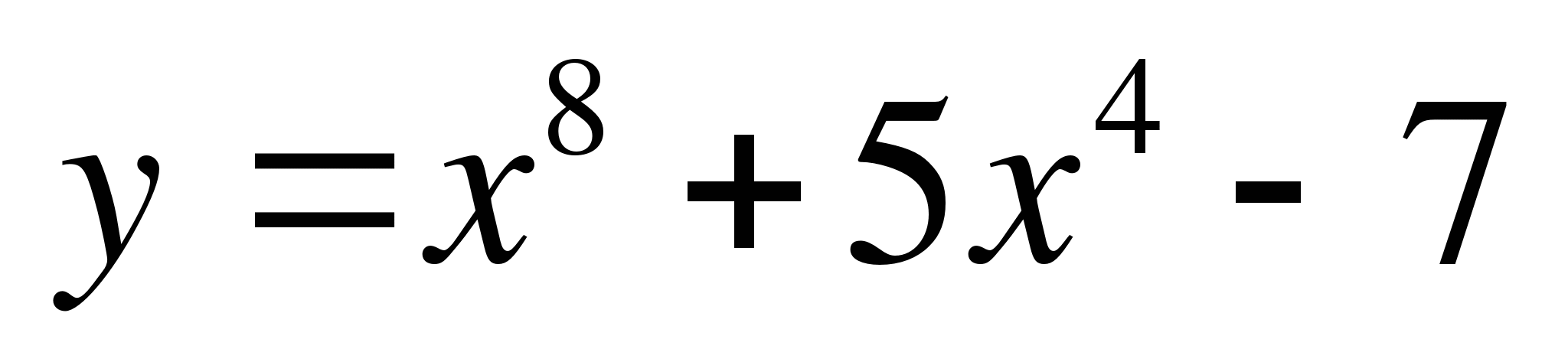
1.

Варианты ответов:

а)

б)

в)

2. y=tg x-3x

Варианты ответов

а )

б )

в )

3.

Варианты ответов:

а)

б)

в)

4 .

Варианты ответов:

а)

б )

в )

5. Найти первообразную для функции f(x):

    1) f(x)= x³ 

    2) f(x) = x²

      3) f(x) = x

6. Домашнее задание

1.Вычислить производные следующих функций:

(1)^/ =                         (х³)^/=                  

(х)^/ =                          

(30х)^/=                       ( 5х¹⁰)^/=

2.заполнить пропущенные места в скобках

                   (…)^/ = 2х                         (…)^/ = 0

                   (…)^/ = 4х³                       (…)^/ = 25

7. итог урока

Ответы присылайте на почту:
[email protected]

Укажите дату, ФИО и группу