Предмет: математика
Дата проведения: 15.04.2020г.
Группа: 1-7 Преподаватель: Касымова У.Ш
Литература: А.В. Погорелов
Цель: ввести понятие о координатах
Тема: Координаты и векторы в пространстве
Ход урока:
Отрезком обозначают ограниченный двумя точками участок прямой. Точки – концы отрезка.
Общеизвестный факт, что каждая точка А плоскости имеет свои координаты (х, у).
Даны А и В — точки плоскости с координатами (х1y1) и (х2,у2).
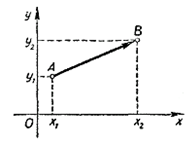
В данном примере вектор AB задан координатами (х2— х1, y2— y1). Квадрат длины вектора будет равен сумме квадратов его координат. Следовательно, расстояние d между точками А и В, или, что то же самое, длина вектора АВ, вычисляется согласно формуле:
d2= (х2— х1)2+ (y2— y1)2.
Извлекая квадратный корень из выражения, находим:

Эта формула длины отрезка предоставляет возможность рассчитывать расстояние между двумя произвольными точками плоскости, при условии, что известны координаты этих точек
Вышеуказанную формулу длины отрезка можно доказать и другим способом. В системе координат заданы координаты крайних точек отрезка координатами его концов(х1y1) и (х2,у2).
Прочертим прямые лини через эти точки перпендикулярно к осям координат, в результате имеем прямоугольный треугольник. Первоначальный отрезок является гипотенузой образовавшегося треугольника. Катеты треугольника сформированы отрезками, их длиной будет проекция гипотенузы на оси координат.
Установим длину этих проекций.
На ось у длина проекции равна y2 - y1, а на ось х длина проекции равна х2 - х1. На основании теоремы Пифагора видим, что |AB|² = (y2 – y1)² + (x2 – x1)².
В рассмотренном случае |AB| выступает длиной отрезка.
Вычислим длину отрезка АВ, для этого извлечем квадратный корень. Результатом является все та же формула длины отрезков по известным координатам конца и начала.
Дано:  и
и  . Найти длину отрезка
. Найти длину отрезка  .
.
Решение: по соответствующей формуле:

Ответ: 
Определение.
Середина отрезка - это точка, которая лежит на отрезке и находится на равном расстоянии от конечных точек.
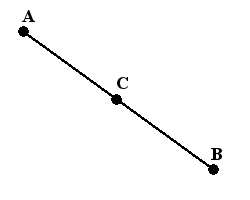
В геометрических задачах часто можно столкнуться с необходимостью найти середину отрезка заданного координатами точек его концов, например в задачах поиска медианы, средней линии, ...
Каждая координата середины отрезка равна полусумме соответствующих координат концов отрезка.
Формулы вычисления расстояния между двумя точками:
Формула вычисления координат середины отрезка с концами A(xa, ya) и B(xb, yb) на плоскости:
| xc = | xa + xb | | yc = | ya + yb |
| 2 | 2 |
Формула вычисления координат середины отрезка с концами A(xa, ya, za) и B(xb, yb, zb) в пространстве:
| xc = | xa + xb | | yc = | ya + yb | | zc = | za + zb |
| 2 | 2 | 2 |
Примеры задач на вычисление середины отрезка
Примеры вычисления координат середины отрезка на плоскости
Пример 1.
Найти координаты точки С, середины отрезка AB заданного точками A(-1, 3) и B(6, 5).
Решение.
| xc = | xa + xb | = | -1 + 6 | = | 5 | = 2.5 |
| 2 | 2 | 2 |
| yc = | ya + yb | = | 3 + 5 | = | 8 | = 4 |
| 2 | 2 | 2 |
Ответ: С(2.5, 4).
Задание №1 Дано: А(1;-4) и В(-2;6)
Найти:
Задание№2 Дано: А(2;-5;3) и В(-2;-3;5)
Найти:
Задание№2 Дано: А(1;-3;4) и В(-3;2;7)
Найти:
Домашнее задание
1) А(3;-6) и (-1;7)
Найти:
Итог урока Ответы присылайте на почту:
[email protected]
Укажите дату, ФИО и группу
Предмет: математика
Дата проведения:16.04.2020г.
Группа: 1-7 Преподаватель: Касымова У.Ш
Литература: А.В. Погорелов
Цель: ввести понятие о координатах
Тема: Декартовы координаты и векторы в пространстве
Ход урока:
Чтобы найти координаты вектора  , если заданы координаты его начала и конца, необходимо от координат конца отнять соответствующие координаты начала. В случае если точки заданы на плоскости и имеют соответственно координаты
, если заданы координаты его начала и конца, необходимо от координат конца отнять соответствующие координаты начала. В случае если точки заданы на плоскости и имеют соответственно координаты  и
и  , то координаты вектора
, то координаты вектора  вычисляются по формуле:
вычисляются по формуле:

Если точки заданы в пространстве и имеют координаты  и
и  соответственно, то координаты вектора
соответственно, то координаты вектора  вычисляются по следующей формуле:
вычисляются по следующей формуле:
Примеры нахождения координат вектора
Пример
Задание. Даны точки  и
и  . Найти координаты векторов
. Найти координаты векторов  и
и 
Решение. Точки заданны на плоскости, поэтому координаты вектора  вычислим по формуле:
вычислим по формуле:

Подставляя координаты заданных точек, получим:

Для нахождения вектора  исходная формула примет вид:
исходная формула примет вид:

то есть

Ответ. 
Пример
Задание. Даны точки  ,
,  и
и  . Найти координаты вектора
. Найти координаты вектора  ,
,  .
.
Решение. Точки заданны в пространстве, поэтому для нахождения координат искомых векторов будем пользоваться формулой

Подставляя заданные координаты, получим:
Для вектора  имеем:
имеем:
Ответ.
Задача № 1 Найти координаты вектора АВ, если А(-3;3;12)и В(5;-2;-4)
Решение:
Чтобы найти сумму векторов  , которые заданны координатами
, которые заданны координатами  и
и  , необходимо сложить соответствующие координаты этих векторов, то есть
, необходимо сложить соответствующие координаты этих векторов, то есть
В случае если векторы заданы в пространстве, то есть  и
и  , то их сумма равна
, то их сумма равна
Примеры нахождения суммы векторов
Пример
Задание. Найти сумму векторов  ,
,  и
и 
Решение. Для нахождения суммы векторов, сложим их соответствующие координаты
Ответ. 
Пример
Задание. Найти суммы векторов  ,
,  ,
,  и
и  , если
, если  ,
,  и
и 
Решение. Для нахождения искомой суммы векторов сложим их соответствующие координаты:
Ответ.  ,
,  ,
,  ,
, 
Задача № 2 найти сумму векторов а(-3; -5;-4) и b(-6; -4; -10)
Решение:
Задача № 3 Найдите сумму векторов: а) АВ и АС б) PR и PS в) AB,BD,CD и DA
Решение: А) АВ + АС=ВС; б) PR + PS=RS; в) AB+BD+CD+DA=AD+CD=AC+DA=CD
4 этап: домашнее задание
1 Найти координаты вектора АВ, если А(-3;7;1)и В(-1;2;5)
найти сумму векторов а(3; --2;-4) и b(-4; -2; 10)
5 этап: итог урока Ответы присылайте на почту:
[email protected]
Укажите дату, ФИО и группу
Предмет: математика
Дата проведения: 17.04.2020г.
Группа: 1-7 Преподаватель: Касымова У.Ш
Литература: А.В. Погорелов
Тема: Контрольная работа
Цель: проанализировать результаты усвоения тем; умения решать задачи; способность формированию навыков самоконтроля, самостоятельности.
Ход урока
1.Орг.момент
2. выполнение заданий
Что называется вектором?
а)Найти координаты вектора АВ, если А(-4;0;1)и В(3;2;0)
в)Найти координаты вектора АВ, если А(5;1;-6)и В(-7;0;2)
Что называется координатами вектора?
что называется суммой векторов?
найти сумму векторов а(3; --1;-2) и b(5; -4; 0)
найти длину вектора АВ, если А(-4;2) и В(1;-3)
что такое середина отрезка?
а)Найти координаты середины отрезка АВ, если А(-3;6) и В9(7;4)
в) Найти координаты середины отрезка АВ, если А(-7;3) и В(5;-9)
Итог урока: оценивание
Ответы присылайте на почту:
[email protected]
Укажите дату, ФИО и группу


















